不同泊松比蜂窝夹芯结构的抗爆性能对比分析

宫晓博， 刘宇鸿， 于昌利

(哈尔滨工业大学(威海) 海洋工程学院，山东 威海 264209)

蜂窝夹芯结构有轻质量、高比刚度、高比强度的特点，是一种优良的吸能结构，所以经常被应用在舰船和车辆的爆炸防护结构上。蜂窝夹芯结构经过长期的发展，出现了许多形状各异的蜂窝，如内凹六边形、星形和双箭头形等[1]。由于拓扑结构的不同，蜂窝结构具有不同的泊松比，可以分为正泊松比[2]、零泊松比[3]和负泊松比[4]3大类。

蜂窝夹芯结构优异的抗冲击能力吸引众多工程技术人员的研究。Ruan等[5]通过数值模拟和实验，研究了正六边形蜂窝在不同冲击方向的面内变形模式和失效机理，并且验证了数值模型的合理性；Zhu等[6]固定了蜂窝结构的壁厚参数，通过计算和实验研究了六边形蜂窝的壁厚、边长和材料弹性模量对结构静态性能的影响；Jin等[7]通过数值模拟方法研究了负泊松比蜂窝夹芯结构在爆炸荷载作用下的抗爆性能，并且详细研究了其变形机理以及不同爆炸距离和不同的胞元排列方式下结构的动态响应；乔锦秀[8]计算推导了双箭头形蜂窝结构的面内力学特性，用数值模拟方法验证了推导的正确性，并且研究了结构的吸能特性；高松林[9]对星形蜂窝结构的力学特性进行了多方面的计算和探讨，重点研究了星形蜂窝结构在局部冲击载荷作用下的抗冲击性能；姚兆楠[10]研究了负泊松比蜂窝材料与正六边形蜂窝材料的面内冲击结果，进而将2种蜂窝材料的动力学特性进行了对比；Gong等[11]提出了一种新型二维四角星零泊松比蜂窝夹芯结构，并研究了该蜂窝的静力学特性；Zhang等[12]通过数值模拟，详细讨论了壁厚、芯层-壁厚比、泊松比和爆破类型等因素对蜂窝夹芯结构动态响应的影响，研究表明，在动荷载作用下，负泊松比蜂窝结构比正泊松比的更为优异；Liu等[13]对比研究了蜂窝结构在不同泊松比(-3.3～3.3)情况下的抗冲击性能。

现有的研究工作大都针对单一蜂窝夹芯结构，综合分析蜂窝壁厚、臂长和角度等几何参数对其静态力学性能和动态力学性能的影响，尚无不同泊松比蜂窝夹芯结构的抗爆性能的对比分析。分析过程中所用的蜂窝结构的等效相对密度和等效弹性模量等参数不一致，无法充分探讨泊松比对蜂窝结构抗爆性能的影响。基于此，本文以5种不同类型蜂窝为研究对象，通过调整蜂窝胞元的壁厚和臂长，使不同类型的蜂窝芯材具有相同的等效相对密度和等效弹性模量，以研究泊松比对蜂窝夹芯结构抗爆性能的影响。在相同环境的水下爆炸数值模拟中，对比分析了不同泊松比蜂窝结构抗爆性能的优劣。

1 蜂窝结构抗爆性能数值模拟模型

水下爆炸是一个极短时间内的能量转换过程，一般发生在水下的极小体积内或面积上。当炸药在水中爆炸时，装药和介质的界面处的爆炸产物以极快的速度向四周扩散，形成初始冲击波[14]。若载荷很大，则造成的高压甚至会使材料发生可压缩流动，这种情况下结构的动态响应极为复杂，想要建立精确的力学模型来描述其变形是很困难的，只能通过简化的近似模型进行预测[15]。鉴于水下爆炸冲击实验的成本要求高，本文使用LS-DYNA进行数值模拟，数值模拟方法能很大程度上弥补成本过高的缺陷。

1.1 数值模拟计算模型建立

采用Rhino建立了5种常用的蜂窝结构模型，包括双箭头形、星形、内凹六边形、四角星形和正六边形蜂窝，并利用LS-DYNA软件模拟了水下爆炸冲击过程，水下抗爆模型以图1为例，其他类型蜂窝不再赘述。

图1 正六边形蜂窝夹芯结构水下爆炸模型

蜂窝夹芯结构由2层厚度为2 mm的板和不同壁厚的蜂窝芯层组成，材料均采用45#钢。蜂窝夹芯结构为四边简支约束，胞元层数为3层，通过调整蜂窝胞元的臂长和壁厚等参数，使5种蜂窝的等效相对密度均约为0.1，等效弹性模量均约为300 MPa，表1给出5种蜂窝结构实际计算的等效相对密度和等效弹性模量，胞元尺寸参数如表2和图2所示。

表1 5种蜂窝胞元的等效相对密度和等效弹性模量

表2 5种蜂窝胞元的尺寸参数

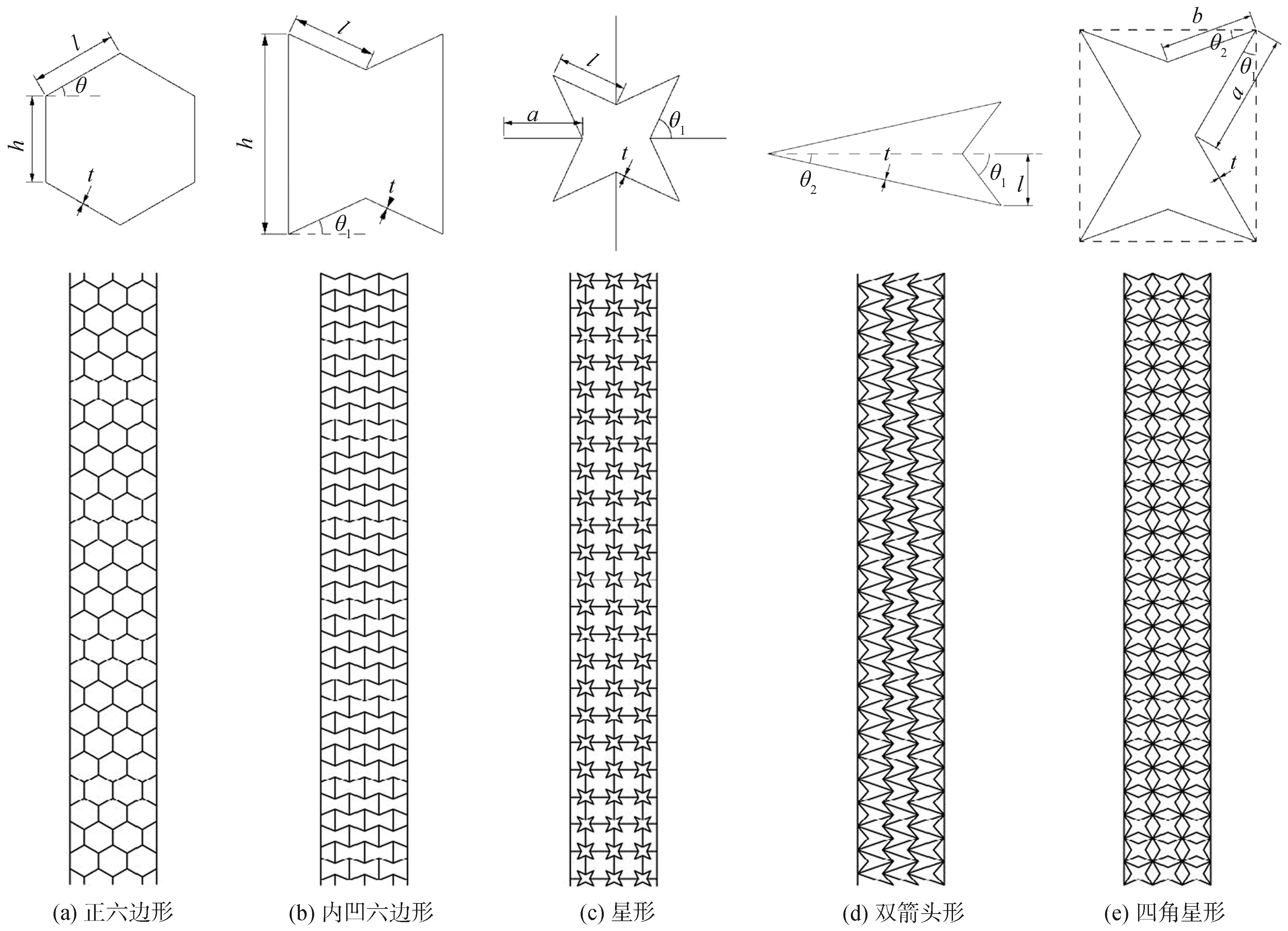
图2 5种蜂窝夹芯结构

实验采用三硝基甲苯炸药，水下爆炸计算模型中炸药与蜂窝结构距离50 mm，炸药当量为100 g。计算模型包括水、空气、炸药和蜂窝夹芯结构，模型均采用4节点shell单元，背板、面板和蜂窝结构的网格尺寸为10 mm，仿真时间为3 ms。

1.2 流体环境、炸药与结构材料参数

1.2.1 流体环境参数

水介质采用空材料模型，在LS-DYNA中，使用关键字MAT_NULL和Gruneisen进行定义。其中Gruneisen方程为：

(γ0+αμ)E0

(1)

式中：p为压力；μ为泊松比；ρ=1 g/cm3；C=1 484 m/s；S1=1.979；S2=S3=0；γ0=0.11；α=3；V0=1；初始内能E0=307.2 kPa。

空气同样采用空材料模型，使用关键字Linear Polynomial进行定义，Linear Polynomial方程为：

p=C0+C1μ+C2μ2+C3μ3+

(C4+C5μ+C6μ2)E0

(2)

式中：ρ=0.001 28 g/cm3；C4=C5=0.4；C1=C2=C3=C6=0；初始内能E0=250 kPa。

1.2.2 炸药参数

采用关键字MAT_HIGH_WXPLOSIVE_BURN描述炸药特征，炸药采用JWL状态方程为：

(3)

式中：ρ=1.62 g/cm3；V=6 898 m/s；A=371.2 GPa；B=3.23 GPa；R1=4.15；R2=0.95；w=0.30；E0=9.6 GPa；V0=1。

1.2.3 结构材料参数

蜂窝夹芯结构材料采用45#钢。在爆炸过程中，爆炸反应会产生应变较大和应变率较高的现象，且在爆炸过程中往往涉及高温变形的情况，所以计算采用Johnson-Cook本构模型。该塑性模型考虑了应变率和绝热(忽略热传导)温度，材料的屈服强度可表示为：

(4)

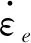
为熔点；Tr为室温；CV为比热。

破坏应变定义为：

(5)

式中：σ*为压力与有效压力之比；ρ=7.82 g/cm3；E=200 GPa；υ=0.3；Tm=1 783 K；Tr=293 K；本构模型常数A=0.507 GPa；B=0.32 GPa；C=0.064；n=0.28，m=1.06；失效模型常数D1=0.1；D2=0.76；D3=1.57；D4=0.005；D5=-0.84。D1～D5为断裂常量，当破坏参数D达到1时即认为发生断裂：

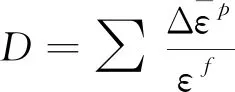
(6)

LS-DYNA中，水、空气与蜂窝夹芯结构间的流固耦合用关键字CONSTRAINED_LAGRANGE_IN_SOLOD进行定义，采用任意拉格朗日-欧拉方法(ALE算法)进行计算。ALE算法即空气、水和炸药用多物质ALE描述，将Lagrange描述的蜂窝夹芯结构包围起来，二者通过设置耦合来进行相互作用[17]，该方法使网格在整个分析过程中保持一种比较良好的状态，不会出现巨大的扭曲与变形。

1.3 水下爆炸ALE数值方法验证

为了验证ALE数值模拟方法的可靠性，对文献[18]中的实验进行了分析，面外正六边形蜂窝臂长为3.75 mm，壁厚0.08 mm，高度20 mm，夹芯结构边长为250 mm，两板的厚度均为1 mm，背板的边界条件为四边简支，其他部位不设置边界条件。蜂窝夹芯结构中心外70 mm处将会受到3.1 g三硝基甲苯炸药的水下爆炸冲击。仿真得到的结果如图3和4所示。

图3 水下爆炸数值模拟面板与芯层变形结果对比

图4 水下爆炸模拟面板底部变形曲线对比

数值模拟中芯层的损伤情况与面板底部变形曲线与文献[18]的结果对比表明，ALE方法的数值模拟结果与文献结果的误差较小，面板与芯层的变形特征基本吻合，ALE数值模拟方法是可靠的。

2 数值模拟结果及分析

针对蜂窝的总吸能、各部分吸能占比、面板最大破口尺寸以及背板中心点位移等蜂窝结构关键参数，以无量纲的归一化处理对蜂窝结构进行综合评价，从而探究泊松比对蜂窝夹芯结构抗爆性能的影响。5种蜂窝结构的泊松比及其计算公式为：

双箭头形[17]：

泊松比为-3.375。

星形[9]：

泊松比为-1.74。

内凹六边形[13]：

泊松比为-0.824。

正六边形[13]：

泊松比为1。

四角星形：泊松比为0。

2.1 面板最大破口尺寸

图5给出了蜂窝夹芯结构面板的最大破口尺寸。结合图5可以看到：

图5 蜂窝夹芯结构面板最大破口尺寸

1)泊松比数值最小的为双箭头形蜂窝，其面板不出现破口，当-3.375≤υ<-1.74时，随着泊松比增大，破口尺寸增大，原因是υ数值越大则蜂窝结构的负泊松比特性越弱，压阻效应[17]越难体现，故削减了负泊松比蜂窝结构的抗爆性能；

2)当-1.74≤υ<-0.824时，泊松比增大，压阻效应减弱，但由于内凹六边形蜂窝的t/l相对较小，芯层的变形能力增大，有利于芯材吸收爆炸冲击能量，所以内凹六边形蜂窝面板的破口尺寸减小；

3)当υ=0时，零泊松比四角星形蜂窝不会产生负泊松比压阻效应，但该蜂窝的t/l进一步减小，蜂窝芯层产生更大面积压缩变形来抵抗爆炸荷载，所以蜂窝结构面板破口尺寸没有明显变化。

4)当υ>0时，正六边形蜂窝结构的泊松比为正、而且t/l较大，导致蜂窝结构的变形能力下降，对爆炸冲击能量的吸收也相应减弱，故该结构抵抗爆炸荷载能力较差，破口尺寸增大。

2.2 蜂窝夹芯结构的背板中心点位移

若蜂窝结构背板的变形过大，就会与主体结构发生碰撞，为了避免这种情况，使蜂窝夹芯结构的背板变形更小成为研究的一个目标。

从图6和表3可知，就负泊松比蜂窝结构而言，双箭头形蜂窝结构的背板中心点位移最小，随着泊松比增大，负泊松比的压阻效应变小，削弱了负泊松比蜂窝结构的抗爆性能；当泊松比为0时，背板中心点位移最小，虽然零泊松比蜂窝在变形时不会产生有利于抗冲击的压阻效应，但由于其t/l小，蜂窝夹芯结构的闭合性较好，芯层能够进行更大范围的变形以抵抗爆炸荷载。

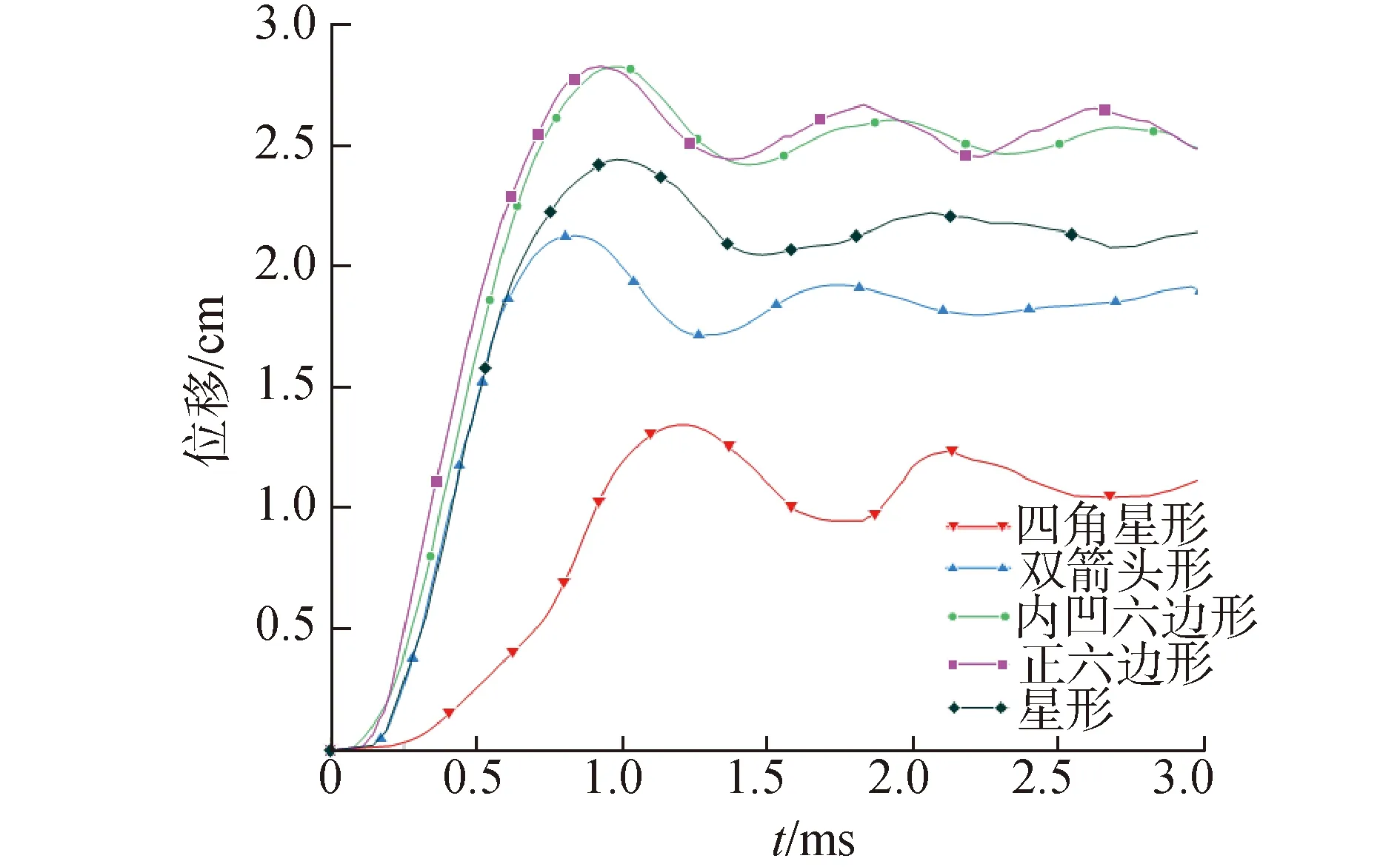
图6 5种蜂窝夹芯结构背板中心点位移时程曲线

表3 背板中心点位移

由图7可见，5种蜂窝结构背板达到最大位移时，零泊松比四角星形蜂窝芯层的压缩变形最大，所以背板中心点位移最小；正六边形蜂窝的泊松比为1，其力学特性不利于承受爆炸荷载，故背板的中心点位移较大。

2.3 蜂窝夹芯结构的能量吸收

通过对双箭头形、星形、内凹六边形、零泊松比四角星形和正六边形蜂窝夹芯结构的数值模拟，可以得到各个结构的总吸能和各部分吸能，如图8、表4所示。

图8给出了蜂窝夹芯结构各部分的吸能占比。就芯层来说，从双箭头形蜂窝开始，随着υ的增大，芯层的吸能占比也减小；当υ=0时，芯层吸能占比稍微有所提高；若泊松比继续增大，芯层的吸能效率却再次降低。

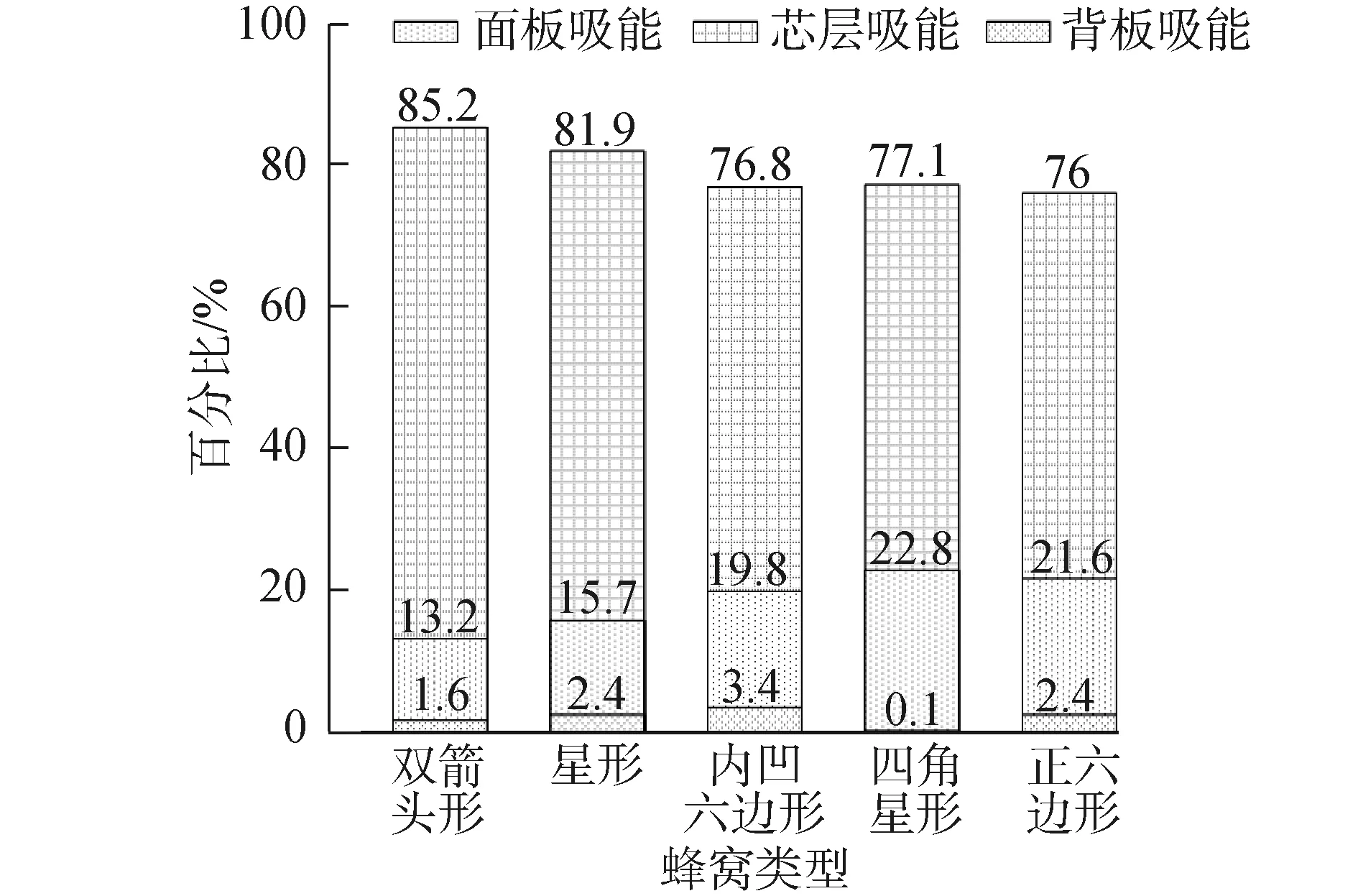
图8 蜂窝夹芯结构各部分吸收能量占比

当υ<0时，如表4所示，随着υ增大，结构的总吸能先增大再下降。由于双箭头形蜂窝的泊松比最小，芯层的压阻效应最明显，由图7可知，蜂窝芯层中心点处的密度大，抵抗变形能力强，所以芯层的吸能占比是蜂窝结构各部分中最高的，但结构整体变形较小，故总吸能不多；星形蜂窝的负泊松比效应小，但整体压缩变形要大于双箭头蜂窝，所以总吸能有所提高；内凹六边形蜂窝结构的负泊松比的压阻效应相对不明显，抵抗爆炸荷载和能量吸收的能力差，因此，内凹六边形蜂窝结构的总吸能较小。

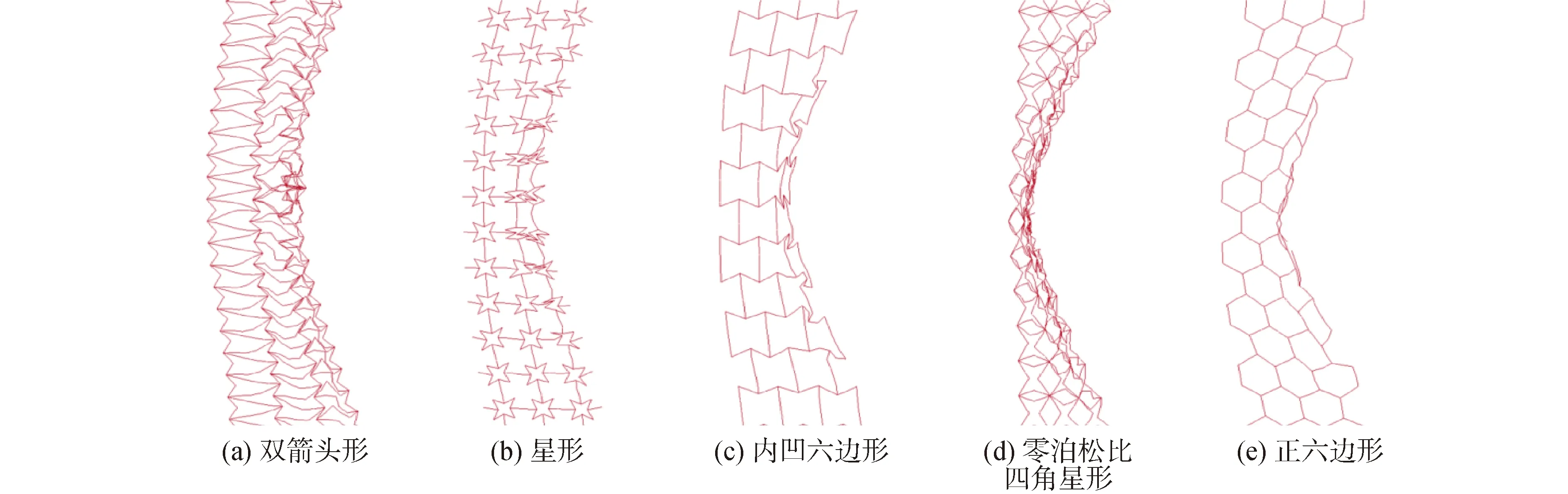
图7 5种蜂窝结构背板位移最大时芯层变形

表4 5种不同蜂窝夹芯结构的总吸能

当υ=0时，零泊松比四角星形蜂窝的t/l只有0.046。由于局部刚度小，芯层会产生更大范围的压缩和变形，这种大面积的压缩变形有利于能量的吸收，所以零泊松比四角星形蜂窝结构的总吸能最多。

当υ>0时，正六边形蜂窝结构相对于其他蜂窝结构来说，变形时不会出现压阻效应，而且t/l也较大，这些特性不利于能量的吸收，使得正六边形蜂窝结构的总吸能最少。

2.4 蜂窝结构综合性能评价

为了综合评价蜂窝夹芯结构的抗爆性能，本文以破口尺寸、背板中心点最大位移和总吸能为基准，将5种蜂窝结构的破口尺寸、背板中心点最大位移和总吸能值进行无量纲的归一化处理[19]并进行三者加权作为评价准则。总吸能的归一化处理公式为：

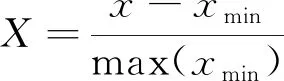
(7)

由于破口尺寸与背板中心点最大位移的评价标准与总吸能相反，所以归一化处理公式为：

(8)

三者的加权评价公式为：

(9)

式中：Y为最终得分；X′1为横向破口尺寸的归一化数值；X′2为纵向破口尺寸的归一化数值，X′3为背板中心点位移的归一化数值；X为蜂窝总吸能的归一化数值，最后得到的蜂窝结构抗爆性能评价如表5所示。

表5 蜂窝夹芯结构抗爆性能评价

在破口尺寸、背板中心点最大位移和总吸能经加权后得到的抗爆性能评价中，评价最高的为零泊松比四角星形蜂窝，最低的是正六边形蜂窝。所以，抗爆性能表现最优的是零泊松比四角星形蜂窝结构。

3 结论

1)四角星形零泊松比蜂窝芯层变形量大，对面板起到了很好的冲击缓冲作用，破口尺寸最小拥有最好的抗爆性能；负泊松比蜂窝芯层负泊松比特性显著，其吸能占比最大且随泊松比的减小而增大，抗爆性能次之；六边形正泊松比蜂窝夹芯结构的破口尺寸最大，芯层吸能占比最低，抗爆性能最差。

2)在高速爆炸荷载作用时，结构会产生很强的惯性效应，负泊松比蜂窝夹芯结构的负泊松比特性会被削弱，使得内凹六边形和正六边形蜂窝的背板中心点位移相差较小。

3)在蜂窝抗爆结构几何参数设计时，应适当减小蜂窝胞元的t/l，以进一步增大芯层的变形，降低夹芯结构面板和背板受到的冲击载荷。