碟簧自复位防屈曲支撑滞回性能试验与模拟

丁玉坤， 刘洋涛

(1.哈尔滨工业大学 结构工程灾变与控制教育部重点实验室，黑龙江 哈尔滨 150090； 2.哈尔滨工业大学 土木工程智能防灾减灾工业和信息化部重点实验室，黑龙江 哈尔滨 150090； 3.哈尔滨工业大学 土木工程学院，黑龙江 哈尔滨 150090)

构造合理的防屈曲支撑具有良好的延性和耗能能力，常用于有抗震要求的中心支撑钢框架结构中[1-2]。研究表明，防屈曲支撑大幅屈服卸载后残余变形较大[3]，不利于震后结构的修复。文献[4]指出，当结构经历大的地震作用后层间残余角超过0.5%时，震后进行修复所需费用将超过重建的费用。文献[2]对墙板内置支撑钢框架试验表明，当加载侧移角为1.0%时，残余侧移角已超过0.5%，当加载侧移角为2.0%时，残余侧移角为1.2%～1.5%，远大于0.5%。因此，有必要探讨合理的支撑构造来减小防屈曲支撑的残余变形。文献[5]采用形状记忆合金棒提供复位力的自复位防屈曲支撑试验研究表明，大幅侧移下，支撑的残余变形约为加载侧移的一半。采用钢绞线提供复位力时，因支撑的变形能力严重受限于钢绞线的弹性变形能力，因此又采用多重套管[6]或采用复合纤维筋[7]来增大支撑的弹性变形能力。上述试验研究中，将复位系统锚固端焊接在防屈曲支撑两端[5-7]，当为复位系统施加预拉力后，防屈曲支撑将有初始预压力，可能对防屈曲支撑的受力不利。实际应用中，当设计一根支撑时，可采用防屈曲支撑或自复位防屈曲支撑。采用自复位防屈曲支撑后，因复位系统常是支撑承载力的主要来源，与采用纯防屈曲支撑相比，设计轴力相同的情况下，自复位支撑中的防屈曲支撑部分的承载力将被大幅削弱。在经历相同的楼层侧移时，当复位系统采用预拉的筋棒等几乎不耗能的材料[6-7]时，与纯防屈曲支撑相比，自复位防屈曲支撑的耗能将被大幅削减，不利于结构的耗能。此外，预压碟簧也可提供复位力，文献[8]采用碟簧组合的自复位支撑研究中指出，为了简化复位系统力学模型和使复位系统更加有效地提供复位能力，建议减小碟簧间的摩擦。然而，若能明确碟簧间的摩擦机制，合理采用碟片叠合后再对合的复合组合碟簧[9]不仅可提供复位力，还有望提供额外的耗能能力。

基于上述考虑，本文采用预压复合组合碟簧构建复位系统，通过灵活调整碟簧组合方式来满足支撑的复位力和变形能力的需求，并通过碟簧叠合面间的摩擦为支撑补充耗能。采用组装构造，当复位系统施加初始预压力后不会对防屈曲支撑产生初应力。同时，组装构造还将便于检修和更换支撑，并可重复利用支撑使用过程中保持完好的部件。

本文通过设置推拉杆以及交错内外螺杆等构建出支撑拉、压作用下复合组合碟簧始终受压的新型复位系统。通过拟静力试验和数值模拟重点考察了组装的碟簧自复位防屈曲支撑构造形式、复位比率等对支撑滞回性能和残余变形的影响。

1 试验概况

1.1 试件的构造

试验包括3个自复位防屈曲支撑(SCB1、SCB2和SCB3)试件(见图1)、一个仅设置复位支撑(self-centering,SC)的试件和一个仅设置防屈曲支撑(buckling restrained brace,BRB)的试件。试件的设计和细部构造详见文献[10]，使塑性变形集中在钢板支撑上，其他部件处于弹性。钢板支撑材性实测值见表1，伸长率为30.34%，实测厚9.68 mm。在SCB1、SCB2、SCB3和BRB中，钢板支撑屈服段实测宽度依次为30.10、40.12、50.14和50.12 mm。此外，碟簧钢材采用60Si2MnA，表1中给出了碟簧厂家提供的碟簧钢材的屈服和极限应力。

表1 钢材的材性

1)复位系统的构造和工作机理。

在钢板支撑两侧配置2个相同的复位系统(图1和图2)。每个复位系统由两端的推拉杆、内、外螺杆和中部的预压碟簧系统连接形成，见图2(a)，内、外螺杆为各4根直径16 mm的两端带螺纹的8.8级高强螺杆。每个预压碟簧系统中，采用2片碟簧叠合为一组，然后48组对合的组合碟簧。根据文献[9]，采用A系列无支撑面碟簧，碟簧尺寸见图1(b)。单片碟簧最大设计轴向压缩变形f为0.75h0=1.65 mm。导杆直径为50 mm，一方面为碟簧组合施加预压力；另一方面充当碟簧组合的导向杆。导杆施加预压力后，导杆、两推拉块和碟簧组合形成一个自平衡的受压碟簧系统，见图2(b)，然后再经交错的内外螺杆与两端的推拉杆连接，见图2(a)。整个支撑受压时，推拉杆直接推动推拉块进一步压缩碟簧组合；受拉时，一端的推拉杆经4根内(或外)螺杆拉动另一端的推拉块，同样可实现进一步压缩碟簧组合(图2(a))。进一步压缩的碟簧组合便可提供复位力。当外力达到预压力后进一步压缩碟簧组合时即为复位系统“启动”。

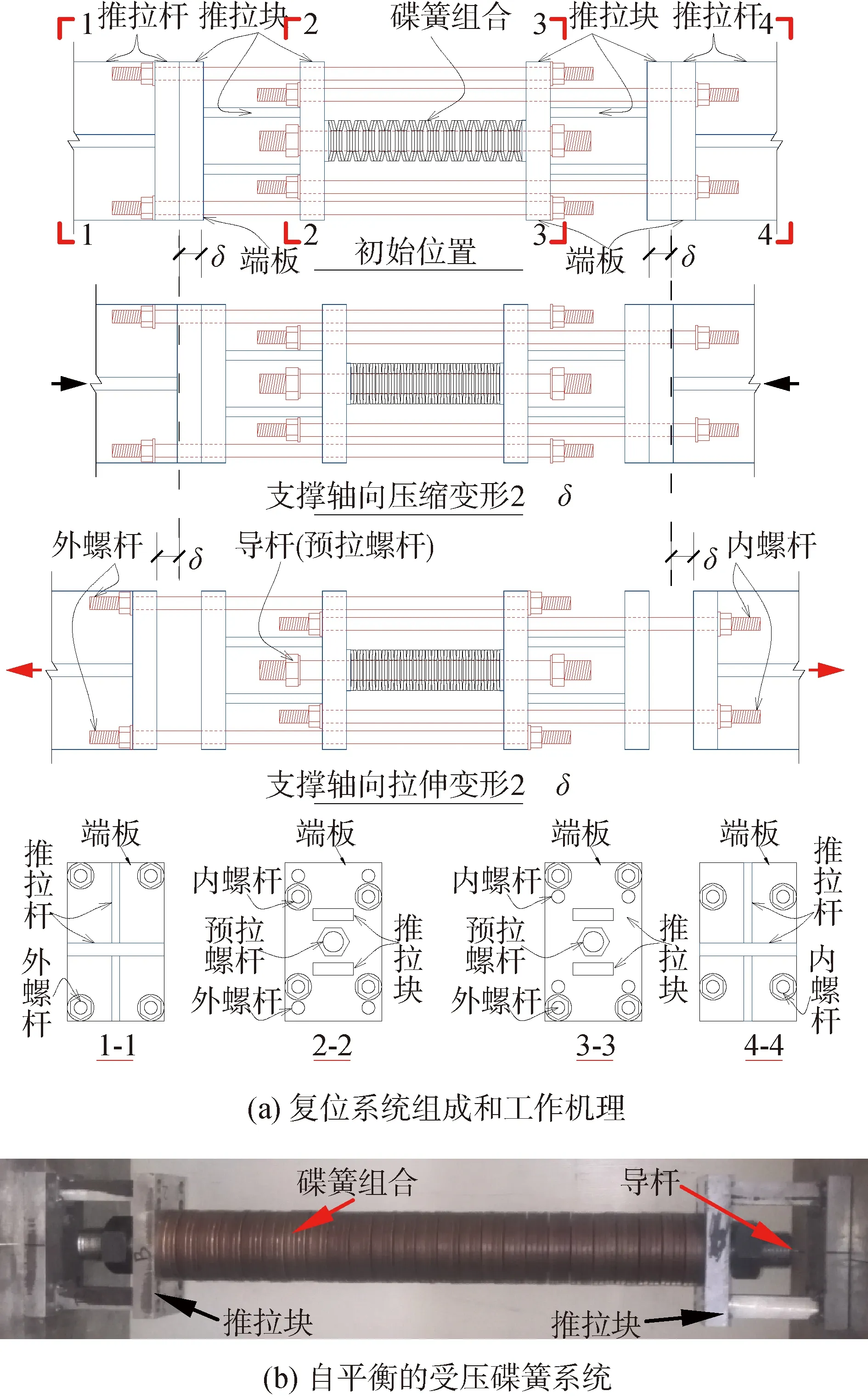
图2 复位系统的工作机理

2)防屈曲支撑的构造。

防屈曲支撑由外部约束构件和内置钢板支撑组成，见图1。约束构件由焊接的开孔帽型钢(由2个不等边角钢和一块钢板焊接成)、开孔约束钢板、开孔填板通过10.9级M12高强螺栓连接组成。每根内置钢板支撑由两端的弹性段、过渡段以及中部的屈服段组成，见图1(a)。

约束构件与钢板支撑间沿钢板支撑厚度和宽度每侧的间隙为0.2 mm和1.5 mm。同时，在钢板支撑屈服段上端留置45 mm的轴向空隙(图1(b))，以避免支撑轴向压缩时钢板支撑直接挤压约束构件内的开孔填板。组装前，在钢板支撑表面涂刷润滑脂来减小钢板支撑与约束构件间的摩擦力。钢板支撑两端通过10.9级M20高强螺栓与整个自复位支撑端部的节点板进行连接(图1)。

图1 自复位防屈曲支撑的构造和组装

3)自复位防屈曲支撑的构造。

自复位防屈曲支撑由两端的端部连接部件将上述防屈曲支撑和复位系统并联在一起，构造和组装过程见图1(图1中组装用高强螺栓未画出)。复位系统两端的推拉杆与端部节点板焊接连接，防屈曲支撑的钢板支撑通过拼接板和高强螺栓与端部节点板连接。为了便于试件安装在加载装置中，在试件两端焊接20 mm厚的上、下部连接端板。组装过程中，钢板支撑和两端连接部件先就位(图1(a))，然后将钢板支撑附近的约束部件和受压碟簧复位系统等进行组装(图1(b))，最后用帽形钢将复位系统和内置钢板支撑封装起来(图1(c))。需注意的是，为避免钢板支撑承受初始装配应力，待复位系统安装后，再将钢板支撑两端的高强螺栓进行终拧连接。在约束构件与复位系统中的推拉杆及推拉块间约留置2 mm的间隙(图1(c))，这样约束构件不但可为钢支撑提供垂直支撑轴向的支承，且可为受压复位系统提供侧向约束，有利于确保整个支撑受压时的稳定性。每根自复位防屈曲支撑SCB是将防屈曲支撑和复位系统同时采用，当将SCB的受压碟簧系统和内、外螺杆去掉后为纯防屈曲支撑试件(BRB)，当将SCB的钢板支撑去掉后为纯自复位支撑试件(SC)。

自复位支撑的复位比率αsc定义为整个自复位系统预压力与钢板支撑屈服后某侧移角下防屈曲支撑的受压承载力Ncmax=βωNy的比值。ω和β为钢板支撑的承载力调整系数[1-2]，屈服轴力Ny=Acfy。

1.2 试验方案

试验加载方案见图3。加载通过控制试件上端水平位移Δ来往复施加水平力P，约定使试件受压的位移为负向；使试件受拉的位移为正向。各试件加载位移历程见文献[10]。为了考察多次试验中SC性能是否变化，试验的先后次序为SC-1、SCB-1、SCB-2、SCB-3、SC-2和BRB。

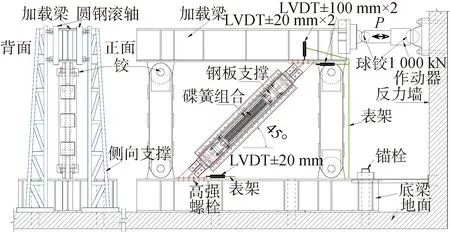
图3 装有支撑的加载装置

1.3 试件的破坏现象

虽然碟簧组合经历了3个自复位防屈曲支撑和2个纯自复位支撑试验，碟簧组合处于弹性和保持完好。试件最终均发生钢板支撑屈服段低周疲劳受拉断裂[10]。除了钢板支撑受拉断裂，其他部件均保持完好并在多次试验中重复利用。

在水平位移幅值±46.67 mm(对应侧移角为3%)内，试件SCB-1、SCB-2、SCB-3和BRB的钢板支撑分别在经历受拉最大水平位移幅值38.2 mm、31.0、35.4和30.2 mm后断裂。因钢板支撑屈服段长度为886 mm，可得屈服段断裂前经历的最大轴向受拉应变约为2.41%～3.05%。可见，采用拼接板和螺栓连接内置钢板支撑的构造，如图1所示，减小了支撑屈服段长度，可进一步改进端部连接来增长屈服段，进而降低屈服段的受拉应变值和改善疲劳性能。

1.4 试件的荷载-位移曲线

试验中量测了支撑上下端的相对水平位移Δ和水平力P。试验给出的轴向荷载-位移曲线见图4。根据支撑倾角，支撑水平位移Δ约为轴向位移δ的1.414倍，支撑轴力F约为水平力P的1.414倍。可见，直至钢板支撑断裂破坏前，试件SCB-1、SCB-2、SCB-3和 BRB的滞回曲线稳定，BRB的曲线呈饱满的纺锤形。SCB-1、SCB-2、SCB-3以及SC-1和SC-2的曲线呈旗帜形。SC-1和SC-2滞回曲线几乎重合，表明复位系统受力性能稳定。

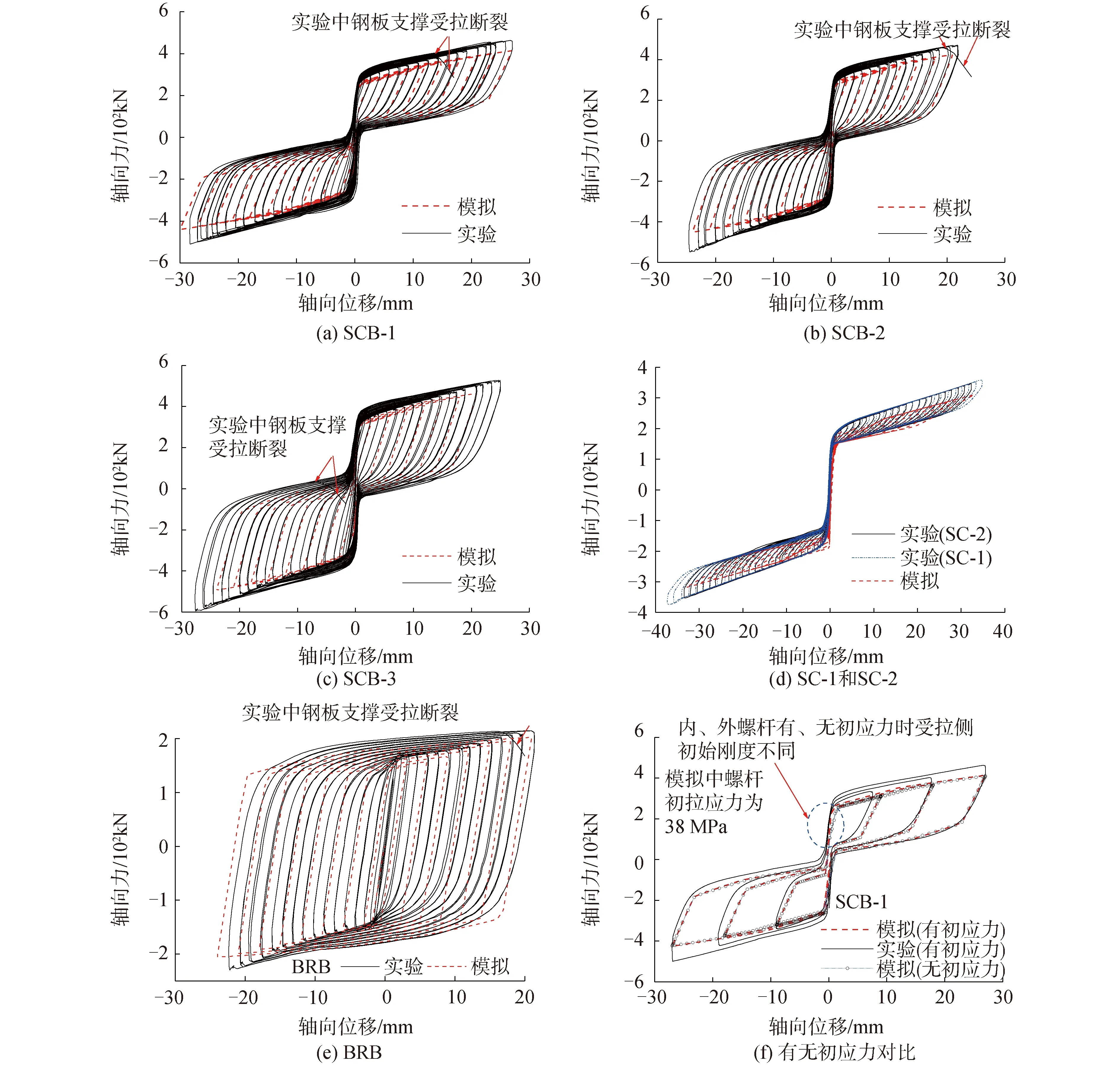
图4 滞回曲线

1.5 复位比率及对残余变形的影响

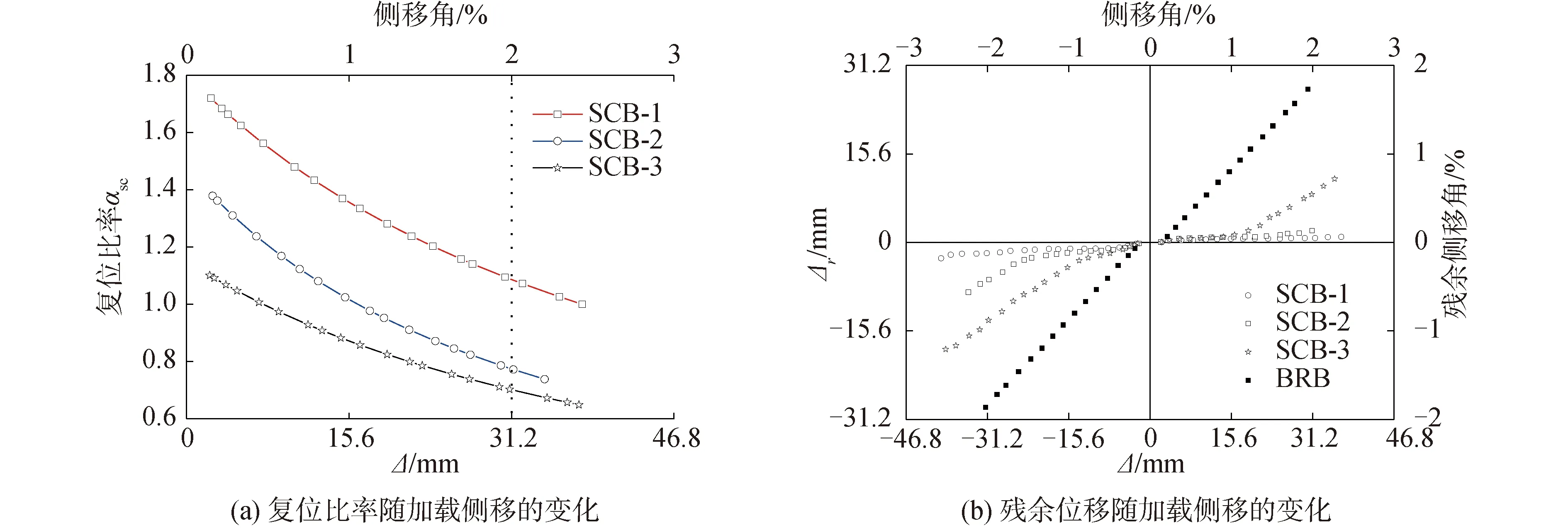
图5 复位比率和残余位移随加载侧移的变化

2 数值模型的建立

采用ABAQUS建模，试件建模见文献[10]。依据试验位移加载幅值[10]，模拟中考虑计算耗时和改善收敛性，采用轴向加载，每级循环一圈。

2.1 自复位系统的建模

碟簧采用壳元模拟，2片叠合碟簧间建立面-面接触。经大量试算且与试验碟簧组合的压缩试验比较，取叠合面间摩擦系数为0.4[10]。由图6可见，受压碟簧系统的试验和模拟曲线较一致。推拉杆、推拉块采用壳单元S4R模拟。内、外螺杆以及导杆采用桁架单元T3D2模拟，因试验中只承担拉力，故模拟中使其具有只受拉不受压的力学特性。内、外螺杆的两端分别与推拉块端板和推拉杆端板建立耦合(图7(a))。推拉块端板与推拉杆端板之间分别建立面-面接触(图7(b))。

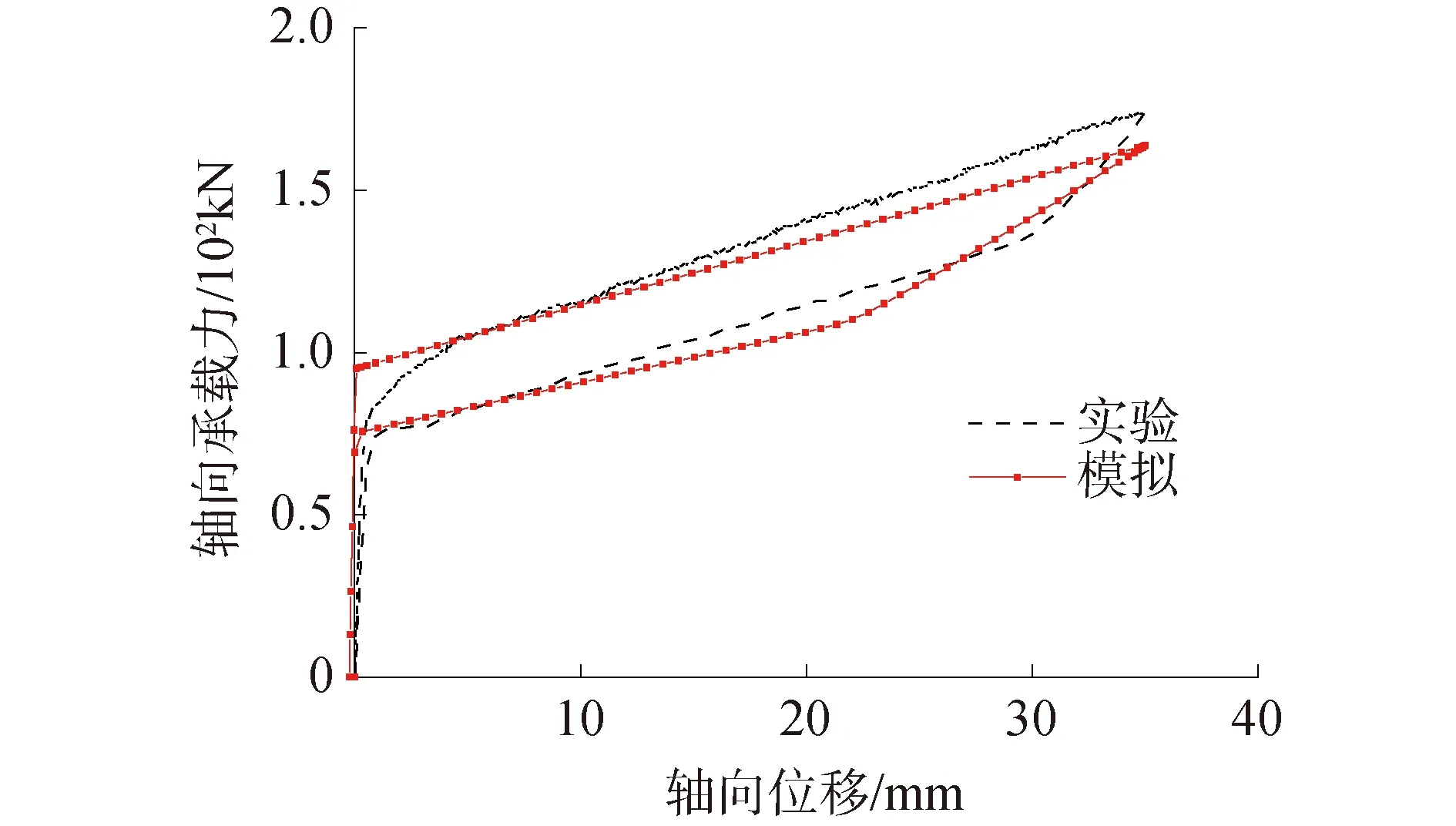
图6 受压碟簧系统轴向受压

因试验中约束构件和端部连接系统无塑性发展和破坏，为简化建模，建立两端采用带有节点板的推拉杆(图7)，不再额外建立端部连接系统。约束复位系统横向运动，允许轴向运动，这样，略去外围约束构件。此外，上述建模过程中，依据试验实测的内、外螺杆初始装配应力，对内外螺杆施加了初始应力，待受压碟簧系统自平衡体系建立完成后，内、外螺杆的初始拉应力大小为38 MPa[10]。

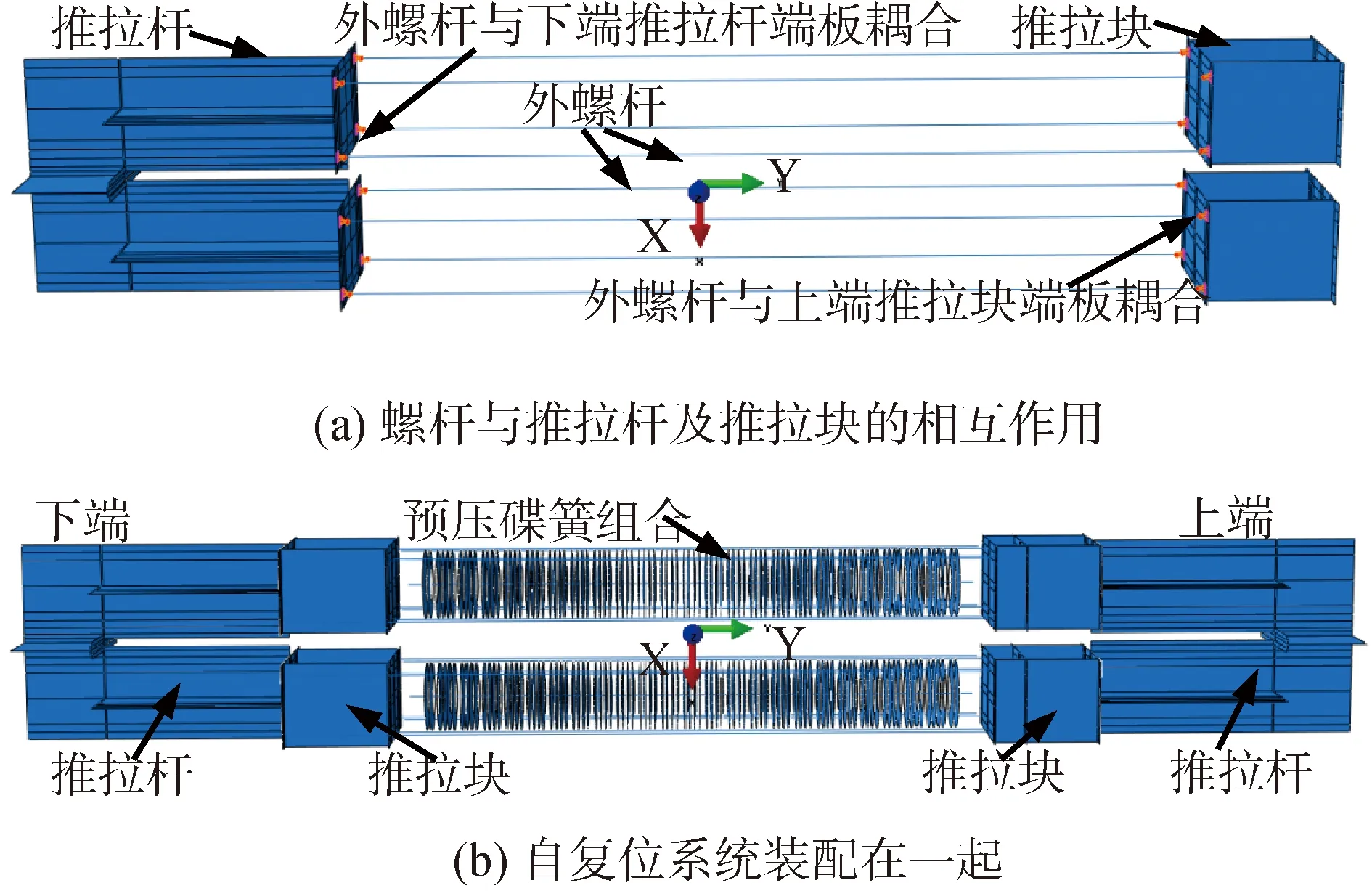
图7 纯自复位支撑的模型

纯自复位支撑的模拟和试验的轴向滞回曲线见图4。可见，相同位移下模拟的承载力和耗能小于试验的，这主要是由模拟中摩擦力小于试验引起的。一方面，模拟中没有计入复位系统内部件间可能的摩擦作用；另一方面，与试验相比，模拟中只考虑了碟簧叠合组合时的摩擦作用，忽略了其他部件间可能的摩擦作用。总体上，模拟给出的荷载-位移曲线与试验较一致，表明该模型可行。

2.2 防屈曲支撑的建模

钢板支撑采用壳元S4R模拟，材性实测值见表1。因试验中钢板支撑未失稳破坏，约束构件保持完好，为简化建模，忽略了外围约束构件，仅建立钢板支撑，并约束其横向位移，使其不发生失稳。

钢板支撑采用混合强化模型来模拟，其强化参数取值为C=4 000 MPa、γ=37、Q∞=60 MPa、b=5，模拟中，钢板支撑弹性段与两端节点板采用Tie约束模拟试验中没有出现滑移的高强度螺栓连接，下端固定，通过上端进行轴向往复加载。模拟和试验的轴向荷载-位移曲线见图4。可见，与受拉时相比，因模拟中未能体现试验中钢板支撑发生多波失稳后与约束构件间的摩擦作用[10]，导致模拟得出的BRB的受压承载力低于试验值较多。但总体上，模拟与试验曲线较一致，表明上述模拟是合理的。

2.3 自复位防屈曲支撑SCB的建模

在上述自复位系统建模后，再将钢板支撑两端与节点板连接，从而实现复位系统与钢板支撑并联受力(图8)，并避免钢板支撑承受初始应力。

图8 SCB模型

图4为3个SCB的模拟与试验滞回曲线，可见模拟曲线也呈明显的旗帜形。SCB支撑模拟所得拉压两侧的承载力小于试验值，这是由前述纯自复位支撑和防屈曲支撑的原因综合影响的。模拟也表明，其他构造不变时，支撑承载力和残余变形均随钢板支撑横截面的增大而增大。SCB-1复位效果最好，SCB-3的最差。3个SCB试件的模拟与试验结果较为一致，表明模型建立是合理的。此外，以SCB-1为例(SCB-2和SCB-3也类似)，由图4还可见，内、外螺杆均无初应力导致受拉侧初始刚度降低。这表明，还可适当控制内、外螺杆的初拉应力来调节自复位支撑受拉侧的初始刚度。

3 构造影响分析

3.1 构造参数

考察了碟簧组合初始预压量(预压力)和叠合面间的摩擦、钢板支撑屈服段截面和长度、内外螺杆截面和初拉力的变化对支撑滞回性能的影响。

选取A系列3种碟簧(等效为无支撑面碟簧建模)：D=100、d=51、t=7；D=160、d=82、t=10；D=250、d=127、t=14(D、d、t分别为碟簧外径、内径和厚度，mm)[9]。采用复合组合的碟簧组合方式，对合组数分别为24、30、48，每个对合组合中采用2片叠合。碟簧间摩擦系数μ取0.4。依据试验支撑构造(见图1)，模拟中自复位支撑总长取支撑轴线与上下端连接端板内部表面交点间的距离，即总长2 206.2 mm(对应支撑的垂直高度为1 560 mm)。为简化分析，略去了推拉杆端部以外弹性段的长度，取支撑总长1 945.4 mm。钢板支撑屈服应力为298.29 MPa，厚度为10 mm，屈服段截面Ac相应变化，钢板支撑屈服段长度l=886 mm(总长度L=1 706 mm)。对应D=100、D=160和D=250的碟簧采用的内外螺杆规格依次为M20、M24和M30；对应导杆直径依次为50、81和126 mm。在上述构造的基础上，改变所考察的构造参数形成一系列分析模型[10]。

3.2 构造影响分析结果

1)碟簧预压量的影响。

保持其他参数不变，经改变碟簧组合初始压缩量来调节初始预压力。由图9(a)可见，相同加载位移幅值下SCB承载能力随预压量的增加而提高，残余变形减小。其他碟簧规格下规律与此类似。

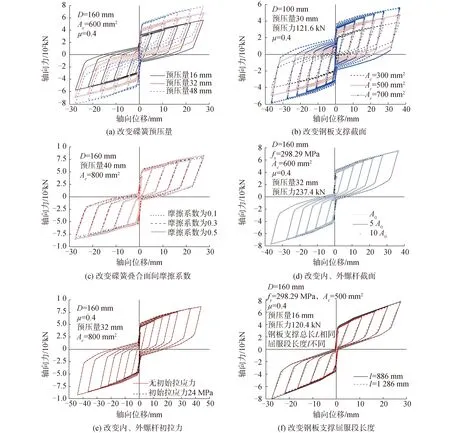
图9 不同构造对SCB支撑轴力-轴向位移曲线的影响

2)钢板支撑屈服段截面的影响。

其他参数不变时，钢板支撑屈服段截面Ac增大后，相同加载位移下复位比率减小，SCB的残余变形增加(图9(b))。这与试验试件受力性能一致。特别是，当自复位系统的初始预压力被钢板支撑屈服后的承载力超过后，支撑的残余变形增幅明显。

3)碟簧叠合面间摩擦系数的影响。

其他参数不变时，对摩擦系数μ在0.1～0.6的算例分析表明，相同预压量下，自复位系统的预压力以及自复位系统启动后加载阶段刚度均随摩擦系数增大而增大(图10)。随摩擦系数增大，自复位系统启动后，相同位移下加载与卸载阶段的承载力差值越大，力-位移曲线所围面积越大(图10)，SCB滞回曲线所围面积增大，耗能能力增强(图9(c))。但系数μ越大，支撑卸载后，SC系统的承载力高于BRB的承载力的幅度减小，SCB支撑的残余变形增大(图9(c))。总体上，因防屈曲支撑是SCB的主要耗能部件，上述范围内仅叠合面间摩擦系数的变化对SCB支撑的复位效果和耗能能力的影响不大。系数μ在0.35～0.45时，SCB有较好耗能能力的同时不会过多劣化复位效果。因往复作用下部件间实际存在的摩擦区域较多，自复位支撑中摩擦区域不仅局限于碟簧组合间，应进一步探讨摩擦系数合理的取值范围。

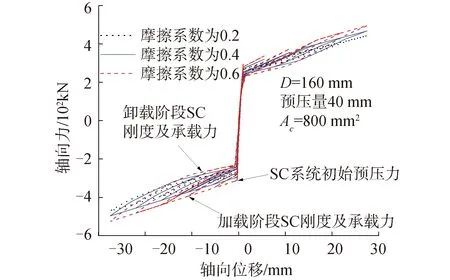
图10 摩擦对复位系统的影响

4)螺杆截面的影响。

内、外螺杆的截面面积大小会影响螺杆刚度，进而影响支撑受拉刚度。取基准螺杆截面A0=452.4 mm2，对应M24。分析表明，当螺杆截面大于基准螺杆截面后，增大螺杆截面对SCB受力性能的影响很小，特别是増至5A0后，不能进一步改善支撑滞回性能，也不经济。因此，螺杆截面不宜过大。同时，螺杆的轴向拉应力随螺杆截面增大而降低。为了实现支撑拉、压两侧受力更加均衡，避免螺杆截面和受拉刚度的降低导致自复位系统的受拉时启动位移增大，螺杆截面不宜过小。设计中，在支撑最大受拉承载力的范围内，应确保螺杆处于弹性(应力小于其屈服应力)。本文试验中，采用D=100的碟簧时，螺杆最大拉应力为247 MPa。模拟中，采用D=250、D=160和D=100时，对应的螺杆最大拉应力分别为160、150和170 MPa。综上，建议控制螺杆最大拉应力与其屈服应力之比为0.2～0.5，且采用8.8级的高强螺杆。

5)螺杆初始拉力的影响。

为深入分析初始拉力的影响，取M24螺杆，螺杆初始预拉应力分别为14、24和32 MPa。与试验(图4)一致，模拟表明，与螺杆无初拉力相比，SCB受拉侧的启动前刚度随初始拉力的增大而逐渐增大，拉压两侧初始刚度更一致(图9(e))。拉应力为32、24、14 MPa时，对应的内(或外)螺杆总初始拉力与碟簧组合预压力的比值分别为49%、36%和21%，且初始拉应力从24 MPa増至32 MPa时，SCB滞回性能和初始受拉刚度提升不大。此外，试验中整个自复位系统的预压力约170 kN，外、内螺杆总预拉力分别约75 kN 和48 kN，则外、内螺杆总预拉力与整个复位系统预压力之比约分别为44%和28%，均值约36%。试验表明，螺杆预拉力的施加使支撑拉压作用下的初始刚度和受力性能更一致(图4)。因此，为使SCB初始拉压刚度较一致，建议取外(或内)螺杆的总预拉力为整个自复位系统预压力的30%～40%。

6)屈服段长度的影响。

保持自复位系统和钢板支撑总长不变时，随屈服段增长，相同加载位移下屈服段应变减小，BRB部分以及整个SCB的承载力降低(图9(f))，相同加载幅值下复位比率增大。卸载后，SC部分的承载力高出BRB部分的承载力较多，残余变形减小。结合试验和模拟结果，为改善支撑低周疲劳和复位效果，应改进构造来尽可能增大屈服段长度。

3.3 复位比率对残余变形影响分析

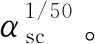
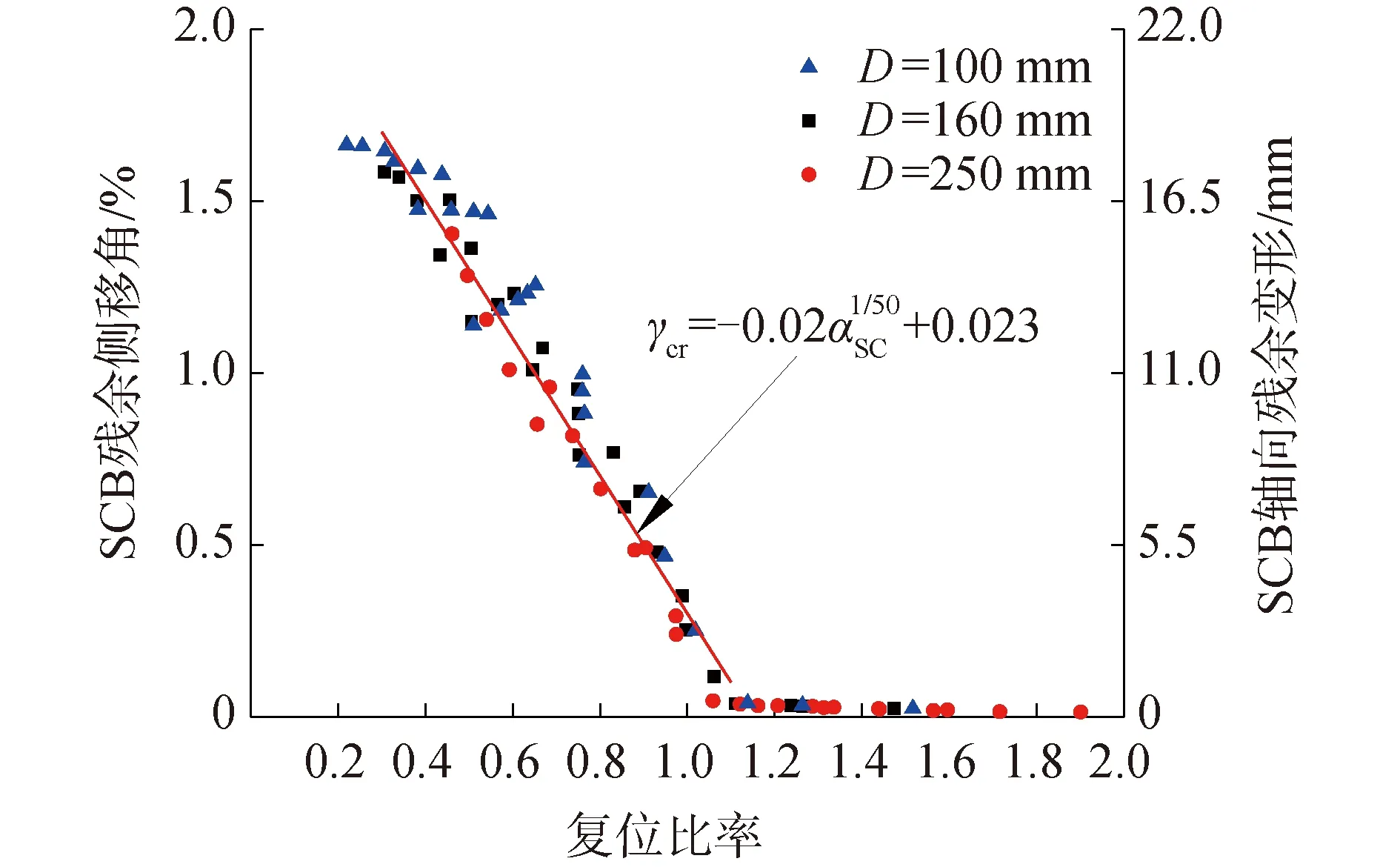
图11 复位比率对残余变形的影响

4 结论

1) 试验和模拟表明，可进一步改进构造来增大钢板支撑屈服段长度，从而减小残余变形和最大受拉应变，并改善低周疲劳性能。建议内、外螺杆采用8.8级高强螺杆时，螺杆最大工作应力与屈服应力之比宜控制在0.2～0.5。为使SCB初始拉、压刚度较一致，建议全部外(或内)螺杆的总预拉力取整个自复位系统预压力的30%～40%。

3)采用复合组合碟簧的复位系统，在满足复位功能的前提下，碟簧叠合面间的摩擦还可提供额外的耗能，有益于支撑的抗震性能。自复位防屈曲支撑的塑性变形集中在内置钢板支撑上，其余部件保持完好，便于支撑检修和重复利用组成部件。