碟形弹簧弹塑性有限元分析研究

王朝晖 王晓丽



碟形弹簧弹塑性有限元分析研究

王朝晖 王晓丽

（北京航天动力研究所，北京 100076）

为了分析不同计算手段得到的碟形弹簧载荷特性之间的差异以及摩擦系数等因素对载荷特性的影响，本文借助有限元手段对某发动机用碟形弹簧进行了弹性和弹塑性仿真计算，并与GB/T1972推荐公式解进行了对比，通过对不同摩擦系数下的碟簧组合的仿真分析，研究了摩擦系数对碟簧组合特性的影响，得出结论，为发动机的设计提供了重要的参考依据。

碟形弹簧；弹塑性；有限元

1 引言

航天型号结构承载部件广泛采用螺栓联接方式[1]。通常合适的拧紧力矩能够有效地保证导弹各组件之间连接的可靠性，但是螺栓通常还要承受外界交变振动、冲击载荷、温度变化等较为复杂的环境[2]，使用诸如碟形弹簧等防松手段保证螺栓连接零件之间的可靠连接或密封是保证产品质量的关键。

2 研究背景

碟形弹簧（简称碟簧）是一种锥形截面垫圈式弹簧，主要特点是负荷大、行程短、所需安装空间小、组合使用方便，非常适合用在高温工作环境、材料线膨胀系数不匹配或者有冲击振动的连接场合。在螺栓与法兰之间加上若干预紧碟簧，高温下，如果法兰、螺栓等材料线膨胀系数不匹配导致了螺栓预紧力下降，可利用预紧碟簧优异的回弹性能补偿螺栓的热膨胀变形量，以预紧碟簧的小变形量提供足够的预紧力负荷，解决螺栓预紧力下降导致的介质泄漏问题[3]。另一方面，随着可拆卸、可更换、模块化的设计思路在液体火箭发动机研制过程中的延展，许多液体火箭发动机组部件之间的连接由原来的不可拆连接改为了可拆法兰连接，其中便面临着如何在高温、高压以及振动环境中保证可靠的连接和密封问题，使用碟簧便是最佳备选方案之一。碟簧使用特性受诸多因素影响，如碟簧材料特性、表面处理工艺、安装方式、表面摩擦系数等，针对在某发动机推力室身部与喷管延伸段法兰连接位置的某碟簧进行了有限元仿真计算，着重分析了材料弹塑性及碟簧表面摩擦系数等对碟簧特性的影响。

目前大多碟簧计算公式[4，5]都源自于1936年美国学者提出的近似解法[6]，但均存在忽略径向应力等各种各样不同程度的前提假设条件，与碟簧实际工作情形存在一定的差异。有限元技术和计算机技术的快速发展为数值求解各类碟簧问题提供了强有力的手段。借助有限元手段分析了某液体火箭发动机用单片碟簧弹塑性，并比较弹性有限元及近似公式解；然后在不同摩擦系数下有限元计算两片叠合碟簧的弹性及弹塑性，分析摩擦系数对碟簧特性的影响并得到了相关结论，对液体火箭发动机中的碟簧设计和使用提供了重要的指导和参考依据。

3 碟簧几何尺寸

某碟簧结构如图1所示，外径=16mm，内径=8.2mm，碟簧厚度=0.6mm，单片碟簧自由高度0=1.05mm，碟簧压平时变形量的计算值0=0.45mm。

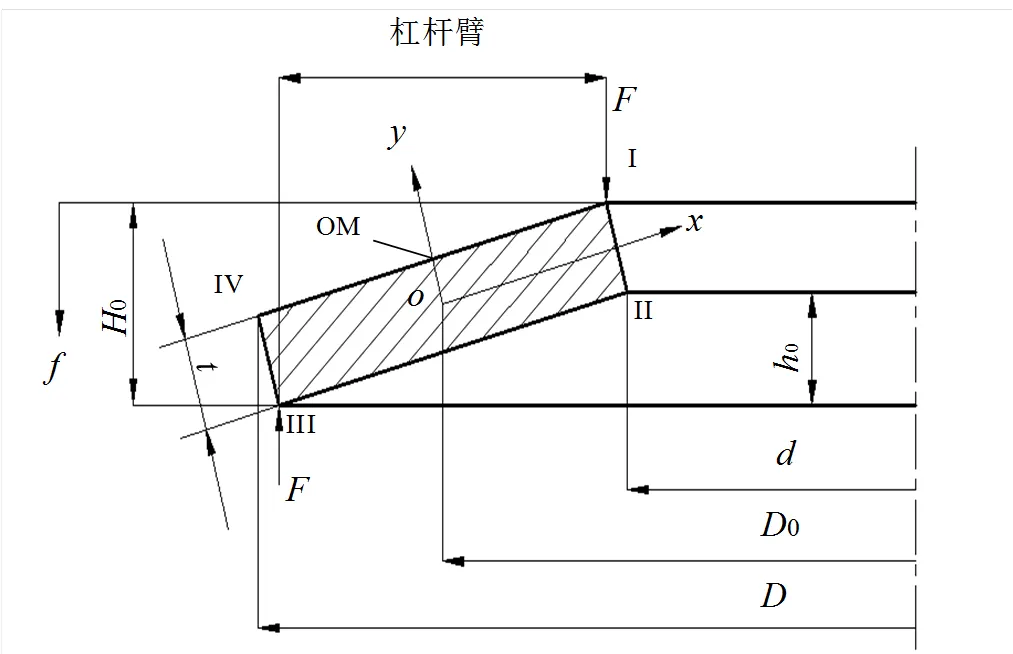
图1 碟簧结构尺寸图

4 有限元模型及计算分析

建立了两种碟簧计算模型：第一种是不包含上下压板，第二种包含上下压板，分别进行了弹性和弹塑性分析。

4.1 不包含上下压板情形

计算采用轴对称有限元模型进行，选择plane182轴对称单元，弹性模量206GPa，泊松比0.3，塑性模型主要考虑屈服准则、硬化准则和流动法则。碟簧材料韧性较好，采用Von Mises屈服准则，硬化准则描述了屈服条件随塑性应变增加的变化情况，采用多线性等向强化模型，流动法则则采用默认的正交流动准则，即塑性流动方向垂直于屈服面[7]。采用大变形几何方程，固定碟簧大端支撑面上圆周所有节点的轴向位移，对碟簧小端支撑面圆周上的节点施加轴向位移载荷[8]，计算网格单元总数1600个，见图2。

图2 计算网格图

对弹性有限元解、弹塑性有限元解与GB/T1972公式近似解进行了比较，见图3。其中GB/T1972近似计算公式描述如下[4]：

——碟簧负荷，——碟簧外径，——碟簧内径，/，——碟簧厚度，0——碟簧最大压缩行程，——碟簧压缩位移量，——碟簧材料弹性模量，——碟簧材料泊松比。

从图3对比情况来看，当碟簧压缩量≤0.750（即≤0.34mm）时，弹性有限元解、弹塑性有限元解和GB/T1972公式近似解三者结果差别很小，当碟簧压缩量＞0.750时，三者之间的差别开始逐渐变大。从碟簧负荷计算结果大小来看，GB/T1972得到的碟簧负荷最大，弹性有限元解次之，弹塑性有限元解最小。表1为碟簧在75%压缩量和完全压平时碟簧计算负荷结果，括号内为相对弹塑性有限元解的误差。当碟簧压缩量在0.750时，三者相对误差9.7%，完全压平时三者结果相对误差16.1%。

从弹塑性结果来看，碟簧在被压平过程中发生了一定的塑性变形，所以卸载载荷曲线低于加载载荷曲线，碟簧自由高度降低了0.04mm，此部分为永久塑性变形，当再次加载—卸载时，碟簧即沿着卸载曲线进行，塑性变形不会增加。

表1 碟簧负荷计算结果 N

4.2 包含上下压板情形

考虑到碟簧实际工作是在螺母与工件之间，增加上下两块压板模拟碟簧实际工作状态。分别进行了弹性和弹塑性分析，上下压板设置为弹性材料，弹性模量设置为碟簧的50倍，即忽略压板的弹性变形量。单元类型选择plane182轴对称单元。计算网格模型见图4，单元总数5834，碟簧单元数量1600。碟簧与上下板之间设置光滑无摩擦接触，下板底面轴向固定，上板顶面设置位移边界。

图4 计算网格（包含上下压板）

不同计算结果下的碟簧负荷曲线见图5。从中可以明显看到，当碟簧压缩量小于0.4mm时，有限元计算碟簧刚度基本保持不变，碟簧负荷呈现线性特性，但是当碟簧压缩量超过0.4mm时，碟簧刚度急剧增加，这与GB/T1972公式以及不包含上下压板有限元方法计算得到的结果有着明显差异，这是因为当碟簧变形超过一定量后，碟簧与上下板之间发生部分接触导致其实际杠杆臂缩短，所以碟簧负荷显著增加。从弹塑性结果曲线来看，碟簧在压平过程中发生了塑性变形，塑性变形量为0.04mm，从三种方法得到的结果大小看，GB/T1972计算得到的值最大，弹性有限元解次之，弹塑性有限元解最小，这与不含上下压板情形得到的结论一致。

将不包含上下压板和包含上下压板两种情况计算得到弹性有限元解及弹塑性有限元解列于图6和图7，也可以明显看到，在碟簧压缩量≤0.4mm时，不包含上下压板和包含上下压板得到的曲线一致，但是当压缩量＞0.4mm时，杠杆臂缩短效应开始出现，碟簧负荷迅速增加。

图6 碟簧负荷曲线对比3

5 摩擦系数对碟簧特性曲线的影响

一般情况下，碟簧以对合、叠合或复合组合的形式存在。由于碟簧之间实际存在一定的摩擦，因此碟簧实际特性曲线与光滑无摩擦情形存在一定的差别。建立了两片碟簧叠合的模型，分别在弹性和弹塑性情况下计算了不同摩擦系数下的碟簧特性曲线。

碟簧与碟簧、碟簧与上下压板之间设置摩擦接触，摩擦模型选择库伦模型，摩擦系数分别设置为0.05、0.14和0.25。计算网格模型见图8。

图8 计算网格

计算结果对比曲线见图9和图10。从图9可以看出，随着摩擦系数的增加，碟簧加载曲线与卸载曲线之间的差值变大，加载与卸载曲线之间围成的面积就是在一个碟簧变形周期内摩擦所消耗掉的能量。摩擦系数增加，所能够消耗的能量也相应增加，因此碟簧组合可以在特定场合用来作为减振隔振元件。

从图9和图10曲线数值大小可以看出，随着摩擦系数增加，碟簧加载负荷增加，卸载负荷减小，这同样说明了在碟簧加载-卸载过程中，摩擦始终起阻碍作用。只有当摩擦系数达到一定程度时，其影响才明显，当摩擦系数不超过0.05时，可以忽略不计，计算误差不超过5%。

图9 不同摩擦系数下弹性有限元结果对比

6 结束语

通过对不包含上下压板及包含上下压板两种情形下碟簧的弹性和弹塑性有限元仿真计算，分析对比了不同计算方法结果的差异，此外还对不同摩擦系数下的碟簧特性进行了仿真计算与分析，得到下述结论：

a. 相同压缩量下，使用GB/T 1972计算方法得到的碟簧负荷最大，弹性有限元结果次之，弹塑性解结果最小；在75%压缩量以内，三者之间的误差相对较小，超过75%压缩量后计算结果差距逐渐变大；

b. 碟簧压缩初始阶段，碟簧负荷与压缩量之间基本呈线性关系，但当碟簧压缩量超过0.4mm后，由于碟簧与上下压板开始接触，杠杆臂变短，碟簧刚度开始急剧增加，负荷显著增大；

c. 碟簧首次加载—压平—卸载后，碟簧发生塑性变形，碟簧自由高度降低0.04mm，再次加载—卸载，碟簧塑性变形不再增加；

d. 对于叠合碟簧，随着摩擦系数增加，碟簧加载负荷变大，卸载负荷变小，特性曲线所围成面积增加，摩擦消耗的功增加；当摩擦系数不大于0.05时，摩擦对碟簧特性负荷计算结果的影响可以忽略不计。

1 郇光周，陈亚玲，杨琪，等. 导弹关键舱段螺栓联接的随机振动响应分析[J]. 航天制造技术，2017(6)：12～16

2 曹鲁光，朱江峰，陈风，等. 基于ANSYS的导弹舱段连接螺栓预紧力仿真分析[J]. 航天制造技术，2014(6)：40～44

3 郑新，陆晓峰. 加氢高压换热器用法兰预紧碟簧有限元分析[J]. 化肥设计，2015，53(5)：10～13

4 GB/T1972—2005碟形弹簧

5 汪曾祥，魏先英，刘祥至. 弹簧设计手册[M]. 上海：上海科学技术文献出版社，1986

6 Almen J O, Laszl O A. The uniform-section disc spring[J]. Trans ASME, 1936, 58：305～314

7 王仁. 塑性力学引论[M]. 北京：北京大学出版社，1992

8 蒲广益. ANSYS Workbench12基础教程与实例详解[M]. 北京：中国水利水电出版社，2010

Elastoplastic Finite Element Analysis of Disc Spring

Wang Zhaohui Wang Xiaoli

(Beijing Aerospace Propulsion Institute, Beijing 100076)

In order to analyze the difference between the characteristics of the disc spring obtained by different calculation methods, and analyze the influence of the friction coefficient on the characteristics,the elastic and elastoplastic finite element simulation of the disc spring was carried out, and the finite element results were compared with the GB/T1972 recommended formula solution. Through the simulation of the disc spring with different friction coefficients, the influence of the friction coefficient on the disc spring characteristics was studied, and some useful conclusions are summarized, which provide an important reference for the design of the liquid rocket engine.

disc spring；elastoplastic；finite element

王朝晖（1989），硕士，航空宇航推进理论与工程专业；研究方向：液体火箭发动机设计。

2018-03-15