用于随动补偿磨损误差机构的开槽碟簧设计*

熊奉奎,张 明*,尹益辉,刘 康,刘 军,刘清兵

(1.绵阳职业技术学院 机电工程系,四川 绵阳 621000;2.中国工程物理研究院 总体工程研究所, 四川 绵阳 621900;3.四川轻化工大学 机械工程学院,四川 自贡 643000)

0 引 言

航空发动机叶片[1],其质量由其材料性能和加工质量共同决定。由于其在高温、高压、大冲击等恶劣环境下工作,且必须兼具形状结构准确、精度稳定性优异、极高的表面质量、轻量化四大工作特性,所以航发叶片一般由极难加工的高温合金或钛合金,经高精度加工而成。因此,这对加工的高端五轴叶片加工机床[2]提出了极高的精度及稳定性要求,也对作为高端机床核心部件的转台提出了极高要求,即必须同时兼具高速、高精度、高精度稳定性和大扭矩的特点[3]26。

针对传统转台磨损后传动间隙增大,导致转台精度稳定性及使用寿命下降的问题,中国地质大学的雷亮和吴涛提出了一种变导程涡轮蜗杆副传动转台;该结构利用蜗杆的轴向齿厚沿其轴线从一端到另一端按比例地增大或减小,而与它啮合的蜗轮的所有齿的齿厚均相等。因此,当蜗杆沿轴线移动时,理论上蜗杆在某一位置上一定会消除蜗杆蜗轮之间的侧隙[4]。但这种结构某些位置侧隙较大,会导致传动精度不稳定。张正刚等[5]提出了一种斜齿轮垫片调整结构转台,其由一个宽斜齿轮与两个同轴且螺旋线错位的窄斜齿啮合的齿轮副组成,通过改变两个窄斜齿轮之间的垫片厚度,达到消除磨损间隙的目的;但其属于刚性调节,不能实现自动补偿。

目前,很多针对转台的研究都转向了力矩电机直驱式转台,因为无中间传动机构,传动精度和效率极高;但力矩电机直驱式转台存在的传动扭矩小、散热差的缺点,仍未得到较好的解决。

鉴于此,本文提出一种非标开槽碟簧随动补偿磨损误差机构,利用非标开槽碟簧优异的变刚度及渐减性位移-载荷特性曲线两大特性,实现对磨损误差的实时随动补偿,达到提高转台精度稳定性和寿命,最终满足航发叶片加工要求的目的,为开槽碟簧的设计与应用提供参考。

1 工作原理

碟簧自动补偿机构结构如图1所示。

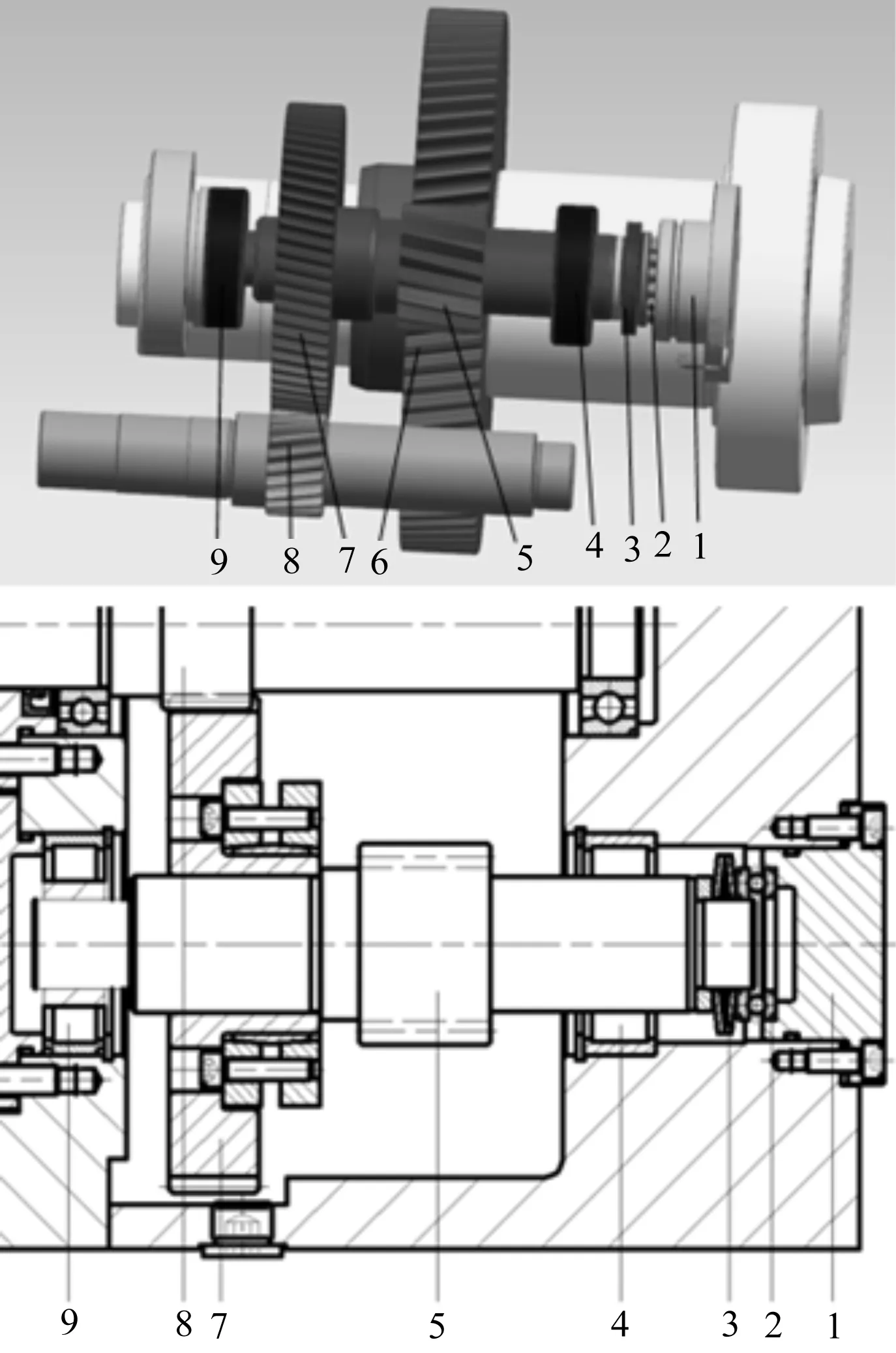
图1 碟簧自动补偿机构结构图1—端盖;2—推力球轴承;3—碟簧;4,9—圆柱滚子轴承;5,8—斜齿轮轴;6,7—斜齿轮

图1中,碟簧3一端与由端盖1定位的推力球轴承2接触,另一端与齿轮轴5接触,且装配时保证其处于合适的压缩状态;齿轮轴5由两个圆柱滚子轴承4与9支承,可实现轴向移动;

由于碟簧处于适当的压缩状态,就会产生一个合适的预紧力对可以轴向移动的齿轮轴5施加一个轴向载荷F;基于碟簧一定条件下的变刚度特性,在齿轮轴5与斜齿轮6,及齿轮轴7与斜齿轮8两对斜齿轮副长时间工作同步磨损产生磨损间隙后,碟簧产生的轴向载荷F会呈非线性增大,推动齿轮轴5轴向移动,从而消除两对斜齿轮副产生的磨损间隙[3]27。

2 碟簧设计

2.1 碟簧选型设计

常见的碟簧分为:标准碟簧、开槽碟簧和膜片碟簧3大类[6]12-79。其中,膜片碟簧作为离合器专用碟簧,此处选型不予考虑。开槽碟簧是非标准件,其是在标准碟簧上沿直径方向上开出沟槽制成,所以其结构尺寸和标准碟簧一致。

综上所述,该设计的碟簧选型设计,在标准碟簧和开槽碟簧之间展开。

2.1.1 标准碟簧分析

单片标准碟簧的载荷位移曲线示意图如图2曲线1所示。

图2 碟簧载荷位移曲线示意图

图2中的曲线1,改变组合方式只能改变其平缓度,而不能改变其形状。

2.1.2 开槽碟簧分析

开槽碟簧是通过在标准碟簧上由内向外在直径方向上开出沟槽,从而形成悬臂片结构所制成,其结构如图3所示。

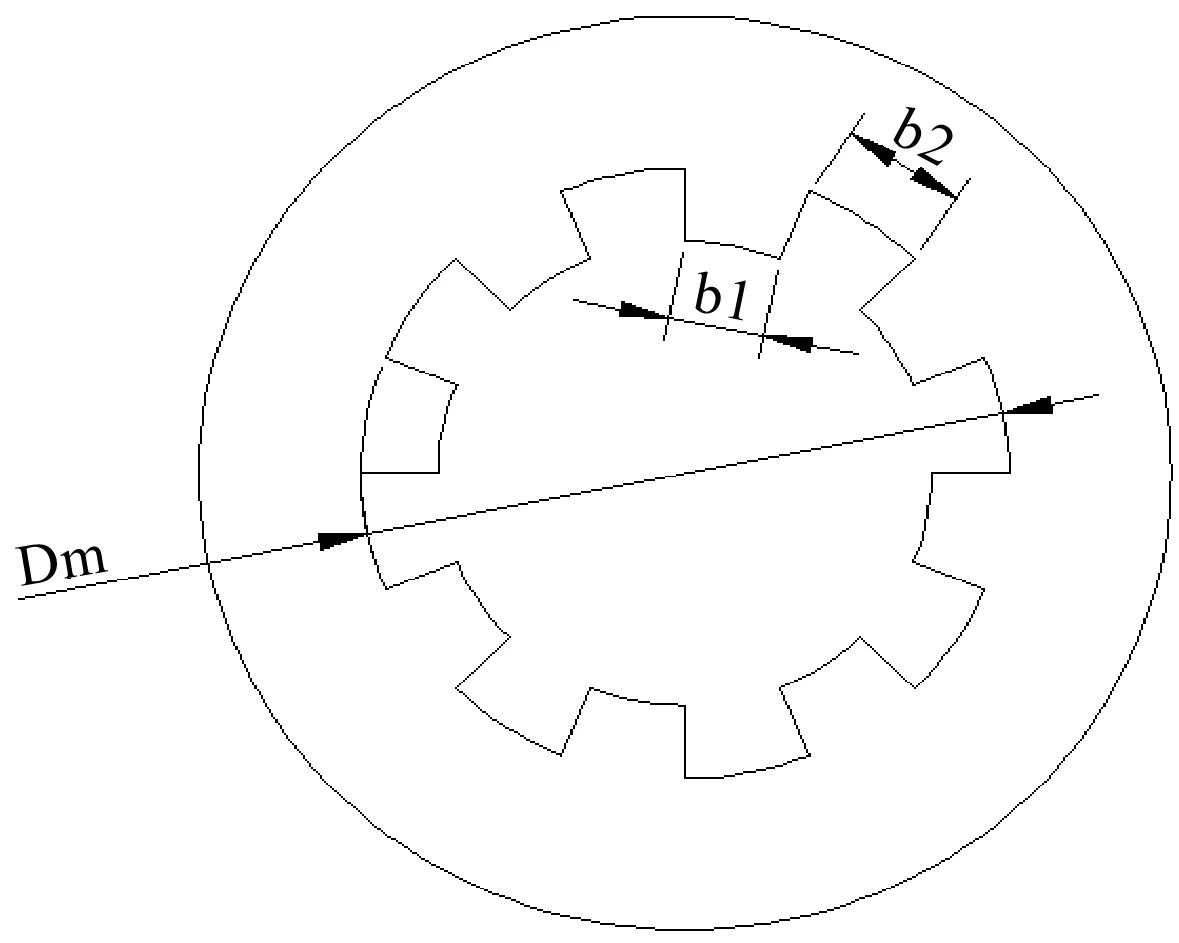
图3 开槽碟簧结构示意图

图3中,开槽碟簧结构兼具了蝶形弹簧和悬臂片弹簧的优点,根据开槽深度的不同,具有不同的渐减形载荷变形特征曲线,具体如图2的曲线2所示[7]。

2.1.3 碟簧的最终选型

由于碟簧自动补偿机构要求在一定范围内,碟簧载荷随位移的减小而增大,而开槽碟簧所具有的渐减形载荷-变形特征正好满足了设计要求,因此,笔者选定开槽碟簧作为碟簧自动补偿机构的核心部件。

2.2 非标开槽碟簧的理论设计

2.2.1 设计计算的初始条件确定

(1)假设条件如下[8]:

①碟簧承受载荷时,其矩形横截面只是围绕中性点转动,而不发生变形(即忽略径向力影响);

②碟簧材料呈线弹性,且各向同性;

③碟簧工作过程中忽略摩擦力影响;

④忽略碟簧热处理产生的内应力;

⑤碟簧所承受的载荷及支撑面所产生的反作用力为均匀载荷(沿内圆周到外圆周均匀分布)。

(2)碟簧受力分析及计算

由碟簧随动补偿磨损误差机构的工作原理及碟簧选型设计可得,对合碟簧是在一定的预压载荷作用下工作在碟簧的负刚度段,以实现对磨损误差的实时随动补偿的;此外,其仅受随工件或切削参数变化而跳跃性变化的轴向工作载荷作用,如图4所示。

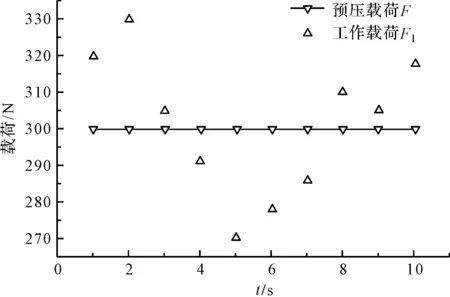
图4 碟簧工作载荷示意图

由新型转台参数可得：转台输出额定转速n=60 r/min、碟簧所在传动轴额定转速nII=195.3 r/min，转台额定输出功率Pw=8.5 kW，碟簧所在传动轴额定功率Pd=8.7 kW。

两斜齿轮的分度圆直径分别为:

根据新型转台参数可得:中间轴转矩T=90.66 Nm,中间轴转速n=195.3 r/min。

假设中间轴逆时针转动,对中间轴两齿轮受力分析,碟簧所在传动轴受力简图如图5所示。

图5 碟簧所在传动轴受力简图

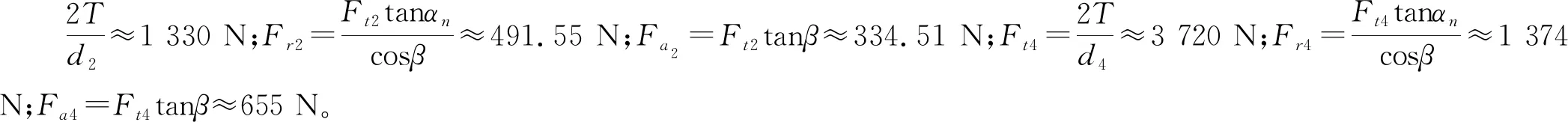
由上式计算,可推出碟簧承受的轴向载荷为:Fa=Fa4-Fa2=321 N。

2.2.2 开槽碟簧的基本参数计算

笔者参考《机械设计手册》,对开槽碟簧未确定的非核心参数确定如下[6]12-82:

标准规定开槽碟簧的舌片数Z=8,12,16,20。舌片数Z越多,则舌片与封闭环部分连接处的应力分布就越均匀;综合所选标准碟簧的尺寸,初选舌片数Z=8。

标准规定开槽碟簧的舌片根部半径R=0.5t,t,2t。该半径R越大则应力集中越小,综合考虑到碟簧的尺寸结构较小,故初选R=t=2 mm。

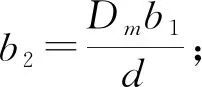
对于开槽碟簧而言,开槽中心圆直径Dm与外圆直径D的比值i是影响其渐减形载荷-变形特征曲线形状的核心因素;故对非标碟簧的设计的核心就是i值的确定[9]。

2.2.3 开槽碟簧位移载荷曲线的理论计算

开槽碟簧的变形由封闭环部分在直径Dm处的变形量f1与舌片变形量f2两部分组成。其中,f1与载荷P的关系为[10]:

(1)

式中:E—弹模量,E=20 600 MPa;μ—泊松比,μ=0.3;KI—系数,可从表中查找。

KI参考值如表1所示。

表1 KI参考值

f2与载荷P的关系为:

(2)

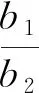
(3)

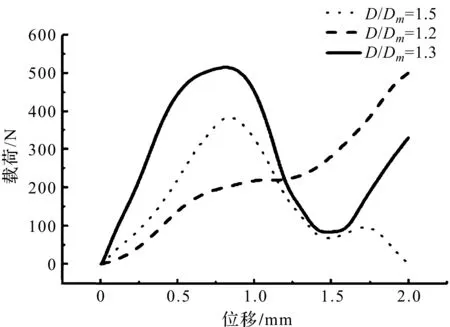
图6 理论计算位移载荷曲线

2.3 开槽碟簧位移载荷关系有限元分析校核

2.3.1 模型建立及网格划分

笔者根据开槽碟簧自动误差补偿机构的实际工况,借助UG建模工具箱建模,导入ANSYS显示动力学分析模块;并定义材料参数:泊松比μ=0.3,弹性模量E=206 000 MPa,屈服强度=1 600 MPa,密度Density=7 850 kg/m3;[11]同时,设置两圆环为刚体,碟簧组为柔性体。

划分的网格如图7所示。

图7 碟簧压缩模型的网格划分

2.3.2 求解设置及结果分析

在碟簧受力边上建立参考线L,仅释放Z向自由度,对上压板施加Z向速度V=0.25 mm/s,控制时间8 s,输出所受的力Fa,得到时间-载荷曲线如图8所示。

图8 时间载荷曲线

对应转换为载荷位移曲线如图9所示。

图9 =1.3的载荷位移曲线

继续分析Dm=21.17与Dm=16.93,并结合图9,可得到载荷位移曲线,如图10所示。

图10 ANSYS载荷位移曲线

该图与图6基本相符,由此从有限元分析的角度验证了理论计算的正确性。

3 非标开槽碟簧可靠性校核计算

3.1 开槽碟簧的强度校核计算

查机械设计手册可得,标准碟簧的载荷变形公式为[6]12-86:

(4)

当碟簧压平时，简化式(4)得碟簧所承受的外载荷为[12]:

(5)

式(4,5)中各计算系数可通过代入碟簧基本参数计算得到:

(6)

(7)

式(6,7)中,各计算系数可通过代入碟簧基本参数计算得到[13]:

(8)

(9)

(10)

3.2 开槽碟簧所受应力的校核计算

碟簧的应力类型分为拉应力和压应力两种,约定拉应力为正,而压应力为负[14],即:

(11)

(12)

(13)

(14)

(15)

上式中的参数计算如下:

(16)

(17)

3.3 开槽碟簧的刚度和变形校核计算

(18)

(19)

式中:d—内径;D—外径;t—厚度;E—弹性模量;μ—泊松比;K—刚度;H0—自由高度;P—外载荷;t′—有支撑面时的减薄厚度;h0—压平时的变形量;f—对应外载荷P的变形量;U—变形能[15]。

针对对合组合的碟簧组,没有固定的计算公式,只能根据选定的型号和系列进行经验性的估算考核,通常取值范围为单片碟簧的85%～95%[16]。

将选定的D=50、d=25.4及Dm=38.46的非标开槽碟簧参数(其余参数与标准碟簧相同)代入以上各中,通过计算可得安全系数S=1.34,即非标开槽碟簧的设计满足使用安全要求。

3.4 碟簧可靠性有限元分析校核

在2.3节ANSYS载荷位移特征曲线的基础上,取最大载荷F=525 N(t=0.75 s)时,安全系数云图及Z向应变云图如图11所示。

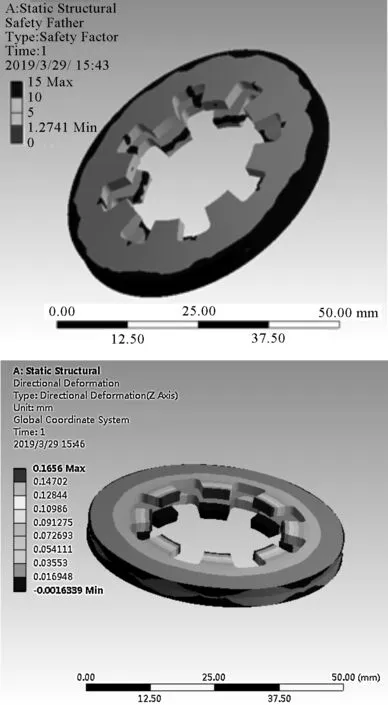
图11 安全系数云图及Z向应变云图

图11中,碟簧在最大压力Fmax=525 N时,安全系数S=1.27,与理论计算结果大致相符,即开槽碟簧满足设计工作要求。

4 开槽碟簧的模态分析校核

由于转台在工作过程中,叶片所受的切削力随切削参数的改变而不断改变,会产生100 Hz～3 000 Hz的高频振动。该高频振动的最大值如若高于碟簧的一阶固有频率,碟簧组则会在特定频率下产生共振,影响航发叶片的加工质量,故对碟簧进行预紧条件下的模态分析校核是必要的。

对有预紧的开槽碟簧进行模态分析,可得到开槽碟簧在预紧条件下的4阶固有频率及振型,并对开槽碟簧的设计合理性进行验证。

4.1 模态分析方案及边界条件确定

非标碟簧组模态分析的方案为静力学分析和模态分析相结合,先通过静力学分析给碟簧组施加一个适当的位移,以实现碟簧的预紧(预压载荷F=300 N),再导入其求解结果作为模态分析的初始条件进行分析,模态分析方案如图12所示。

图12 模态分析方案

笔者采用底部支承的固定约束,参考图10取预压位移S=0.9 mm,两碟簧的接触方式为绑定接触,分析4阶模态。

4.2 分析求解

经分析的各阶固有频率如表2所示。

表2 4阶固有频率

各阶模态的主俯视图如图13所示(自上而下依次为开槽碟簧的4阶模态的主振型图及俯振型图)。

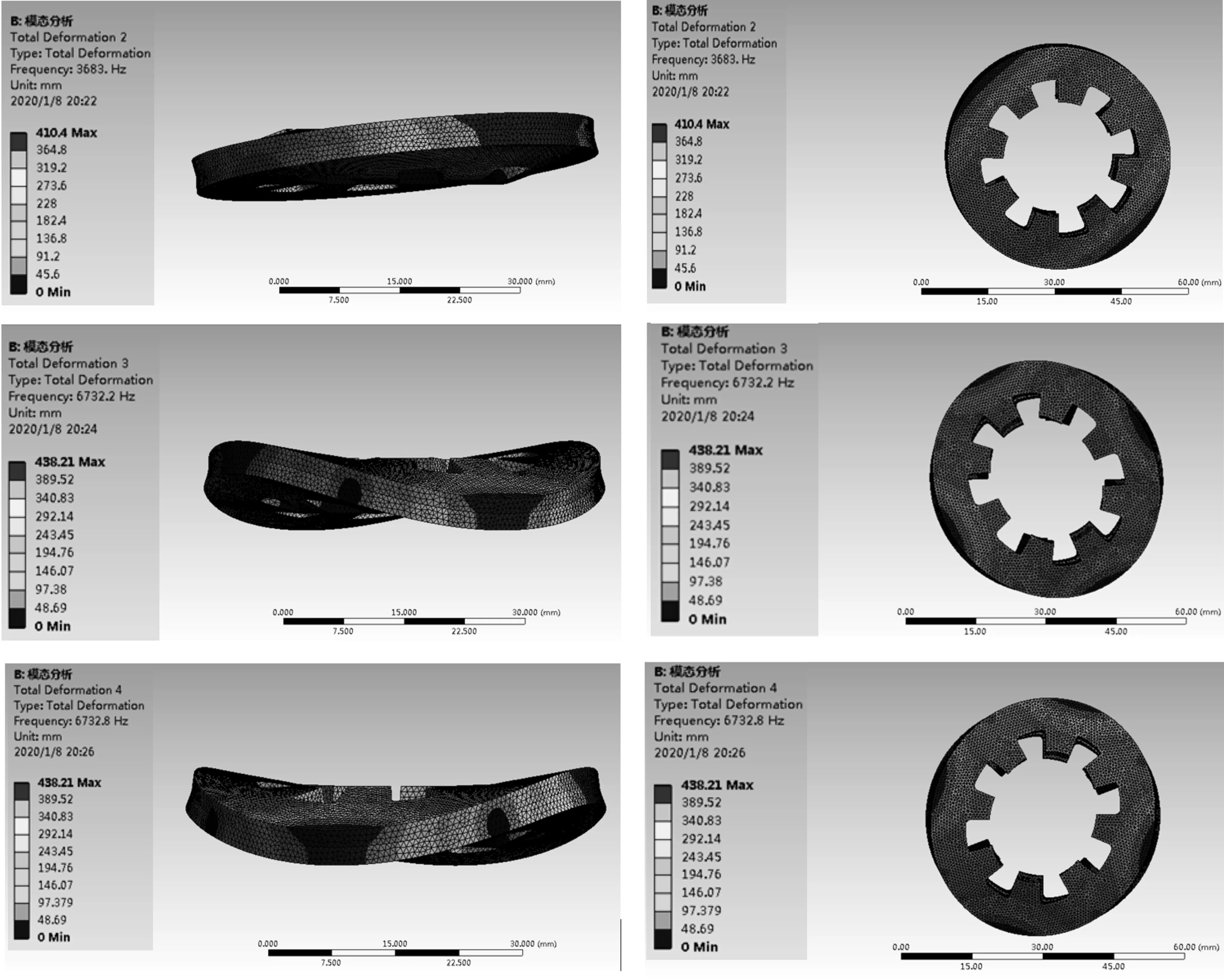
图13 开槽碟簧4阶模态振型图

从4阶固有频率表及振型图可得,开槽碟簧在转台的实际工况下,前2阶模态比较稳定且固有频率均大于3 000 Hz,能满足新型转台的使用要求。

5 实验验证

为了验证非标开槽碟簧组设计的正确性,笔者在利用线切割加工出非标开槽碟簧的基础上,利用拉压万能试验机,对非标开槽碟簧组进行了压缩试验;实验中,利用计算机编程以模拟碟簧组的实际工作条件,直接得到了开槽碟簧组的载荷-位移特性曲线;一方面检测其是否满足设计要求,另一方面间接检测非标开槽碟簧设计计算理论的正确性。

试验设备及平台搭建如图14所示。

图14 实验设备及平台搭建

由拉压万能试验机控制计算机输出的载荷位移曲线,如图15所示。

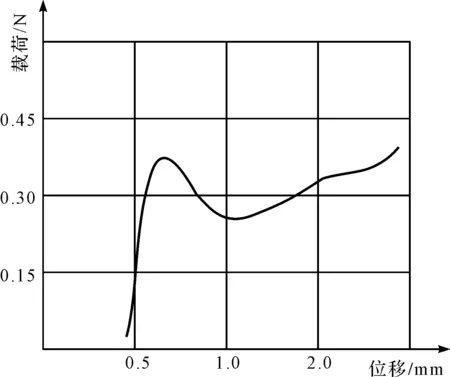
图15 试验所得载荷位移曲线

图15与图6、图10基本契合,均以300 N为对称中心,且有最优异的渐减性载荷位移特性曲线(压缩位移为0.7 mm～1.1 mm段),由此最终验证了非标开槽碟簧的设计满足设计要求,及非标开槽碟簧理论计算设计体系的正确性。

6 结束语

本文设计了一种非标开槽碟簧随动补偿磨损误差机构,利用非标开槽碟簧优异的变刚度及渐减性位移-载荷特性曲线两大特性,实现了对磨损误差的实时随动补偿,达到了提高转台精度稳定性和寿命,满足了航发叶片的加工要求。

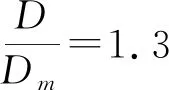
本文提出了以更具变刚度特性的非标开槽碟簧取代标准碟簧的构想,并完成全套理论设计计算和验证。