基于辛几何提取变换的轴承故障诊断研究*

赵 杰,陈志刚,2*,王衍学,柴 龙,高 山

(1.北京建筑大学 机电与车辆工程学院,北京 100044;2.北京市建筑安全监测工程技术研究中心,北京 100044; 3.中国石油集团川庆钻探工程有限公司 长庆井下技术作业公司,陕西 西安 710021; 4.海洋石油工程股份有限公司, 天津 300452)

0 引 言

轴承是旋转机械设备的核心部件之一,其工作状态的好坏直接影响到整个设备的性能及安全[1]。由于轴承运行过程中振动数据驳杂,常常充斥着各种噪声,造成故障特征难以提取。目前,许多相关研究取得了显著进展,但是对于非平稳信号噪声处理和特征提取方面仍有很多问题没有解决。

时频分析方法(TFA)可以揭示非平稳信号的动态特性,是处理非平稳信号时变特征非常有效的工具[2]。近年来,TFA在工程应用中发挥了重要的作用。经典的TFA方法包括短时傅里叶变换(short-time Fourier transform,STFT)、小波变换(wavelet transform,WT)、Wigner-Ville分布等[3]。然而,由于Heisenberg测不准原理和交叉干扰项的限制,传统的方法存在TF分辨率低的问题,无法准确表征非平稳信号的非线性行为。小波变换将信号分解为多个分量[4],呈现出不同的信号特征,可以在时-频域挖掘信号的局部微弱信号特征[5],但是其不足之处在于WT是一种基于可调窗口的STFT,所以存在模态混叠的问题,并且小波基的选择受人为影响较大,对于不同信号的适应性差。

经验模态分解(empirical mode decomposition,EMD)是一种自适应的信号分解方法[6],可以将信号分解为几个固有模态分量(intrinsic mode function,IMF),不需要输入任何参数,通过迭代和极值点包络对信号进行分解,避免了WT人为输入小波基带来的影响,但是也存在模态混叠等不足。李国华等人[7]和TORRES等人[8]在EMD的基础上又提出了集合EMD和互补集合EMD,加入了随机白噪声进行模态分解,以中和信号中的噪声,在一定程度上抑制了信号的模态混叠现象;但是其不足之处在于无法完全消除添加的随机白噪声,以及迭代次数过高,导致计算量大、运算缓慢等问题存在。

变分模态分解[9,10](variational mode decomposition,VMD)通过约束变化代替迭代包络,分解为多个IMF,适用于复杂信号;但是其参数设置仍然受人为经验因素的影响。PAN Hai-yang等人[11]在辛几何谱分析的基础上提出了辛几何模态分解(symplectic geometry mode decomposition,SGMD),利用辛几何相似变换计算了轨迹矩阵的特征值和特征向量,并通过对角平均得到了相应的初始辛几何分量;其分解效果虽然较好,但是特征提取却不太理想。

同步挤压变换(synchro squeezing transform,SST)是一种后处理工具,能够挤压或重新分配TF系数[12]。在此基础上还衍生了许多TF方法,如解调SST[13]、高阶SST[14],都在TF能量聚集性上进行了加强,但是都存在能量发散的问题。YU G等人[15]发现了原始STFT结果在某些特定位置可以取最大的值,因此提出了一种具有良好噪声鲁棒性的TFA方法,称为同步提取变换(synchronous extraction transformation,SET),使用同步提取算子(SEO)提取TF脊线上的TF系数,减少了TF能量发散,使TF图像更加清晰;但是由于核函数限制,对于复杂瞬变信号该方法还不能有效提取。

本文针对以上不足,提出一种基于辛几何特征提取的时频分析方法,首先对故障信号进行辛几何分解处理,利用峭度准则[16]筛选出最相关分量,然后引入提取算子(SEO)进行特征提取,最后通过仿真与实验对该方法的有效性和适用性进行验证,并将其与多种经典方法进行比较。

1 辛几何算法

对于任意的时间序列x={x1,x2,…,xN}(其中:N—时间序列x的长度),那么可以构造一个轨迹矩阵:

(1)

式中:k—嵌入维数;τ—延迟时间;

其中:m=N-(k-1)τ。

通过选择合适的嵌入维数k和延迟时间τ,可以得到相应的轨迹矩阵;可以利用功率谱密度(PSD)对嵌入维数k自适应确定,然后通过计算定义PSD中最高峰值所对应的频率为fmax,设Fs为采样频率。若归一化频率小于给定的阈值0.001时,取d=n/3，否则d=1.2×(Fs/fmax)。对X进行自相关分析,可得到协方差对称矩阵A:

A=XTX

(2)

然后根据协方差矩阵A构造Hamilton矩阵M：

(3)

由Hamilton矩阵的定义可知N=M2，也为Hamilton矩阵，所以构造正交辛矩阵Q为：

(4)

式(4)中，由正交辛矩阵Q的性质可知，在进行辛变换时，可保护Hamilton矩阵的结构不被破坏，保留其特征(B—上三角矩阵)。

将矩阵B通过Schmidt正交化变换为矩阵N，得到B的特征值λ1，λ2，λ3，…λn,。由Hamilton矩阵的性质可知，矩阵A的特征值为：

(5)

则X的辛几何为：

σ1>σ2>…>σd

(6)

Z=Z1+Z2+…+Zd

(7)

对任意的初始单分量成分Zi，定义Zi中的元素为zij，1≤i≤d，1≤j≤m；且d*=min(m,d),m*=max(m,d),n=m+(d-1)τ，令:

(8)

那么对角平均矩阵yk为：

(9)

由式(9)可求得一组长度为n的一维序列Yi，并与重构矩阵Zi对应，进而通过上述步骤可得到d个具有不同趋势项和不同频带的独立分量SGC(symplectic geometry component)：

Y=Y1+Y2+…+Yd

(10)

由于环境噪声复杂，通常夹杂着不同来源的噪声信号，需要设置迭代停止条件。首先计算初始单分量的相关性，高度相关的组成第一个SGC分量，并从原信号去除，剩余信号为：

(11)

式中：h—迭代次数。

最后计算剩余项和原信号的归一化方差NMAE：

(12)

当归一化方差等于给定阈值，即NMAEh=1%时，迭代过程结束，否则持续分解到符合阈值条件，最终结果为：

(13)

2 同步提取变换

由于同步提取变换是基于STFT的后处理过程,首先分析STFT,其表达式为:

(14)

式中：g(u-t)—可移动窗口；s(u)—待分析信号。

STFT将一维时间信号s(u)扩展到二维Fourier平面，从而可以观察提取信号的时频域信息。对STFT乘相位因子eiωu，根据Parseval定理，式(14)可以写成：

(15)

取一个频率ω=ω0，振幅恒为A的谐波信号为：s(t)=A·eiω0t，那么其频域表现形式为：

(16)

由式(15)可得s(t)的STFT为：

(17)

根据式(17)可以得出:谐波信号的STFT表示是由与原信号具有相同频率ω0的一系列谐波信号组成，原始的TF表示|Ge(t,ω)|在IF轨迹上达到最大值，时频系数Ge(t,ω)将会具有最好的噪声鲁棒性。

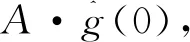
(18)

式中：∂tGe(t,ω)—Ge(t,ω)对时间t的偏导数。

那么STFT在瞬时频率位置的TF系数即可进行提取，即同步提取变换SET：

Te(t,ω)=Ge(t,ω)·δ(ω-ω0(t,ω))

(19)

式中：δ(ω-ω0(t,ω))—提取算子SEO，通过SEO可提取保留能量较大的系数，剔发散系数。

3 仿真分析

为验证所提方法对于多分量信号进行特征提取时的抗混叠能力,及其时频能量聚集性,笔者采用蝙蝠信号进行时频分析。

仿真信号为经典的蝙蝠回声定位信号,时域波形如图1所示(由一个大棕蝙蝠发出)。

图1 蝙蝠信号

笔者采用经典的4种TFA方法:STFT、SST、DTFA、SET对图1信号进行特征分析提取,4种方法TF表示及局部放大如图2所示。

图2 4种方法TF表示及局部放大

图2(a,c,e,g)分别为STFT、DTFA、SST、SET的TF分析结果,图2(b,d,f,h)分别为4种分析方法的局部放大图,在图2中用箭头连接,一一对应。

从图2中可以看出:前两种方法由于DTFA采用非线性TF基函数,能量集中效果比STFT好,但是由于Heisenberg测不准原理,DTFA的TF表示仍然是发散的;

SST在频率方向上对TF系数进行挤压,达到了能量集中的效果;SET利用SEO算子剔除发散TF系数,保留脊线上的TF系数,实现了TF能量集中,效果比SST好。

能量聚集程度越高,越能较好地定位信号的位置,且清楚地表征信号的时变特征。Renyi熵是信息熵的一种,是评价能量浓度的客观指标,其数值越低表示能量聚集性越好。

笔者计算了4种方法的Renyi熵,如表1所示。

表1 4种方法Renyi熵

由表现可以看出,SET数值最低,能量聚集性最好。

4 实验验证

4.1 数据采集

数据采集装置选用实验室搭建的轴承故障诊断实验台。试验台包括交流电动机、电机速度控制中心、支撑轴、测试轴承、磁粉制动器,扭矩传感器等,数据采集传感器选用美国PCB公司的622B01型ICP传感器。

测试轴承为6105-SKF深沟球轴承,通过电火花加工的方式在轴承外圈和内圈刻蚀直径0.155 mm、深度0.287 mm的裂痕,模拟轴承运行过程中外圈和内圈产生的故障。

试验台与实验故障轴承如图3所示。

图3 试验台与实验故障轴承

采样频率设置为12 kHz,转速1 750 r/min。

外圈的故障频率为:

(20)

内圈的故障频率为：

(21)

式中：r—转速；n—滚珠个数；d—滚动体直径；D—轴承节径；α—滚动体接触角。

由式(20,21)可分别计算出外圈、内圈的故障频率为104.5 Hz、156.4 Hz。

为验证所提方法的适用性和准确性,笔者选用轴承外圈和内圈数据进行比较分析。

4.2 外圈故障分析

轴承外圈传感器放置在轴承3点钟方向进行数据采集。笔者首先利用辛几何算法对信号进行分解,得到5个sgc分量,如图4所示。

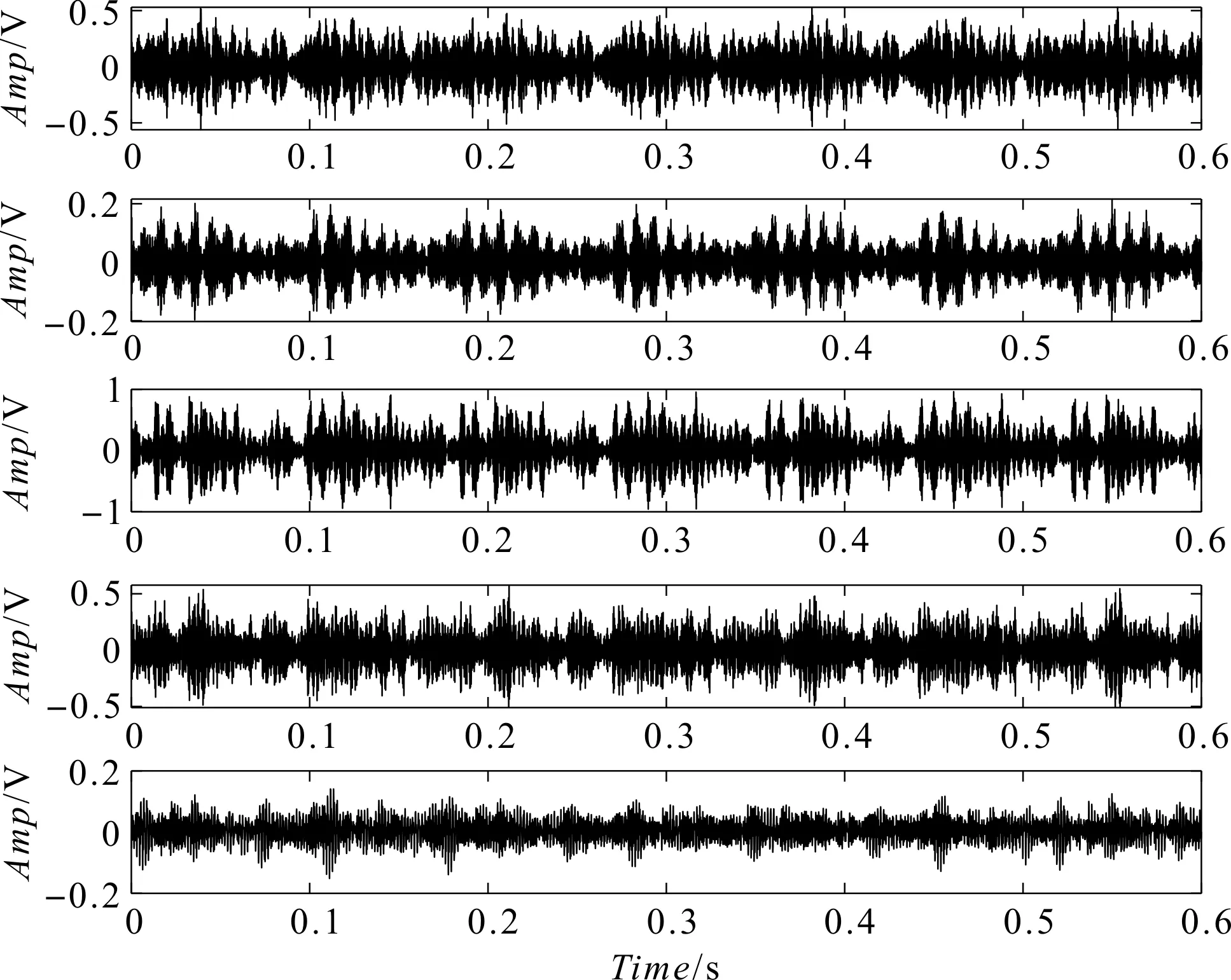
图4 sgc分量

然后计算5个sgc的峭度,并选取最接近的3个sgc进行重构,达到降噪的效果,sgc的峭度值和重构信号如图5所示。

图5 sgc的峭度值和重构信号

从图5中可以看出,重构信号相比于原始信号降噪效果良好。

笔者选取比较经典的4种TFA方法:STFT、SST、DTFA、SET进行对比分析,TF结果如图6所示(右侧为局部放大)。

图6 TF结果

图6中,STFT和DTFA方法效果模糊,TF能量严重分散;SST虽然把TF能量进行挤压,但是效果仍然不佳有一定的发散现象;SET能够把时频脊线上能量进行剔除,可以提取出清晰的TF能量。

4种方法的Renyi熵如表2所示(SET的Renyi熵最低,TF能量更加聚集)。

表2 外圈信号Renyi熵

最后,笔者将提取的TF分量做Hilbert包络谱分析,如图7所示。

图7 TF分量包络谱

根据图7可以看出，信号的故障频率f0及其2倍、3倍、5倍、6倍频率,效果较好。

4.3 内圈故障分析

由于内圈信号通常比较复杂,笔者对其重点分析。首先对其做辛几何算法分解,得到7个sgc分量,如图8所示。

图8 sgc分量

然后笔者分别计算其峭度值,并选取相关度最高的第1、2、5个分量进行重构,如图9所示。

图9 sgc分量的峭度值和重构信号

图9展示了原始信号和重构信号的对比,可以看出,通过重构滤除了大部分噪声,时域图像更加清晰。

笔者使用4种经典TFA方法STFT、SST、DTFA、SET进行对比分析,TF分析结果如图10所示。

图10 TF分析结果

图10中,DTFA方法TF能量发散最为严重,STFT次之;SST方法部分能量压缩较好,但仍有位置存在能量发散现象;SET方法将TF脊线附近的能量进行滤除,只保留中心能量,脊线清晰,不存在能量发散现象。

4种方法的Renyi熵如表3所示。

表3 内圈信号Renyi熵

由表3中数据可知,SET数值最低,能量聚集性高。

笔者对4种方法所提取的TF分量做Hilbert包络谱分析,如图11所示。

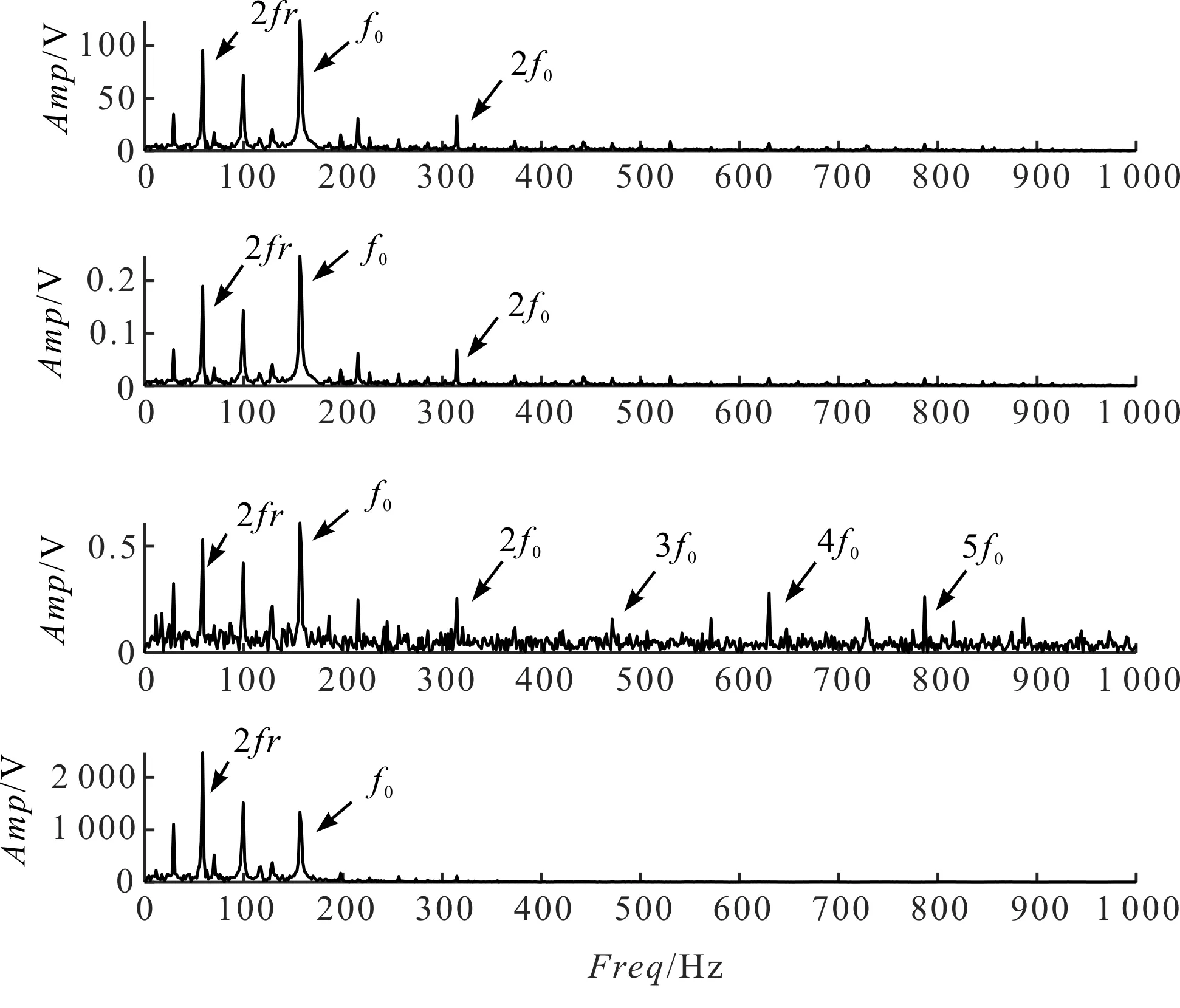
图11 Hilbert包络谱分析

从图11可以看出:4种方法皆能表示出轴承的转频fr及其倍频,然而对于故障频率f0,由于Heisenberg测不准原理的限制,基于Fourier变换的STFT和DTFA无法提供清晰的TF表示,导致其包络谱所示故障信息较少;SST在对TF系数进行挤压的同时,由于受到调频噪声的影响,TF能量发生了分散,仍无法清晰展现故障多倍频率,只有SET方法提取的TF系数较为明显,能量聚集性高,可以清楚地表示f0及其多倍频率。

5 结束语

本文提出了一种基于辛几何提取算法的轴承故障诊断方法,首先对故障信号进行了辛几何分解处理,利用峭度准则筛选出最相关分量,然后引入提取算子(SEO)进行了特征提取,最后通过仿真与实验对该方法的有效性和适用性进行了验证,并将其与多种经典方法进行了比较。

主要研究结论如下:

(1)利用辛几何算法分解轴承故障振动信号,有效避免了模态混叠,并利用峭度准则挑选相关分量进行重构,滤除了大部分噪声分量,鲁棒性较好;

(2)利用提取算子(SEO)把信号发散能量剔除,仅保留时频脊线的中心能量,使得能量聚集性更高,易于分析;

(3)结合辛几何算法噪声鲁棒性强的优点,将SEO引入其后续步骤,为TF分析奠定了良好的基础,使其更易于分析非线性非平稳的轴承振动信号。

另外,对于辛几何算法终止条件的优化问题,还有待于后续的研究。