基于TET瞬态特征提取的滚动轴承早期故障诊断研究*
陈志刚,赵 杰,张 楠,车昊阳
(1.北京建筑大学 机电与车辆工程学院,北京 100044;2.北京市建筑安全监测工程技术研究中心, 北京 100044;3.中国石油集团川庆钻探工程有限公司 长庆井下技术作业公司,陕西 西安 710021)
0 引 言
旋转机械设备运行环境复杂多变,滚动轴承作为其重要部件,在其中发挥着不可或缺的作用。旋转机械设备一旦发生事故,将会造成巨大经济损失和员工伤亡,所以对轴承进行必要的故障诊断意义重大[1]。
旋转机械设备运转过程中通常夹杂着来自不同振源的噪声,使得瞬态故障振动信号难以被提取、识别,不能被有效地诊断和分析。
在实验采集到的振动信号中,通常夹杂着短时间的瞬变特征,而早期微弱故障往往发生在信号瞬变的时刻,在强噪声背景下的特征提取困难,不易识别,所以研究高效的时频分析方法尤为重要[2]。
时频分析(TFA)方法对于时变信号十分有效,在过去的几十年里受到了业界极大的关注,其自身也得到了长足的发展。但是,传统的TFA技术依然存在较大的问题,如信号两边的交叉项干扰、分解模态混叠、海森伯格不确定性原理等问题。
短时傅立叶变换[3](short-time Fourier transform, STFT)的时-频分辨率较好,但对于不同的信号适应性较差,需重新选择窗函数;小波变换[4](wavelet transform,WT)的窗口大小可根据信号频率的不同做出改变,克服了STFT的缺点,但是小波基的选择受人为影响较大;Wigner-Ville[5]分布具有较高的时频分辨率,对于多分量信号存在交叉干扰项,分析效果较差。
经验模态分解(empirical mode decomposition, EMD)是HUANG N E[6]在1998年提出的一种自适应时频信号处理方法。该方法对于非线性、非平稳的信号的处理效果较好,解决了WT人为选择小波基函数的问题;但是该方法也存在端点延拓[7]、模态混叠的问题[8]。
为了改善EMD的缺点,聚合经验模态分解[9](ensemble empirical mode decomposition, EEMD)被提了出来。该方法在分解过程中加入随机白噪声,这使得模态的混叠问题在一定程度上得到了一些改善,但端点效应问题仍然存在。
在总结了以上问题的基础上,TORRES M E[10]在EMD、EEMD的基础上,提出了一种自适应噪声完备集合模态分解(CEEMDAN)。该方法具有更好的收敛性,且重构误差基本为0,重构后具有良好的降噪效果。
瞬态提取变换[11]是一种比较新的TFA方法。该方法的分辨率较高,能够较好地提取出故障的瞬态特征。
笔者进行了大量文献调研,发现目前基于TET的轴承瞬态故障诊断研究较少。因此,本文提出了一种瞬态特征提取的轴承故障诊断处理方法。首先,通过CEEMDAN对原始信号做自适应降噪;然后,将重构的信号利用瞬态特征提取算子(transient extraction operator,TEO)提取瞬态特征;最后,利用仿真信号和实验室轴承故障试验台信号比较,对比STFT、同步挤压变换(synchro squeezing transform,SST)、重分配法(reassignment method,RS)、解调TFA(demodulated TFA,DTFA)等方法。
1 自适应噪声集合模态分解算法
自适应噪声集合模态分解(CEEMDAN)是在EMD、EEMD的基础上改进得到的[12]。首先,该方法是将信号分解为一个模态分量IMF;然后,进行总体平均计算,得到第一阶IMF;最后,对剩余分量进行上述操作。该方法有效地减小了模态混叠效应和噪声的遗留问题。
该算法具体步骤如下:

(1)

(2)
将r1(t)作为输入信号,重复以上步骤,即可得到第K个模态分量IMFk(设总共有K个模态分量),最终剩余信号为R(t),则原始信号x(t)可得到K个IMF和一个R(t),即:
(3)
采用仿真信号可以验证CEEMDAN的降噪效果。由于轴承运行过程中,原始信号中通常会具有调频调幅成分,此处设仿真信号f(t)为:
(4)
式中:f1(t)—余弦信号;f2(t),f3(t)—调频信号;f4(t)—随机白噪声,采样频率设置1 kHz。
选用其中1 s的数据,通过CEEMDAN进行模态分解,可以得到9个模态分量IMF,如图1所示。

图1 CEEMDAN分解结果
然后,分别计算9个IMF的峭度值[13,14],如图2所示。

图2 IMF峭度
由图2可以看出:第2、3、4个模态的峭度值较大,相关度较高;因此,此处选其进行重构。
信号的预处理如图3所示。

图3 信号预处理
图3中,重构降噪之后的信号如图3(b)所示。跟图3(a)中的原始加噪信号相比,重构降噪之后的信号滤除了部分噪声,效果较好。
2 瞬态提取算法
由于该方法是基于短时傅里叶变化(STFT),不需扩展参数和先验信息[11]。STFT表达式为:
(5)
式中:g(u-t)—可移动窗口;s(u)—输入信号。
t0=0.5 s时,δ(t)的时频谱如图4所示。

图4 t0=0.5 s时的时频谱
在数学上,δ(t)函数是一个冲击函数,在零点处的值无限大,非零处的值为零,且积分为1。此处令A=1,t0=0.5,则时域和频域图像如图4(a,b)所示。由此,将其看作具有瞬态特征信号的理想模型。
δ(t)通常可表示为:
sδ(t)=A·δ(t-t0)
(6)
由于STFT的局限性,又根据海森堡(Heisenberg)测不准原理,即使是δ(t)函数也不可能实现理想描述,为了探究STFT对δ(t)的时频能量分布,笔者将式(6)代入式(5),可得:
A·g(t0-t)·e-iωt0
(7)
因为|e-iωt0|=1,δ(t)的STFT能量分布可以表示为:
|G(t,ω)|=A·g(t0-t)
(8)
由式(8)可以看出:窗口函数g(t)在时域是紧凑的,频域能量主要分布在t0时刻,并达到最大值A·g(0)。
一个δ(t)函数的STFT由一系列具有相同群延迟(group delay, GD)的δ(t)函数构成,通过计算G(t,ω)相对于频率变量的导数,可以得到精确GDs,即:
∂ωG(t,ω)=∂ω(A·g(t0-t)·e-iωt0)=
-it0·A·g(t0-t)·e-iωt0=
-it0·G(t,ω)
(9)
对于任意的(t,ω),若G(t,ω)≠0,那么二维GDt0(t,ω)可以定义为:
(10)
群延迟GD和提取算子TEO如图5所示。
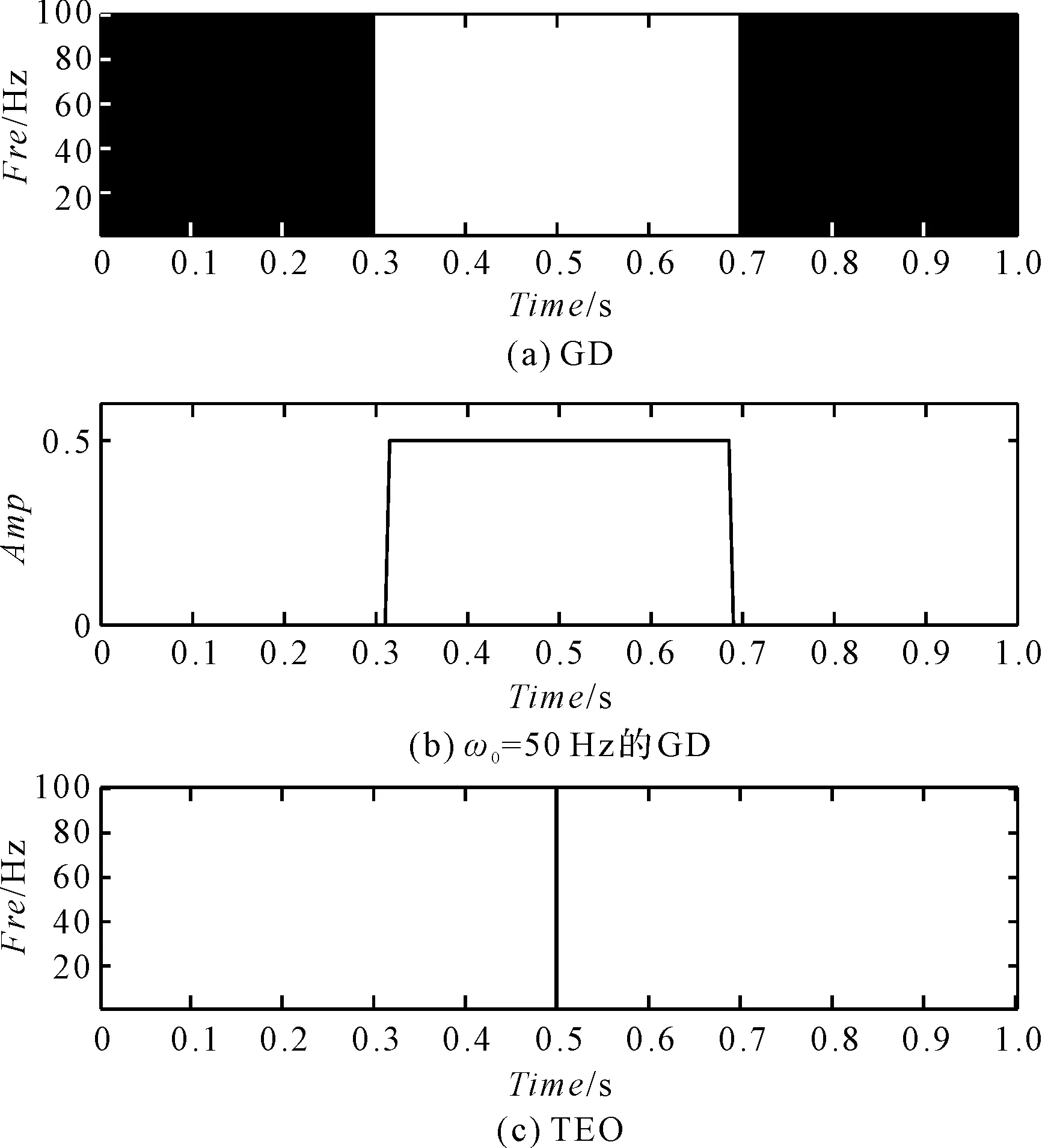
图5 群延迟GD和提取算子TEO
为了更清楚地说明GD,图5(b)为ω0=50 Hz时GD的频率片段。
在t∈[t-Δ,t+Δ](Δ为时间偏移)时刻,所有二维GD的值都与t0=0.5 s时刻的值相同。对于理想的TFA方法,信号的能量应该只出现在t0时刻,而不是在一定的范围内发生扩散。
为了消除这一能量扩散带来的影响,笔者只保留t0时刻的能量,提出了一种瞬态提取算子(TEO)的TFA方法:
TEO(t,ω)=δ(t-t0(t,ω))
(11)
由此可得:
(12)
则:
δ(t-t0(t,ω))=δ(t-t0)
(13)
由式(13)可以看出:TEO的值只有在t=t0时才可以提取时频系数G(t,ω),如图5(c)所示。
因为式(11)具有瞬态提取行为,笔者采用瞬态提取算子(TEO)的变换称为瞬态提取变换(TET),即:
Te(t,ω)=G(t,ω)·TEO(t,ω)
(14)
实际诊断中,仅对信号做频域处理往往是不够的,有时还需要得到信号的时域信息。
由STFT信号重构表达式:
(15)
很容易可以得出TET重构表达式:
(16)
3 仿真分析
为验证笔者所提方法的瞬态特征提取效果,此处采用瞬变仿真信号进行分析验证。
仿真信号如图6所示。

图6 仿真信号
为了衡量不同方法的处理效果,笔者采用Renyi熵来估计信号的分散程度[15]。Renyi熵也是信息熵的一种,可以表示为:
(17)
在图6的仿真信号中,加入信噪比1 dB~30 dB的高斯白噪声,采用短时傅里叶变换(STFT)、瞬态提取变换(TET)、小波变换(WT)、同步挤压变换(SST)、重分配变换(RS)、离散函数分析(DTFA)来对其加噪信号进行分析处理。其中,TF结果的Renyi熵越低,表示该方法的效果越好,能产生更加集中的TF表示。
在信噪比1 dB~30 dB时,6种方法TF结果的Renyi熵水平如图7所示。

图7 6种方法在信噪比1 dB~30 dB时TF结果的Renyi熵水平
由图7可以看出:在不同噪声水平下,TET的效果最好。
笔者选取Renyi熵较低的4种方法,即STFT、SST、RS、TET,查看其TF表示。4种方法的TF表示及其局部放大结果如图8所示。

图8 4种方法TF表示及局部放大
由图8可知:STFT、SST、RS的TF表示结果比较分散;而TET结果能量集中,没有发散现象,效果较好。
4 实验验证
4.1 信号采集
笔者采用实验室轴承试验台进行数据采集。试验台由交流电动机、电机速度控制中心、支撑轴、测试轴承、传感器等组成。
传感器选用美国PCB公司的352C33型ICP加速的传感器,测试轴承为6105-SKF深沟球轴承,通过电火花加工的方式在轴承外圈和内圈刻蚀直径0.144 mm、深度0.232 mm的微小裂痕,模拟轴承运行过程中外圈和内圈产生的早期微弱故障。
轴承实验台及其部件如图9所示。

图9 实验台及其部件
图9中,采样频率Fs=12 kHz,转速1 750 r/min。根据式(18,19),可计算出外圈和内圈故障特征频率为104.5 Hz和157.9 Hz。
轴承外圈特征频率为:
(18)
内圈特征频率为:
(19)
式中:r—转速;n—滚珠个数;d—滚动体直径;D—轴承节径;α—滚动体接触角。
4.2 轴承外圈信号分析
轴承外圈信号的预处理如图10所示。

图10 外圈信号预处理
图10中,笔者首先对外圈信号进行处理,以展现轴承外圈的原始振动信号;传感器在3点钟方向采集。可以看到,瞬变信号完全被噪声淹没,无法清晰地观察;
然后对信号进行CEEMDAN分解,并计算各个模态分量IMF的峭度值,共有11个IMF分量,其中,第1、2、4个IMF峭度值较大,与原信号相关度较高,选其进行重构。可以看出,经过重构之后,滤除了大部分噪声,能够清晰地看到故障的瞬变特征。
笔者选用第3节中效果较好的4种方法(STFT、SST、RS、TET)对降噪信号进行处理,并生成TF表示,如图11所示。

图11 4种方法TF表示及局部放大
由图11可以看出:STFT结果比较发散,无法准确定位;RS和SST只提供了较为粗略的TF表示,依旧不能定位TF信息;TET则表现出了比较清晰的TF结果,效果较好。
瞬态特征分量如图12所示。
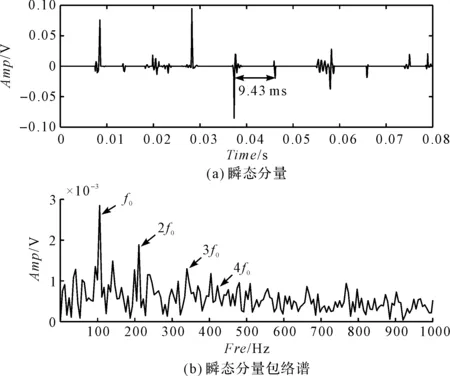
图12 瞬态特征分量
图12中,相比于降噪后的信号(图10(c)),提取TET的结果(图12(a))的瞬变特征有了明显改善;
图12(a)的相邻瞬变信号的间隔为9.5 ms,对其做Hilbert包络谱分析后,可以清晰地观察到故障频率f0及其2倍、3倍、4倍频率,可见其效果较好。
4.3 轴承内圈信号分析
由于轴承内圈、外圈的故障机理具有一定的差异性,来自外圈和滚动体的振动噪声与内圈本身的噪声相叠加,会导致其故障特征更加难以识别[16]。为了验证本文所提方法的适用性,笔者对内圈故障信号进行分析。
轴承内圈的信号预处理如图13所示。

图13 内圈信号预处理
图13中,笔者首先采用与处理外圈信号相同的方法,对内圈故障信号进行了自适应降噪处理,用CEEMDAN方法对其进行了分解,通过调整CEEMDAN信噪比及迭代次数,得到了11个IMF分量,并计算了每个分量的峭度值。
由图13(b)可知:第1、2、11分量峭度值较大,说明与原信号相关度较高;剩余分量则为噪声分量,通过重构1、2、11分量达到降噪的目的,如图13(c)所示。与原信号相比,其效果较好,滤除了大部分的噪声。
然后,笔者对降噪后的信号采用4种方法(STFT、SST、RS、TET)进行了对比分析,并计算了每种方法的Renyi熵,如表1所示。

表1 STFT、SST、RS、TET的Renyi熵
由表1可以看出:RS方法的Renyi熵数值最大,TET的数值最小,这说明了TET的效果最好。
4种方法的TF表示如图14所示。

图14 4种方法的TF表示
图14中的结果表明:STFT的TF结果能量发散最为严重,无法准确定位;SST结果能量受Heisenberg不确定性原理的影响也比较发散;RS结果相对较好,但还是没有TET结果更清晰、准确。
最后,笔者提取了TET结果的TF分量,其瞬态特征分量分析结果如图15所示。

图15 瞬态特征分量
由图15可以看出:图15(a)中的瞬变信号非常明显,分量的间隔基本为6.3 ms,与故障频率157.9 Hz相对应;对瞬态分量在Hilbert进行包络谱分析,可以在图中清楚地观察到内圈信号的故障特征频率f0及其2、3、4、5倍频,可见其效果很好。
5 结束语
本文提出了一种瞬态特征提取的轴承早期故障诊断方法,能够有效地对故障信号自适应进行滤波降噪,并提取出了轴承故障瞬态特征,结果表明其抗噪性较强,效果也较为明显。
主要结论如下:
(1)利用CEEMDAN对仿真信号及实验信号进行了自适应分解,并通过峭度选择相关度较大的分量重构降噪,实测数据表明其效果较好,噪声的鲁棒性较强;
(2)对降噪之后的信号进行了瞬变信号特征提取,然后做Hilbert包络谱分析,能够容易地找到轴承故障特征频率及其多倍频,并且选取轴承的外圈和内圈进行了分析对比,结果表明其皆可以有效地分析出其故障频率,这说明了该方法的适应性较强;
(3)将该方法与STFT、SST、RS、TET等方法作了比较分析,结果表明TET优于其他先进TF方法,且TET基于STFT,运算量相当,可以将其应用于实际中的轴承早期微弱故障诊断之中。
另外,对于CEEMDAN分量的选择问题,还有待于在后续的研究中进一步进行优化,使其与原信号的相关度更高。

