基于改进量子遗传算法的重型装备生产调度研究*

张 琪,杨晓英

(河南科技大学 机电工程学院,河南 洛阳 471003)

0 引 言

重型装备是典型的单件离散型产品,部件关联性强,加工与装配具有很强的并行性。传统的机械作业车间调度(job-shop scheduling problem,JSSP)通常把零件加工与产品装配分开,主要针对纯加工或纯装配调度进行研究,难以应对产品内在加工与装配的并行处理关系。综合作业调度(CJSSP)是具有实际应用背景的生产调度问题,充分考虑产品加工与装配的并行性,将分阶段调度模型转化为产品制造链调度[1]。因此,对重型装备综合作业调度问题进行深入研究具有重要意义。

CJSSP研究对象主要为大型复杂产品,其生产调度要遵循严格的装配顺序约束,一般以单个产品最小生产周期为优化目标[2-4]。多产品综合作业调度方面,梁艳杰等[5]的研究以多个产品总完工时间最小为优化目标,未能体现不同产品对交货期需求的差异性。谢志强等[6]按产品交货期设置优先级,按优先级顺序完成多产品综合作业调度,该方法可高效求解小规模调度问题,但在大规模调度问题中难以取得最优解。

截止目前,智能算法在JSSP研究上已趋于成熟,但是关于CJSSP的研究尚有不足,由于CJSSP对产品工艺结构依赖过高,智能算法研究重点集中于编码设计方面。赵诗奎等[7]设计出了一种分区编码方式,虽能有效求解CJSSP问题,但减少了初始种群的多样性。石飞等[8]为避免分区编码方式遗漏解空间问题,采用了邻接矩阵修复方法,确保了初始解空间的完整性。王福吉等[9]设计了基于可行域搜索的遗传算法,在可行域内进行了交叉、变异操作,但缩小了搜索范围,不利于搜索全局最优解。智能算法在CJSSP问题应用上多采用遗传算法[10-12]。SEIDGAR H等[13]采用帝国竞争算法对装配作业车间进行了研究。蒋南云等[14]设计混合智能算法对可重入综合作业调度进行了研究,建立了双层作业计划。

上述学者虽对CJSSP问题有一定研究,但在多产品综合作业调度方面的研究仍有不足,难以实现对各个产品的高效调度;智能算法研究在编码设计上难以保证解空间的完整性,有时设计过于繁琐,对CJSSP问题的应用研究尚有欠缺。

针对上述存在的问题,本文以某重型装备为研究对象,针对不同交货期下的多产品综合作业调度问题,以加工成本、精准交付、跨车间转运次数为优化目标,建立多产品综合作业调度优化模型,设计改进量子遗传算法对模型求解;同时设计基于装配约束的编码方式,使染色体满足装配约束关系,最终确定各工序最佳执行时间,以提高重型装备生产调度的精益性指标。

1 重型装备生产调度问题分析

通常，重型装备是定制化生产的大型产品,由机械工厂(车间)按订单组织生产,由物料经非连续移动加工装配而成,生产设备以通用型为主,跨车间生产[15]。由于生产环境复杂多变,零件跨车间生产容易造成生产混乱,应尽量减少零件跨车间的转运次数。重型装备各部件关联性强,一般将产品分解为部件,根据订单交货期设定各部件排产优先级,按优先级从高到低进行排产,生成可行的作业计划。

精益生产强调“消除浪费,降低成本”的理念,上述排产方式只考虑交货期单一指标,且这种方式生成的作业计划很难确保订单精准交付。订单提前完工会产生库存,造成浪费;拖期完工又会给企业带来额外费用,影响客户满意度,难以实现生产调度精益性目标。

重型装备通常在多订单并行条件下组织生产,由于设备资源有限,产品对设备资源的不良占用会影响到其他产品的生产进度,导致订单不能按期交付,直接影响企业核心竞争力。多产品综合作业调度不同于单个产品综合作业调度,不能以产品完工时间最短为优化目标,需要合理安排各个产品每道工序的最佳执行时间,实现订单精准交付,对求解精度要求更高。重型装备生产调度要合理安排每个车间加工任务,使每个产品订单都能精准交付且成本最低。

2 多产品综合作业调度优化模型

2.1 模型假设

n个产品需要在多个车间加工装配,每个产品由o个工件组成,每个工件有q道工序,每道工序根据其工艺特点可在不同车间的设备上加工,工件的加工顺序严格按照工艺约束。

要求工件各工序对应合适的机床,确定最优调度方案,在生产中满足以下假设:

(1)工件的每道工序只能在一台设备上加工;

(2)在工件的紧前工件加工完成后才可开始加工;

(3)一台设备同时只能加工一道工序;

(4)加工过程中设备没有故障发生;

(5)零件的转运时间忽略不计。

2.2 相关符号定义

相关符号及定义如表1所示。

表1 符号定义

2.3 优化模型

综合考虑产品内部加工装配约束关系,笔者以加工成本、精准交付、跨车间转运次数为优化目标,建立多产品综合作业调度优化模型。

目标函数表示为:

f=λ1f1+λ2f2+λ3f3

(1)

式中:λi—目标函数加权系数;fi—第i个目标函数。

(1)加工成本。重型装备生产要考虑生产成本,以成本最低为目标,最小加工成本表示为:

(2)

(2)精准交付。产品订单应满足交货期要求,提前或拖期完工都会给企业带来损失。设置提前/拖期惩罚函数,若产品订单实际完工时间与交货期出现偏差会产生惩罚值,通过减小惩罚值实现产品精准交付,提前/拖期惩罚函数表示为:

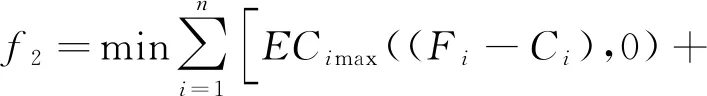
(3)

(3)跨车间转运次数。重型装备生产过程复杂多变,应尽量减少零件跨车间转运次数,避免造成生产混乱,最小跨车间转运次数表示为:

(4)

为使多产品综合作业调度优化模型有效求解,设置约束条件如下:

(5)

Sik1j≥Civ(v∈Bik)

(6)

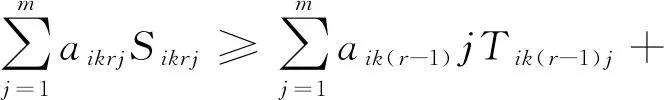
(7)

(Sikrj,Cikrj)∩(Sxyzj,Cxyzj)=φ

(8)

式(5)限制了工件i的每道工序,要求其只能在一台设备上加工;

式(6)限制了工件i第一道工序的开工时间,要求其不小于工件i紧前工件集的完工时间;

式(7)限制了工件的后道工序开始时间,要求其不早于前道工序的完工时间;

式(8)限制了每台设备,要求其同时只能加工一个工件。

3 改进量子遗传算法

量子遗传算法(QGA)在遗传算法(GA)的基础上融入量子计算,量子位编码方式增加了解空间的多样性。但是种群通过量子旋转门向最优个体逼近时,若没有更好的解出现,易陷入局部最优。模拟退火算法(SA)有很好的局部优化效果,以一定概率接受劣解。

改进量子遗传算法(SQGA)将SA与QGA结合,在种群迭代时易跳出局部最优,提高了算法全局搜索能力。同时,设计基于装配约束的编码方式和自适应旋转角,使其可以更平稳求解综合作业调度问题。

3.1 编码设计

CJSSP问题编码的关键是保证染色体在解码时满足装配约束,避免不可行解产生。本文设计基于装配约束的工序-设备-父节点3层编码方式,确保解码时染色体的可行性和解空间的完整性。

一条量子位编码染色体表示如下:

工序编码中,将十进制数值从小到大依次排列,将原位置索引值填入排列后的位置即得到工序编码。设工序i转化后对应的十进制数值为yi,可选设备的数量为wi,则工序i的设备编码为mod(yi,wi)+1。父节点编码为每道工序对应所属工件的紧后工件编号,根节点的父节点编码记为0。

设某产品由3个工件组成,每个工件1道工序,工序可选设备数均为2,在2台设备上加工。

产品结构如图1所示。

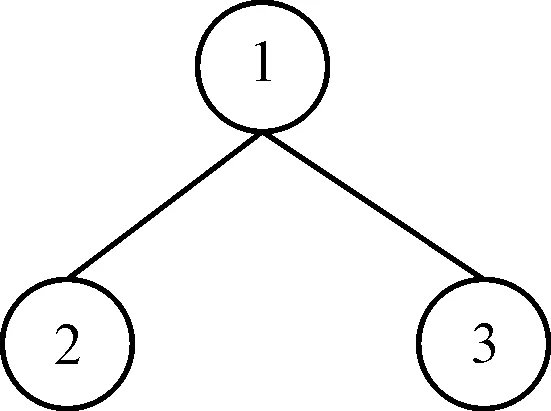
图1 产品结构

假设基于该产品设计的某条染色体在进行量子位测定时,量子位编码根据概率幅转换为二进制串101101,以此为例:

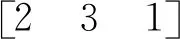
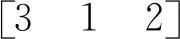
解码时,首先通过三层编码结构转换确保染色体的可行性,使其满足产品内部装配顺序约束。

具体操作如图2所示。

图2 三层编码转换操作

图2中,对工序编码从左至右进行遍历,若在第三层父节点编码中含有该工序对应编码信息则跳过,否则删除该工序编码对应索引位置的三层编码信息,并将删除的三层编码信息重新依次记录在新集合中。重复以上操作直至三层编码为空,即可得到符合装配约束的新染色体。

由于染色体转换前的编码是随机的,通过三层编码结构转换为满足装配约束染色体的解空间是完整的。根据新染色体序列从左至右进行解码,即可得到符合装配约束的各工序执行时间。

3.2 量子位更新策略

QGA中采用量子旋转门作用于染色体,通过改变量子位编码的概率幅更新染色体,实现种群进化,其更新如下:

(9)

式中:U—量子旋转门;θ—量子旋转角。

θ值影响种群收敛速度,太大会导致早熟,反之导致收敛过慢。θ取值一般为0.01π～0.05π,为使种群收敛速度更平缓,本文设计自适应调整θ为:

(10)

式中:fitnessn—个体n的适应度值;fmin—种群中最小适应度值,也是文中最佳个体适应度值;fmax—种群中最大适应度值;Δθ—0.05π。

与最佳个体适应度值越接近的个体,说明其性能优良,采用较小的θ值,降低收敛速度;反之,采用较大θ值。

3.3 模拟退火策略

量子位更新结束后,笔者取适应度值较好的前20%个体进行退火操作,以加快收敛速度;采用Pauli-X门互换αi和βi的概率幅,从而改变量子位测量值,完成邻域搜索。

设每个量子位进行Pauli-X门转换的概率为0.1,转换过程如下:

(11)

式中:X—Pauli-X门。

将邻域搜索后的最佳个体与之前最佳个体进行对比,按照Metropolis准则确定新个体接受概率,即:

(12)

式中:P—新个体接受概率;f(a)—邻域搜索前最佳个体适应度值;f(b)—邻域搜索后最佳个体适应度值;T—退火温度,T=D×T0;D—温度衰减参数;T0—初始温度。

3.4 适应度函数

模型求解过程中,依据适应度函数去评定个体的好坏,适应度函数一般由目标函数进行尺度变换演变生成。由于目标函数式(1)是由3个目标加权组合而成,单位不统一,在加权组合前要进行标准化处理,化为无量纲形式,适应度函数式为:

(13)

(14)

3.5 算法流程

改进量子遗传算法(SQGA)将量子遗传算法(QGA)与模拟退火算法(SA)结合,具体算法流程如下:

Step1初始化量子位编码,产生随机初始种群Q0;

Step2将Q0进行测定、转化,得到种群S0;

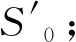
Step4进行适应度计算,保留最佳个体Pb;

Step5量子门旋转,得到新的种群S;

Step6将S经染色体转换,进行适应度计算,保留新的最佳个体Pb;

Step8判断是否满足终止条件,如果满足转向Step9,否则种群迭代次数加1,转向Step5;

Step9算法搜索结束,输出最优解。

改进量子遗传算法的算法流程图如图3所示。

图3 算法流程图

4 实验仿真与分析

笔者采用MATLAB R2014a进行实验。算法参数设置如下:种群规模100,迭代次数200,GA交叉概率Pc=0.85,变异概率Pm=0.2,QGA固定旋转角,SQGA温度衰减参数D=0.95,初始温度T0=100,终止温度Tmin=1。

实例验证首先对标准算例仿真,验证SQGA算法性能,再将算法应用到重型机械企业的生产实例中。

4.1 算例测试

目前,对CJSSP基准测试问题研究较少,为验证改进量子遗传算法的有效性,笔者采用文献[11]中的10个算例测试,以makespan为优化目标,使产品完工时间最短。

产品结构如图4所示。

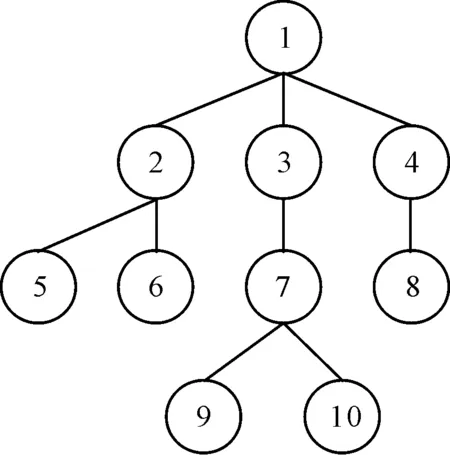
图4 算例产品结构

笔者采用GA、QGA、AQGA、SQGA算法进行实验且都采用本文设计的基于装配约束的编码方式,其中,AQGA在QGA的基础上加入自适应旋转角,算法其余部分相同。

每个算例仿真实验次数为10次,以最优解(Optimal)、最优解占比(Ratio)、平均收敛代数(Gen)为衡量指标。

具体数据如表2所示。

由表2可知:

表2 不同算法数据对比

(1)Optimal指标上,SQGA效果最好,求解精度最高,10个算例均能取得最优解;QGA和AQGA寻优效果接近,仅在Orb3C算例没能收敛至最优;GA寻优效果最差,但大部分算例也能收敛至最优。可知本文设计基于装配约束的编码方式在CJSSP问题上具有非常好的效果;

(2)Ratio指标上,SQGA在Orb3C、Orb4C、Orb6C 3个算例上分别为0.8、0.9、0.8,其余算例为1,均优于GA、QGA、AQGA,说明SQGA求解过程平稳,该算法有较好的稳定性;

(3)Gen指标上,SQGA仅在Orb3C算例没取得最小值,但寻优效果均优于其余3种算法。整体上,SQGA算法收敛速度最快。此外,AQGA仅在Orb2C和Orb3C两个算例上的平均收敛代数大于QGA;在Orb3C算例上,AQGA寻优效果优于QGA,说明QGA采用自适应旋转角可以提高收敛速度。

综合以上3项指标,可见4种算法中性能最好的为SQGA,其次为AQGA、QGA、GA;综合10个算例,SQGA相比QGA,平均收敛代数减少18.6%,平均最优解占例增加26%,SGQA具有更好的收敛效果和求解精度。

笔者以Ft10C为例进行说明,其最优结果甘特图如图5所示。

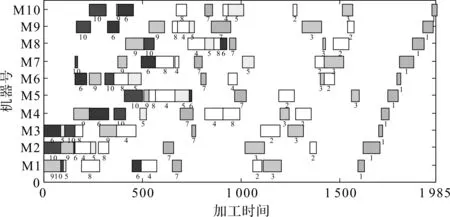
图5 Ft10C甘特图数字—工件号;横坐标—加工时间;纵坐标—机器号

由图5可知:4种算法均能取得Ft10C,其中算例最优完工时间1 985。

算法最优收敛曲线如图6所示。

图6 Ft10C不同算法收敛曲线

由图6可知:SQGA算法在11代收敛至最优,GA、QGA、AQGA分别在25、20、16代收敛至最优;由此可见,SQGA收敛效果最好,验证了改进机理的合理性和有效性。

4.2 实例验证

4.2.1 实例数据

现有Φ7×3.5 m半自磨机1台,Φ5.5×1.8 m半自磨机2台,以二班制方式生产,每班8 h,交货期分别为25 d和35 d。

半自磨机产品结构如图7所示。

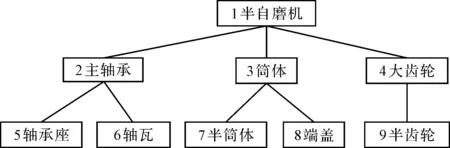
图7 半自磨产品结构

半自磨机由主轴承、筒体、大齿轮3大零部件构成,产品拖期一天扣除合同金额千分之一,拖期惩罚系数FC1取450,FC2、FC3取350;产品提前完工会占用库存、设备资源。经综合考虑,笔者设置提前惩罚系数ECi为200。

实例中设备信息如表3所示。

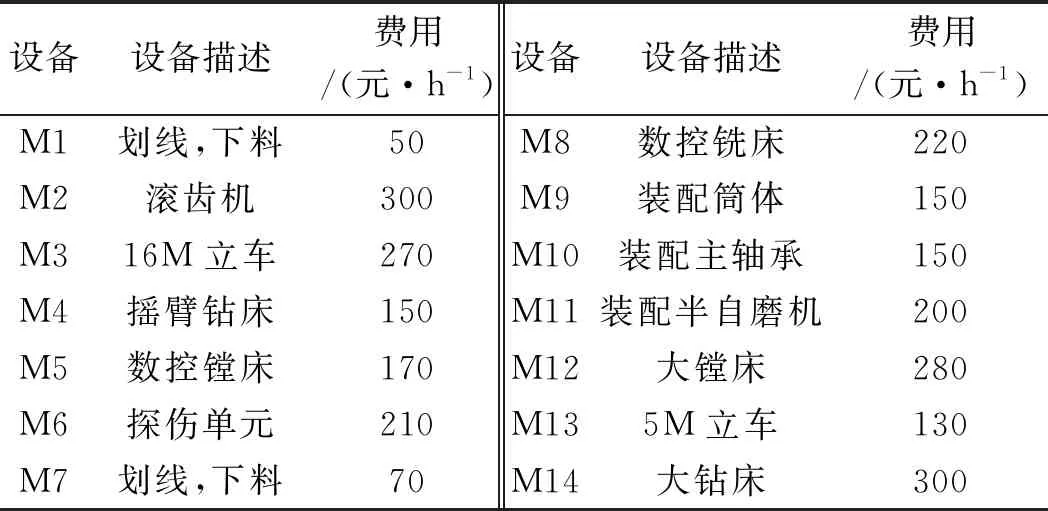
表3 设备信息

由表3可知:M1～M6属于数一车间,M7～M11属于数二车间,M12～M14属于粗加车间,半自磨机在数一、数二、粗加3个车间进行生产。

工序可选择机床和加工时间如表4所示。

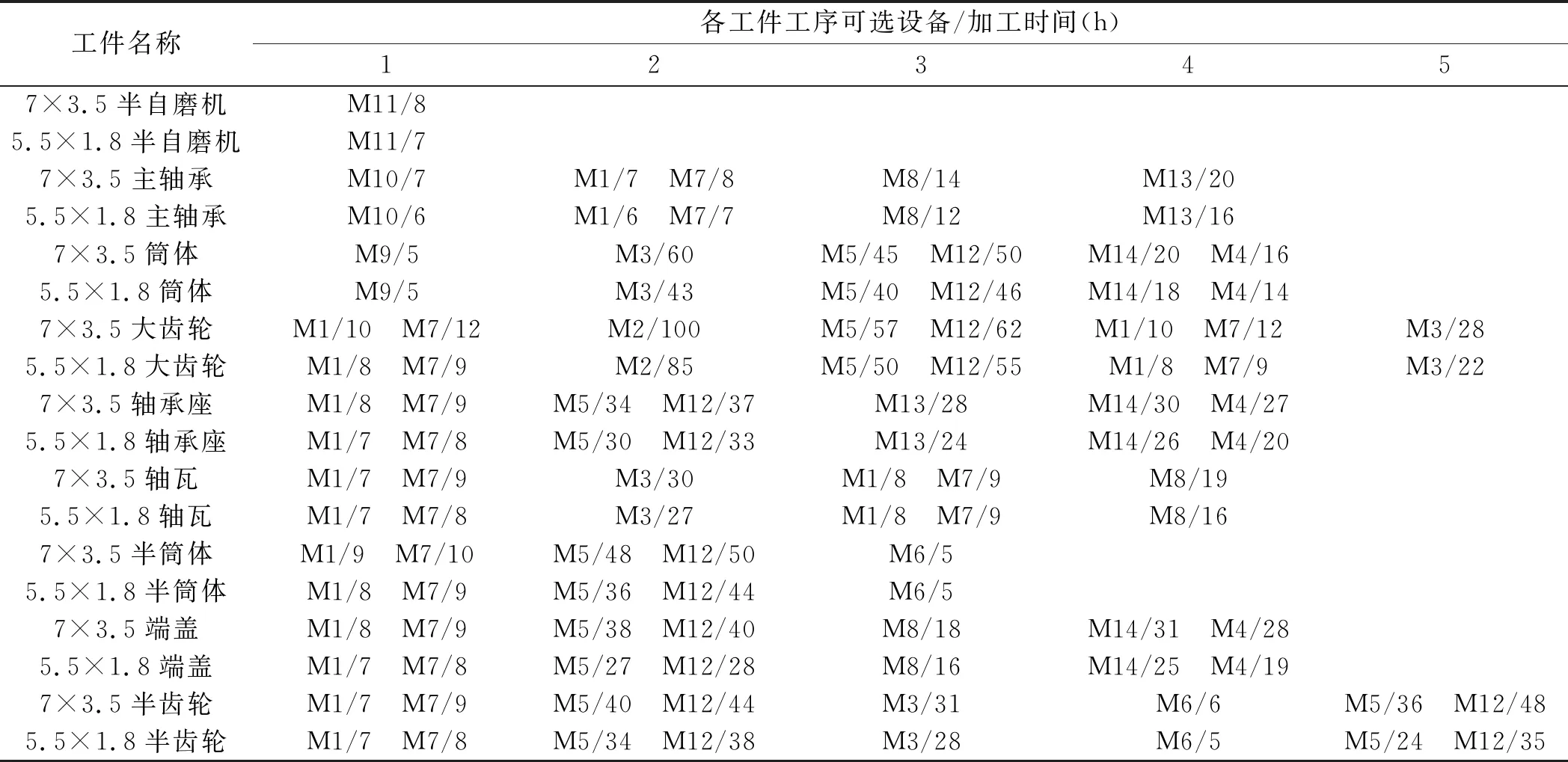
表4 工序信息

4.2.2 实例仿真

实例仿真以式(13)为适应度函数,根据目标重要程度设置权重λ1=0.4,λ2=0.4,λ3=0.2,以保证相应指标达到最优,采用SQGA算法对多产品综合调度模型进行求解。

半自磨机排产调度甘特图如图8所示。

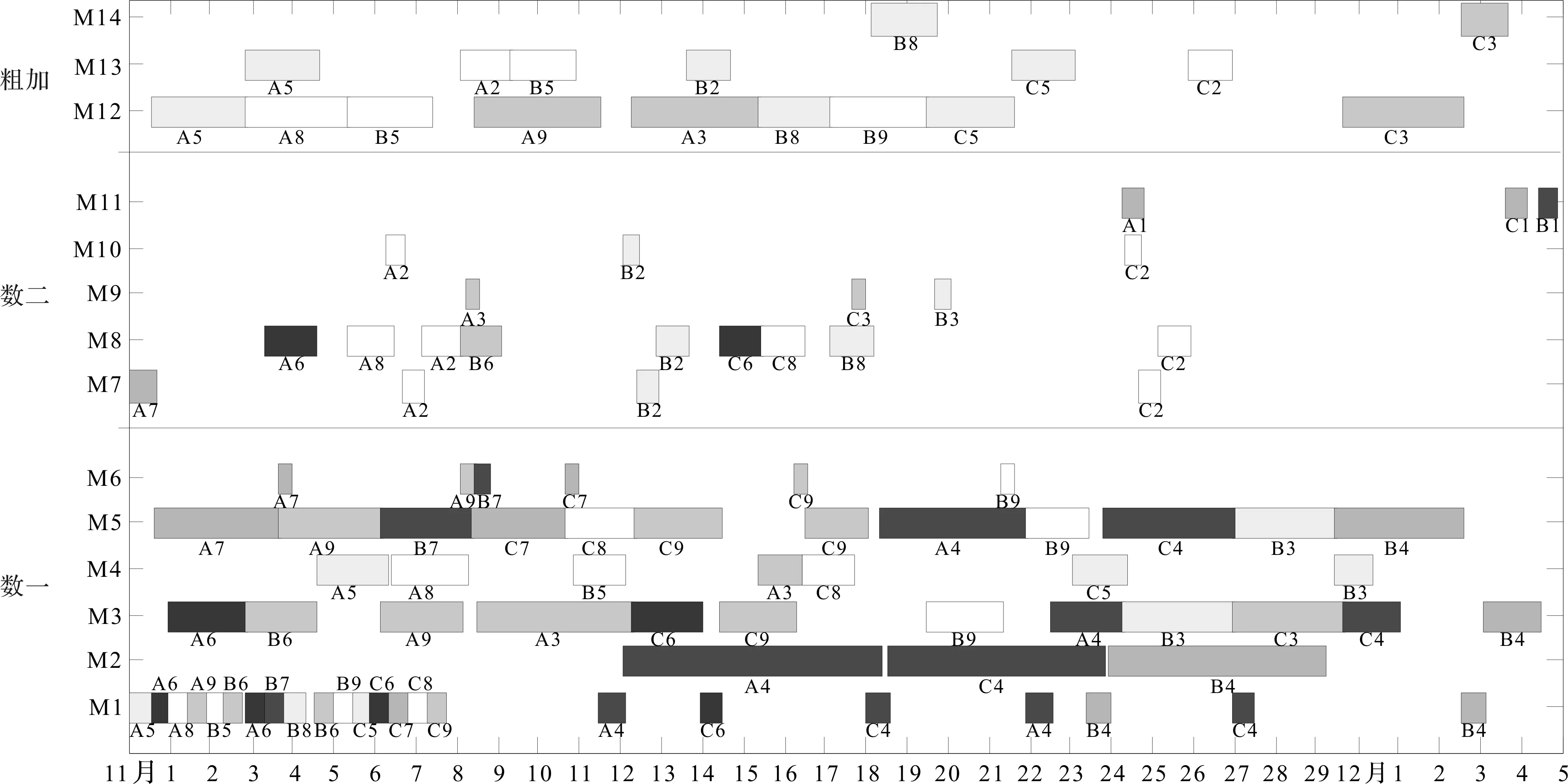
图8 半自磨机排产调度甘特图

图8中,A代表7 m×3.5 m半自磨机,B和C代表5.5 m×1.8 m半自磨机,字母后的数字代表工件,如:A2表示7 m×3.5 m半自磨机的第2个部件主轴承。

SQGA算法的收敛曲线如图9所示。

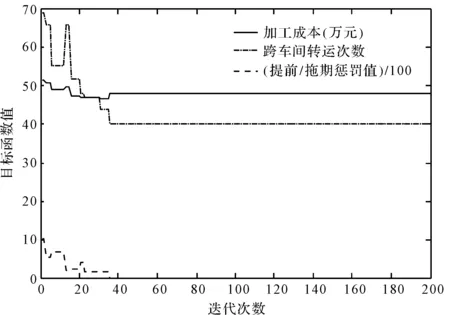
图9 SQGA收敛曲线

4.2.3 效果分析

目前,该企业采用APS制定作业计划,将产品分解为部件,每个部件根据交货期紧迫度设定排产优先级,按照排产优先级进行排产。即当某个部件排产完成后,才开始为优先级低的部件排产,这样使得解空间缩小,很难排出较好的调度结果。采用综合调度对产品进行排产,可以将产品分阶段调度变为产品链调度,有效缩短产品生产周期。

笔者将SQGA+综合作业调度与企业采用的APS+部件优先级调度进行对比,结果如表5所示。

表5 数据对比

由表5可见:SQGA+综合调度方法使加工成本减少了7.8%,跨车间转运次数减少了30.4%,产品达到精准交付,提高了机械工厂(车间)的生产调度精益性指标。

5 结束语

针对重型装备加工与装配集成调度精益性不足的问题,综合考虑加工成本、精准交付、跨车间转运次数等目标,笔者建立了多产品综合作业调度优化模型;为使模型得到有效求解,笔者设计了改进量子遗传算法;针对量子遗传算法易陷入局部最优的缺点,将其与模拟退火算法相结合,提高了算法的搜索精度;在编码方式上设计了一种基于装配约束的工序-设备-父节点三层编码结构,使染色体在解码时,既能够满足装配约束关系,又能够满足解空间的完整性;最后,通过算例和生产实例对算法和模型的效果进行了验证。

研究结果表明:与传统量子遗传算法相比,改进量子遗传算法具有更好的寻优效果,收敛速度和求解精度更优,可高效求解综合作业调度问题。此外,该模型和算法可以提高重型装备精益化生产调度指标,为重型装备精益化生产提供理论依据。

在接下来的研究中,笔者将以鲁棒性为目标,对多产品综合作业调度进行研究,以应对重型装备生产过程中的突发情况对调度计划带来的不良影响。