薄膜型局域共振隔声罩隔声特性

吕东方， 靳国永， 叶天贵， 胡世尧

(哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001)

船舶及其动力设备产生的低频噪声由于穿透力强、衰减缓慢、传播距离远等特点引起了越来越多的关注，由于传统隔声材料受到质量定律的限制，传统的轻质隔声材料很难有效地隔绝低频噪声[1]。近年来，声学超材料的出现为低频隔声设计提供了新思路，特别是薄膜型局域共振声学超结构，具有重量轻、体积小、针对性强等优点，在船舶与海洋工程的低频隔声领域具有广阔的应用前景[2]。近年来，学者们在开发新型的、轻质的局域共振声学结构方面做了大量的研究工作，这些结构可以在低频范围内达到出色的降噪效果。其中，薄膜型声学超材料(AMs)的研究引起了研究者的广泛关注。Yang等[3]提出了用于低频噪声绝缘的膜型声学超材料，该团队通过在带有夹紧边界的膜上附加一个小质量，并在前2个共振频率之间调谐一个窄带负动态有效质量，通过这种方式打破了质量定律的限制。薄膜型局域共振结构已经衍生了许多新兴的结构形式和新型材料。Narify等[4]为了改善传统薄膜型声学超材料隔声峰单一且频带过窄的情况，通过有限元仿真和实验测量等方式，研究发现不同形式的附加质量结构不仅可以增加隔声峰的高度，还可以有效将隔声带变宽。Lu[5]制作了不同偏心质量的声学超材料，通过不同组合模型的仿真模拟，确立了不同结构单元的反共振峰优于单个单胞的低频有效区间。Zhao等[6-7]构建了一种膜上添加钢质量块和磁铁的声学超材料，利用磁力动态效应可调控薄膜刚度，从而进一步改变隔声幅值的位置，且通过实验证明了该仿真结果的正确性。Ning等[8]通过将薄膜设计为带孔的弹性质量块形式，把薄膜型声学超材料变成可调谐，通过施加不同方向的挤压力来实现薄膜变形，结果表明，变形后的低频局部共振带隙在0.197～0.226处的位移移动并加宽到0.168～0.364，带隙增加了7.76倍，为低频降噪提供了新的思路。但是，目前对于大尺寸薄膜型局域共振声学结构隔声特性的研究很少。因此，有必要针对船舶舱室及动力设备的低频噪声问题，围绕薄膜型局域共振声学结构对其隔声机理、不同结构参数对其隔声性能的影响规律、隔声频率和频段的调节机制展开研究。以方便对大尺寸局域共振声学结构进行设计，为满足实际工程需要的大型隔声构件提供方便有效的指导。

1 薄膜结构隔声性能计算理论基础

计算中采取平面波作为入射声场，通过声波的传播方程来推导匀质板结构和薄膜型局域共振声学结构的传递损失计算方法。一维声波波动方程为[9]：

(1)

此偏微分方程的解的形式为：

p(x,t)=f(ct-x)+g(ct+x)=

f(wt-kx)+g(wt+kx)

式中：波数k可以定义成声波频率w和声速c的比值；声压p和介质质点振速v为：

p(x,t)=aej(wt-kx)+bej(wt+kx)

(2)

(3)

当b=0时，可以看作声波没有反射效果。假设将声源在开始的声压定义成pa，那么可以求得平面声场中的声压为：

p(x,t)=paej(wt-kx)

(4)

相应的，质点振速方程为：

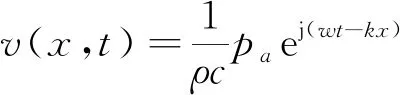
(5)

图1为平面波在不同介质中传播和转换的简化模型，模型包括两边的完美匹配层(PML)和空气腔以及图中灰色区域OD处的声学超材料结构。

图1 平面波在不同介质中传播和转换示意

两边空气和OD处的声阻抗分别假设为ρ1c1和ρ2c2，简化模型的平面波方程可以写为：

(6)

式中：k1和k2分别表示空气中和声学超材料中的波数，由声波频率与空气和声学超材料中的声速比值求得。将模型灰色区域处的D点看作原点，透射部分波的传播方程可以表示为：

(7)

由图1可以看出，在空气与声学超材料的交界处可以建立起声压与质点振速的连续边界条件：

(8)

一维声场的平面波传播时，可以得到：

(9)

根据前面的透射波声压方程和入射波声压方程，声强可以表示为I=P2S/ρc(S表示声波作用面积)，相应的透射系数tI可以写成透射声强It与入射声强Ii的比值：

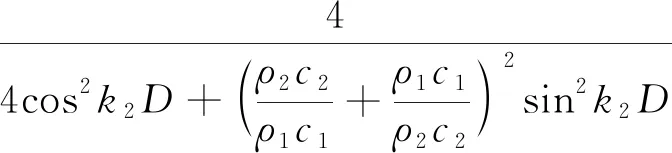
(10)

所以薄膜型局域共振声学结构的传递损失为：

(11)

2 薄膜型局域共振隔声罩隔声特性研究

2.1 声学结构单元设计

为了分析结构的低频隔声特性，本文取一个单胞结构进行具体分析，结构模型如图2所示。薄膜选用边长20 mm、厚度为0.2 mm的硅胶；刚性框架采用铝作为计算材料，高度10 mm，厚度1 mm；初始预应力1 MPa。材料参数见表1。对于单胞来说，铝质框架的第1阶振动模态远大于薄膜的第1阶振动模态，对隔声量影响忽略不计，可以看做固支边界。

表1 单胞模型材料参数表

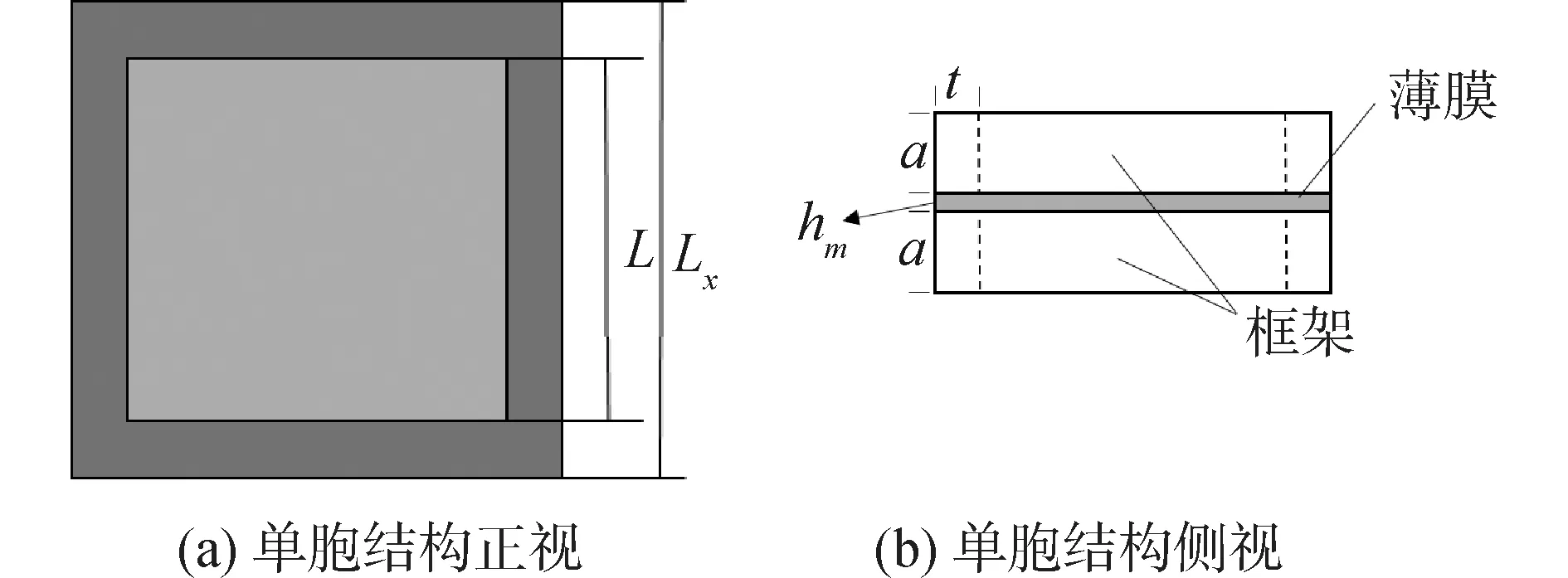
图2 声学超材料单胞示意

结构隔声量的求解主要通过多物理场数值分析软件中的压力声学物理场和结构力学物理场来实现。入射压力场类型采用平面波，压力幅值为1 Pa，垂直声学结构单元入射，吸收边界选用辐射边界来模拟无反射边界。声场四周选用硬声场边界，声学结构边界选用固定边界。隔声量求解的有限元模型如图3所示。

图3 有限元数值模拟模型示意

声场频域分析范围为10～1 500 Hz隔声量的计算结果如图4所示。

图4 声学超材料和同质量的均质材料隔声曲线

由图4可知，薄膜型声学超材料的第1阶共振频率为1 164 Hz。作为对比，图4中还给出了相同质量密度不同边界条件下的均匀介质板结构的隔声量，在刚度控制区范围内薄膜型声学超材料的隔声性能要远优于同质量密度的均质材料。体现出了薄膜型局域共振声学结构在处理低频隔声问题上的优势。

2.2 低频声机理分析

通常无限周期性排列的固支边界薄膜系统在声压的激励下振动，整个系统在第1阶固有频率下的等效质量密度为负，利用有限元手段可以计算其等效质量，即薄膜表面受到的平均声压和薄膜平均法向加速度的比值：

(12)

图5为薄膜系统隔声机理计算结果，图5中给出了薄膜等效质量与薄膜平均法向位移的数值模拟结果。随着频率的增加，薄膜的等效质量密度从负值逐渐趋近于零，当频率达到1 164 Hz时，薄膜等效质量密度为零，在1 164 Hz以后，薄膜等效质量密度变化为一个大于零的常值。在薄膜等效质量密度由负值转为正值处，薄膜的平均法向位移也发生了相变。薄膜平均法向位移的翻转意味着穿过声学结构单元的声压方向发生了改变，在声与结构耦合的作用下，薄膜的振动可以直接影响透射声压，所以薄膜结构的隔声性能与振动模态息息相关。

图5 薄膜等效质量密度和薄膜平均法向位移计算结果

2.3 附加质量作用分析

2.3.1 附加质量重量对隔声量的影响

保持薄膜参数不变，在薄膜中心添加一个半径为r=3 mm，h=1 mm的圆柱形钢块，结构模型如图6所示。

图6 薄膜质量块型声学超材料结构示意

图7分别给出了质量块重量为0.1、0.2和0.4 g下的隔声曲线:

图7 不同附加质量重量下的隔声曲线

在薄膜上添加质量块后，结构会出现不同高度的隔声峰，当薄膜附加质量为0.1 g时，隔声峰幅值为66 dB，第1阶共振频率位置为420 Hz，随着附加质量的增加，薄膜隔声峰逐渐向低频移动，隔声峰幅值逐渐增大，当附加质量为0.8 g时，隔声峰幅值增加至69 dB，隔声谷位置提前到223 Hz。所以，通过调节质量块的重量可以增加100 Hz以上的频段的隔声峰数量，但是质量块的重量的增加会导致隔声谷的位置提前，对于100 Hz以内的低频噪声并不能有效隔离。

2.3.2 附加质量尺寸对隔声量的影响

保持质量块的质量和位置不变，改变质量块的尺寸也会对结构的隔声量造成影响。图8展示了0.2 g不同尺寸附加质量块的隔声曲线。随着频率的升高，不同尺寸质量块的隔声曲线变化趋势相同，增大附加质量块尺寸的同时，薄膜的隔声低谷和隔声峰会向高频移动，隔声峰幅值逐渐升高；隔声低谷的频率从244 Hz增加到400 Hz，相对应的隔声峰幅值从48 dB升高到60 dB；在0～200 Hz内有效隔声带宽逐渐增加，低频隔声性能逐渐提升。

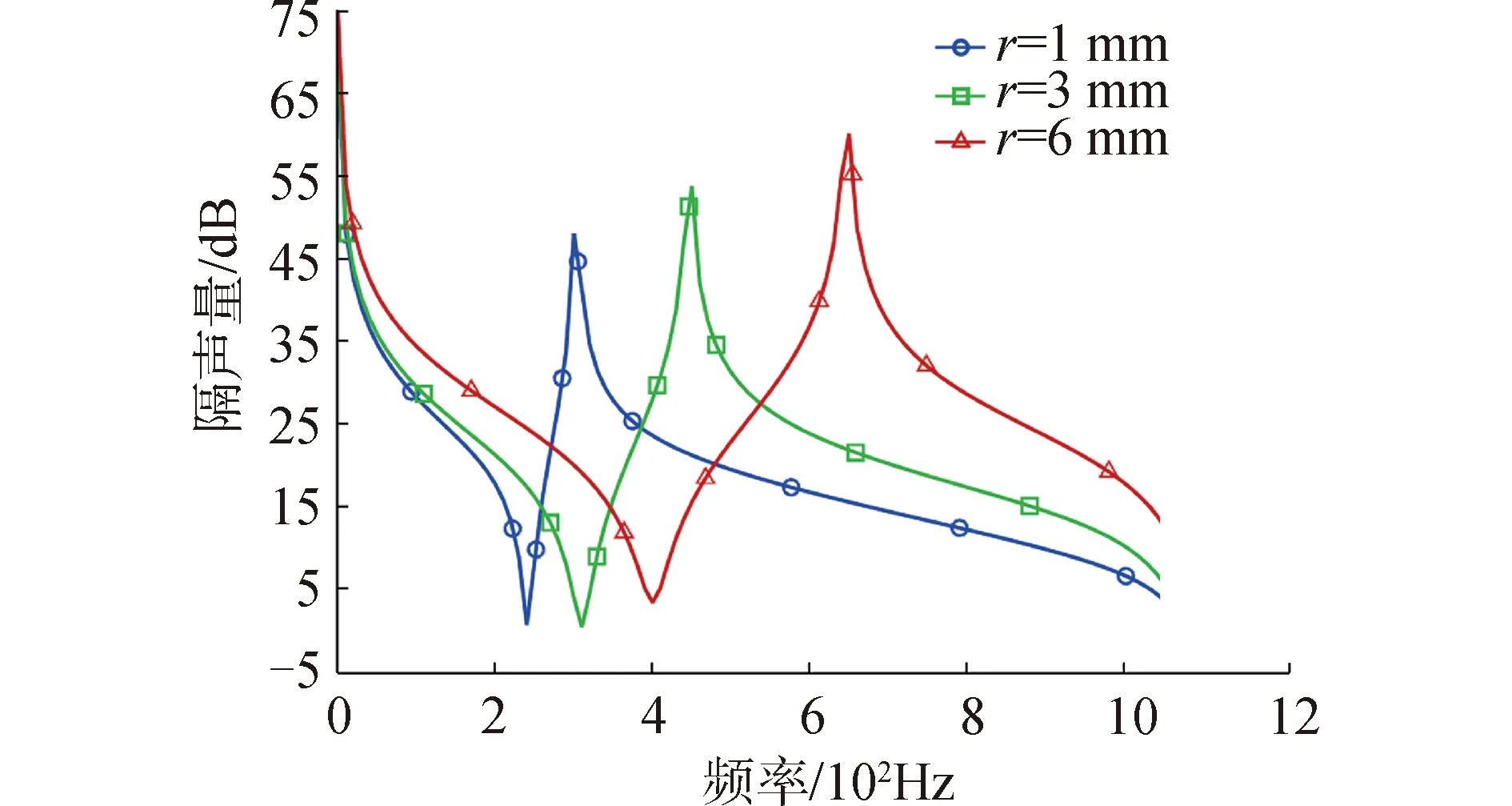
图8 不同附加质量尺寸下的隔声曲线

2.4 计算验证与实验对比

在薄膜型声学超材料的发展过程中，大量的学者通过理论和实验对不同形式的声学超材料进行了验证以及优化设计，由于本文主要针对大尺寸构件的隔声特性进行分析，为了验证本文仿真方法的正确性，选取了Sui[10]的实验结果进行仿真方法验证。该蜂窝超材料的蜂窝结构由芳纶纤维制作，t=0.07 mm，l=3.65 mm，hc=25 mm。薄膜采用乳胶橡胶，厚度hm=0.25 mm。芳纶纤维板和乳胶橡胶的材料参数如表2所示。

表2 芳纶纤维板和乳胶橡胶材料参数

文献[10]蜂窝声学超材料有限元模型如图9所示。

图9 文献[10]实验试件以及本文所建仿真模型

由图10可知，本文所计算的有限元解与文献有限元解基本一致，在500 Hz以内的低频段隔声量特别高，隔声量随着频率的增加逐渐降低，在1 100 Hz左右出现第1个隔声谷，隔声谷频率相差8～10 Hz。因为本文在有限元计算时未添加材料阻尼，所以隔声谷幅值与实验值略有差异；由于试验样件的加工差异以及阻尼因素的影响，本文通过计算薄膜材料阻尼比0.2下的隔声量与文献实验值进行对比，发现隔声曲线变得更加平滑，与文献实验值更加贴近，通过有限元解与实验值的对比，可以验证本文方法的正确性和准确性。

图10 本文有限元解与文献有限元和实验TL数据对比

2.5 大尺寸薄膜型局域共振结构隔声特性分析

2.5.1 单层薄膜型声学结构的建立

声学结构小试件是由5个周期性排列的边长为20 mm的单胞组成，小试件整体尺寸为110 mm；框架选用厚度为2 mm的铝；初始预应力为1 MPa；采用固支边界；材料参数与单胞模型一致。小试件模型与单胞模型的隔声曲线如图11所示。

图11 单胞模型与小试件模型的隔声曲线对比

小试件模型不仅要考虑相同单胞之间的作用，还需要考虑框架对整体结构隔声量的影响。从图11可知，相比单胞模型，小试件在1 012 Hz和1 250 Hz处出现了2个隔声峰。为了便于深入分析框架对结构隔声量的影响，各个隔声谷和隔声峰处的振型如图12所示。

试件由25个相同的薄膜单元组成，由图12可以看出，962 Hz处隔声谷框架和薄膜的振型主要集中在试件中心处，两者振动方向一致，由此可以推断出隔声谷是由于框架和薄膜单元共振引起的；1 082 Hz处隔声谷四周的薄膜单元振动位移较大，框架的振型主要集中在构件中心处，这是由同向的薄膜单元与框架共振引起。在1 012 Hz处，四周薄膜单元与框架振动方向反向，中心处少部分薄膜单元与框架振动方向同向，由此可以得出1 012 Hz处隔声峰是由框架以及四周反向振动的薄膜单元形成；同理，第2个隔声峰由构件中心反向振动的薄膜单元和构件形成。

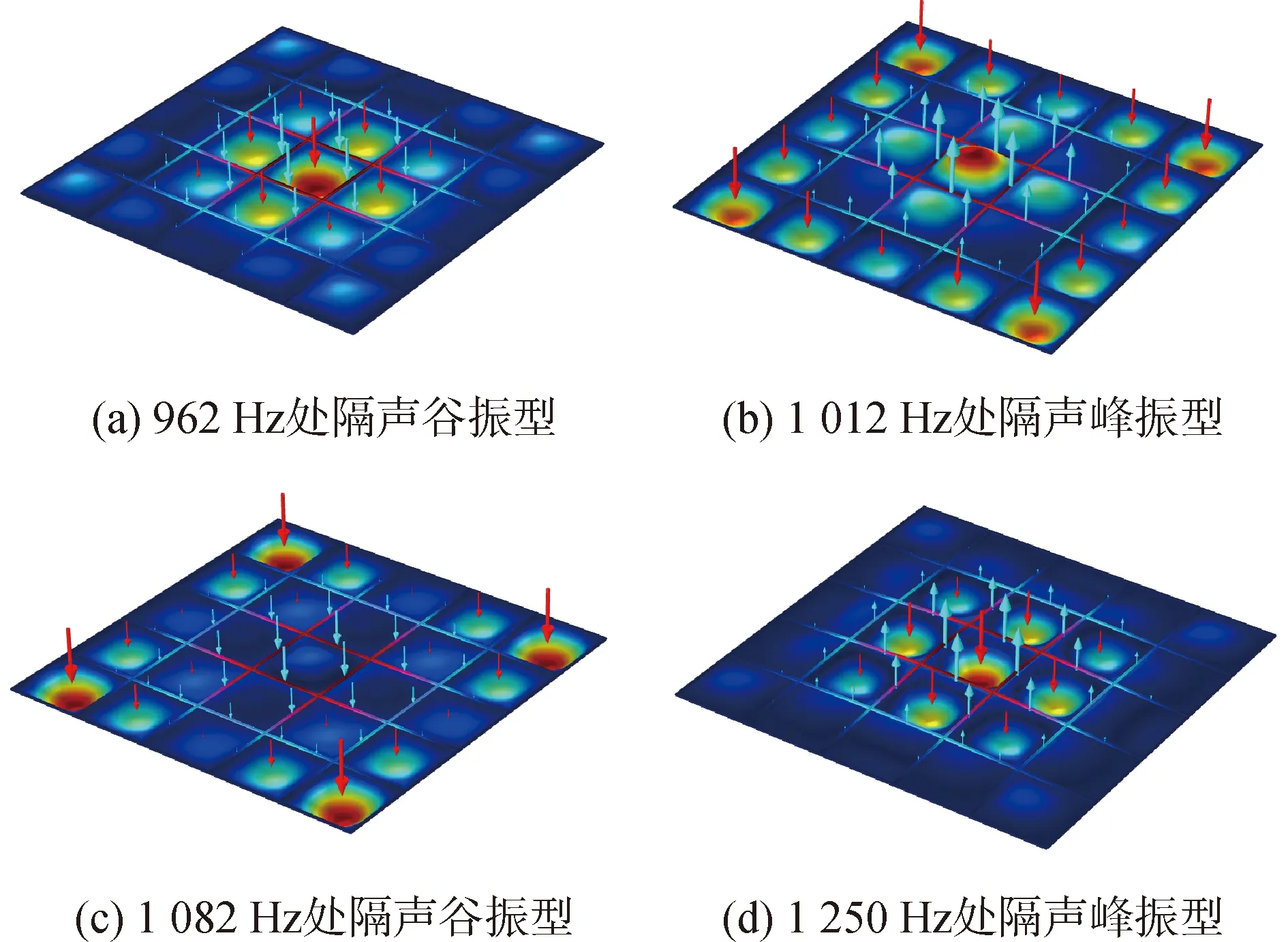
图12 小试件模型各个隔声谷和隔声峰处的振型

2.5.2 双层薄膜质量块型声学结构隔声特性分析

由于薄膜型声学结构整体厚度非常小，结构轻质，所以本节将在厚度方向只有4～6 mm的单层薄膜型声学结构的基础上研究双层声学超材料的隔声性能。其结构模型如图13所示。

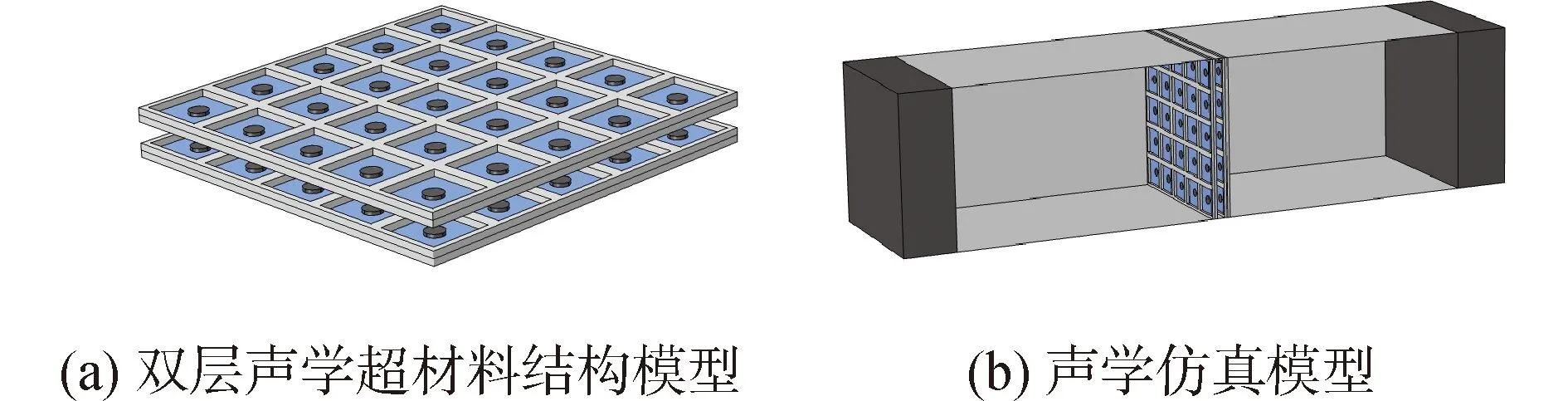
图13 双层薄膜质量块型声学结构模型示意

图13所示的双层声学超材料结构,材料参数与单层声学超材料结构相同，几何模型与单层声学超材料一致，薄膜质量块型声学结构双层膜之间的空腔为10 mm，双层薄膜质量块型声学超材料初始预应力改变为0.3 MPa，质量块半径为3 mm，附加质量为1 g。

由图14可知，随着频率升高，高预应力的单层薄膜型声学结构的整体隔声量要比双层薄膜质量块型声学结构高10 dB，600 Hz以后双层薄膜质量块型声学结构的隔声性能大幅提高，隔声峰出现在647 Hz处，最大隔声量为67 dB。虽然双层薄膜质量块型声学结构在600 Hz以后隔声性能很好，但是对于低频段的隔声量整体低于单层薄膜型声学结构，所以要对双层薄膜型声学结构进行改进。

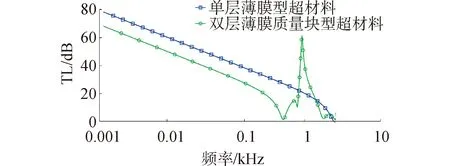
图14 单层薄膜型声学结构和双层薄膜质量块型声学结构的隔声曲线

2.6 大尺寸局域共振复合声学结构优化设计

2.6.1 不同预应力下大尺寸构件隔声特性分析

前面对100 mm小试件进行了隔声特性分析。本节将针对具体隔声罩构件面元进行优化设计。首先建立边长为1 m的正四边形试件，胞元尺寸为10 mm；薄膜厚度为0.2 mm；框架为长6 mm宽为6 mm的矩形框架。初始预应力作为影响薄膜型声学结构隔声性能的重要参数，首先计算不同预应力下1～5 000 Hz频段内单层薄膜型局域共振声学结构的隔声曲线。预应力在1 MPa和3 MPa下的隔声曲线如图15所示。

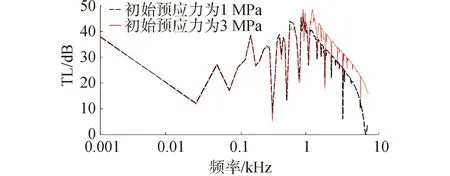
图15 不同预应力下的单层薄膜型局域共振声学结构隔声曲线

由图15可以看出，由于构件整体尺寸的变大以及胞元面积的减小，框架与各胞元之间的相互振动变得复杂且剧烈，框架与胞元和胞元与胞元之间相互影响，大尺寸隔声构件的隔声曲线相对声学超材料单胞模型以及小试件模型的隔声曲线有较大的不同。首先，2种结构的隔声曲线在41 Hz处出现第1个隔声峰，峰值为26 dB；在120 Hz出现第2个峰值为38 dB的隔声峰，200 Hz以后的隔声幅值均在35 dB以上，600 Hz以后预应力为3 MPa的隔声构件的隔声性逐渐优于预应力1 MPa的隔声构件，隔声量平均提高7～9 dB。总的来说，2种结构的隔声量在低频段相差不大，低频段预应力1 MPa的构件隔声性能略微优于3 MPa的构件，中高频段预应力3 MPa构件的隔声性能比预应力1 MPa的构件好得多。

2.6.2 大尺寸隔声构件框架优化设计

为了减小框架材料对结构隔声性能的影响，并且同时实现减重效果，将大尺寸隔声构建的框架设计为由正四边形框周期性延展而成的结构。计算所需材料参数详见表3。

表3 框架以及吸声材料参数

不同形式的薄膜型局域共振声学结构框架隔声曲线如图16所示。

图16 框架优化后的单层局域共振声学结构隔声曲线

在整个计算频段范围内，铝框架的隔声量要高于有机玻璃框架构件，但有机玻璃具有密度小、重量轻、刚度小等优点。2种框架的宽度方向过大都会产生透声现象，且随着频率的升高，优化型声学超材料构件隔声曲线斜率增大，并且在60 Hz处隔声谷的位置转变为隔声峰，隔声量为34 dB；在600 Hz以后的中高频段隔声性能良好。总的来说，框架长度方向和厚度方向优化后某些特定频段隔声性能得到了提高，但是整体隔声性能低于铝质框架，在实际工程中可以根据重量、加工难度以及构件强度等要求选用合适的框架。

2.6.3 大尺寸局域共振复合结构隔声特性分析

岩棉作为吸声材料贴敷或填充在隔声构件中可以获得更好的隔声效果。本节将对3层膜结构添加2层岩棉板的大尺寸局域共振声学结构进行隔声特性分析，结构初始预应力为3 MPa，岩棉厚度为20 mm、结构因子为1.2。图17模拟了四周固定边界下，阻尼比取0和0.2时大尺寸薄膜型局域共振复合结构隔声特性。

由图17可以看出，经参数优化后设计的薄膜型局域共振复合结构在中高频段具有优异的隔声性能，最大隔声量可达90 dB。在低频段，结构的第1个隔声谷出现在100 Hz处，隔声量为12 dB；250 Hz处有一个36 dB的隔声峰；452 Hz以后隔声峰幅值均在80 dB以上，隔声效果非常好；2 000 Hz以后，隔声曲线呈下降趋势。厚度为20 mm的岩棉在中高频起到了非常大的作用，部分频段吸声系数在0.9以上。当薄膜的阻尼比设置为0.2时，2 000 Hz以内的隔声量没有变化，随着频率的增大，2 000 Hz以后结构隔声量相比无阻尼的结构有很大的提升，说明附加吸声材料可以改善中高频段的隔声性能。

图17 不同阻尼比下薄膜型局域共振复合结构隔声曲线

2.7 薄膜型局域共振隔声罩设计及隔声性能分析

2.7.1 仿真模型的建立

根据船舶空气压缩机的设备参数与规格，局域共振隔声罩尺寸设置为1.5 m×1 m×1 m，罩面由边长25 mm的正四边形胞元组成，框架采用长8 mm宽4 mm的铝，薄膜采用硅胶作为材料，材料参数详见表1。隔声罩将采用壳梁耦合的方式进行建模计算，模型由半径为2.8 m的1/4圆作为声场区域，通过在模型对称边界处施加对称边界条件来模拟完整局域共振隔声罩模型。其中空气声场区域外层位置设置200 mm的完美匹配边界层(perfectly method layer，PML)用来模拟无反射吸收边界。在隔声罩对称面中间位置处放置一个单极子无指向性声源来模拟噪声源。仿真模型如图18所示。

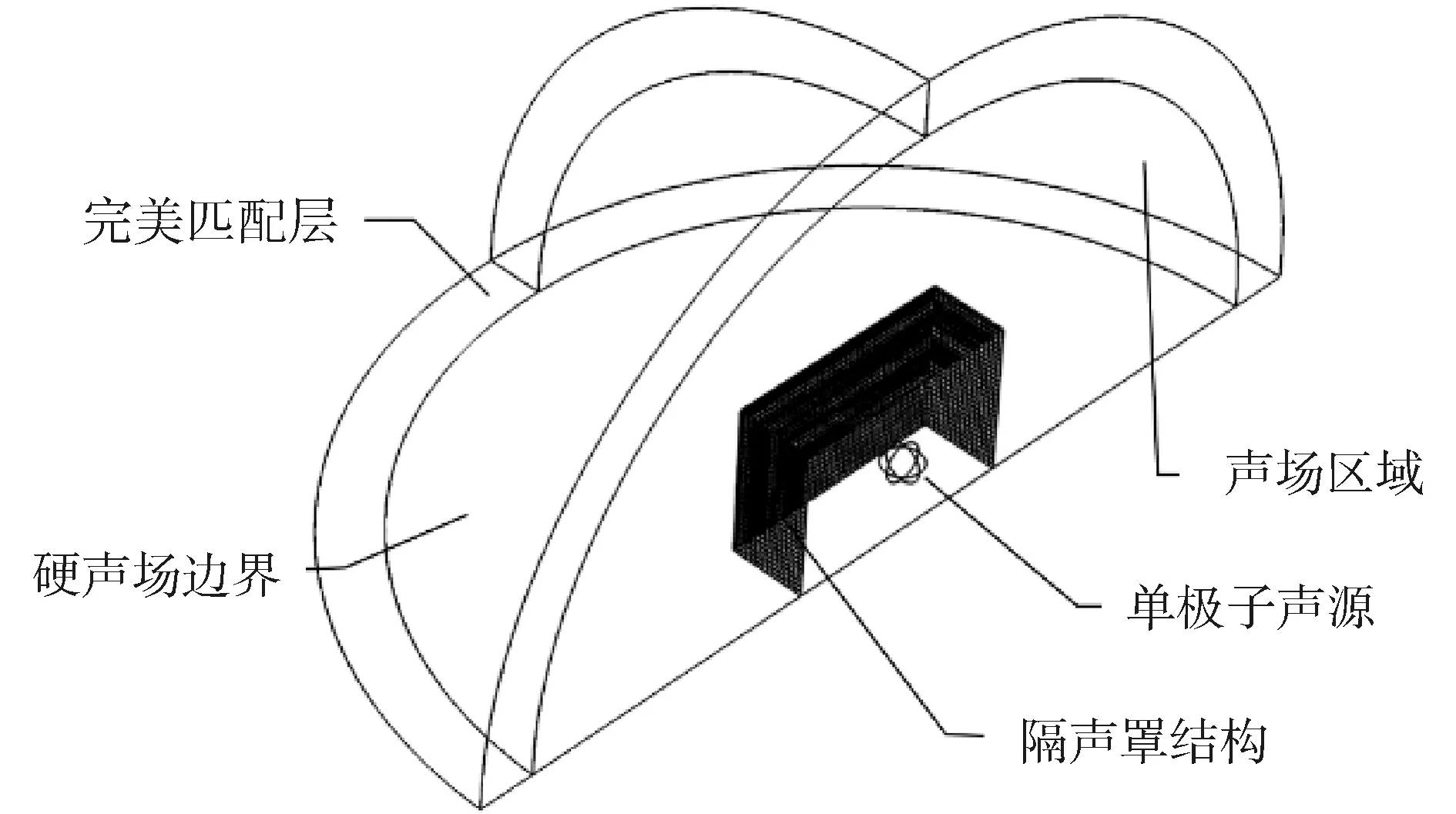
图18 局域共振隔声罩仿真模型示意

根据《船舶及产品噪声控制与检测指南》中的测试及操作，测点位置需距离动力设备隔声罩表面1 m。本文利用带有完美匹配边界层的球形声场区域来模拟无限大实际声场区域，各个域点探针的位置如图19所示。

图19 域点探针分布位置

2.7.2 薄膜型局域共振隔声罩隔声性能分析

在单极子无指向声源的作用下，选用薄膜厚度为0.2 mm，长8 mm，宽4 mm的铝框架的情况下，3种薄膜型隔声罩不同测点处的插入损失曲线如图20所示。

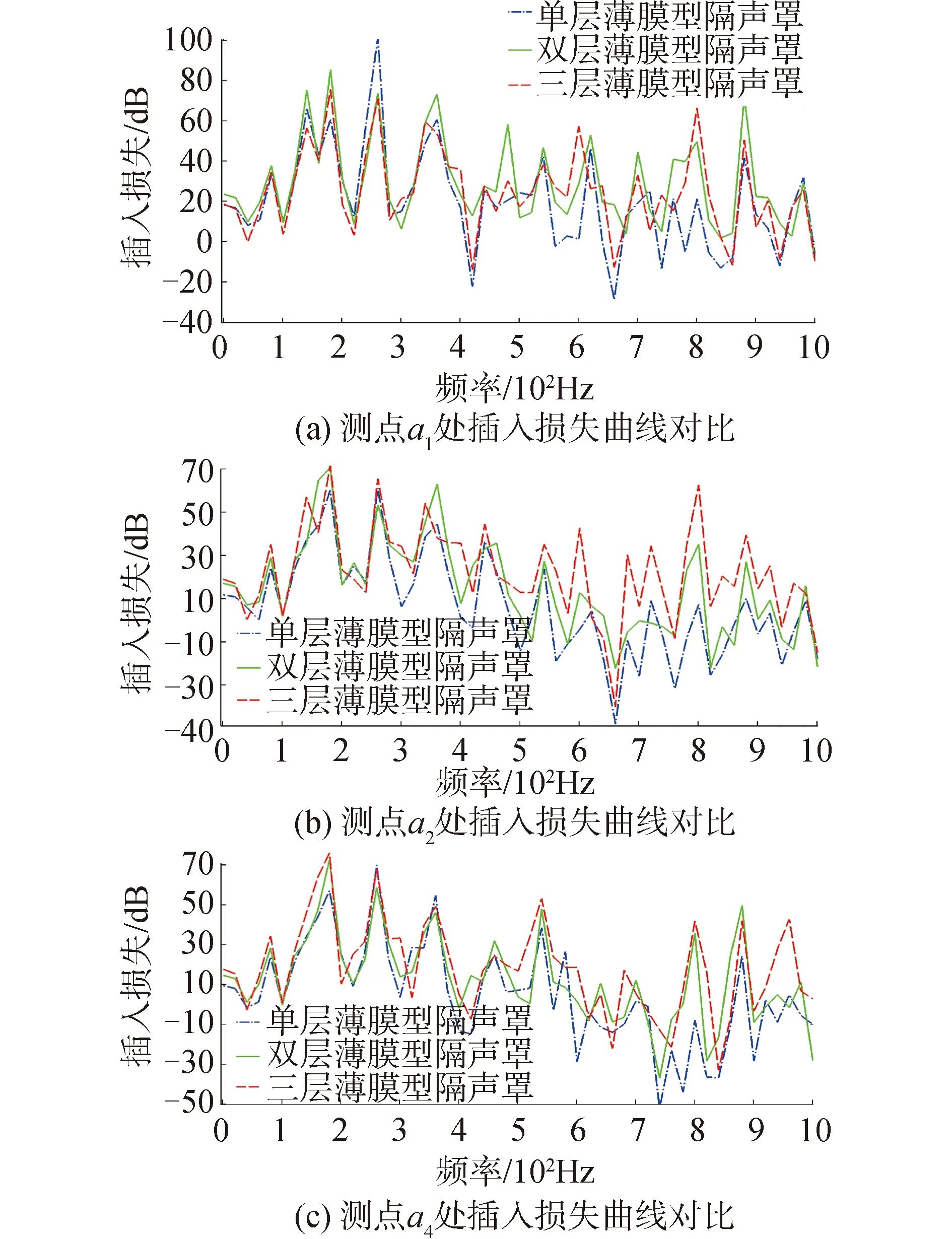
图20 3种薄膜型隔声罩不同测点处插入损失曲线对比

由图20可知，随着薄膜型声学超材料层数的增加，隔声罩各个测点处的插入损失逐渐提高；层数的增加对整个计算频段的隔声性能均有不同程度的提升效果。

2.7.3 薄膜质量块型局域共振隔声罩隔声性能分析

质量块可以增加结构隔声峰的数量，并且能够使隔声低谷向低频移动，下面将分析预应力0.3 MPa下，添加1 g附加质量后的单层薄膜型声学超材料隔声罩的隔声性能，添加附加质量后，各个测点处2种薄膜质量块型隔声罩各个测点的插入损失曲线如图21所示。

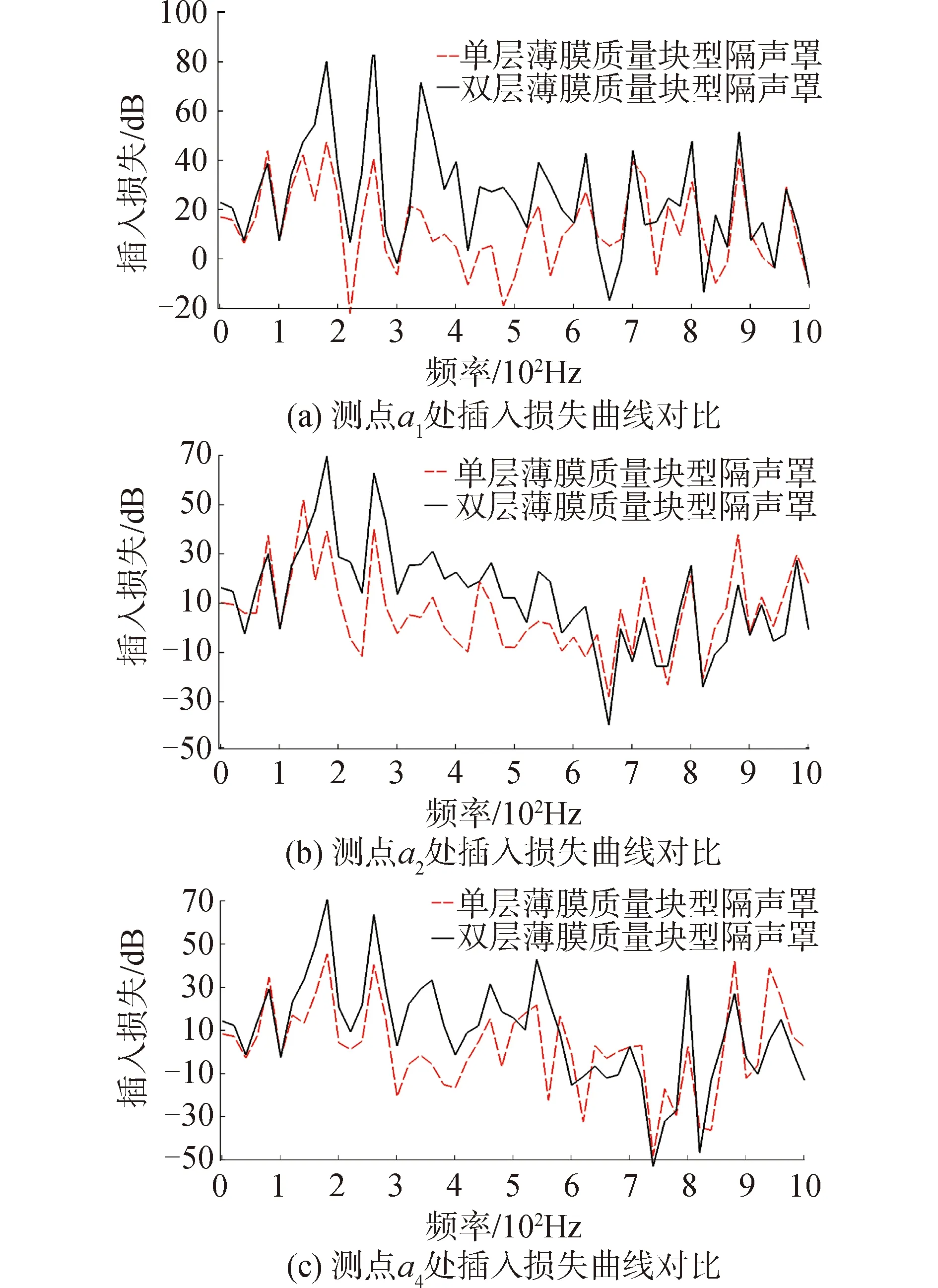
图21 2种薄膜质量块型隔声罩各个测点的插入损失曲线对比

由图21可知，100 Hz以内的单层薄膜质量块型隔声罩隔声性能略高于双层薄膜质量块型隔声罩；100 Hz以后，双层隔声罩的隔声性能远高于单层隔声罩；600 Hz以后2种结构的中频隔声效果很差。在实际工程应用中可以针对特定的需求进行结构设计。

2.7.4 低频宽带局域共振隔声罩隔声性能分析

吸声材料的添加对结构整体的隔声性能有一定的提升效果，在中频段的吸声作用优于低频段。通过前文的分析结果，以3层薄膜型隔声罩为基础，拟在隔声罩空腔中添加不同厚度的吸声材料以改善薄膜型局域共振隔声罩整个计算频段的隔声性能。添加吸声材料后的薄膜型局域共振隔声罩的结构模型如图22所示，图22中3层结构中的黄色空腔为添加吸声材料位置。

图22 3层薄膜型局域共振隔声罩结构示意

薄膜型局域共振隔声罩各个测点的插入损失曲线如图23所示。

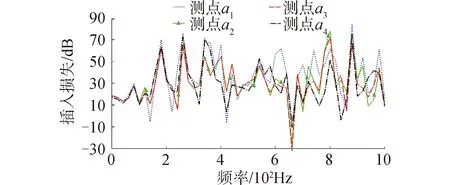
图23 安装3层薄膜型局域共振隔声罩之后各个测点处的插入损失曲线

添加吸声材料以后，在低频段，第1个隔声峰80 Hz处的插入损失为29 dB；最大隔声幅值为75 dB；在200～600 Hz内出现了一个非常宽的隔声带，隔声峰幅值均在35 dB以上；25 dB处的隔声带宽甚至达到了490 Hz(153～643 Hz)；中频段的插入损失对比未添加吸声材料的隔声罩显著提高，各个测点的变化趋势一致，插入损失曲线较为稳定，最大隔声幅值为85 dB。薄膜型局域共振声学结构隔声罩在整个计算频段展现出了优良的隔声性能。

3 结论

1) 在刚度控制区内薄膜型声学超材料的隔声性能要远优于同质量均质材料；附加质量的添加可以降低第1隔声谷和隔声峰频率位置，增加隔声峰幅值，但是隔声谷的位置也会相对提前，导致低频隔声性能有所下降。

2) 针对大尺寸薄膜型局域共振声学结构的隔声问题，基于有限元法建立了周期性小试件模型，由仿真结果可知，相比无附加质量的双层薄膜型局域共振声学结构，质量块增加了系统振动的复杂度，使隔声曲线的隔声峰增多，但是对100 Hz以内频段影响较小；通过计算得到了结构不同材料阻尼和框架刚度下的隔声量。

3) 针对普通局域共振声学结构难以实现宽带隔声的问题，进一步设计了由优化框架结构和填充吸声材料的3层膜结构组合而成的低频宽带薄膜型局域共振隔声罩，由仿真结果可知，80 Hz处的插入损失为29 dB，在200～600 Hz内出现了一个非常宽的隔声带，隔声峰幅值均在35 dB以上；插入损失曲线较为稳定，最大隔声幅值为85 dB，在整个计算频段获得了优异的隔声性能。