复合材料激光超声波传播特性及缺陷损伤检测

付兰凌， 杨金水， 刘志达， 罗浩

(1.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001； 2.哈尔滨工程大学 青岛创新发展基地，山东 青岛 266000； 3.哈尔滨工业大学 复合材料与结构研究所，黑龙江 哈尔滨 150001； 4.洛阳船舶材料研究所，河南 洛阳 471023)

与传统的金属材料相比，纤维增强复合材料具有高比强度、高比刚度、耐磨损、抗腐蚀以及高度可设计性等优异特性，现已广泛应用于航空航天等各个领域[1]。然而，在复合材料的制造和使用过程中，在材料自身属性、生产工艺、服役期间环境及载荷等因素的作用下，不可避免地会产生各类损伤缺陷。复合材料常见的缺陷类型包括基体开裂、界面脱胶、分层和纤维断裂4种基本形式[2]，这些损伤会随着复合材料的使用而逐渐扩展、合并从而形成更大的缺陷，当缺陷超过结构的容损极限后就会导致结构强度的下降甚至失效破坏。因此，在复合材料结构的全生命周期内对其进行损伤检测从而提早发现损伤并对其进行进一步有针对性的修复是十分必要的。现有的复合材料无损检测技术包括目视检测、渗透检测、敲击检测、超声波、CT与X射线、声发射、电阻抗、红外热波等。其中，超声波检测技术由于其具有精度高、无辐射、适用于非导电材料等优点，成为目前应用最为广泛的复合材料无损检测方法[3]。传统的超声检测原理主要利用压电效应和逆压电效应激发和接收超声信号，但需要利用水或高分子凝胶作为耦合剂，难以实现对高温物体的检测且对转角等位置的检测能力也不足。激光超声检测技术具有非接触、不需要耦合剂、可远距离检测、分辨率高等优点，拥有广泛的应用前景[4]。将激光超声无损检测应用于复合材料，可实现对分层缺陷的高精度检测[5]，是复合材料无损检测和性能评估的最有效途径之一[6]。但现阶段复合材料的激光超声检测仍面临2个问题：一是波形复杂性，二是检测过程的大背景噪声和信号的相对微弱[7]，很多问题还需进行进一步系统深入的研究。

White等[8-9]首次观测到激光脉冲在固体和液体中激发出超声波的现象，之后Jalell等[10]将有限元法应用于激光超声激发机理的研究，发现其能较精确地反映超声位移波形，使得有限元法成为重要的研究手段。在激光超声检测方面，周正干等[11]利用激光超声检测系统，分别采用脉冲反射法和透射法对复合材料进行C扫描成像，获取了分层缺陷的多种特征，验证了激光超声检测技术对复合材料分层缺陷的适用性。裘进浩等[12]对激光激励的超声特征信号进行分析，实现了对复合材料脱粘损伤的成像并对其疲劳剩余寿命进行了预测。刘旭等[13]运用有限元法研究了激光激励位置和复合材料编织结构对超声波传播特性的影响。总的来说，现阶段针对复合材料各向异性及多种铺层设计等特点进行的激光激励复合材料超声波传播特性和缺陷检测研究还很少，处于起步阶段。因此，本文基于弹性力学和热力耦合理论，拟建立激光激励下纤维增强复合材料单层及层合结构的完全热力耦合数值仿真模型，系统开展了含缺陷结构的激光超声波传播特性及缺陷识别方法研究。

1 仿真参数设定及可靠性验证

1.1 仿真参数设定

在热弹效应下，复合材料的表面受到激光辐射的作用产生热膨胀，进而产生局部的热应力，应力波在物体内传播并与缺陷发生相互作用，因此可以将应力波作为无损检测的媒介。基于热力耦合基本理论[14]，激光激励的热力耦合方程可由下列方程组表示为：

式中：kij为热传导张量；ρ为材料密度；Q为热源；cv是定容热容量；βij为热耦合张量；T为绝对温度；Ui为位移张量；cijkl为弹性模量张量；fi为体力张量。

复合材料柔度转轴为：

(1)

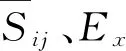
结合复合材料转轴公式，根据各向同性材料的纵波波速公式，可得复合材料各个方向的纵波波速为：

(2)

式中：E为对应方向上的等效弹性模量；v为泊松比；ρ为密度。

基于完全热力耦合理论，运用ABAQUS有限元软件，采用热固耦合-显式动力学分析进行复合材料激光超声传播特性仿真计算，碳纤维复合材料单层厚度为0.25 mm，分别建立平面尺寸为50 mm×50 mm的单层板和层合板数值模型，边界条件设置为4边固支，环境温度为300 K，碳纤维复合材料的材料基本参数如表1所示。

表1 碳纤维增强环氧基复合材料单层板材料基本参数

激光脉冲激励参数在进行仿真时采用如下假设：

1)激光函数的空间分布精确服从高斯分布。

2)激光能量被材料全部吸收，忽略材料热对流和热辐射造成的热量损耗。

激光激发表面热源的等效热流密度为:

q=β(1-R)I0f(x,y)g(t)

其中：

式中：β为材料的光吸收系数；I0为激光脉冲的功率密度；a为激光光斑半径；t0为激光脉冲的脉冲宽度；f(x,y)和g(t)分别为脉冲激光的空间和时间分布函数；R为材料表面反射系数，根据假设2)可知R值为0。

仿真模型的激光光斑半径为1 mm，激光能量为10 mJ，脉冲激励持续时间为10 ns，等效热流密度为3.2×108mJ/(mm2·s)。

本文为保证在满足求解精度的情况下尽量缩短计算时间，在热激励周期内设置1×10-9s为固定时间增量，其余时间段增量由软件自动选取，且最大时间增量不超过5×10-9s。

1.2 网格收敛性分析

通过设置沿复合材料纤维方向上表面距激励中心点5 mm处的节点作为输出点，并分别选取0.1、0.2 mm网格尺寸进行仿真，提取应力信息并绘制曲线图。结果如图1所示，随着网格尺寸的减小，应力曲线逐渐趋于收敛，本文在保证计算精度的同时为节约计算时间选取网格尺寸为0.2 mm。

图1 不同网格尺寸下的应力仿真结果

1.3 可靠性验证

通过式(1)和式(2)预测各方向的应力波波速并与仿真结果相比较，结果见表2。在θ=0°和θ=90°方向上误差较小，在θ=60°处误差最大达到15%，这主要由于碳纤维复合材料性能的非线性导致。为了进一步验证本文所建立的数值仿真模型的正确性和可靠性。选取文献[13]结果进行对照，如图2所示，仿真应力波波峰出现时间和峰值基本一致，且脉冲后残余应力幅值大小相近，仿真结果仅在细节上有所差异。

表2 各方向上波速误差

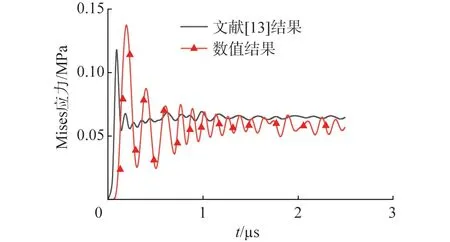
图2 数值结果与文献对比

2 复合材料层合板超声传播特性

2.1 厚度对超声波传播的影响

选取模型上表面几何中心点为激励中心，输出点相对位置及编号如图3(e)所示。选择厚度为0.25 mm的碳纤维单层板，每层均按0°方向铺设，层合板厚度分别设置为0.25、0.5、1和2 mm，计算结果如图3(a)～(d)所示。在点X0Z3处厚度的改变对相位的影响不大，但随着板厚度的增加，波在上下表面之间的传播距离增加，导致应力波震荡频率降低。通过比较不同厚度下点X0Z3和X5Z3、点X0Z0和X5Z0处的应力波曲线，可以发现，信号幅值随着传播距离和板厚的增加而减小。在点X0Z3、X5Z3处，即激励点同侧，输出点应力波的相位几乎不随板厚的变化而产生较大变化。在点X0Z0、X5Z0处，即激励点异侧，输出点应力波的相位随着板厚的增加而出现明显的滞后。综上所述，激励源同侧的的应力波幅值与板厚度呈负相关，应力波相位与板厚无关；对于激励源异侧的应力波幅值与板厚度呈负相关，应力相位随板厚增加而滞后。总体上，应力波幅值与距离成负相关。

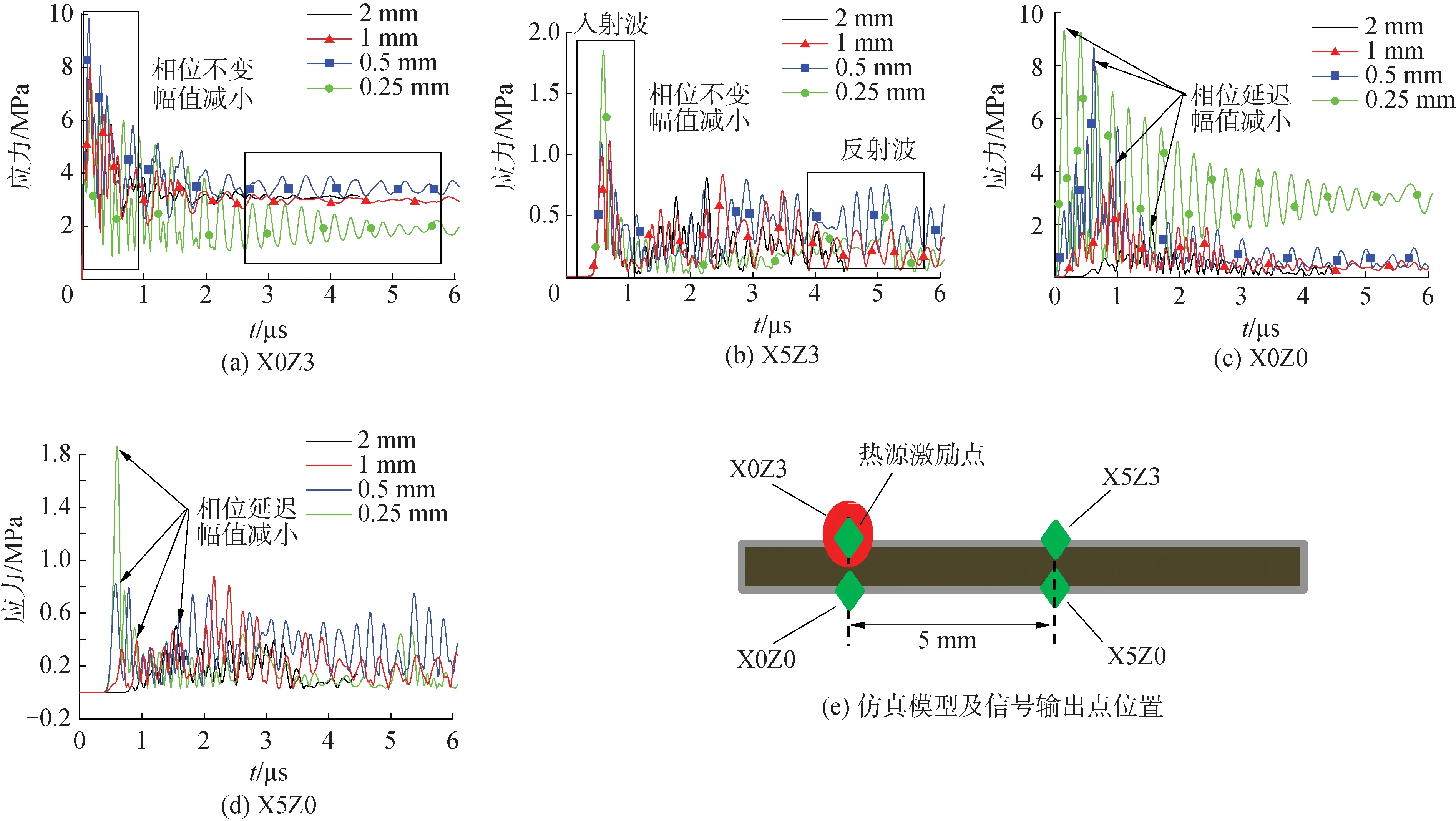
图3 不同厚度下层合板中应力波曲线及其仿真模型

2.2 铺层角度对超声波传播的影响

为研究碳纤维复合材料的铺层角度对超声波传播的影响，设计模型为每层厚度为0.25 mm，共8层，总厚度为2 mm的碳纤维复合材料层合板，铺层角度分别为[0]8、[-45/45/90/0]s、[0/90/45/-45]s，分别命名为lm1、lm2、lm3，输出点的选取和编号与前文相同。如图4(a)～(d)所示，在X0Z3处，应力波信号差异非常小，由此可知在激励点处铺层方式对应力波的影响很小；在X0Z0处，不同铺层角度下曲线的峰值相位较为接近，这表明激励点对心处的应力波相位受激光光源参数和复合材料Z方向的材料性能影响较大，而铺层角度对其影响较小；但不同铺层角度下幅值差异较大；在X5Z3处，表面铺层角度同为0°的lm1和lm3的应力波幅值、相位均相近，而表面铺层为-45°的lm2的应力波幅值、相位均与0°铺层有较大差异，表明对于表面点，应力波的特性主要取决于表面的铺层角度；在点X5Z0处，由于应力波在传播过程中受到各层铺层角度的影响，在幅值和相位上均存在较大的差异。综上所述，在厚度相同的情况下，复合材料应力波在Z方向的传播特性主要取决于单层板Z方向的材料特性，与铺层方式无关；应力波在面内的传播特性主要取决于表面层的铺层方式，而非表面层的铺层方式对其影响较小；应力波的衰减与层铺方式有较大关系，层铺方式越复杂应力波的衰减越明显。

3 复合材料层合板损伤检测

3.1 面内缺陷长度对检测结果的影响

面内损伤仿真模型按图4(e)所示布置，损伤部位使用宽度为1 mm的长条状面内凹槽进行替代，输出点按所处坐标进行编号，分别为X4Y0、X8Y0、X17Y0、X21Y0、X8Y2和X17Y2。缺陷设置为贯穿损伤，长度分别为4、6 mm，各输出点的Mises应力曲线如图5所示，在相同缺陷长度下，X4Y0、X8Y0和X8Y2 3个点位于激励点和缺陷之间，在曲线图中可以发现，有缺陷模型相较于无缺陷模型，出现额外的反射波波峰，且由于缺陷的阻挡边界反射波较弱。X17Y0、X21Y0和X17Y2 3个点位于缺陷外侧，在曲线图中可以发现受缺陷的遮挡，3个输出点的应力波幅值大幅降低，相位大幅滞后，其中距离缺陷更近的点X17Y0和X17Y2，由于受缺陷的遮挡更为严密，幅值的减小和相位的滞后均大于点X21Y0。对比相同缺陷尺寸下Y=0 mm和Y=2 mm处所有点的Mises应力曲线，可发现位于Y=0 mm线上的反射波强度远大于Y=2 mm上的反射波强度。当缺陷的长度由4 mm增加至6 mm时，位于激励点和缺陷之间的点X4Y0、X8Y0和X8Y2，应力波相位基本保持不变，反射波幅值增加。位于缺陷外侧的点X17Y0、X21Y0和X17Y2应力波幅值减小，且相位滞后。

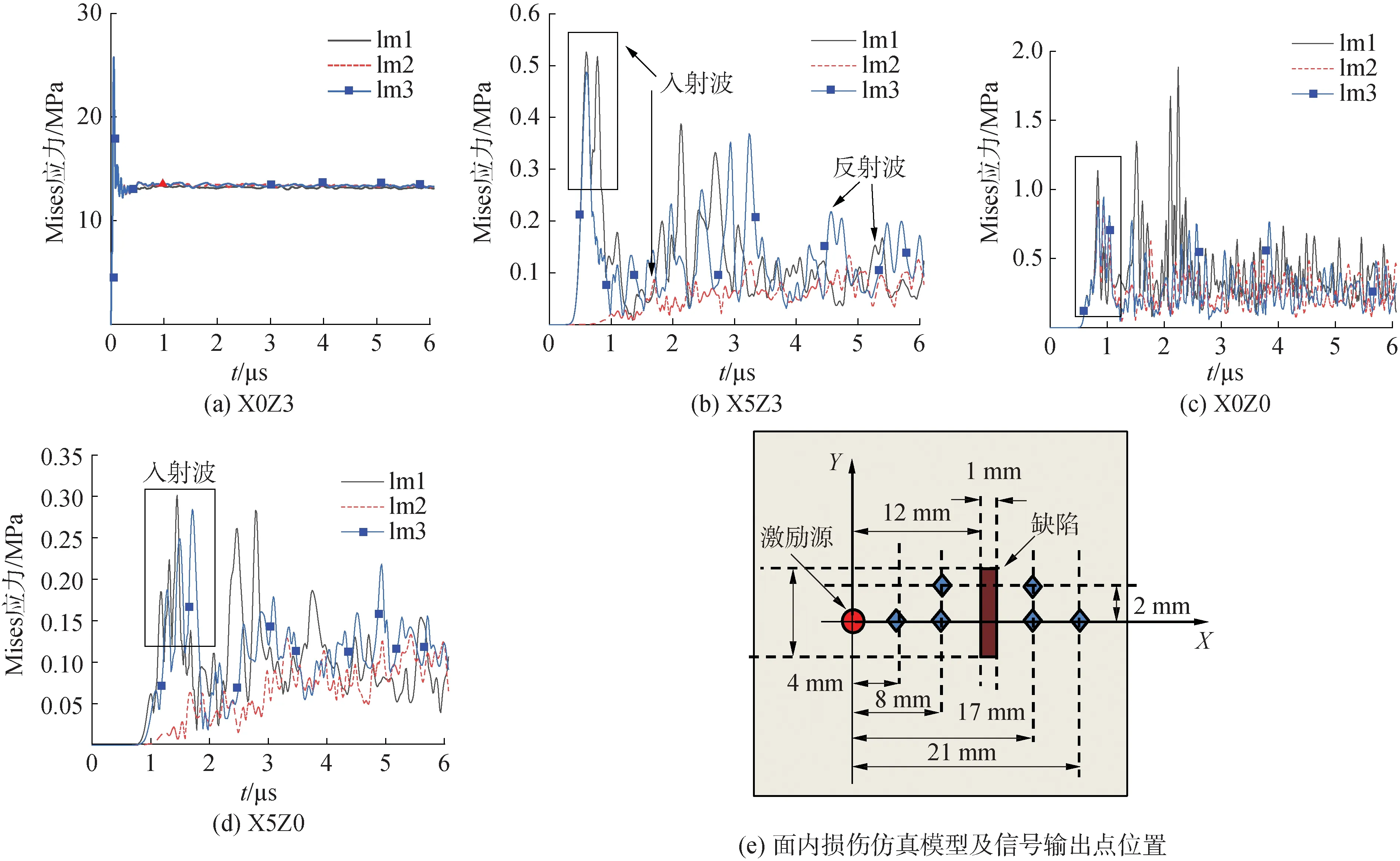
图4 不同铺层顺序下层合板中应力波曲线及面内损伤仿真模型

图5 不同缺陷长度的应力波曲线

综上所述，缺陷反射波的相位与缺陷尺寸无关，缺陷反射波的强度与缺陷尺寸呈正相关；缺陷绕射波的相位和强度与缺陷的尺寸成负相关，距缺陷越近其幅值的减小和相位的滞后越明显；输出点距离面内缺陷中轴线越近其反射波强度越强。因此，当应力波垂直入射时，可选取面内缺陷中轴线上的点作为信号接收点。

3.2 面内缺陷深度对检测结果的影响

缺陷的面内位置及输出点位置和编号与前文相同，缺陷尺寸为6 mm×1 mm，分别设置为贯穿损伤和半贯穿损伤，输出点Mises应力曲线如图6所示。位于缺陷和激励点之间的点，缺陷反射波强度随着缺陷深度的增加而变大，反射波相位基本不变。在缺陷外侧数据点处，由于应力波的传播方式由穿透型裂纹的绕射传播转变为半穿透型裂纹的透射传播，应力曲线的差异较大，半贯穿损伤的透射波强度大于贯穿损伤的绕射波强度，但略小于无损伤模型，半贯穿损伤模型的相位亦稍有滞后。综上所述，相对于半贯穿型裂纹，贯穿型裂纹对于波的反射作用稍强，但是对应力波的阻挡作用大大增强。因此，可利用透射波强度对缺陷深度较为敏感的特性，确定损伤深度。

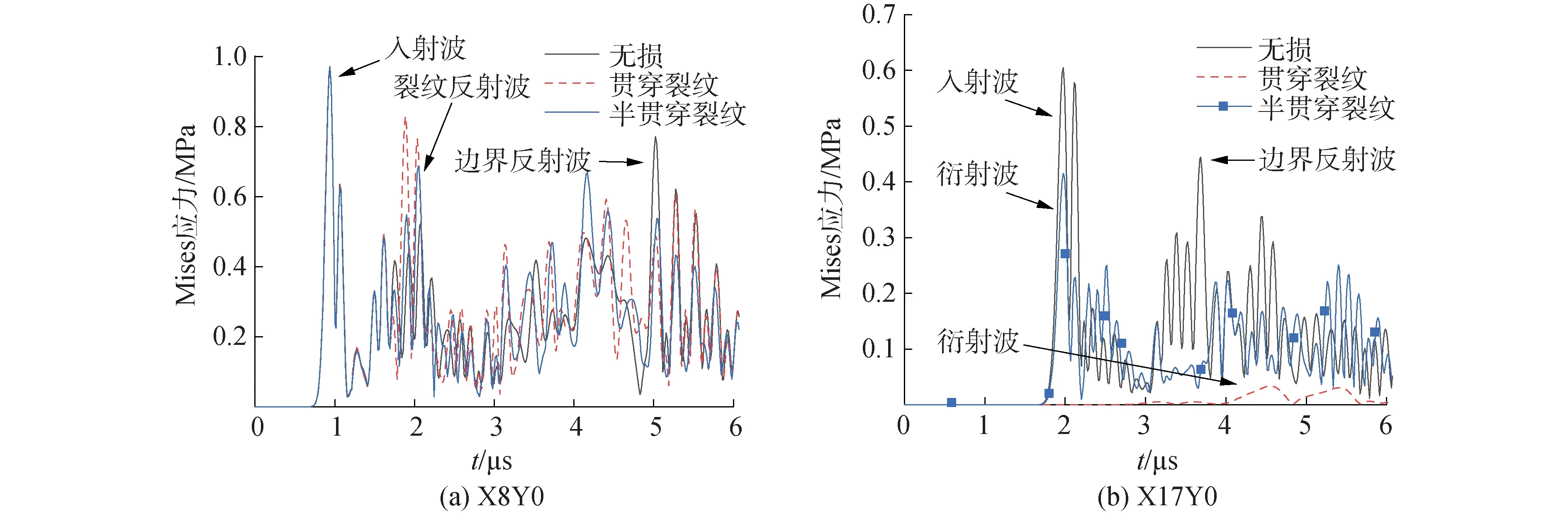
图6 不同缺陷深度的应力波曲线

3.3 分层缺陷对检测结果的影响

设置仿真模型尺寸为50 mm×50 mm×3 mm，分层损伤利用在对应层切割0.1 mm厚的空隙平区域内时，设置分层缺陷尺寸4 mm×4 mm×0.1 mm,缺陷中心正对激励点，缺陷深度分别为0.5、1和1.5 mm。输出点分别位于距激励点0、5 mm的上下表面处，根据坐标编号为X0Z0、X0Z3、X5Z0和X5Z3,其相对位置如图7(e)所示。

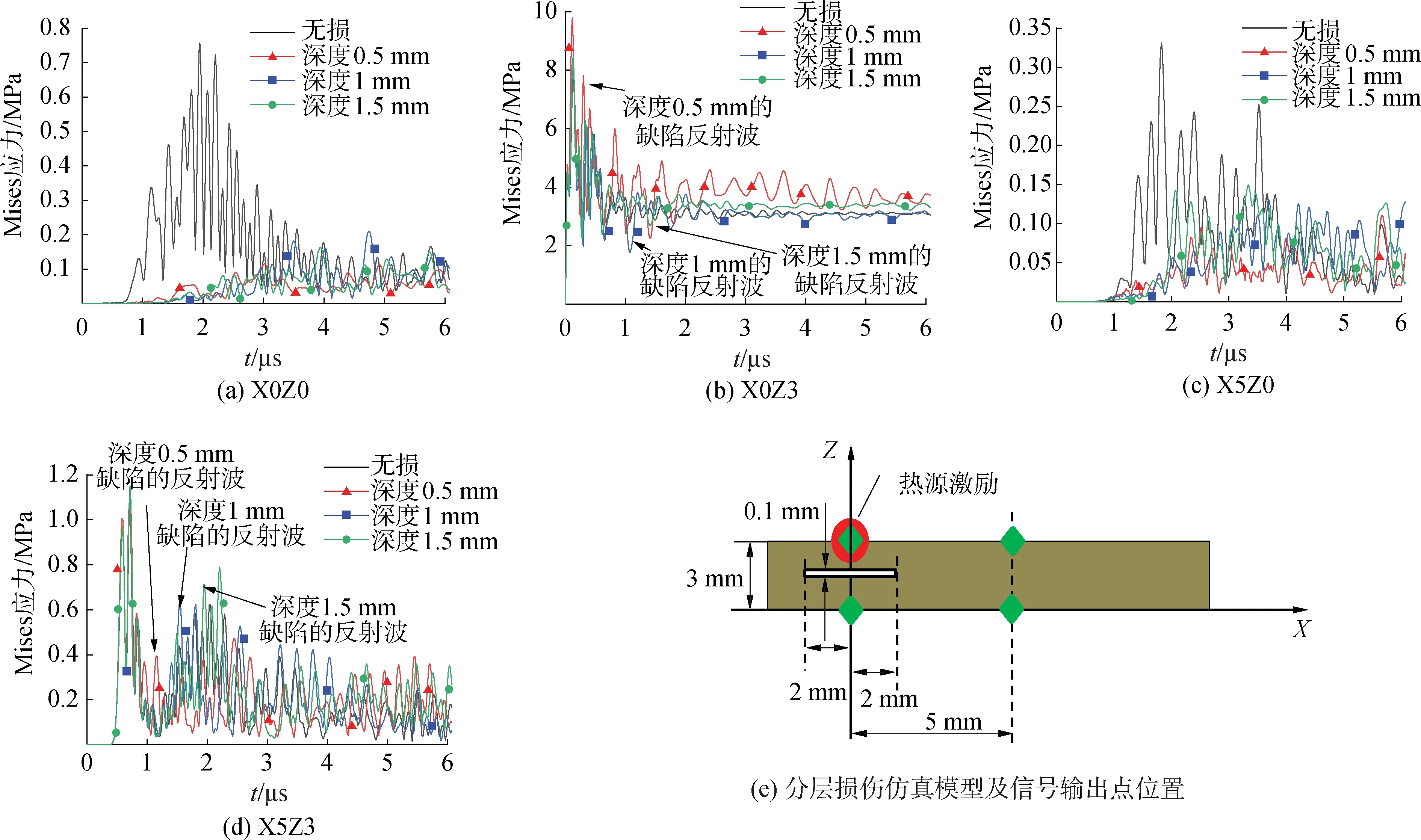
图7 激励点位于缺陷水平面区域内的应力波曲线和仿真模型

各点处的应力曲线如图7(a)～(d)所示，图7中可见位于模型下表面各点，相较于无损模型，分层损伤模型应力波均出现了较大程度的幅值减小和相位滞后，对于被缺陷遮挡的点X0Z0，在不同深度的缺陷下，应力波幅值和相位较为接近；对于未被缺陷遮挡的点X5Z0，缺陷深度越浅，应力波幅值的减弱和相位的滞后的程度越大。对于位于模型上表面的各点，均可以发现反射波波峰。当输出点位于激励点处时，应力波主要沿厚度方向传播，由纵波波速公式得厚度方向纵波波速为2 615 m/s，可确定分层缺陷的深度。

当激励点不在缺陷水平区域内时，设置缺陷尺寸如前，缺陷中心点距激励点5 mm，数据点分别位于X0Z0、X0Z3、X9Z0和X9Z3，模型设置如图8(e)所示。各点处应力波曲线如图8(a)～(d)所示，可发现，位于激励点上下表面输出点的应力波波形均未见明显改变；在缺陷与激励点延长线上的测量点处，下表面点初期应力波曲线与无损伤模型基本一致，之后出现幅值减小；相反地，在上表面点初期应力波曲线与无损伤模型基本一致，之后出现幅值增大。对比激励点位于缺陷上方和位于缺陷侧方的2种情况，可发现当激励点位于缺陷上方时，缺陷反射波强度最大，透射波衰减最为明显。综上所述，缺陷深度与反射波幅值成反比，反射波相位与缺陷深度基本无关；缺陷绕射波幅值与缺陷深度成正比，且深度越浅相位滞后越大。当激励点和输出点越接近分层缺陷水平投影区域时，其反射应力波信号越强，绕射应力波强度衰减越明显。因此，可使用脉冲反射法和脉冲透射法探查分层。

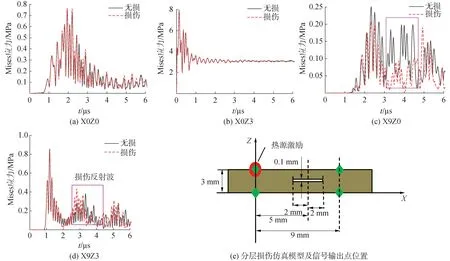
图8 激励点不在缺陷水平面区域内的应力波曲线

4 结论

1)对于碳纤维复合材料单层板，应力波信号的衰减程度与传播距离成正比，不同方向上的衰减程度基本相同。应力波在与材料主方向夹角越大时其速度越低，且呈非线性变化；对于碳纤维复合材料层合板，厚度方向的波速取决于单层材料性质，与铺层方式无关；面内方向的波速主要取决于表面铺层角度，与厚度无关。碳纤维层合板中应力波的幅值随传播距离和板厚的增加而减小。

2)对于复合材料面内损伤，应力波在损伤内侧的上下表面处均有反射回波产生，并且缺陷的存在会对应力波产生遮挡作用。相对于缺陷后的绕射应力波，缺陷反射波受缺陷深度影响较小且会出现明显的反射波波峰，适合于作为材料中是否存在缺陷的评判依据；缺陷衍射波受缺陷深度影响较大，在有基准信号的情况下可以有效判断损伤深度。

3)对于复合材料分层损伤类型，当激励点位于缺陷上方时，缺陷会对应力波产生反射和遮挡作用，在缺陷下方点处不同深度的缺陷对应力波的反射和遮挡作用相似；在缺陷外，下方点处缺陷越浅遮挡作用越强。通过比较，当激励点和接收点位于缺陷正上方和下方时检测效果最佳。