基于逆协方差交叉的分布式航迹融合算法
杜度, 李磊, 袁思鸣
(海军研究院, 北京 101161)
随着综合声呐系统的发展,声呐设备由独立单基阵转向多阵联合。多阵数据融合技术是关键研究内容之一。数据融合结构可分为3类:集中式、分布式和混合式[1-2]。其中,分布式融合结构对数据通信链路的带宽要求较低、扩展性好,具有很高的应用价值。航迹融合是一种分布式数据融合结构,融合的源信息是单声呐阵的局部跟踪航迹。
分布式数据融合算法的研究方向可分为2类:数据相关性已知的情况和数据相关性未知的情况。在相关性已知的条件下,可以得到最优的数据融合算法,而实际的应用中,更多是相关性未知的情况,若不考虑相关性的问题,可能会导致数据融合结果的过度自信,严重的情况会出现融合结果发散,因此相关性未知的分布式融合问题更值得研究。
在数据相关性已知或是假定状态估计误差相互独立并忽略相关信息的情况下,简单航迹融合算法[3](simple fusion,SF) 的复杂度低、易于工程实现。但实际情况下,局部航迹的估计误差通常存在一定相关性,若忽略,则融合结果将出现一定的偏离,极端情况可能会出现融合过度自信,进而导致滤波器的发散,因此该算法存在一定的局限性。
为了获得更好的航迹融合效果,数据相关性不可忽视。针对分布式融合系统中状态估计误差存在相关性的问题,Bar等[4-5]推导了已知互协方差条件下的状态估计融合算法,提出了协方差加权航迹融合算法(weighted covariance fusion, WCF)。在已知先验信息的情况下,协方差加权航迹融合算法将局部航迹的估计误差相关性考虑在内,控制了公共过程噪声所产生的影响,是最小均方误差意义下的无偏最优估计。但计算估计误差的互协方差矩阵需要大量信息,算法的复杂度与计算量提升,数据通信速率要求提高。自适应航迹融合算法(adaptive fusion,AF)使用简单的融合算法结构获得与复杂算法一样的精度。AF算法[6]利用决策逻辑,根据输入的局部航迹,进行决策分析,选择合适的航迹融合算法计算系统航迹。Julier等[7-9]提出协方差交叉算法(covariance intersection, CI),无需估计相关性,可用于任意分布式融合系统。在相关性未知的条件下,该算法是一种满足估计结果一致性的保守算法,其融合结果的精度不低于任意局部结果,且融合过程中无需对相关估计误差进行估计。在此基础上进行改进得到的逆协方差交叉算法(inverse covariance intersection, ICI)[10-11]进一步提高了融合精度,是一种更为有效的航迹融合算法。
在数据相关性未知的条件下,本文以椭球法为研究方向,首先对不同局部航迹进行预处理,其次,研究基于ICI的多阵航迹融合算法,并通过理论分析及基于协方差椭球的几何分析验证了该算法的有效性。同时,本文利用位置均方根误差、状态协方差矩阵及海林格距离结合的航迹融合评价指标,客观全面地对融合算法进行性能分析,避免了单一指标的局限性。
1 航迹融合预处理
对于分布式航迹融合系统,每个局部跟踪系统都建立在其自身合适的坐标系下,在局部航迹上传到融合中心进行航迹融合处理之前需要完成局部航迹到全局航迹的坐标转换,将其统一到同一个坐标系下。
以空间直角坐标系为例,图1中有n个局部跟踪节点,在各自坐标系下,每个局部跟踪节点在某时刻探测得到目标的空间坐标分别为(xi,yi,zi),已知各局部跟踪节点的坐标中心相对于全局系统的空间直角坐标为Oi,其中i=1,2,…,n,系统如图1所示。

图1 航迹融合系统坐标转换示意
每个局部跟踪节点得到的目标坐标转换为全局坐标系下的坐标(x0,y0,z0)为:
(x0,y0,z0)=(xi,yi,zi)+(Oi-O),i=1,2,…,n
如图2所示,由于不同局部航迹跟踪系统的采样频率可能不一致,会造成时间不匹配问题。常用的时间对准方法如最小二乘法和内插法等适用于目标的运动模型为匀速直线运动的情况,对机动目标效果不理想。曲线拟合是一种常见的数据处理方法[12-13],拟合的原则是使原始数据散点均匀分布在拟合曲线的上方或下方,该曲线可以反映出数据的整体分布特点,在某种度量条件下,使拟合函数与原始的数据在总体上的偏差最小。最小二乘法以误差平方和最小化为度量标准,寻找针对数据集的最佳匹配函数[14-15]。为此,本文利用基于最小二乘的曲线拟合算法进行时间对准。

图2 采样频率不同下的时间对准问题
假设待拟合的数据集为(xi,yi),利用该数据集拟合后的曲线方程为f(x),则该拟合曲线与原始数据集的误差为:
δi=f(xi)-yi,i=1,2,…,n
拟合函数的形式有很多,一般选择多项式作为拟合函数,设一组线性无关的函数集合为φ={φ0,φ1,…,φn},令:
f(x)=a0φ0(x)+a1φ1(x)+…+anφn(x)=
在最小二乘准则下,曲线拟合的核心公式为:
下面对基于曲线拟合的时间对准算法进行仿真分析:假定目标0时刻由位置0沿着X轴做匀加速直线运动,初速度为1 m/s,加速度为1 m/s2,设定有2个跟踪系统同时开机对目标进行航迹跟踪,系统1的采样周期为3 s,系统2的采样周期为5 s。对跟踪系统1的航迹结果利用二次多项式进行曲线拟合,而后依据跟踪系统2的采样频率进行时间对准,对准前后对比图如图3所示。
由图3中可知,利用曲线拟合的方式可以有效地完成时间对准。

图3 基于曲线拟合法的时间对准
2 基于ICI的多阵航迹融合算法及性能分析
首先,对任一局部航迹状态向量x以及协方差矩阵P,定义协方差椭球:
xTP-1x=c
(1)
式中c为常数。则满足式(1)的所有点构成的轨迹为协方差椭球。当状态向量为二维时,协方差椭球变为协方差椭圆。


ICI算法在CI算法基础上衍生而出,相比于CI算法,ICI算法在满足一致性估计的条件下,可以获得不那么保守的融合结果。ICI算法的融合公式为:
x=Ω1x1+Ω2x2
ω∈[0,1]
其中:
(2)
与CI算法的处理方式类似,由于矩阵对角线元素代表着状态向量估计的方差值,则以协方差矩阵的迹为最小化性能指标,搜索最优权值ω,有如下函数:
(ωP1+(1-ω)P2)-1)-1
(3)
接下来,对逆协方差交叉算法性能进行理论分析。首先给出一个引理[16]:对于任意的权值ω*∈[0,1],一定存在一个权值ω′∈[0,1],使PICI(ω′)≤PCI(ω*)。
假设权值ω′∈[0,1]、ω*∈[0,1],且ω′=1-ω*,根据协方差交叉及逆协方差交叉算法,可推出:
(4)
式中:P1和P2存在对角化矩阵,即:Λ1=AP1AT、Λ2=AP2AT,则式(2)可改写为:
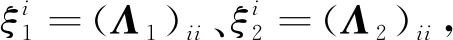
其中:
(5)
则式(4)可表示为:
又因为:
(1-ω*)2+(ω*)2+2ω*(1-ω*)-1=0
(6)
可以推出对角线元素(Λ)ii≥0,从而证明如下关系:
对应得到:
PICI(ω′)≤PCI(ω*)
由式(5)可知,ICI算法的融合精度高于CI算法。
3 航迹融合性能评价指标
为了更加全面地对航迹融合算法进行性能分析,避免仅利用位置均方根误差等单一性能指标的局限性,借助于航迹融合评价指标的思想[17-19],利用不同评价指标融合性分析,以给出合理的数值。
1)位置均方根误差。

式中N代表航迹中的样本总数。
2)状态协方差矩阵。

状态估计协方差矩阵Pk为:
①数值表示法:利用状态协方差矩阵的对角线元素反映目标状态中每个参数估计的误差大小,因此状态估计协方差矩阵Pk的迹可以反映出目标状态估计的精度,记作trace(Pk);
②几何表示法:即协方差椭球,若位置状态向量为二维,协方差椭球退化为协方差椭圆,椭圆越小表明测量精度越高。
下面从几何角度对比分析CI算法和ICI算法的性能,即利用协方差椭球对比分析。设一个二维状态向量的2个状态估计值的协方差矩阵分别为P1和P2,其中:
得到的融合结果如图4所示。由图4可知,从几何角度看,2种融合算法均可以得到精度更高的融合结果。但ICI算法的协方差椭圆始终在CI算法协方差椭圆的内部,ICI算法相比于CI算法有着更高的融合精度。几何分析验证了式(6)推导结果的正确性。
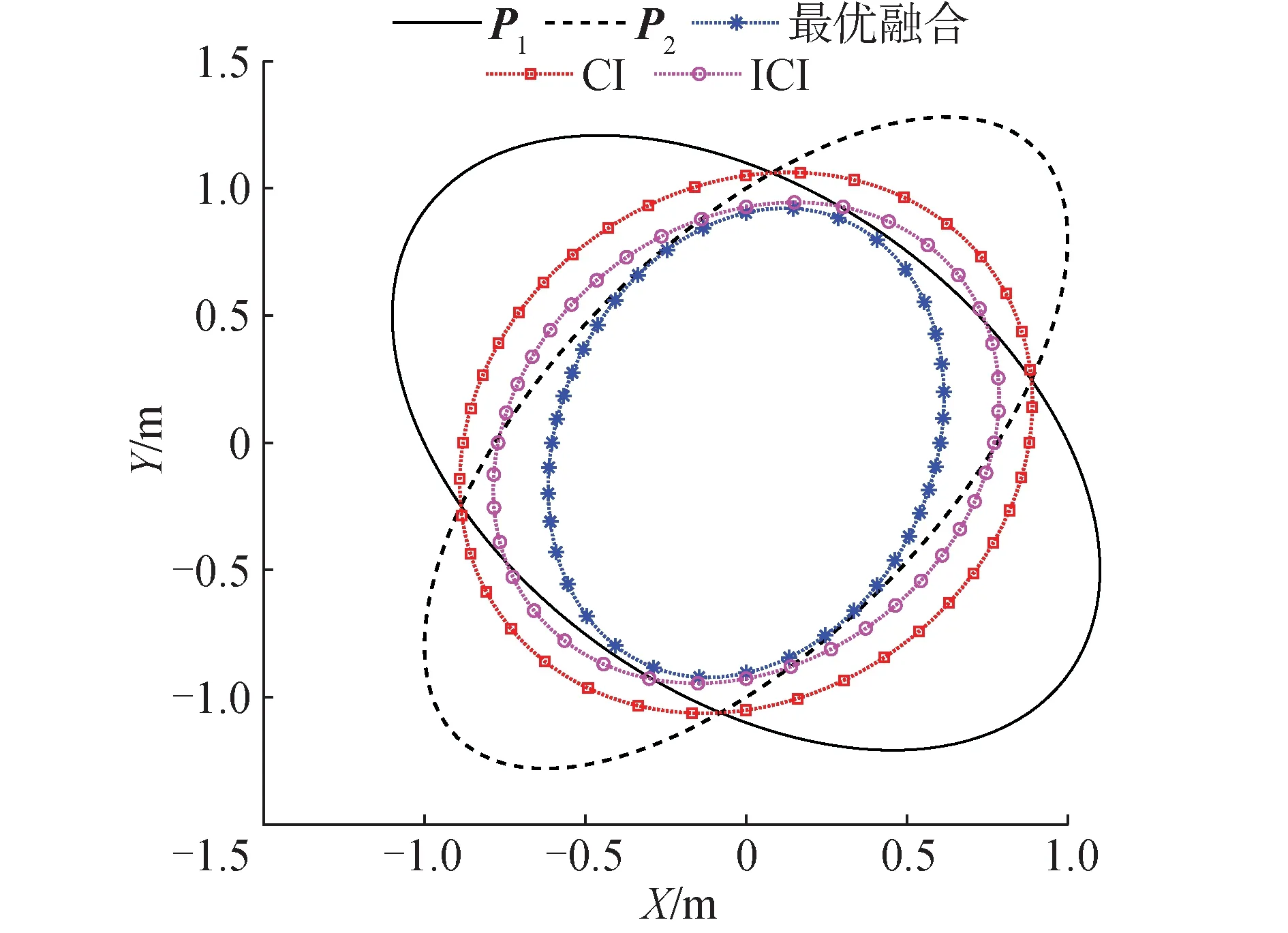
图4 协方差交叉与逆协方差交叉融合结果对比
3)海林格距离。
位置均方根误差在一定程度上可以有效地反映出融合算法的优劣性,但是没有将估计状态的不确定性考虑在内。状态估计的协方差矩阵反映了估计结果的不确定性,因此有必要将其考虑到融合算法的性能评价指标内。
举例说明海林格距离,假设某目标的真实状态为μ=(0,0),有3个状态估计结果如表1所示。

表1 状态估计结果
各个估计状态的均值及其协方差椭圆的分布情况如图5所示。
在概率论与数理统计领域,海林格距离用于度量2个概率分布的相似性。假设存在2个概率分布函数分别为f(·)和g(·),海林格距离定义为:

(7)
对式(7)进行平方项展开,可得:
由柯西-施瓦兹不等式可知,海林格距离的取值范围在0~1,当2个概率分布互相不重叠时,海林格距离得到1。

其中:

表2 RMSE和海林格距离
因此仅仅利用单一评价指标有失偏,同时利用各评价指标,从不同维度评价航迹融合的性能更为公允可靠。
4 ICI算法性能仿真验证
本节设计一个基于被动声呐的航迹估计与融合系统,对ICI算法进行仿真分析。基于被动声纳的分布式航迹融合系统结构如图6所示。

图6 基于被动声呐的分布式航迹融合系统结构
系统存在2个局部跟踪节点,目标运动模型采用“当前”统计模型,跟踪滤波算法采用卡尔曼滤波算法,融合中心采用ICI算法进行处理,融合方程中最优权值“ω”的搜索采用黄金分割法进行求解。
仿真参数如下:
1) 目标运动参数:2次机动运动模型,运动参数如表3所示。

表3 2次机动的目标运动模型参数
2) 量测参数:2部被动声呐提供给跟踪滤波的量测参数为目标的二维坐标x、y,其测量误差服从均值为0 m、标准差为100 m的高斯分布。
3) 目标运动模型:在“当前”统计模型中,机动频率α=0.02 s、最大加速度amax=0.3 m/s2。
图7 (a)给出单次仿真的真实航迹、2条局部跟踪航迹及ICI算法融合后的航迹结果,图7 (b)给出了x及y方向的跟踪误差及融合误差。

图7 ICI算法单次航迹融合结果
图8统计了500次蒙特卡罗仿真下ICI数据融合前后的误差对比。图8(a)给出了x方向和y方向融合前后的位置均方根误差,图8(b)给出了融合前后航速的均方根误差。
表4统计了100~700 s内空间位置均方根误差及航速均方根误差的平均值。

表4 100~700 s内空间位置均方根误差均值
通过图8及表4的仿真结果可以看出,ICI算法综合了局部传感器的状态估计结果,能够有效地给出航迹融合结果。从均方根误差指标评价角度来看,ICI算法融合后的x、y方向误差分别为28.47 m和28.72 m,航速误差为1.60 m/s,均优于融合前的局部航迹。
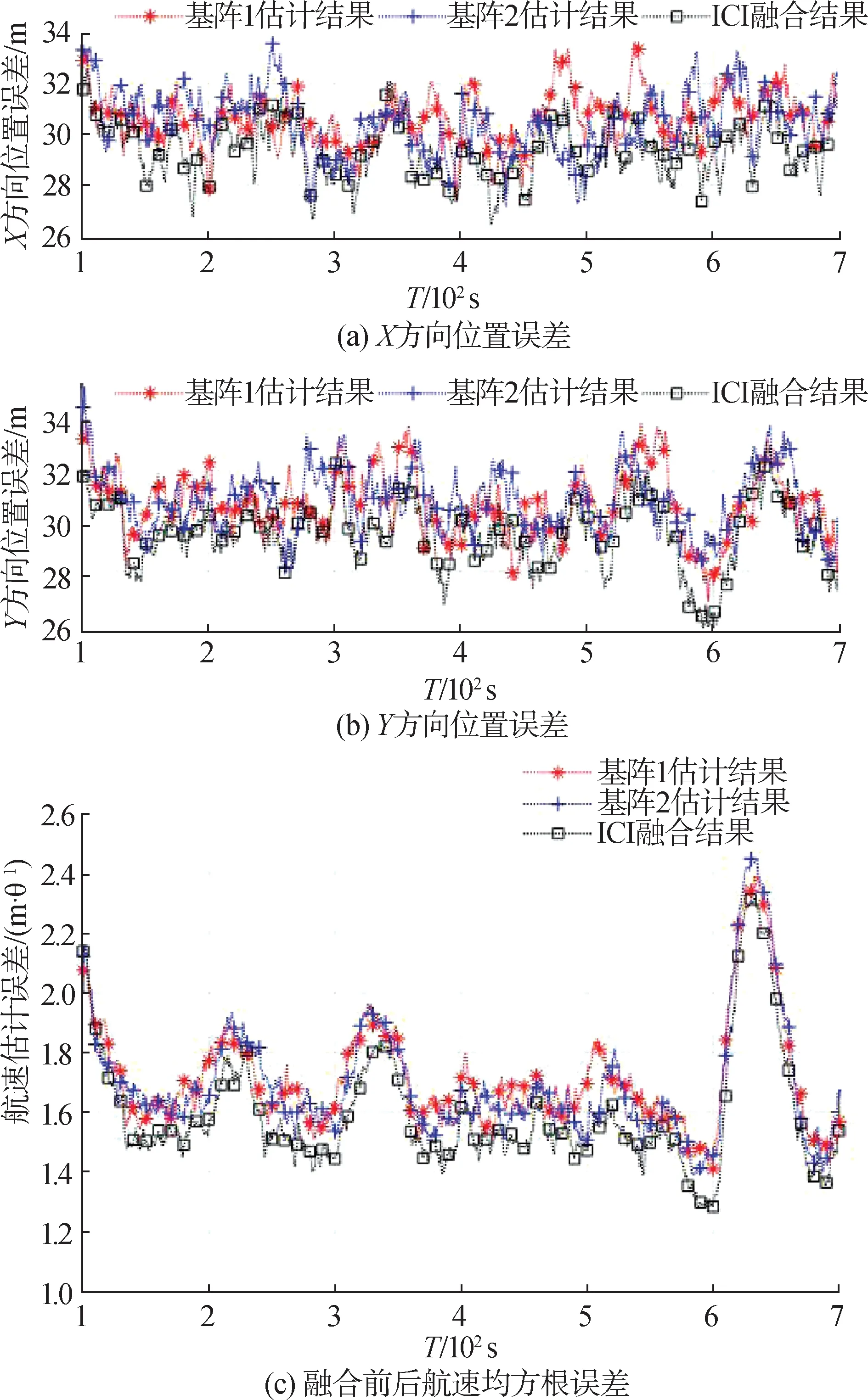
图8 ICI算法航迹融合均方根误差
图9给出了每秒局部航迹及系统航迹的状态误差协方差矩阵的迹的均方根。由图9可知,ICI融合后的状态误差协方差矩阵的迹的均方根始终小于局部航迹,误差值更小,融合后的航迹更加接近真实航迹。

图9 数据融合前后状态估计方差矩阵的迹
接着,利用序贯滤波处理思想,估计得到最优航迹融合结果,而后计算局部航迹状态估计与融合航迹状态估计结果与最优航迹融合之间的海林格距离,如图10所示。
从图10中可以看出融合航迹的海林格距离小于局部航迹,全局航迹的状态估计性能更优于局部航迹。

图10 航迹融合前后海林格距离对比
综合以上仿真结果可知:ICI算法可以有效地对2个独立跟踪节点上传的航迹数据进行数据融合,通过ICI融合可以得到更高精度的结果,且融合过程中不需要进行互协方差矩阵的推导及估计,避免了计算未知互协方差的步骤,对于无法有效估计互协方差的复杂系统结构,算法的适用性及鲁棒性也更高。
5 结论
1)本文考虑到估计误差的相关性对分布式融合的影响,首先对不同局部航迹进行了预处理,研究了基于逆协方差交叉的航迹融合算法,利用不同航迹融合评价指标(位置均方根误差、状态协方差矩阵及海林格距离)结合分析算法性能,避免了单一指标的局限性。
2)理论定量分析与仿真结果说明ICI算法可有效融合不同的局部航迹,且相较于CI算法,融合精度更高。
3)在局部状态估计误差相关性未知的情况下,ICI算法无需计算传感器之间的相关估计误差以及互协方差矩阵,是一种有效的融合算法。同时,融合不同性能指标的评价体系可应用于任意复杂的分布式融合系统中,能给出更为客观公允有效的结果,具有很高的应用价值。

