极端工况静压支承转速与承载力的耦合与协同

于晓东， 黄殿彬， 韩飞， 孙帆， 王发坤， 詹士伟， 周德繁

(哈尔滨理工大学 机械动力工程学院 先进制造智能化技术教育部重点实验室, 黑龙江 哈尔滨 150080)

液体静压支承具有工作速度范围广、运动精度高、摩擦系数和驱动功率低、工作寿命长、良好静动刚度、吸振性能和稳定性等一系列优点，被广泛运用于重型机械、航天航空和军事装备上，成为一种重要支承和传动形式。根据高速重载切削技术需求，被加工零件尺寸和质量越来越大，对静压支承转速和承载提出更高要求，极端工况下如何确保旋转速度和承载能力的协同匹配成为有待解决难题。

何奎霖等[1]研究了极端工况下水润滑轴承摩擦副的摩擦磨损性能，确定了摩擦磨损性能与转速和压力变化关系。于晓东等[2-3]对极端工况下静压推力轴承的动态特性、承载性能的动压补偿等方面进行了深入研究，实现了静压损失的动压补偿，为承载力提高提供了方法。李正等[4-5]模拟水润滑斜-平面推力轴承承载能力，确定最小膜厚、几何参数及转速对轴承承载力的影响规律。杨建玺等[6]获得了静压轴承承载能力与油腔深度的关系，得出浅油腔结构动静压轴承承载能力比深油腔承载力提高了17%的结论，为动静压轴承承载力提高提供了有效途径。岳广杰[7]获得了润滑油粘度、入口流量、封油边间隙、壁面转动速度和边界滑移等因素对油腔中流场结构、速度分布和壁面压强分布的影响。夏龙飞[8]利用静力学平衡方程和导轨处弹性变形流固耦合模型分析了弹性变形对油膜压力分布和承载能力的影响，给承载力综合求解提供了新思路。史霄[9]建立了静压转台支承系统的有限元模型，将静压油膜等效为非线性弹簧单元，考虑转台变形与油腔压力耦合影响，获得了油膜温升对转台承载力的影响规律，虽未考虑转速对承载力的影响，但为问题解决提供新思路。Guo等[10-12]发现复合滑移使轴承动压承载力和动力学稳定性显著提高，为转速和承载力关系的研究提供了借鉴。于晓东[13]研究了扇形腔及圆形腔静压推力轴承润滑性能的速度特性，未涉及极端工况。刘志峰等[14]在考虑离心力情况下推导了极坐标下雷诺方程和能量方程，采用有限差分法求解了不同旋转速度时油腔温度分布与承载性能的关系，但也未涉及高速重载极端工况。赵永胜等[15-16]将静压油膜近似为非线性弹簧单元，实现了重型数控机床定量闭式静压转台变形与油垫承载力耦合求解，同时考虑油膜温升对转台承载力的影响，但未涉及旋转速度和承载力的耦合关系。谢黎明等[17]建立了静压导轨间隙油膜有限元模型，计算了铣车复合加工中心在车和铣工况下油膜刚度，仅仅得到了切削轴向分力和工件重量对油膜刚度和油膜厚度的影响规律。张艳芹等[18-19]揭示了高速静压支承热油携带现象并提出热油携带因子概念，得出热油携带因子受转速影响较大的结论，而未谈及旋转速度和承载能力的关系。Liu等[20]仅仅研究了转速和偏心对高速水润滑静压推力轴承的温升特性，而未涉及承载力性能。孙吉昌[21]分析得出双矩形腔静压滑动轴承压力损失的主要原因为温升引起的液压油粘度下降、转台转动引起的流量损失和压力变化，但未讨论转速和压降的关系。刘超[22]对比了双矩形腔多油垫高速静压推力轴承中心加载与偏载工况的润滑性能，发现偏载过大将导致摩擦学失效。

根据对国内外有关研究文献分析可知，对于极端工况静压支承转速与承载能力协同匹配研究未见报道。本文以双矩形腔静压支承为研究对象，采用模拟仿真、理论计算和实验验证相结合方式，依据摩擦学和润滑理论推导转速和承载能力的协同匹配关系式，模拟静压支承油膜温度场与压力场的载荷和转速特性，最终确保静压支承转速和承载能力的协同匹配，并提出增加承载能力和提高旋转速度合理化建议。

1 静压支承工作原理及结构

旋转速度和承载性能是评价静压支承的2个重要指标,是一对相互制约的耦合因素。静压支承在旋转速度一定时所能承受最大载荷的工况，或其在一定承载时所能达到的最高旋转速度的工况，即为静压支承的极端工况，体现PV值恒定。本文即在此工况条件下开展旋转速度和承载能力的耦合与协同关系的研究。

静压支承工作原理如图1所示，借助液压供油系统，将压力润滑油强制地注入静压支承摩擦副间的油腔，利用油腔封油边和导轨间的阻尼作用，形成静压承载力，将工作台浮升并可以承受一定的外载荷[23-25]。静压支承系统如图2所示，油腔结构尺寸如图3所示。

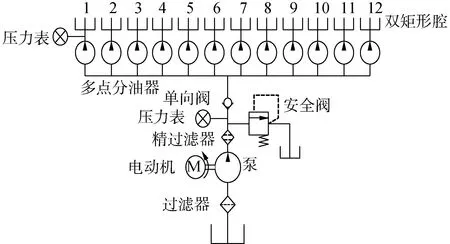
图1 静压支承工作原理

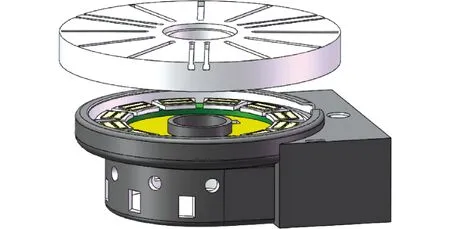
图2 静压支承系统

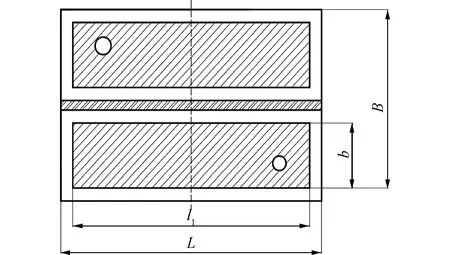
图3 油腔结构尺寸

2 转速与承载能力协同匹配数学模型

2.1 摩擦力矩计算

旋转工作台运动时，因剪切油膜所必须克服粘性阻力为：

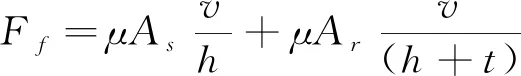
(1)

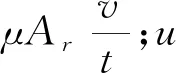
克服粘性阻力所消耗摩擦力矩为：

(2)

式中：z为油垫个数；ω为旋转工作台转速；因导轨宽度相对于其直径很小，故r可近似为油腔中心到导轨回转中心的距离。

2.2 摩擦力矩与转速和载荷关系

导轨有效承载面积Ab为：

(3)

空载时，在工作台自重W0作用下，设计油膜厚度为h0，油腔压力为：

(4)

满载时：

(5)

一个油垫流量：

(6)

导轨油腔间隙：

(7)

根据式(1)～(7)可推出摩擦力矩与载荷和旋转转速的关系为：

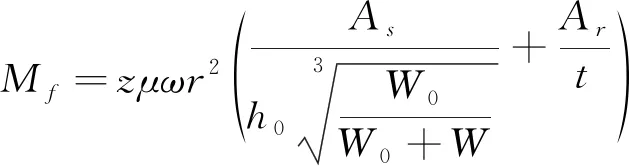
(8)

2.3 转速与载荷协同匹配关系

电动机输出扭矩为：

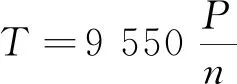
(9)

式中：P为电动机的额定功率，kW；n为电动机额定转速，r/min。

电动机与工作台之间经过多级齿轮变速之后，工作台的输出扭矩为：

T1=ηT

式中η包括联轴器效率、齿轮传动效率、轴承效率和装配效率等。

根据工作台输出扭矩等于间隙油膜内摩擦力矩，即得转速与载荷之间匹配关系为：

(10)

2.4 实例分析

双矩形油腔油垫长为456.2 mm，宽为253.2 mm，油腔长为434.2 mm，宽为99.6 mm，进油孔直径为15 mm，工作台自重为19 t，电动机额定功率为75 kW，转速为1 600 r/min，根据式(10)得到工作台旋转速度与承载能力关系如表1所示。

表1 极端工况时承载能力与旋转速度理论匹配关系

3 油膜温度与油腔压力的载荷和转速特性

根据表1获得的极端工况时承载能力与旋转速度理论匹配关系，模拟极端工况下双矩形腔静压支承的微间隙油膜温度场和油腔压力场的载荷与转速特性。

3.1 微间隙油膜模型

依据双矩形腔静压支承系统结构，抽取支承摩擦副间的微间隙油膜模型，如图4所示。

图4 双矩形腔油膜模型

3.2 微间隙油膜网格划分与边界条件

为提高微间隙油膜温度场和油膜压力场载荷和转速特性模拟分析的准确性，采用六面体非结构化网格对微间隙油膜网格进行划分，并利用O-grid及boundary layer提高网格质量，并考虑Orthog.Angle、Exp.Factor与Aspect Ratio的影响[26-35]。

微间隙油膜入口边界为IN-1和IN-2，质量入口、外侧封油边为压力出口边界OUT-1、OUT-2、OUT-3和OUT-4，出口压力为大气压，与旋转工作台接触的壁面设置为旋转面ROTATE，相邻油腔连接处为周期边界条件INTERFACE1与INTERFACE2，其余部分定义为WALL，油膜形状及边界条件设置如图5所示。润滑介质为46#液压油，其密度为880 kg/m3，比热容为1 884 J/(kg·K)，动力粘度为0.036 5 Pa·s，热导率为0.132 W/(m·K)，摩尔质量为450 (kg·K)/mol，初始温度为20 ℃。

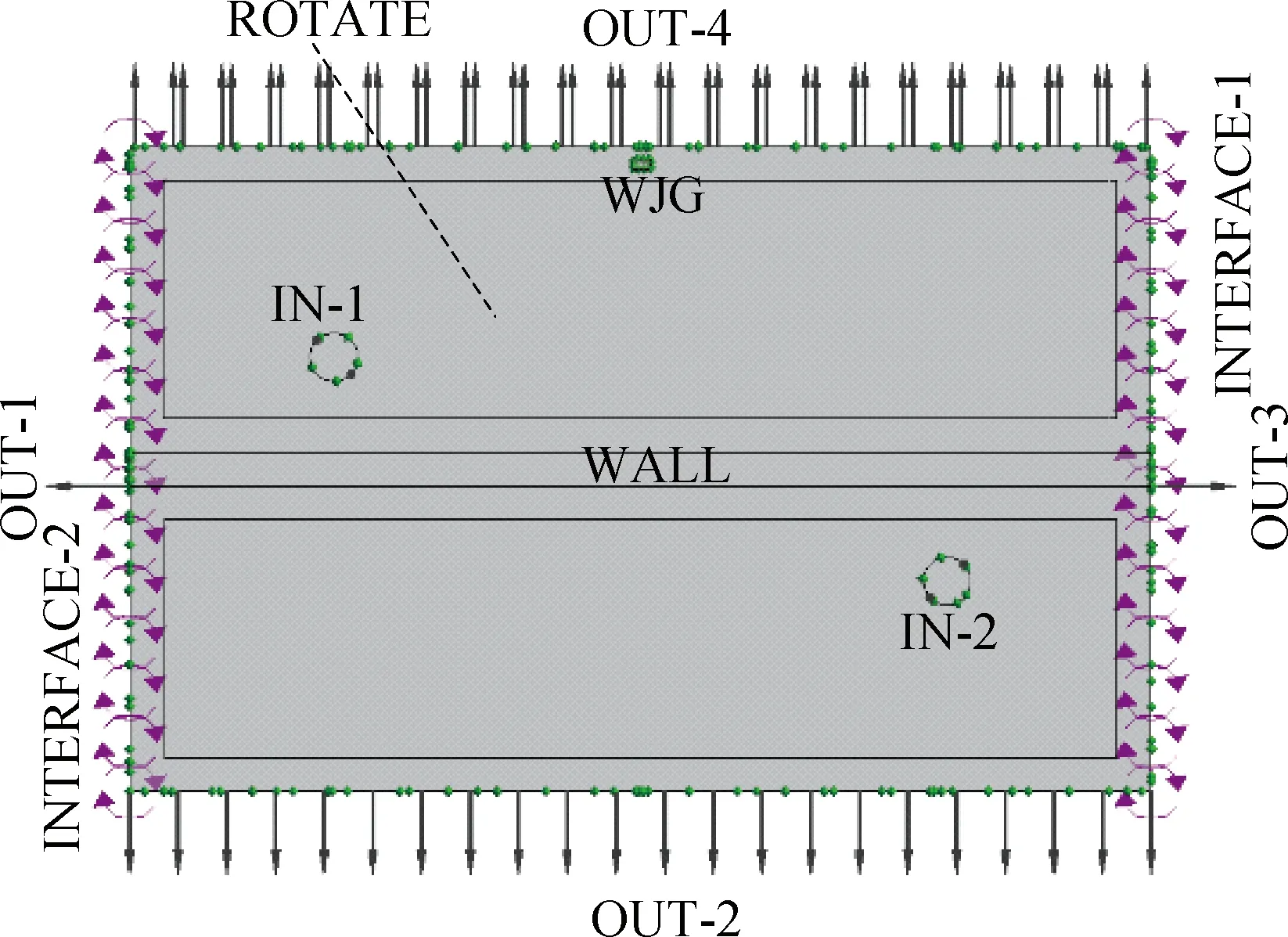
图5 油膜边界条件

3.3 载荷对油膜温度和压力影响

对双矩形腔静压支承在10 t～135 r/min极端工况时的润滑性能进行分析。为研究油膜压力场和温度场的载荷特性，在工作台旋转速度为135 r/min，对不同载荷下压力场和温度场进行数值模拟，承载5 t和10 t时压力场和温度场如图6和图8所示，其他工况模拟数据如表2所示。

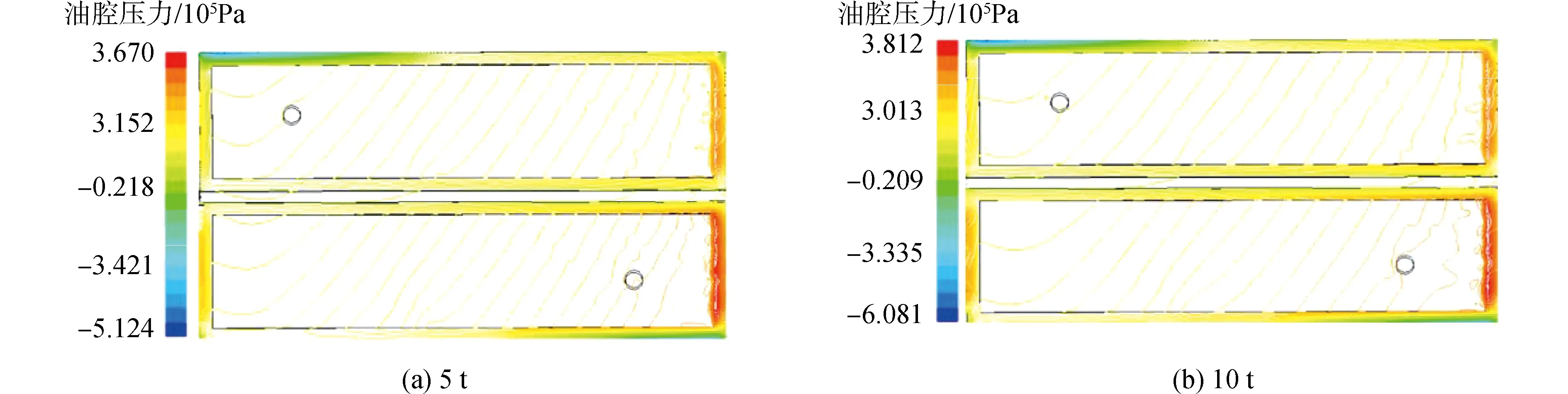
图6 135 r/min时油膜压力场

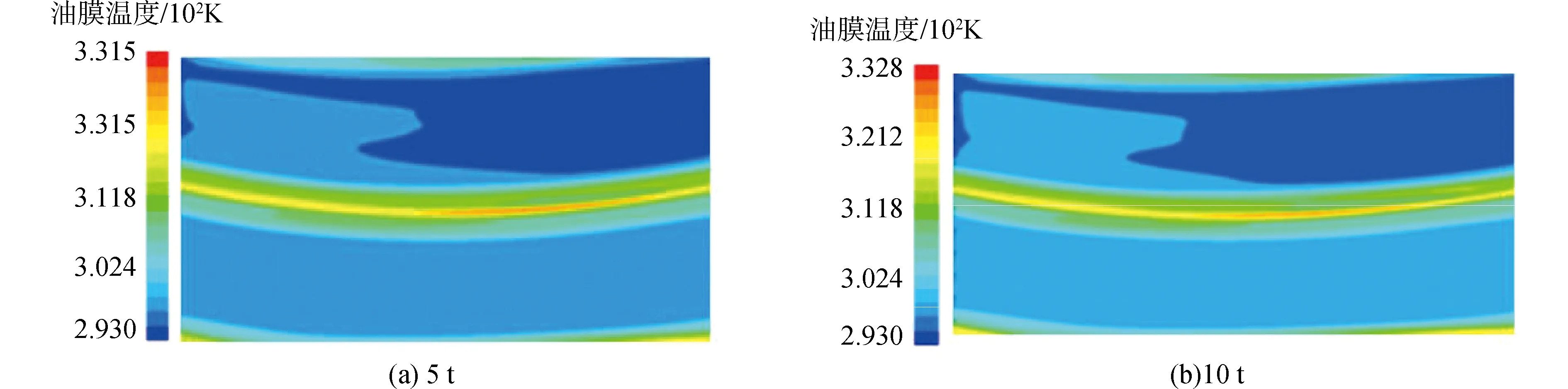
图7 135 r/min时油膜温度场

根据表1可知，工作台转速为135 r/min时对应的极端载荷为10 t。由表2可得，随载荷增大，油膜压力场基本呈线性增加，而油膜温度在承载20 t以内线性增加，超过20 t以上油膜温度增加变缓。

3.4 转速对油膜压力和温度性能影响

同样模拟极端承载10 t载荷时不同转速的油膜压力和温度场，转速135 r/min时压力场和温度场如图8所示，其他工况模拟数据见表3。

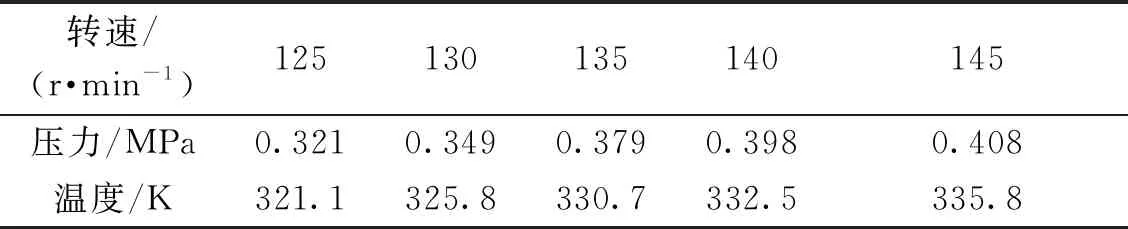
表3 10 t载荷时不同转速的油膜压力场

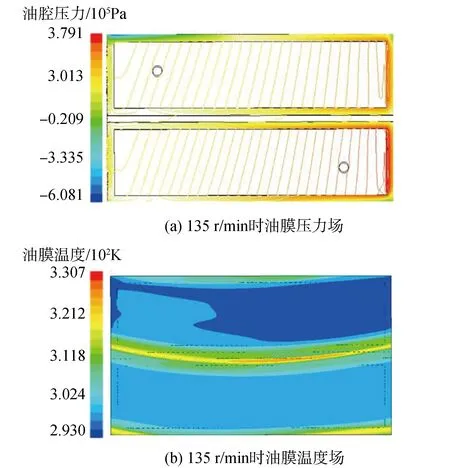
图8 135 r/min时油膜压力场和温度场

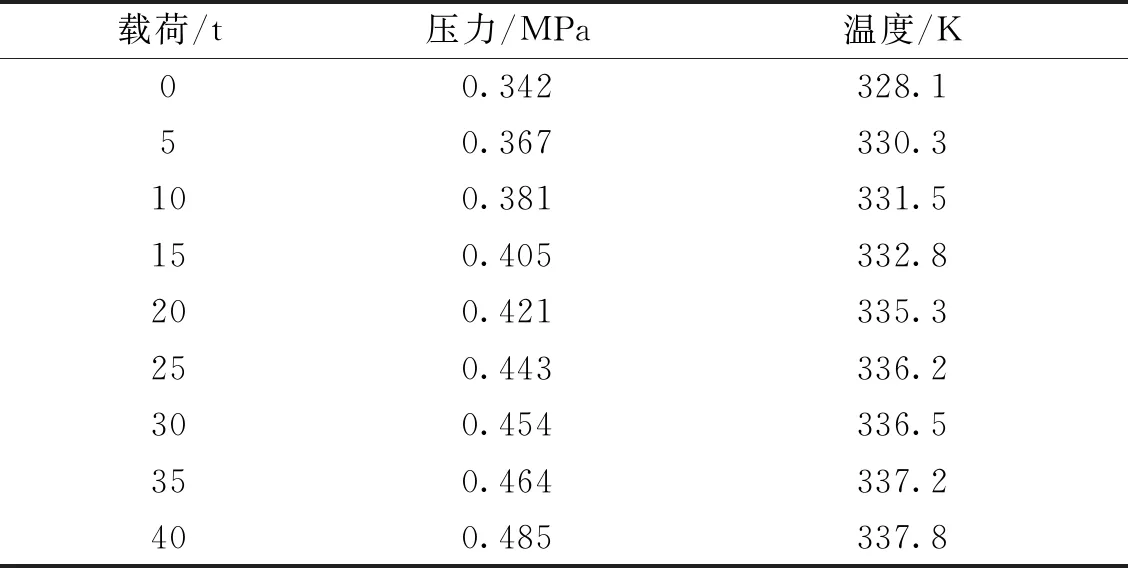
表2 旋转速度为135 r/min时不同承载的油膜压力场和温度场

由表3数据可知，旋转工作台处于极端载荷时，转速在135 r/min之内，随转速增加油膜压力线性增加，转速超过135 r/min时，油膜压力增加变缓，而油膜温度始终保持线性增加。

4 转速与承载能力协同匹配实验

双矩形腔静压支承转速和承载能力的匹配关系实验在静动压性能实验台上进行，通过测试转速与承载大小实现。转台直径3 100 mm，自重19 t，电机额定功率75 kW，转速1 600 r/min。装置由液压站、电气控制装置、静动压支承工作台、交流变频调速电机和十二点等量分油器组成，如图9所示。为了验证极端工况时双矩形腔静压支承旋转速度和承载能力的匹配关系，体现PV值恒定理论。在一个油腔上安装了6个压力传感器，另一个油腔上安装了5个温度传感器。传感器安装如图10和图11所示，数据采集和显示系统如图12和图13所示。由于受实验加载载荷的限制，现场只有10 t和19 t载荷，所以对其承载10 t和19 t载荷时的旋转速度匹配关系进行了验证，实验数据如表4所示。

图9 转速与承载力匹配关系实验装置

图10 压力传感器安装位置

图11 温度传感器安装位置

图12 数据采集系统

图13 数据显示系统

表4 10 t和19 t载荷时旋转速度实验值

对比表1理论数据和表4实验数据可以发现，实验数据与理论计算结果一致性较好，在工作台转速为125 r/min时其承载为19 t，在工作台旋转速度为135 r/min时其承载降至10 t。随着承载重量增加油膜温升增大，工作台转速相应降低，与表2规律一致。随着转速增加油膜温升增大，承载能力逐渐下降，与表3规律一致。若继续加大承载重量或增加工作台转速，位移传感器报警，静压支承工作台自动停机，实验无法进行，即可确定转速和承载能力的协同匹配值。

5 结论

1)推导了极端工况下双矩形腔静压支承转速与承载能力协同匹配关系数学模型，并对微间隙油膜压力场和温度场的载荷和转速特性进行了数值模拟，搭建了转速与承载能力协同匹配关系实验台，验证了理论计算和数值模拟的正确性。

2)随转速增加油膜温度增大，承载能力逐渐下降，转速为125 r/min时其承载为19 t，转速为136 r/min时其承载降至10 t，呈非线性关系。随承载重量增加，油膜温度和油腔压力增大，其旋转速度相应降低，二者存在非线性关系，但具有确定合理匹配值，体现了PV值恒定。

3)转速与承载增大均增加间隙油膜剪切和挤压发热，导致油膜温度升高，间隙油膜厚度下降，若匹配不合理将出现边界润滑或干摩擦，严重时发生静压支承摩擦学失效现象。建议通过减少油腔摩擦面积、采用低粘度润滑油、适当加大油膜厚度等方法，增加高速重载极端工况静压支承的承载能力或提高旋转速度。