导弹发射装置刚柔耦合动力学仿真分析
姚建均, 王枭, 刘宁, 梅宇, 吴杨, 余歌扬
(1.哈尔滨工程大学 机电工程学院,黑龙江 哈尔滨 150001; 2.中兴通讯股份有限公司, 广东 深圳 518000)
导弹发射系统是现代反空袭作战武器的重要载体,而导弹发射装置的设计是一个复杂而耗时的工程,其结构设计和优化离不开发射动力学的研究。利用导弹发射动力学指导发射装置设计,不仅可以缩短发射系统的产品设计周期,还可以提高武器系统的产品性能[1]。虚拟样机仿真实验可以近似代替导弹的实际发射过程,在保证模型精确的前提下,为导弹发射装置的结构优化和发射性能提高提供依据,缩短了武器系统的研发过程,降低了实验难度,缩减了生产成本[2-3]。
崔龙飞[4]利用刚柔耦合理论建立了车载武器动力学模型,将地面-发射车-发射炮作为一个整体,研究了速度和路况对车载武器发射振动的影响。乔禹[5]利用多体系统传递矩阵法构建了车载武器的动力学模型。赵岩[6]利用虚拟样机技术,研究了火箭转载时的动态响应。丰佩[7]将车架、发射箱等转变为柔性体,分析了起竖和发射过程的场坪的动态变化。武秋生[8]利用哈密顿原理和模态离散方法,建立了航天器离散形式的刚柔耦合动力学仿真模型,对航天器姿态运动和协同控制进行了研究。Low等[9]提出了Lagrange方程,并根据Hamiton原理建立多柔体动力学体系。
在多体系统动力学研究方面,FIJANY等[10]在分析结构的拓扑时,利用低序体阵列和矩阵变换,推导出了Kane-Huston方法。刘颖等[11]提出基于计算多体系统动力学的机织物卡尔丹角多体动力学模型。张乐等[12]将向后差分法引入双循环隐式积分法中,构造一种新的双循环隐式积分求解方法。张惠民等[13]讨论了不同隐式求解法在不同情况下的应用优势。
丁娟[14]基于变结构多体系统动力学的建模理论,描述了火箭发射系统中所遇到的几类变结构问题,建立了变结构火箭发射系统的动力学方程。姚瑞华[15]基于节点坐标的浮动坐标系,推导了柔性机械臂系统的刚-柔耦合动力学方程。张威[16]采用自然坐标法和绝对节点坐标法,构建了航天器太阳电池阵多体系统的刚-柔耦合动力学模型,研究了航天器位置偏移和姿态扰动的规律。
基于多刚体系统的发展,Wittenburg[17]首次在动力学专著中提出将图论法运用到多刚体系统分析中。孙棕檀[18]对多柔性体任意节点之间采用相似变换和铰变换的方法进行求解,建立了多体系统的刚柔耦合模型,从整体层面对柔性体进行分析。Eberhard等[19]结合了Krylov子空间方法和传统的Gramian矩阵降阶法,缩减了模型规模,降低了系统的计算难度。彭慧莲等[20]基于物理样机实验数据,利用深度学习方法,获得了较为准确的间隙铰模型。
但是在导弹发射系统的仿真分析中,还并未有基于多体系统及刚柔耦合系统原理的初始扰动因素影响分析。本文在以上的研究背景下,利用发射动力学和刚柔耦合理论,分析导弹发射装置工作原理,并建立多刚体动力学和刚柔耦合动力学模型,进行导弹发射的动力学研究。分析导弹发射时关键位置的振动响应,并对引起初始扰动的因素进行仿真分析。
1 多体系统动力学模型
1.1 导弹发射车结构
导弹发射装置模型主要由发射车、回转平台、发射架、平衡机构、方向机、发射箱、导弹等部分组成,其整体结构如图1所示。

图1 导弹发射装置整体结构
回转平台主要安装在发射车回转支撑上,通过位于回转平台上的方向机输出齿轮与回转座圈连接,发射架由本体钢架结构、左右耳轴座、前后导轨、前后锁紧机构、转接板固定销、基准平台等焊接成型,电动高低机通过销连接固定到回转平台下舱和发射架耳轴上。平衡机构由支座、扭杆弹簧、转臂、连杆等构件组成。
1.2 导弹发射车拓扑结构
根据导弹发射装置的结构特点及运动特性,可将发射装置划分为:车体部分、回转部分、起落部分、发射部分。根据“体”、“铰”编号原则,导弹发射装置的车轮、发射装置的回转平台均被视为刚性体,发射架起落部分被视为弹性体,车轮与地面之间的连接、车轮与车体之间的连接被视为弹簧连接,回转平台与发射装置车体及起落装置之间的连接被视为空间弹簧和扭簧,6个发射箱和上下转接板及定向管被视为固连刚体,可得到如图2所示的发射装置拓扑结构图。

图2 导弹发射装置拓扑结构
1.3 传递方程
1.3.1 弹簧及扭簧传递方程
导弹发射装置拓扑结构图2中,铰1-1、…、铰1-8、铰2-1、…、铰2-8、铰3、铰4、铰5-i、铰6-i(i=1,2,3,4,5,6)为连接“体”与“体”之间的空间弹簧和扭簧,其传递方程为:
Zr,O=UrZr,I
式中:r为1-1、1-2、…、1-8,2-1、…、2-8、3、4、5-i、6-i;Zr,I和Zr,O分别表示元件的输入状态矢量和输出状态矢量;Ur为传递矩阵。
1.3.2 振动缸体传递方程
刚性元件体1-1、体1-2、…、体1-8、体2、体5-i、体6-i、体7-i(i=1,2,3,4,5,6)为空间中一端输入一端输出振动刚体,传递方程为:
Zr,O=UrZr,I
式中:r为1-1、1-2、…、1-8、2、5-i、6-i、7-i。
元件4为1端输入2端输出的刚体,传递方程为:
式中H为变换矩阵。
车体2为8个输入端1个输出端的振动刚体,其传递方程为:
1.3.3 弹性梁传递方程
体4为发射架起落部分,本文中作为弹性体处理,同时考虑了弹性体4的横向、纵向、扭转方向的振动,其传递方程为:
Zr,O=UrZr,I(r=3,4)
1.3.4 方向角与射角变换方程
当方向角为α时,状态矢量Z2,3位于以体2和铰3的连接点为坐标原点,以导弹发射方向在水平面上投影为正向的坐标系i2XYZ上。状态矢量Z2′,3位于以输入端i2(2,铰3)为坐标原点,以车体向前为正的坐标系i2X′Y′Z′上。2个坐标系之间的相差角度为方向角α,须经坐标变换:
Z2,3=HαZ2′,3
1.3.5 总传递方程
由上述元件传递方程可推导出,从地面到导弹发射装置定向管的总传递方程为:
UallZall=0
式中:Uall为总传递矩阵;Zall为各边界状态的状态矢量。
1.4 刚柔耦合动力学方程
运用拉格朗日乘子法,得到任意柔性体或刚性体的动力学方程为:
(1)
式中:T为任意柔性体或刚性体的动能;QT为广义力,分为外部激励Qe和弹性变形Qv;C为阻尼;qj为第j个体的广义坐标。对式(1)进行推导可得:
式中:ξ为阻尼;n为多体系统中柔性体和刚性体的个数总和。
以C(q,t)=0表示系统的约束方程,则机械系统的刚柔耦合动力学方程为:
2 动力学仿真分析
2.1 发射装置动力学仿真分析
基于多刚体模型,建立导弹发射装置的刚柔耦合模型。本文将发射装置的刚性发射架替换成柔性体,建立导弹发射装置的刚柔耦合模型。
为保证在机械系统动力学自动分析(automatic dynamic analysis of mechanical systems,ADAMS)搭建发射装置虚拟样机模型的可靠性,定义以下约束:发射车底座与回转台间的扭转弹簧阻尼器、回转平台耳轴和转臂连接处对称的扭转弹簧阻尼器、低机伸出轴与回转电机之间的拉压弹簧阻尼器、导弹和发射箱之间的碰撞接触。同时,将导弹发射时可能受到的外部激励因素,如导弹自重、重心移动导致的惯性力、发动机推力、闭锁挡弹器的闭锁力、燃气流作用力等添加至仿真模型当中。
2.1.1 导弹运动参数分析
以导弹质心为测量对象,分别测得多刚体系统和刚柔耦合系统在发射过程中的导弹速度和加速度,测量结果如图3所示。
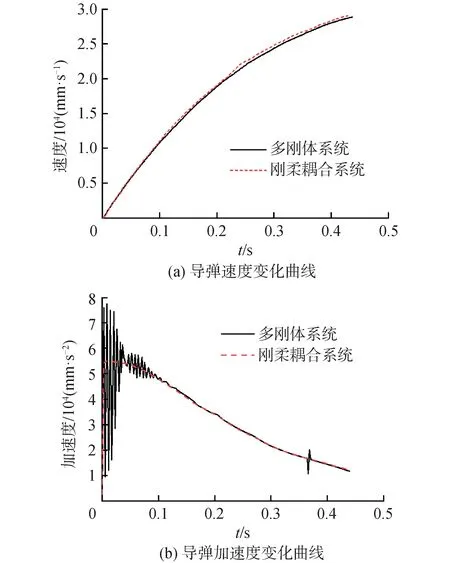
图3 导弹速度与加速度曲线
由对比图3可知,对于刚柔耦合系统,导弹加速度变化趋势与多刚体系统一致,但是由于柔性体结构自身具有吸收振动冲击的作用,导弹加速度变化较为平缓,没有太大的波动。
2.1.2 导弹出箱姿态分析
在图4所示的弹轴坐标系的基础上,对导弹出箱姿态进行定义。导弹在俯仰方向、偏航方向的角速度变化情况分别如图5所示。

图4 导弹姿态角示意

图5 导弹角速度曲线
对比刚柔耦合系统和多刚体系统在俯仰姿态和偏航姿态的角速度变化可知,刚柔耦合系统在角速度变化上更加平缓,峰值波动较小,而刚体系统角速度峰值较大,振动强烈。
2.1.3 发射架振动分析
导弹发射装置的俯仰角度为30°时,对多刚体系统和刚柔耦合系统进行动力学仿真,分别对发射架下转接板上的节点进行测量,俯仰方向和偏航方向的角速度和线速度变化曲线如图6所示。
由图6可知,由于柔性体自身具有吸收振动的作用,在受到冲击时,会发生连续蠕变,吸收振动,因此刚柔耦合系统的角速度、线速度变化较小。

图6 发射架速度与角速度曲线
2.2 初始扰动因素影响分析
2.2.1 发射间隔影响
分别对发射间隔为0.3 s、0.6 s、1.0 s的2发导弹进行动力学仿真,其俯仰和偏航方位的角位移和角速度曲线如图7、8所示。
分析图7、8可知,增加2发导弹之间的发射间隔,可以使第2发导弹发射时系统的振动减小。由图8(b)和图8(c)可知,在第1发导弹发射0.5 s后,定向器在俯仰和偏航方向的角位移和角速度减少为最大幅值的10%,在大约0.7 s左右,角速度和角位移接近于零,此时,第1发导弹产生的燃气流冲击力被系统阻尼和柔性体吸收。
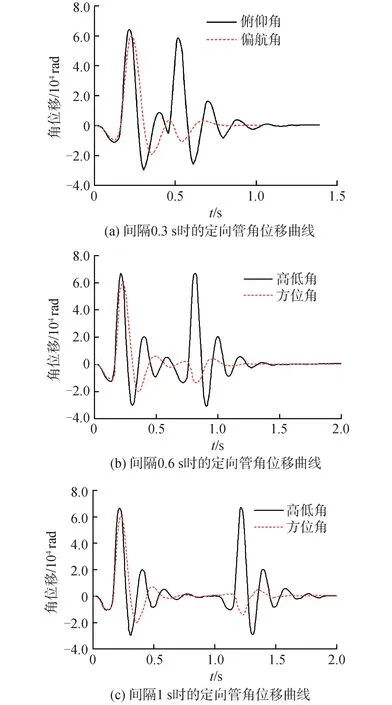
图7 不同间隔定向管角位移曲线
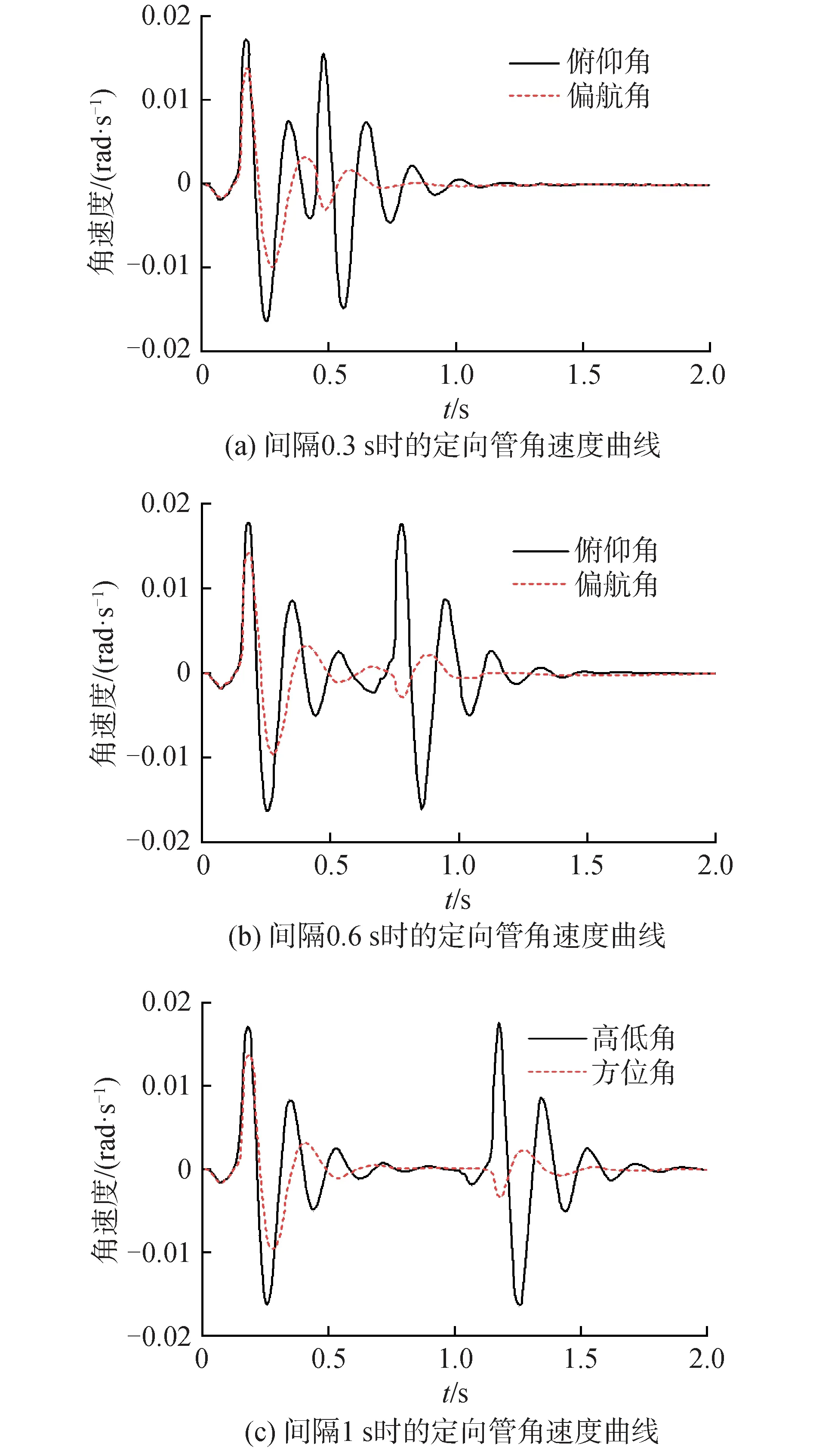
图8 不同间隔定向管角速度曲线
对第2发导弹刚开始发射时的定向器运动参数进行统计,如表1所示。其中θp、ωp、θY、ωY分别表示第2发导弹在不同发射间隔情况下,发射箱定向器在俯仰和偏航方向的角位移和角速度;ωM1、ωM2分别表示第2发导弹发射结束,第3发导弹开始时,定向管在俯仰方位和偏航方位的角速度。

表1 定向器运动姿态参数描述
由表1分析可知,发射间隔分别为0.3 s、0.6 s、1.0 s时,定向器在俯仰和偏航方向的角位移和角速度随着发射间隔的增大逐渐减小。因此,在导弹发射时,可适当增加2次发射间隔,使燃气流冲击衰减到一定程度再发射下一发导弹,以减少发射系统的振动冲击。
2.2.2 燃气流影响
燃气流对发射系统的扰动主要表现为3个方面:燃气流冲击力、反溅流干扰、二次流干扰,本文主要分析燃气流的影响。在ADAMS中进行动力学仿真时,首先对某一位置的导弹施加燃气流力,分析燃气流作用下导弹在俯仰方向和偏航方向的运动特性,然后在相同条件下,通过传感器作用使燃气流冲击力失效,同样测得导弹在俯仰方向和偏航方向的运动特性。图9为导弹俯仰方向姿态变化的仿真结果,图10为导弹偏航方向姿态变化的仿真结果。

图9 导弹角速度与角加速度曲线
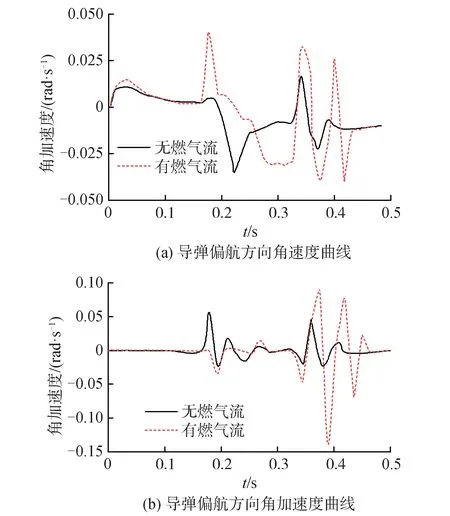
图10 导弹偏航方向角速度与角加速度曲线
仿真结果表明,燃气流是影响导弹发射精度的主要因素。由于导弹发射时,在俯仰方向上会受到反溅流作用,并且燃气流会放大导轨不平直的影响,所以有燃气流的仿真结果中俯仰方向比偏航方向冲击更剧烈。即不考虑燃气流的仿真模型无法真实地反映导弹发射过程的初始扰动。
2.2.3 闭锁力影响
在研究闭锁力大小对初始扰动影响的动态仿真时,设置静平衡的时间为1.0 s,对闭锁力大小分别设置为2、5、8 kN,研究导弹发射装置动态响应情况。施加不同大小的闭锁力,导弹在定向器内的发射速度曲线如图11所示。
对图11的数据进行分析,3种不同闭锁力下,导弹初始运动时刻、出箱时刻、在发射箱内的运动时间、导弹出箱速度如表2所示。

表2 导弹发射过程动态参数
根据表2可知,导弹的速度随着闭锁挡弹器闭锁力的增大而增大,导弹在发射箱内的运动时间随闭锁力的增大而减少。这是因为闭锁力越大,闭锁挡弹器解除锁定时间越长,施加到导弹上的导弹推力和燃气流力的合力越大,会使导弹加速度越大,出箱口时的速度越大,运动时间越短。导弹出箱口速度越大,发射散布度越小,发射精度越高。
在不同的闭锁力下,导弹在俯仰方向和偏航方向上的角位移变化曲线如图12所示。由图12可知,导弹在解除闭锁挡弹器锁定约束后,俯仰方向和偏航方向有较大的角位移变化,表明存在闭锁力引起的初始扰动。随着闭锁力的逐渐增大,导弹的角位移随之增大,导弹发射装置振动更强烈,初始扰动也随之增大。由于闭锁力是一个单位阶跃函数,在进行实际发射过程中,会增加导弹的初始扰动,所以选择闭锁挡弹器的闭锁力时,在满足导弹初始时刻不发生位移的情况下,应尽可能选择较小的闭锁力。
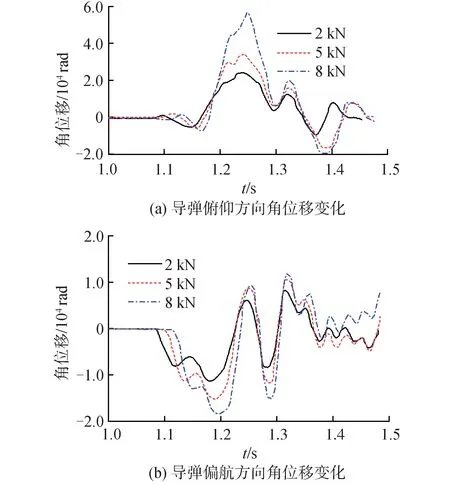
图12 导弹角位移曲线
3 结论
1)多体系统传递矩阵法和刚柔耦合理论,有利于搭建导弹发射系统的动力学传递方程,构建刚柔耦合分析模型,研究不同因素对导弹的发射状态的影响,在导弹发射系统的研究中具有重要意义。
2)多刚体系统和刚柔耦合系统2种模型的导弹出箱速度近似,但多刚体系统在0.1 s前振动剧烈,而刚柔耦合系统加速度较平缓,多刚体系统的加速度幅值是刚柔耦合系统的1.45倍。在发射架的俯仰和偏航方向,刚柔耦合系统也能快速吸收振动。
3)发射间隔越大,初始扰动越小;燃气流冲击对俯仰方向的角速度影响较大,对偏航方向影响较小;随着闭锁挡弹器闭锁力的增大,导弹的速度和角位移有明显的增大,同时,导弹发射装置有较大的振动,初始扰动也随之增大。
本文基于理论推导和仿真计算,研究了导弹发射车动力学系统。理论仿真和实验的对比研究,有待进一步的探讨。

