部分定体积几何体的表面积极值讨论部分定体积几何体的表面积极值讨论

◎王丽萍 张万龙

(首钢工学院基础学院，北京 100144)

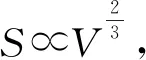
本讨论中用到了极值思想.极值问题是经典微积分学中最成功的应用，无论在科学研究，还是在实际工程中、运筹规划方面，将问题转化为求解某种极值是十分常见的.

一、定体积圆台表面积极值

再将上述表达式代入表面积公式S中，得到表面积表达式为

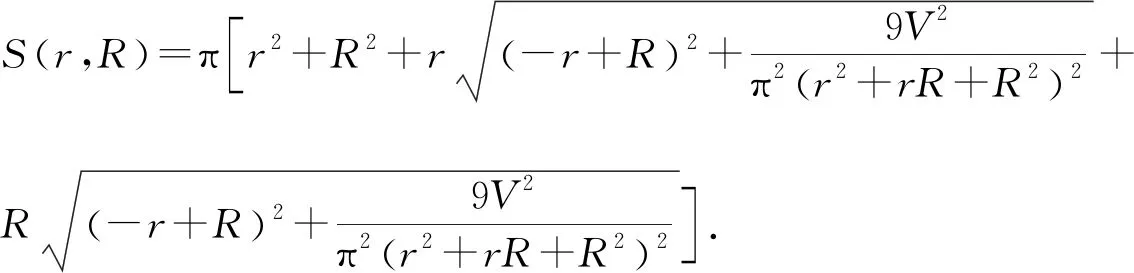
(1)

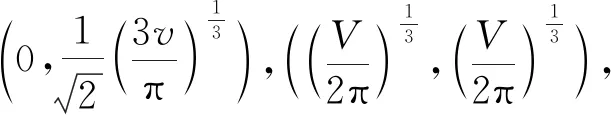
(2)

又因为圆锥的表面积为

S=πR2+πRl.

(3)

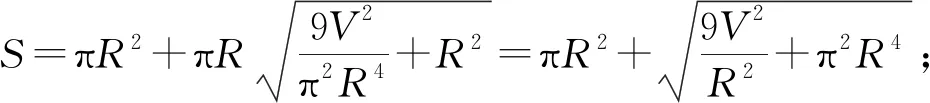
(4)

将(4)式两边平方，然后化简得:

2Sx2-S2x+9V2π=0,

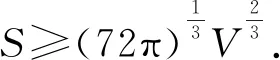
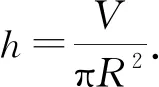
S=2πR2+2πRh

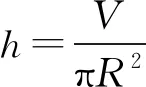
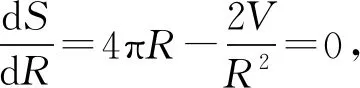
二、定体积球缺表面积极值

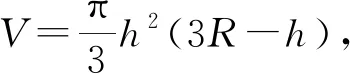
S=π(2Rh+R2-(R-h)2)=π(4Rh-h2).

(5)

(6)

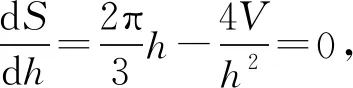
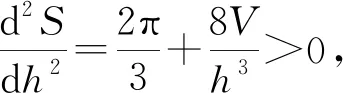
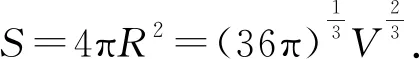
三、定体积长方体表面积极值

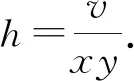
(7)

下面通过两种方法求其表面积公式(7)的极值.

(一)初等方法

即

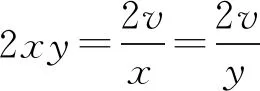
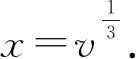
因此，当长方体的表面积取得最小值时，正是同体积下正方体的表面积.

(二)极值法

分别对(7)式中的x,y求偏导得下面的偏导公式：

(8)

(9)

令(8)(9)两式为0，得到以下偏导方程组：

(10)

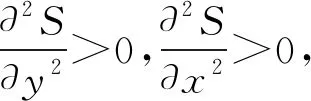
四、定体积锥球结合体的最小表面积

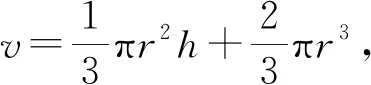
(11)

通过计算组合体的表面积，得到表面积公式为：

s=πrl+2πr2.

(12)

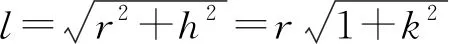
将斜高公式代入组合体的表面积公式，得

(13)

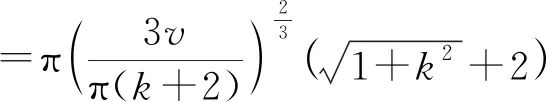
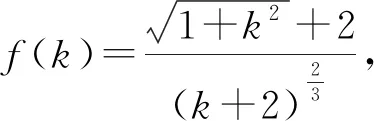
对f(k)求导可得到

化简可得到

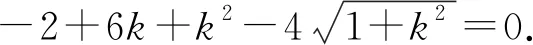
五、结束语

通过对定体积圆台、球缺、长方体表面积极值的讨论，我们可以发现：定体积圆台取得最大表面积时为圆锥，取得最小表面积时为圆柱；定体积球缺取得最小表面积时为球体；定体积长方体取得最小表面积时为正方体.本文通过比较几何体表面积的极值，发现了36π<54π<216<72π，因此对于体积一定的几何体，最小表面积从小到大的排列顺序为球体、圆柱体、正方体、圆锥体，同时，也能得到体积相等的立体图形，越接近球，表面积越小的结论.