渔舟唱晚波浪函数，数形结合落实素养渔舟唱晚波浪函数，数形结合落实素养——函数y=Asin(ωx+φ)教学设计与思考

◎魏清泉 张肇勋

(1.山东省青岛市教育科学研究院,266011;山东省青岛市即墨区第一中学，266200)

一、教学分析

在自然界、生活和生产实际及科学技术中，周期现象俯拾皆是.在本章我们以单位圆上的匀速圆周运动引入函数y=sinx，y=cosx.这两个函数是刻画周期变化现象的基本数学模型，它们是“标准化”的结果.将单位圆上的运动进行扩展，就到了本节的“一般的匀速圆周运动”，其扩充点有圆的半径、起点位置、角速度等，而刻画这些现象的数学模型就是函数y=Asin(ωx+φ).对于这部分内容，以往教科书往往侧重研究“图像变换”，即参数A，ω,φ对函数y=Asin(ωx+φ)图像的影响,从而使得教师在教学中把注意力集中在三角函数图像的平移和伸缩变换上，让学生形式化地记住“左加右减，上加下减”等口诀，而对这个函数的实际意义却不加关注.新课标的背景下，数学教学应着眼于开放，注重唤醒学生的开放意识与创新思维.所以，结合新版本的教材，笔者将从研究筒车运动开始，构建周期变化的函数模型，经过数学建模，获得函数y=Asin(ωx+φ)，明确函数模型中参数的实际意义，再通过对该函数模型的研究获得其图像与性质等相关结论.

二、教学实录

上课开始和学生一起欣赏一首曲子《渔舟唱晚》，用音乐软件的视觉效果波浪线向学生展示声音的变化，定格一个画面.

老师：大家想一下，在欣赏音乐的过程中，大家看到的如屏幕展示的跳动变化的曲线是什么呢？

学生：声音的波动图.

老师：没错！看到这个图像大家能联想到我们数学上学到的什么相关知识？

学生：三角函数图像.

老师：大家的数学感知能力是非常准确的，其实音乐中的每一个音的声波都是一个三角函数，就像我们屏幕上展示出来的这三个三角函数图像，每个图像都代表一个音(用几何画板展示)，而平时我们听到的音乐是由许多个音节合成的复合音，把每个音对应的函数合在一起，就成了现在所展示的声波曲线(几何画板展示)，这跟我们刚才看到的音乐波形图是非常相像的.所以说，数学来源于生活，只要我们带着数学的眼光善于发现问题，就能感受到数学无处不在.现在我就有这样一个问题：刚才展示的三个音的图像都是三角函数图像，但是图像却是不同的，图像的不同是由什么影响的呢？这就是我们这节课要探究的问题.首先看一下本节课的学习目标：(课件出示学习目标，给学生留时间阅览)

老师：要解决上面提出的问题，我们需要结合实际情境，建立一个适合解决问题的数学模型，这个实际问题与匀速圆周运动有关，比如筒车的运动.大家先一起看一个视频，体会筒车的工作原理(播放视频).

老师：从视频中我们可以看到筒车的工作原理：假设水流量稳定，筒车上的每一个盛水筒都可以看成一个质点，它们在周而复始地做匀速圆周运动.关于筒车这个实际运动情景，相信大家可以提出很多与数学相关的问题.我们今天主要来研究一下盛水筒在匀速圆周运动的过程中相对水面高度有关的问题.为了方便研究，我们把筒车抽象成如图所示的几何图形.在水流量稳定的情况下，筒车从P0处出发，逆时针做匀速圆周运动到达P点的过程中，盛水筒距离水面的相对高度H都与哪些量有关？尝试用数学符号去表示这些量.

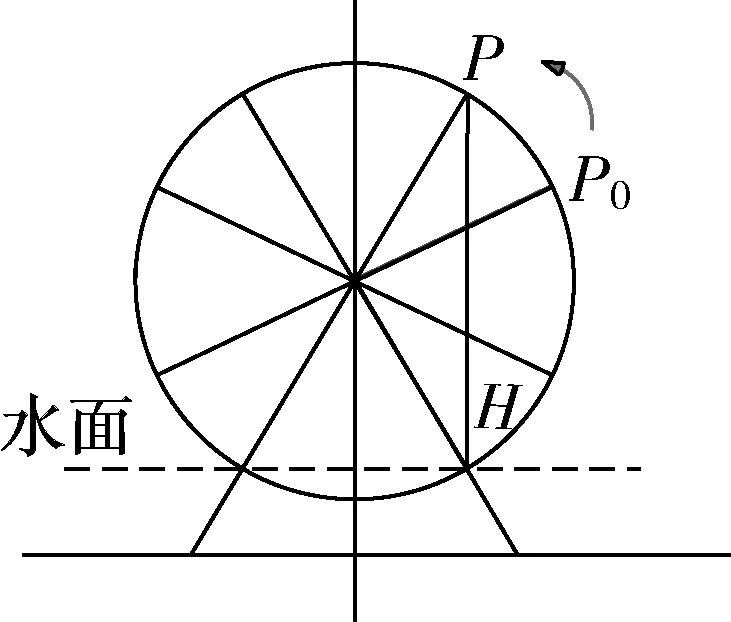
图1

学生：筒车的半径r、筒车转动的角速度ω、转轮中心到水面的距离h

老师：还有没有补充？

学生：还跟转动经过的时间t有关系.

老师：大家找得非常准确，我们先把各个量标记到图像上(课件展示)，大家接着考虑与高度H有关的这些量中谁是常量？谁是变量？

学生：筒车的半径r、筒车转动的角速度ω、转轮中心到水面的距离h是常量，转动经过的时间t为变量.

老师：那大家想一下，盛水筒相对水面的高度H与转动经过的时间t是否成函数关系？为什么？

学生：成函数关系，因为每一个时间t都有唯一确定的高度H与之对应.

老师：大家解释得非常准确，既然两个变量之间成函数关系，那么结合筒车的运动特点，你将选择一个怎样的函数模型来刻画盛水筒相对水面的高度H与时间t的关系呢？

学生：三角函数，因为筒车周而复始做匀速圆周运动，具有周期性.

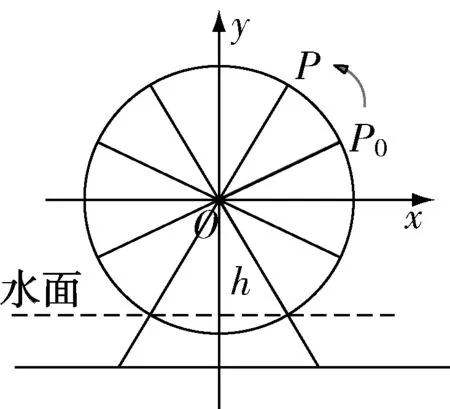
图2

老师：很好，大家对于三角函数的特点理解得非常到位.我们要通过函数解析式解决问题，按照已有的做题经验，最好能建立一个坐标系，如何建系更加合适？

学生：以水车轴心O为原点，以过O点平行于水面的直线为x轴，过O点垂直于水面的直线为y轴建立坐标系.

老师：回答得非常严谨，大家鼓励一下(掌声).在该坐标系的基础上，当t=0时，盛水筒M从初始位置P0，以ω(rad/s)角速度，经过t(s)，逆时针运动到P点，其中以Ox为始边，以OP0为终边的角为φ，请大家思考转动过程中盛水筒相对水面的高度H与时间t的函数模型具体是什么？

学生通过思考探究后，举手展示自己得到的结果.

学生：我得到的函数关系式为：H=rsin(ωt+φ)+h.

老师：解释一下，你是怎么得到这个结果的？

学生：水筒到水面的相对高度可以看成水筒到x轴的距离与轴心到水面的距离的和，其中转动过程中水筒OP与x轴的夹角为ωt+φ，所以水筒到x轴的距离为rsin (ωt+φ)，这样就得到了H与t的关系式.

老师：大家有不同的答案吗？(没有别的意见)这位同学分析得非常有条理，表述很准确，掌声鼓励一下(掌声).板书探究得到的函数关系式：H=rsin (ωt+φ)+h.

老师：这里的h是常量，我们暂且不做研究，关系式中剩余的t是自变量，H是因变量，我们习惯上用x，y来表示自变量和因变量，所以我们可以把该函数模型写成这样的形式：H=Asin (ωt+φ)+h，这个函数模型就是用来刻画筒车这样的质点做匀速圆周运动的，其中每个量的意义是什么呢？

学生：A是半径，ω是角速度，x是转动的时间，φ是起始位置与x轴的夹角，H就是对应的高度.

老师：大家理解得不错，我们看到这个函数，很容易想到之前学过的正弦函数y=sinx，这两个函数在参数的取值上有什么关系呢？

学生：函数y=sinx中A=1，ω=1，φ=0.

老师：结合我们对参数意义的理解，这也正印证了正弦函数刻画的就是质点在单位圆上，以单位速度，从A(1,0)点出发做匀速圆周运动.我们知道函数y=Asin (ωx+φ)的图像由参数A,ω,φ所确定，只要我们弄明白这三个参数的变化对图像的影响，就能把握这个函数的性质了.下面，我们利用刚才建立的数学模型，结合对函数中每个量意义的理解，借助筒车有关的几个实际问题，探究参数ω，φ对三角函数图像变化的影响.

应用探究1:现在有一半径为1 m的筒车，共均匀安装了12个水筒，在雨季筒车的转速为1 rad/s，则相邻的两个水筒相继到达最高点的时间差是多少？

学生思考后，举手展示结果.

三、教学感悟

本节内容为高中数学人教A版5.6章节“函数y=Asin(ωx+φ)”.在自然界、生活和生产实际及科学技术中，周期现象俯拾皆是.在本章5.2.1这一节，我们以单位圆上的匀速圆周运动引入函数y=sinx，y=cosx.在5.4.1这一节我们又结合点在单位圆上的匀速圆周运动特点，在三角函数定义的基础上，继续学习了y=sinx，y=cosx的函数图像.这两个函数是刻画周期变化现象的基本数学模型，它们是“标准化”的结果.研究它们的图像与性质可以为研究其他周期变化现象奠定基础.将单位圆上的运动进行扩展，就到了本节的“一般的匀速圆周运动”，其扩充点有圆的半径、起点位置、角速度等，而刻画这些现象的数学模型就是函数y=Asin(ωx+φ).对于本节内容，教材定位于构建周期变化的函数模型，从研究筒车运动开始，经过数学建模，获得函数y=Asin(ωx+φ)，从而明确函数模型中参数的实际意义，再通过对该函数模型的研究获得其图像与性质等相关结论.对于这部分内容，以往教材往往侧重研究参数对函数y=Asin(ωx+φ)图像的影响，因此教师在教学中一般把注意力集中在三角函数图像的平移和伸缩变换上，让学生形式化地记住“左加右减，上加下减”等口诀，对这个函数的实际意义却不加关注.而新版教材在本节首先提出研究任意匀速圆周运动如何用数学模型刻画的问题，通过筒车这一生活实际，在理解函数模型实际意义的基础上，研究参数对函数图像的影响，注重以学生为本，能够让学生更好地体会研究函数的一般思想和方法.我们在整个教学过程中始终贯穿了由简单到复杂、由特殊到一般的化归思想，同时还力图向学生展示观察、归纳、类比、联想等数学思想方法。通过本节课的学习，学生能够将已有的知识形成体系，从而为进一步探索研究其他数学问题奠定基础。下面笔者将从三个方面对本次课程进行反思评价。

(一)自我评价——用模型、探究的观点设计复习课

本节课笔者通过学生熟悉的物理实际问题引入课题，为新课的学习创设情境，拉近了数学与现实的距离，激发了学生的求知欲。同时，让学生结合筒车模型经历刻画匀速圆周运动的数学建模过程，旨在培养学生的数学建模素养.其中，构建的函数模型转化为一般函数形式y=Asin(ωx+φ)涉及了三个参数A,ω,φ，在教学过程中，考虑到课时时长，笔者只设计了ω，φ这两个参数对三角函数图像变换的影响.为了降低学生学习的难度，笔者设计了三个探究问题，分别从三个方面来研究函数图像的变换：

(1)探究参数φ对函数y=sin(x+φ)的图像有怎样的影响.

(2)探究参数ω对函数y=sin(ωx+φ)的图像有怎样的影响.

(3)探究函数y=sinωx的图像如何变换为y=sin(ωx+φ)图像.

在教学过程中，笔者一直以这个探究为主线，每个探究环节都结合筒车的匀速圆周运动设置了实际情境和探究问题串，以问题引领学生探究，借助实际情境帮助学生理解探究结果,并且运用几何画板软件画出函数的图像，更加直观地分析了两个参数对函数图像的影响，且对学生的探究结论给出验证。这样的处理有效降低了学生接受新知识的难度，所以学生在第三个探究中才能比较自然地将前两个探究综合起来，从而得到第三个探究的结论，而这既是本节课的重点，也是本节课的难点.

(二)问题反思——用联系变化的观点设计问题

本节课的教学思路是很清晰的，但是在具体操作过程中却是“仁者见仁，智者见智”.笔者对第二个探究的处理是有些缺憾的，缺憾在于几何画板的局限性导致了无法将每个点的坐标展示出来，不利于学生观察变换的特点.

(三)课堂重建——用实践的观点进行课堂重构

针对上面提出的缺憾，笔者对这节课做出如下调整：在上课时间允许的情况下，可以让学生先自己画出三个探究中每个函数的图像，然后再由老师用几何画板展示.加入这个环节，学生探究起来会显得轻松很多.因为学生自己在作图的过程中每个点都要标出坐标，可以弥补几何画板无法展示点的坐标的缺憾.

没有学习者体验、感悟的教学是无效的教学.培育学生核心素养即为学生创造美妙的学习体验，让学生通过主动思考、分析、展示、体验、创造获取数学知识，进而内化升华为数学能力，真正实现个性发展、终身发展.