感悟基本图形，提升初中学生数学解题能力感悟基本图形，提升初中学生数学解题能力

◎王 宁

(上海市嘉定区苏民学校，上海 201802)

随着基础教育新课程改革的不断发展，初中数学的教学方法和模式也在不断创新，这在很大程度上丰富了学生的数学思维.几何是数学的重要课程，其中含有大量以基本图形为构架的复杂图形，如果学生的空间想象能力不足，将会很难求解.基本图形指的是能够反映出某个定理和数学规律的图形.让学生自主感悟基本图形，可以让他们的思维处在最近发展区内，利于他们找到解决几何问题的思路.本文首先对基本图形的概念进行论述，然后对应用基本图形提升学生解题能力的意义进行说明，最后提出借助基本图形，提升初中学生数学解题能力的策略，希望对初中数学几何教学带来帮助.

一、基本图形概念

为了找到解决几何问题的方法，我们往往需要构建一个最简单、最重要、最基本的几何图形，该图形具有特定的性质，能够将题干中隐含的几何概念、公式等表现出来，我们将这样的图形叫作基本图形.初中几何中的基本图形数量并不多，但是这些图形却能将复杂的几何问题通过基本图形特有的性质变得简单化.这些基本图形包括：平行线、等腰三角形、全等三角形、与圆有关的角、相似三角形、特殊角三角形、与面积相关的三角形等.在应用基本图形进行解题的过程中，我们要根据问题中出现的已知条件找到题目中含有的基本图形，将不完整的基本图形补充完整，剖析每个几何问题的思维过程，从而提高解题的灵活性.

二、应用基本图形提升学生解题能力的意义

(一)可以起到语言转换作用

我们知道，学生在解题的时候因为读不懂题目意思而导致出错的概率很大.这说明学生对数学语言的理解还不到位，因此，培养学生的数学语言转换技巧对提高他们的解题能力大有裨益.而在培养数学语言转换能力时，学生可以通过画基本图形的方式来寻找解题的突破口.比如“平行线”是初中数学的重要知识点，平行线分线段成比例又是平行线的重要定理，其数学语言描述为：平行于三角形一边的直线，与它的两条边所截得的线段成比例.这个时候教师可以让学生根据定理的语言，自己画出基本图形，并对线段是否成比例进行验证.学生在理解定理的过程中，就能画出如图1所示的基本图形，这对于发展学生的信息挖掘能力很重要.

图1

(二)可以很好地规范学生的几何解题步骤

解决初中数学几何问题需要掌握一定的技巧，要做到“三看清”：看清题目中所讲的内容，看清楚题设的条件，看清要解决的问题.只有明确这三个方面，才能提高解题效率.借助基本图形，学生就可以根据基本图形的独有特性来归纳、发现并最终得到每一个几何问题的求解条件，将基本图形的性质应用到解题过程中，从而提升解题技巧，规范解题步骤.

三、感悟基本图形，提升初中学生数学解题能力的策略

(一)通过基本图形提炼加工其他图形

数学中的几何学主要是研究空间结构的一门学科，属于数学中最基本的研究内容.相关的教学经验表明，初中生已经具有很强的空间想象能力，之所以没有发挥出这种能力，主要是因为教师在让学生进行图形加工的时候未将基本图形的理念融入其中.因此，教师通过引导学生研究基本图形可以提高学生的基本解题能力.基本图形中隐藏着很多重要的几何知识，比如，在初中有关相似三角形的几何题中，经常会出现如图2所示的基本图形.该图形有一个重要的性质：∠C=∠ABD，根据该性质就会找到各边之间的关系为AB2=AD·AC.这个关系式非常重要，在很多相似三角形问题的求解中都能用到.教师可以引导学生对相似三角形的性质进行应用，从而提炼出其他的信息，这样，他们在进行更复杂的相似三角形相关问题的求解中，就可以以此图形为基本图形，将其当作“母图”，从而根据母图解题.学生在解题训练中找到的母图越基本，那么子图就会越丰富，学生在解决子图问题中就能够很好地应用各种数量关系.需要注意的是，基本图形的获得过程要让学生参与，基本图形不一定全是老师的总结和归纳，学生自己获得题目中的基本图形，这本身就是一个对知识点应用的过程，可以很好地培养他们的解题能力.

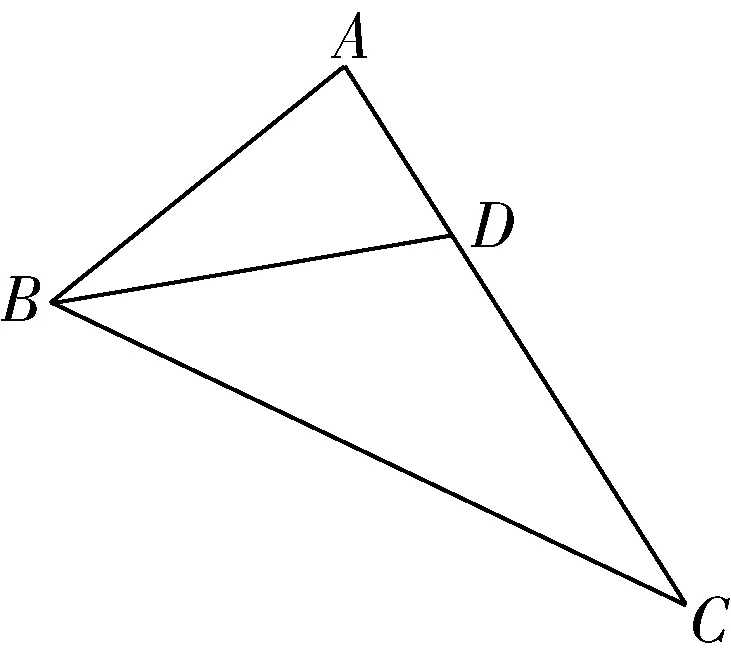
图2

(二)利用基本图形培养学生的解题思路

在利用基本图形提高学生解题思路的教学过程中，教师一定要树立学生的课堂主体地位，在解题的过程中要渗透数学思想和方法，提高学生的数学素养.同时教师要通过一题多解的方式促进学生思维的发展，让他们在解题的过程中能够融会贯通，并引导他们在解题后进行反思，以提高他们的综合解题能力.相关的教学实践发现，采用一定的策略去研究基本图形，会让学生更灵活地审题，将复杂和抽象的几何问题变得简单和具象化，起到事半功倍的效果.

比如，图3属于四边形中的一个基本图形，学生根据所学知识很容易得到各边的长度关系为：AP·BP=AD·BC.教师可以与学生一起对该四边形的性质进行概括：一线三垂直.这个性质属于该基本图形的基本性质，学生需要灵活掌握.学生在熟悉了该性质后，教师可以通过变式的方式向学生提供更深层次的习题，让学生学会应用.如将图3中的四边形ABCD转化为矩形，并沿着图形内的直线EF进行折叠，使点C正好落在边AB的中点上，将其记作C′，设点D的对应点为D′，两条直线C′D′与AD相交在M点，最终得到图4，请将AM的长用AB和BC表示出来.

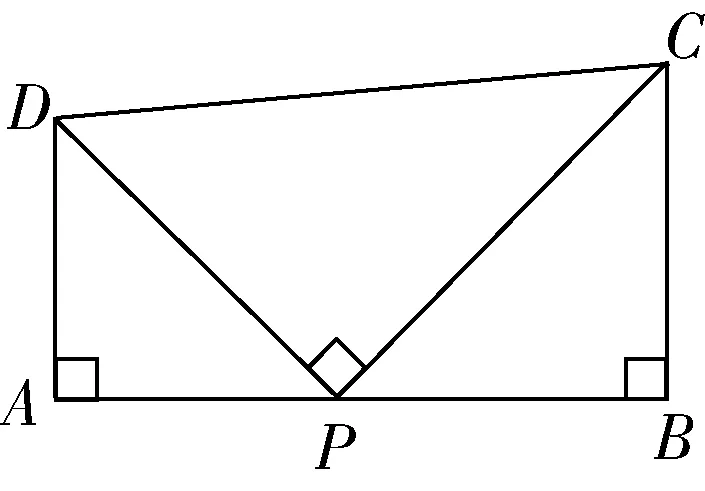
图3

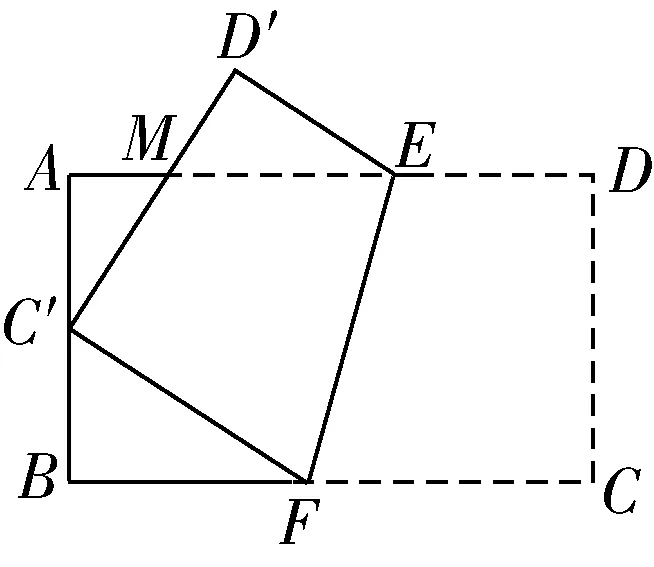
图4

对于几何中经常出现的折叠问题，学生通常会感觉难以下手，这与学生的空间想象力不足有关，他们无法对图形变换进行深入理解.基于此，对于该种基本图形变换题，教师要引导学生学会分析，让他们自己找到复杂图形中蕴含的“一线三垂直”特征.教学实践表明，学生有了上述的发现后，他们的解题思路将会非常明晰，会找到图4中的两个相似三角形，即△AC′M和△BFC′，这样后面的求解就变得很简单了.近些年中考中有很多开放性的综合题，其主要特点就是开放性、探究性和创新性，而这些综合题就是由一些基本图形改编而来的.在平时的训练中，教师要以基本图形为载体，对它们进行提炼、变式和拓展，训练学生的数学思维，以达到举一反三的目的.

(三)让学生学会“累加”，提高对基本图形的应用

基本的图形关系和性质是构建几何问题的基石，也是学生学好几何的关键.在实际的教学中，教师往往因为基本图形的简单而忽视让学生对图形进行应用.其实虽然原始基本图形简单，但是一些常见的基本图形经过简单的组合就能形成复杂的几何图形，其中蕴含着丰富的图形性质，形成了复杂的几何问题，这些问题会成为学生眼中的难题.在基本图形解题教学中，教师要从学生熟悉的平行线、等腰三角形开始，逐步逐级地让学生“累加”图形，慢慢地体会几何综合题是如何一步步形成的，这样可以增强学生对几何基础知识的巩固.“累加”图形教学可以这样进行：第一步，任意画出一个等腰三角形EAD，EA=ED，让学生快速说出其性质，即等边对等角、等角对等边，并告诉学生这是因为等腰三角形是最基本的轴对称图形.第二步，在上一步的基础上，让学生作出两个底边共线的等腰三角形：D是线段AB上的一点，以AD和BD分别为底边在AB的两侧作等腰三角形EAD和等腰三角形FBD，求证：AE∥BF.第三步：在第二步的基础上，过点F作AB的垂线，假如垂足为H，延长线AE和FH交于点C，求证：CE=FE.第四步：在上述步骤的基础上，连接CB,BE，如果恰好AB=BC，求证：EB=EF.第五步：在上述所有步骤的基础上，连接CB，如果AC边的中点为M，求证：DF=2EM.

通过上述五个步骤的图形“累加”后，最终得到了如图5所示的复杂图形.学生一步步地对图形进行变换，一边画图一边了解性质，就能求出各步骤中的证明题.通过五步训练，教师就把平行线、等腰三角形、直角三角形、平行四边形、三角形全等、线段的垂直平分线、中点等基础几何知识进行了有序的结合和应用，给学生揭示了各个基本图形之间的关系，让他们在解题过程中结合题干中给定的基本图形创建新的图形，从而提高解题能力.

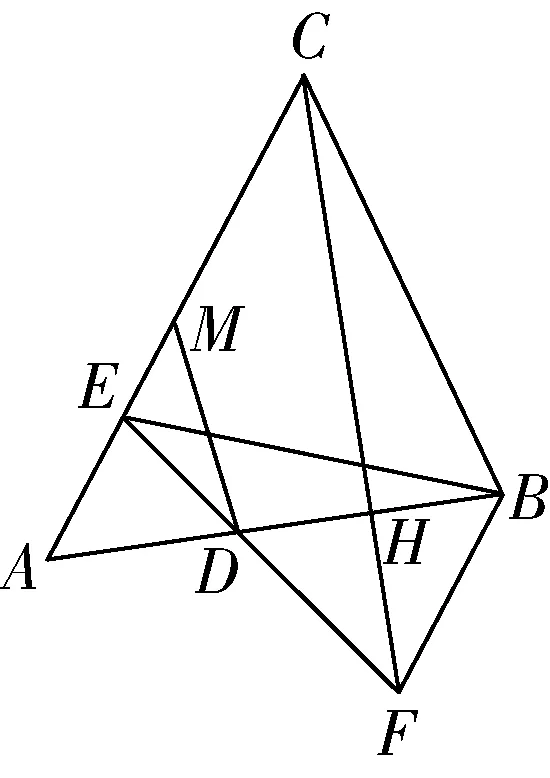
图5

(四)让学生在解题中学会“分割”，提高解题速度

在初中数学几何教学中，“分割法”是经常应用到的解题方法.通过分割的形式，可以让一些复杂的几何图形简单化，学生只需要将所学的知识进行迁移即可提高解题的速度.分割法的方式有很多，在实际的教学中，教师要带领学生读懂题意，引导他们从题干中挖掘出有价值的基本图形信息，进而应用到实际的解题中去.比如有如图6所示的一道数学题：将两个面积和周长相等的长方形重合在一起，求组合图形的面积.在解题的过程中，教师要让学生发挥空间想象力，思考如何将复杂的图形简单化.为此，可以将图形分割成两个全等的梯形，得到：S组=(7-2+7)×2÷2×2=24(平方厘米).在指导学生应用分割法的时候，教师要教给学生一些技巧，可以利用一些不规则图形的凹凸特点，将其分割成若干个可以计算的规则图形(如长方形、三角形、梯形等)，先将各个规则图形的面积计算出来，最后再把这些规则图形的面积加在一起，总面积就是不规则图形的面积了.为了提高学生的图形分割计算能力，教师要适当加大训练量，经常出示一些不规则图形让学生进行分割训练，并针对他们在分割中存在的问题进行纠正，从而提高他们利用所学知识解决数学几何问题的能力.

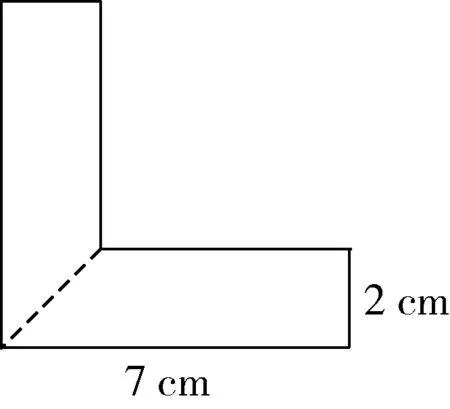
图6

(五)让学生在解题中学会“等量代换”，拓展数学思维

等量代换是一种非常有助于培养学生数学思维的数学教学方法，指的是用一种量(或一种量的一部分)来代替和它相等的另一种量(或另一种量的一部分).对于数学基本图形来讲，采用等量代换的形式，同样可以让学生将学过的知识用于解题中，能激发他们的探究能力，从而学会解决一些复杂的数学问题.比如，如图7所示，已知AB∥EC，求图形中阴影部分的面积.在指导学生解题的时候，教师要让学生多观察图形中已有的各种数学信息，将阴影部分面积转化为其他能利用已知条件的部分，进而解决问题.为此，根据题干中已知的数学信息，因为AB∥EC，所以S△AOE=S△BOC，则S阴=10×8÷2=40.在平时的初中数学几何教学中，教师可将等量代换作为一种常规的教学方法，让学生挖掘有用的信息，知道如何用一种量(或一种量的一部分)来代替和它相等的另一种量(或另一种量的一部分).在学生学习该种方法的时候，教师要鼓励学生多探究和互动，遇到难以解决的问题时，指导学生将学过的知识应用在问题解决中，还可以通过小组合作的形式来学习该种数学思想，最终提高学生的数学思维.

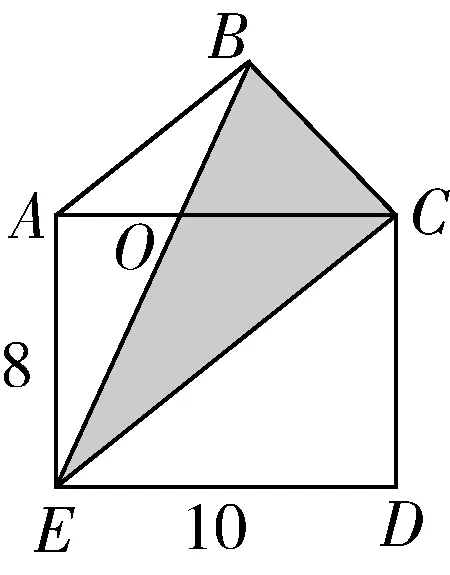
图7

结 语

综上所述，在初中几何课程中含有大量基本图形，让学生感悟基本图形的性质，学会灵活应用，对于提高他们几何解题能力的帮助是很大的.受到传统数学教学理念的影响，初中数学在培养学生解题能力中存在的问题还是较多的，如学生解题思路单一、解题灵活性不足等，这些因素限制了学生数学思维的发展.因此，在感悟基本图形，提升初中学生数学解题能力教学中，教师要以基本图形为出发点，让学生利用所给基本图形提炼出其他基本图形，学会对图形进行“累加”，从而掌握利用基本图形解题的规律，提高数学核心素养.