关于罗尔中值定理的教与学关于罗尔中值定理的教与学

◎蒋利华 陈文平 梁伍威

(桂林电子科技大学，广西 桂林 541004)

一、引言

导数的应用非常广泛，它可应用于物理学、化学、生物学、经济学以及生产实际等各个领域，而微分中值定理是导数应用的理论基础，也是导数应用教学中的重点和难点.本文以启发式教学方法介绍了中值定理的理论，还介绍了学生学习中值定理的方法，并利用中值定理解决具体的实际问题.在学习三大中值定理的过程中，教师要引导学生体会它们之间的辩证关系，一方面能激发学生的学习兴趣，培养学生的数学思维以及应用数学知识解决问题的能力，另一方面也能引导学生学会利用辩证的思维看待生活、学习中遇到的一些问题.课堂教学是培养学生能力和形成核心素养的最重要的途径，有效的课堂教学可以将复杂难学的数学理论变得易于学生理解，便于学生进行有效的学习，从而获得良好的教学效果.

二、启发式教学

启发式教学顾名思义就是一种以启发学生思考为指导思想的教学方式.它不应被理解为一种具体的教学方法或教学技巧，而是一种以启发学生探索理论知识为主，以调动学生学习积极性为宗旨，把学生的被动学习变成积极的主动学习为目标的教学指导思想.复杂的理论知识不仅会增加学生学习的难度，也会影响学生学习的积极性，为此我们可以通过启发式教学，把复杂的数学理论知识简单化，从而达到良好的教学效果.

三、罗尔定理的启发式教学

为了引起学生学习的兴趣，教师可先介绍罗尔定理的背景：罗尔在《方程的解法》一文中提出有关多项式零点分布的定理，这是现在罗尔定理的前身.当时罗尔一直在质疑微积分的正确性，所以罗尔是用纯代数的方法证明该定理的.随着微积分学的发展，人们根据微积分的理论重新证明，并把它推广到一般函数情形，才称之为罗尔定理.

下面介绍罗尔定理的内容：

定理(罗尔中值定理)若f(x)满足以下条件

(1)在闭区间[a,b]上连续;(2)在(a,b)内可导；

(3)f(a)=f(b).

为了引出定理的结果，教师应启发学生思考：定理的三个条件在几何上分别表示图像的什么特征？让学生根据图像的特征观察出定理的结论.

闭区间上连续表示图像在区间[a,b]上连续不断，没有间断点；开区间内可导是指图像在(a,b)内光滑没有尖点，并且条件f(a)=f(b)说明函数的图像在区间端点一样高，从而得到函数f(x)的图像一定具有如下的形状：

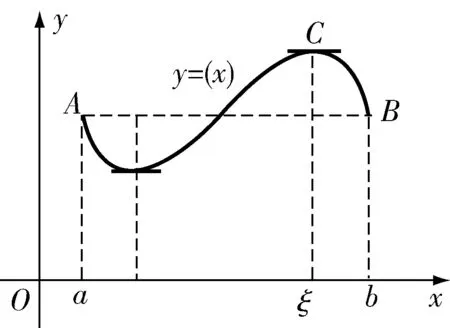
接着让学生观察思考，看他们从图像上能看到什么现象.学生很容易得到结论：函数的图像至少有一条平行于x轴的水平切线.这个结论是学生自己观察得出，这一方面激励了学生学习的主动性，另一方面也增强了学生对罗尔定理的记忆与理解.罗尔定理的完整表述为：

定理(罗尔中值定理)若f(x)满足以下条件

(1)在闭区间[a,b]上连续；(2)在(a,b)内可导；

(3)f(a)=f(b)；

则至少存在一点ξ∈(a,b)，使得f′(ξ)=0.

微分中值定理是微分学的重点、难点，定理的证明经常困扰着学生，因此在讲解定理的证明时，教师必须抽丝剥茧、层层递进，将深奥的数学定理、繁多的知识细节，融合在演绎推理过程中，让学生体会数学之美——严谨性和准确性，进而培养学生严谨客观的科学态度和勇于探索的钻研精神.

我们依然利用启发式教学介绍罗尔定理的证明过程.教师可引导学生从结论来想，定理的结论要证的是在(a,b)区间内有一阶导数为零的点，从图像上看，那个点似乎是最大值或最小值点，那么函数在[a,b]内是否有最大值和最小值呢？再看定理的条件，f(x)在闭区间[a,b]上连续可以保证其在[a,b]上有最大值和最小值(闭区间上连续函数的最值性质)，不过考虑问题要全面，一方面最大值和最小值如果相等是什么样，如果不等又如何？从而学生可得到：

(1)当最大值等于最小值时，又由f(a)=f(b)知，f(x)一定是常函数，且f(x)在(a,b)内又是可导的，故(a,b)任意一点的导数都为零.

综合(1)(2)，不难得到罗尔定理完整证明过程.

这种以学生作为主体的启发式教学模式，一方面调动了学生学习的积极主动性，培养了学生的数学思维能力，另一方面也把复杂的数学理论知识简单化，简化了学生的学习过程，即能达到良好的教学效果，又能让学生获得良好的学习效果.

罗尔中值定理的推论.

推论1如果F(x)在区间I上可导，且F′(x)=0，则F(x)≡C.

推论2如果F(x),G(x)在区间I上可导，且F′(x)=G′(x)，则F(x)=G(x)+C.

四、罗尔定理的应用案例

例1设f(x)满足以下条件

近年来，华中师范大学不断深化体制改革，完善监管机制。2014年7月，该校后勤集团在运行机制和体制上作出了重大调整，设立4个办公室、7个实体中心，实行小机关大实体运行模式。为了强化部门负责人、生产者是第一责任人的意识，该校成立了食品药品工作站，并于2014年11月正式挂牌。“工作站由校办牵头，挂靠后勤保障部，同时配套专职监督员1人、信息报送点20多个，形成信息报送网格化，在全省率先完成了食品药品监管体制的建设。”该校相关负责人说。

(1)f(x)在闭区间[0,a]上连续；(2)f(x)在(0,a)内可导;(3)f(a)=0；证明：在(0,a)内至少存在一点ξ，满足ξf′(ξ)=-f(ξ).

分析引导学生明确，此题要证明的是ξf′(ξ)= -f(ξ)，

即ξf′(ξ) +f(ξ)= 0，也就是F′(ξ)=ξf′(ξ) +f(ξ)=0.

而后利用罗尔中值定理即可证明.

证明构造辅助函数F(x)=xf(x)，显见(1)F(x)在闭区间[0,a]上连续；(2)F(x)在(0,a)内可导;(3)F(0)=0=F(a)=af(a)；由罗尔中值定理知，在(0,a)内至少存在一点ξ，使得F′(ξ)=0,即ξf′(ξ)=-f(ξ).

例2若f(x)满足f′(x)=f(x)，f(0)=1，证明：f(x)=ex.

分析由结果f(x)=ex出发思考，相当于证f(x)e-x=1，反过来找条件，由f′(x)=f(x)知e-x[f′(x)-f(x)】=0，即F′(x)=[e-xf(x)]′=0，则F(x)≡C.从而利用罗尔中值定理的推论就可得到对应的结果.

证明构造辅助函数F(x)=e-xf(x)，显见F(x)∈D(-∞,+∞)，且F′(x)=[e-xf(x)]′=e-x[f′(x)-f(x)]=0，所以F(x)≡c，又F(0)=f(0)=1，故F(x)=e-xf(x)=1，即f(x)=ex.

例3若a0xn+a1xn-1+…+an-1x=0有一个正根x0，

证明：方程na0xn-1+(n-1)a1xn-2+…+an-1=0必有一个小于x0的正根.

分析这是一个证明方程有实根的问题，而罗尔定理的结论相当于f′(x)=0在(a,b)内至少有一个实根.

证明令f(x)=a0xn+a1xn-1+…+an-1x，显见f(x)在[0,x0]内连续，在(0,x0)内可导，且f(0)=f(x0)=0，由罗尔中值定理知在(0,x0)至少存在一点ξ，使得f′(ξ)=0，即na0xn-1+(n-1)a1xn-2+…+an-1=0必有一个小于x0的正根.

五、教学效果体现

对于桂林电子科技大学商学院20级管理科学与工程类专业的学生，教师在进行《高等数学》上册的教学过程中，就利用了启发式教学模式，该班学生在期末全校统考中取得了不错的成绩，高等数学的通过率从以前的百分之七八十提升到了百分之九十.

六、罗尔中值定理的应用展望

(一)罗尔中值定理推广形式探讨

罗尔中值定理在高等数学这门学科中扮演着举足轻重的角色，一旦学生能够熟练掌握和应用这些知识，可以获得一种满满的成就感.而导数作为一种重要数学工具，在分析和探讨函数性质和各个函数之间映射关系方面发挥出重要作用.但是，仅仅从导数这一概念入手去分析和研究函数，还不足以有效地突出导数这一工具的应用价值.为了解决这一问题，教师需要将导数建立在微分学相关基本定理的基础上进行应用，微分学相关基本定理主要包含广义罗尔中值定理 、拉格朗日定理等.而这些基本定理被统称为“微分中值定理”，在这些中值定理中，罗尔定理属于一种比较常用的定理，其通过采用推广延伸的方式 ，可以从自身延伸出其他比较重要的定理，从而实现对罗尔中值定理的有效推广和补充.另外，拉格朗日定理的应用也充分体现出了微分学的典型应用，该定理可以为函数和导数之间的有效连接起到一定的桥梁作用，从而取得良好的沟通效果.此外，以上定理作为一种科学工具，为分析和探究各个函数映射关系提供了重要支持，所以，对罗尔中值定理推广形式的探讨，除了可以直观、形象地体现出罗尔中值定理在高等教育中的典型应用外，还能为进一步提高函数关系研究结果的精确性打下坚实的基础.

(二)罗尔中值定理推广应用分析

在分析和应用罗尔中值定理期间，为了进一步提升高等数学教学水平，教师需要在参照广义罗尔定理的基础上， 通过增加和设置有限区间相关条件，可以得到罗尔中值定理相关理论知识，该理论知识主要是参照应用型函数可导性所研发的，为后期全面地分析和研究函数整体形态打下坚实的基础.由于广义的罗尔定理在具体的使用中，存在条件性太强问题，因此，其应用到实践中往往会面临较大的困难，也会增加学生的学习和理解难度.同时，由于受条件的限制，学生很容易在实际学习期间遇到瓶颈.这些因素对罗尔中值定理在实践中的应用产生了一定的限制作用.为了解决这一问题，确保罗尔中值定理可以更好地应用于函数映射关系的处理中，教师需要在不断提高罗尔定理的灵活性和可理解性等特点的基础上，充分结合广义罗尔定理相关理论知识，不断增加罗尔中值定理推广研究深度.此外，教师还要不断地开拓自身的思维，突破研究相关的各种局限性条件，从而实现对开区间、闭区间的深入分析和探究，从而起到拓展罗尔中值定理相关理论知识的作用.此外，教师在应用罗尔中值定理对各种函数类进行分析和研究期间，要尽可能地降低和削弱相关条件限制，确保罗尔中值定理得以推广和应用.

七、结论

高等数学教学内容的主要特点是具有高度的抽象性，这种高度的抽象内容使高等数学的教学与学习都相对变得困难.所以，教师在高等数学的教学过程中如何利用启发式教学模式直接影响到教学效果和学生的学习效果.高等数学教学的主要目的是培养学生的数学思维能力和解决具体问题的能力，教师只有通过启发式教学才能激发学生学习的兴趣和主动性，从而达到培养学生学会思考问题，提升解决问题的能力的根本目标.