面积法在二次函数综合性问题中的应用探究

朱玉杰

（上海市格致初级中学）

在中学数学教学中，学生通过对面积和面积法的学习，一方面，能更直观地理解和掌握几何知识；另一方面，可通过数形结合，对一些较为抽象的代数知识具象、直观地进行解释和学习.面积法既可以用来计算平面几何图形的大小，又可以把面积作为桥梁解决一些非面积类问题.例如，利用面积关系来说明数学中的一些恒等式、不等式或证明一些定理等，同时也利用数形结合思想构建数学模型，强化学生对数学知识的理解，提升应用数学知识解决问题的能力.本文结合笔者的教学实践经验，主要阐述面积法在二次函数综合题中的一些应用.

一、平面直角坐标系下求三角形面积的基本方法

平面直角坐标系中函数的综合性问题大多研究函数的性质及函数图象上特殊位置的点所构成的特殊图形的属性及性质.而平面几何图形面积的考查以三角形面积最为常见，且应用广泛.已知三个顶点坐标求三角形面积是该类问题的基础题型，笔者结合一道题目阐述几种常用的计算方法.

例1如图1，已知A（0，-2），B（4，2），C（2，6），求S△ABC.

图1

解法大致分为两类：（1）直接法；（2）间接法.

1.直接法

解：如图2，设CD=x，

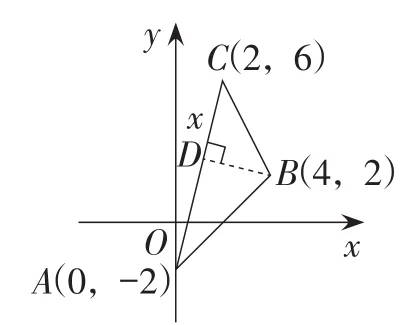
图2

2.间接法

该方法可分为三类：（1）割形；（2）补形；（3）等积转换.

（1）割形.

一般有两种割法：水平方向割（如图3）和铅垂方向割（如图4），即过三角形的一顶点作关于坐标轴的平行线（称为割线），将原三角形分割成两个底边相同的三角形，其关键在于求割线与原三角形一边的交点坐标.总结规律可得出（如图5）.

图3

图4

图5

（2）补形.

根据图形特征将不规则图形补成规则图形，是用规则图形的性质来解决问题的一种方法.补形方式多种多样，仅罗列三种类型加以说明如图6～8所示.

图6

图7

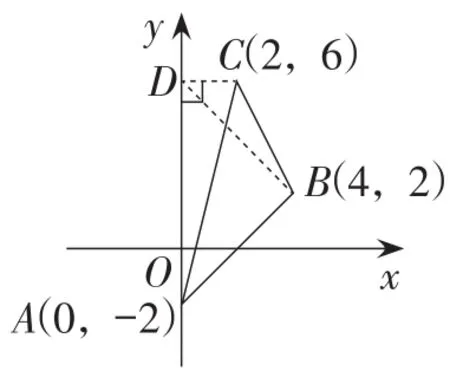
图8

（3）等积转换.

解：如图9，过点C作CD∥AB，

图9

则S△ABC=S△ABD.

易得直线CD的表达式为y=x+4.

则D(0，4 )，S△ABC=S△ABD=12.

【评析】以上的等积转换法是过三角形的一个顶点作对边的平行线，在平行线上任取一点，构造与原三角形同底等高的三角形.教师可有意识地引导学生找寻平行线与坐标轴的交点（如图9），或与平行于坐标轴的直线的交点作为新三角形的顶点（如图10），也可以将三角形面积转换成平行四边形面积的一半来求解（如图11）.

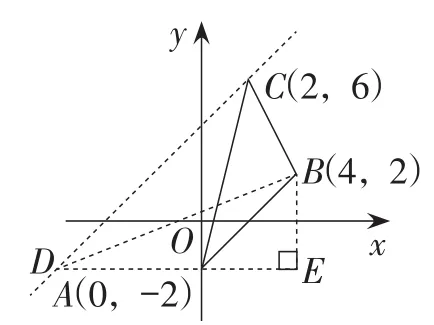
图10

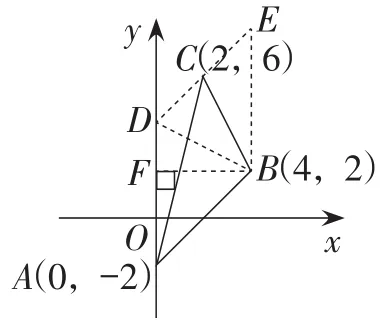
图11

二、面积法在二次函数综合题中的应用

例2如图12，已知平面直角坐标系xOy，抛物线y=x2+6x+8与直线y=x+4交于点A(- 4，0)和B(- 1，3)，直线y=x+4与y轴交于点D(0，4)，抛物线y=x2+6x+8与x轴交于另一点C(- 2，0)，顶点为点E(- 3，-1).

图12

1.利用面积法求解锐角三角函数

问题1：如图13，连接BC，CD，求sin∠BCD的值.

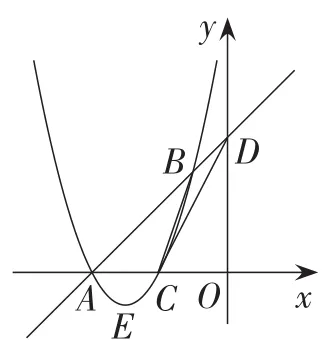
图13

解析：已知△BCD的三个顶点坐标，三角形的三边长确定，则三角形的形状和大小确定.则三角形的边角关系及面积等属性均确定（如图14）.

图14

可通过面积割补的方法求得S△BCD=S△ACD-S△ABC=4-3=1.再利用面积公式求得.

2.利用面积法解相似三角形存在性问题

问题2：在y轴上存在一点P，使△CDP与△CBA相似，求点P的坐标.

解析：二次函数背景下相似三角形存在性问题考查学生对综合知识的运用能力，涉及二次函数的图象与性质、相似三角形的判定及性质、锐角三角函数等知识点.一般可分为两种题型：一动一定型（一个三角形确定，另一个三角形待定）和双动型（两个三角形均随点的移动而变化）.在此主要阐述用面积法解决“一动一定型”相似三角形存在性问题.这类问题的一般特征是：①两个三角形相似，一个三角形的三边确定，称为确定三角形，另一个三角形的一边及一角确定，称为待定三角形；②待定三角形的定角（或其补角）是相似三角形的对应等角.

图15

3.利用面积法解特殊位置点的坐标

问题3：在抛物线上是否存在一点K，使S△KCD=1，求点K的坐标.

解析：问题3属于确定（已知坐标）三角形的两点，求特殊位置的第三点坐标的一类题型.利用特殊形式的面积法进行转换，可回避繁杂的计算，将复杂问题简单化.

策略1：逆用割形.

如图16，作KG⊥Ox，交CD于点G.

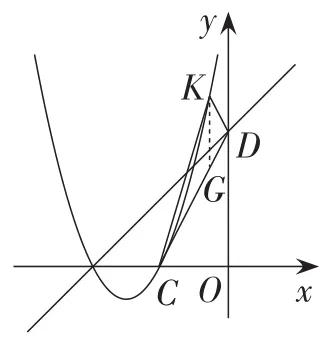
图16

易得直线CD的表达式为y=2x+4.

设K(m，m2+6m+8)，G(m，2m+4)，

则KG=m2+4m+4.

得m1=-1，m2=-3.

所以K1(- 1，3)或K2(- 3，-1).

策略2：逆用补形.

如图17，连接KO，

图17

策略3：逆用等积转换.

如图18，过点K作KG∥CD，交x轴于点G.

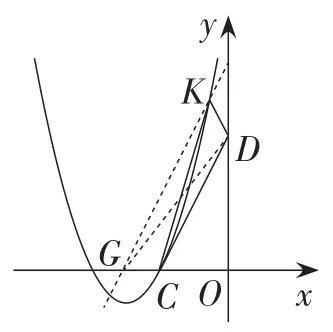
图18

由题意知，S△GCD=S△KCD=1.

易求得直线KG的表达式为y=2x+5，与抛物线y=x2+6x+8联立，解得m1=-1，m2=-3.

所以K1(- 1，3)或K2(- 3，-1).

4.利用面积法解定角的存在性问题

问题4：如图19，抛物线与x轴交于另一点C，连接DC，点P在抛物线的对称轴上，且在第二象限内，使∠ADC=∠ADP，求点P的坐标.

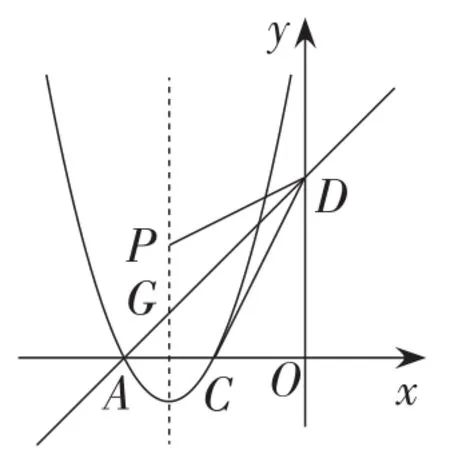
图19

解析：定角存在性问题，主要指的是在平面直角坐标系中存在定角（特指满足已知这个角或其补角的锐角三角函数的角），求特殊位置点的坐标的一类题型.

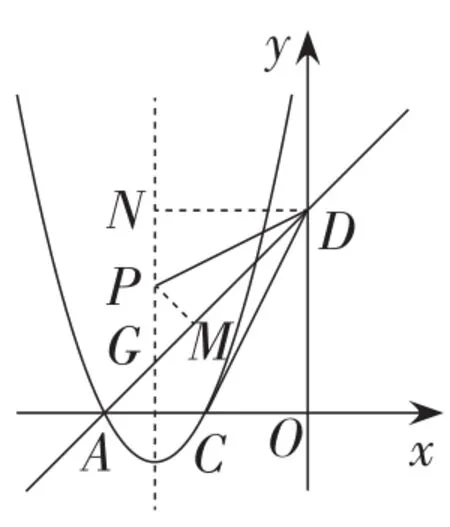
图20

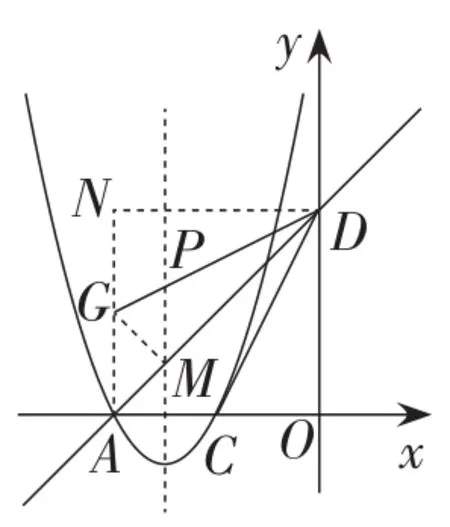
图21

图22

5.利用面积法解线段之比的相关问题

问题5：在对称轴左侧抛物线上存在一点P，连接EP交直线AD于点Q，满足，求点P的坐标.

解析：利用构造平行线进行三角形面积等积转换解决此题.如图23，S△MAQ=S△PAQ，S△CAQ=S△EAQ，再利用“同高三角形面积比等于底之比”将线段之比与三角形面积之比建立联系，即由AC=2，得MA=4.进而求得直线PM的表达式为y=x+8，与抛物线y=x2+6x+8联立，解得P(- 5，3).

图23

三、面积法的解题功能

1.数学建模，提升学生分析问题的能力

张景中院士曾提到，面积法不仅仅是解题的利器，而且是建立初等数学体系的中央枢纽.可见面积法在初等数学中起到一个贯穿知识体系的作用.因此，我们要引导学生构建基本的数学模型.当题目中的已知元素可以确定三角形，则这个三角形的内在属性均已确定，我们就可以利用面积法求得三角形中其他未知的元素，即数量关系的确定决定了位置关系，而位置关系的确定可推导出新的数量关系（如图24），面积法只是数量关系之间推导的一种方式.数学模型的建立，能够帮助学生理解知识之间的内在联系，提升学生分析问题的能力.同时，也要打破固性思维，面积法并非是万能的，仅是解决部分数学问题的一个工具，甚至也并非是部分题目的最优解.在教学过程中，教师不可过于夸大面积法的认知地位，使学生陷入误区.

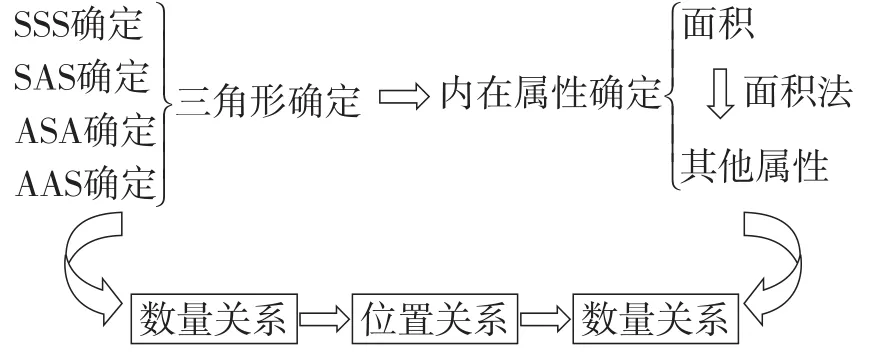
图24

2.数形结合，培养学生的数学核心素养

三角形的边角数量关系决定了位置关系的确定，位置关系又导致新的数量关系的产生，数量关系与位置关系的相互转换，体现了数形结合思想.通过对图形进行割补与拼接，以及面积之间的等积转换，实现图形性质的相互转化，感受演绎推理的思路来源于图形的转化过程，将抽象的数学可视化、具体化，培养学生学会用直观的图象说明抽象的数学知识，找到图形与图形之间、位置关系与数量关系之间的内在联系，把握数学的本质，多角度提升学生的几何直观与抽象能力.笛卡儿的《方法论》中指出，从最简单、最容易认识的对象，一点一点上升到复杂的对象的认识，是任何领域获得正确知识的主要原则.面积法解决数学问题体现了逻辑推理的核心，即理性思维，既体现了推理的严谨性，又体现了推理的灵活性.数学运算与数据分析是解决数学问题的基本手段，是学生学好数学的基础，体现了学生的数学素养.应用面积法解题不仅能锻炼学生数学运算与数据分析的能力，又能帮助学生养成程序化思考问题的习惯，形成严谨求实、一丝不苟的科学精神.

3.知识迁移，注重学生发散性思维的培养

知识迁移是指在连续学习过程中学习者在已经具有的知识经验和认知结构、已获得的动作技能、习得的态度等基础上进行新知识再学习的过程.在日常教学过程中，教师应注重知识之间的联系，培养学生知识迁移的能力.几何图形的变化方式多种多样，再结合函数背景，使得图形关系错综复杂，但其中基本图形及图形的内在属性的对应关系却万变不离其宗，而这些隐含在复杂图形中的基本图形是解决复杂几何问题的工具.从求三角形面积的方法分析迁移到利用面积法解决综合性问题，从利用面积法解决面积问题迁移到利用面积法解决多种问题，乃至迁移到生活应用类综合性问题的学习过程，是学生训练发散性思维的过程.

面积法在初中阶段的应用非常广泛，在平面直角坐标系下的综合应用只是其冰山一角.在日常教学过程中，教师不仅要重视面积法的解题功能，也要关注其育人功能，利用面积法建立初等数学体系的中央枢纽.