基于非齐次复合Poisson过程的正交异性钢桥面板细节疲劳裂纹随机扩展研究

张海萍, 刘 扬, 罗 媛, 郑 辉, 邓 扬

(1.湖南工业大学 土木工程学院，株洲 412007;2.北京建筑大学 土木与交通工程学院，北京 100044)

1 引 言

研究表明钢桥面板细节的疲劳失效过程呈现非线性变化[1]。变幅荷载、超载和荷载顺序均会影响疲劳裂纹的扩展行为。实际车辆运营状态是一种复杂的随机过程[2]， 使得车载下钢桥面板细节点的疲劳裂纹扩展随机性增强。钢桥面板细节疲劳随机扩展分析方法亟待发展。

近年来，部分研究学者采用随机车流描述车辆的运营状态[3]，其核心思想是基于车流统计数据对车型比例、车重、车距和车速等参数的概率模型进行建模，并采用蒙特卡洛(Monte-Carlo)法对相关参数概率模型进行抽样，最后整合所有的抽样数据得到随机车流样本。随机车流模型没有考虑车流在时间维度上的变化，实为伪随机过程模型。在车辆荷载随机模型研究方面，主要采用单一的白噪音模型[4]、平衡更新模型[5]和泊松过程模型[6]来描述车辆的随机过程。单一的数学随机过程模型忽略了驾驶人员行为和交通规则，使得数值模型与车辆实际运营状态存在一定的差异。

现阶段，钢桥的疲劳评估方法主要包含疲劳强度曲线法(S-N曲线法)和断裂力学法。S-N曲线法研究工作的趋势是通过量化不同标准材料、结构和细节类型疲劳试验，丰富和完善工程结构的疲劳强度规范[7]。很多学者认为，名义应力法并不适用于正交异性钢桥面结构的评估。不少学者通过多次对细节及周围点的测量应力进行求商来确定热点应力系数。如朱太勇等[8]提出一种全空间S-N曲线法，该疲劳强度曲线能够考虑OSD细节热点应力和焊接残余应力对疲劳寿命的影响。S-N曲线的局限性在于无法考虑随机应力幅和超载应力幅对裂纹扩展的影响，从而无法分析疲劳裂纹的非线性扩展过程。对比S-N曲线法，断裂力学能够分析结构或材料疲劳损伤的非线性变化过程，更符合金属材料疲劳损伤的演化规律。但由于实际工作结构的裂纹形状不规则和疲劳应力幅形式复杂，使得实际工程结构细节的应力强度因子求解困难。

本文建立了一套应用于桥梁结构细节疲劳裂纹随机扩展评估方法的理论框架。首先，提出了一种非齐次复合泊松过程随机模型描述车辆的随机运营过程。该模型包含有车流密度、车辆类型、车重和车速等参数。在ANSYS平台将车流的随机荷载时间序列数据转换成疲劳应力时间序列。提出了能够考虑加载次序和超载因素OSD焊接细节的疲劳评估方法，并讨论不同车辆排队顺序与车辆超载率对疲劳开裂扩展速率的影响。

2 车辆荷载非齐次复合Poisson过程建模

2.1 车辆随机过程模型

车辆在特定的时间经过某桥梁的某一位置后，车重的时间序列为一种脉冲曲线。车辆数的时间序列随时间的累计呈现出阶梯上升的特征。车重和车辆数是决定细节疲劳开裂扩展的关键变量。复合Poisson过程与车流过桥特征高度相似。可以考虑用滤过复合Poisson过程模型描述车辆运营过程。用复合Poisson过程随机模型描述车辆荷载需要满足三个条件。

(1) 车辆重w(t)和车数在时间区间[0，T]具有相同概率分布特征。

(2) 复合Poisson过程模型只能描述单一车道的车辆运营。

(3) 车辆荷载在时间区间[0，T]内保持匀速。复合Poisson过程模型的表达式为[9]

(1)

式中N(t)为在时间区间[0，T]以速率为λ的Poisson过程，ζn为第n辆货车的重量，τn为第n辆货车跨越测量点所需的时间，Tn为第n-1辆到达车辆与第n辆到达车辆的时间间隔。I(t;τn)的表达式为

(2)

由图1可知，高速公路车辆运营车流量随时间变化呈一定的规律性。在9时～18时车流密度相对区间0时～8时较高。实际运营的车流密度不满足Poisson过程条件假设(1)，即车流密度在时间跨度为1天内变化较大。需要将时间区间长度按照实际车流密度在时间上的变化来进行划分。可以将模型中的时间区间等分成M段，每一段的车辆密度强度参数取值均不同。复合Poisson过程的另一个参数ζn会随车型的变化概率分布有较大的不同。可以看出，用传统的复合Poisson过程模型来描述车辆荷载随机过程假设太多，难以满足工程应用的要求。需要建立一种广义符合实际车辆运营状态的数值模型-非齐次复合Poisson模型。该模型将不同时段的车流密度强度的Poisson模型组合在一起，并能够将车重按照车型分类分别建立概率模型，其表达式为

(3)

式中M为日交通车流时间区间分段数，Ni(t)为时间区间[Ti - 1,Ti]的复合Poisson过程模型，其车流密度强度参数为λi(t),ζj n为车辆中第n辆j型车，τj n为第n辆j型车通过称重传感器的时长。

2.2 随机模型参数

2.2.1 时间区间

参数M代表非齐次复合Poisson模型中子复合随机模型的个数。M的取值越大，划分的时间区间则越多，模型越精确同时也越复杂。M的取值需要依据实际车流密度的实时统计曲线来确定。文献[10]统计了2014年南溪长江大桥的日交通流均值分布数据(图1)。由图1可知，车流密度在0时～7时区间保持恒定的疏松交通运营状态，可以作为第一个子区间。在7时～10时段，车流量呈直线上升的趋势，作为第二个时间子区间。车流密度在10时～18时时间区间维持在一个较高的密度运营状态，将其划分为第三个时间区间。在时间区间18时～24时，车流密度直线下降，可以将其作为第四个时间区间。综上所述，本文将车辆荷载非齐次复合Poisson模型的参数M取值4。

2.2.2 时间间隔

λi为时间区间[Ti - 1,Ti]的车流密度强度。T的概率分布决定了车辆荷载随机过程模型的类型。本文假定车流随机过程模型用Poisson模型来描述，则时间T服从指数分布，概率密度函数可表示为

(4)

式中λi为指数分布的强度值。从图1可以看出，强度系数λi随时间呈一定的变化规律。将车流荷载随机过程的时间区间分为[0，7],[7，10],[10，18]和[18，24]4个区间。分别统计时间区间[0，7]和[10，18]车辆时间间隔T的概率分布，并采用指数分布拟合实测分布模型。图2给出了两个代表时段的实测统计分布与拟合模型的对比。采用分段函数来描述4个区间的强度系数λi，其表达式为

(5)

图2 两时段车辆时间间距概率分布Fig.3 Vehicle time interval probability distribution in two differences period of time

2.2.3 车型和车重

(1) 车型

不同车辆类型其车重的概率分布有所不同，将车辆类型按照车辆轮轴数分为5类， 图3为5类典型车型日平均交通占用率。其中偶数车轴的车占据总重车交通比例的91%。奇数车轴占据交通总量比例的9%。

图3 5类典型车型占有率Fig.3 Occupation ratio of five types of vehicles

(2) 车重

车辆荷载母样本监测数据包含不同车型和车辆货载率，车辆荷载服从高斯混合分布，则

(6)

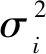
表1 车重高斯混合模型参数Tab.1 GMM parameters of vehicle weight

2.2.4 时间参数τj n

τj n代表车辆荷载经历指定点所需要的时间，可以用总轴长与车速的比值来定义,即

τj n=lj n/vj n

(7)

式中lj n和vj n分别为第n辆j型车经历的总轴长和车速。Guo等[11]认为车辆的轴长服从对数正态分布。同时，对数正态分布模型也可以用来描述车速的概率分布[12]。假设车辆的总轴长与车速的概率模型相互独立，由经典统计数学理论可知推导时间参数τj n服从对数正态分布。表2列出了时间参数τj n的拟合模型参数。

表2 时间参数τj n对数正态模型拟合参数Tab.2 Parameters of τj n Log-normal model

2.4 疲劳应力随机过程

荷载模型需要转换成细节疲劳效应模型才能完成对结构细节疲劳裂纹随机扩展的预测。对于车辆荷载随机过程模型，包含3个关键的参数,即相邻两车的时间间距T、车辆经过测点的时间τj n和车的总重ζn。对于结构的荷载效应随机过程模型，两次脉冲效应的时间间距与相邻两车的时间间距T相对应。任意一次脉冲效应的持续时间与车辆经过测点的时间τj n相对应。采用瞬态分析将荷载转化成结构的疲劳应力。细节的疲劳应力随机过程模型可表示为

(8)

式中F(ζj n,Te)为当铺装层温度为Te时，车辆荷载ζj n作用下结构细节点应力的时间序列。

为实现荷载与应力效应之间的转化，在ANSYS平台建立正交异性钢箱梁结构的局部模型。由于局部模型单元划分数量较多，为减少计算量，建立半幅钢箱梁有限元模型。采用solid45单元和shell63单元分别模拟正交异性箱梁结构的沥青混凝土铺装层和钢箱梁正交异性板。对沥青混凝土铺装层、顶板、底板和U肋采用矩形进行网格划分，横隔板采用三角形进行网格划分。假设主梁结构在承受车辆荷载时不发生滑动位移和扭转，有限元模型边界节点的6个自由度全部约束。铺装层温度为20 ℃时，沥青混凝土的弹性模量和泊松比分别为6147 MPa和0.2。U肋的顶板、腹板和底板厚度分别为14 mm,8 mm和10 mm。U肋的弹性模量和泊松比分别为210 GPa和0.3。主梁的局部有限元模型如图4所示。

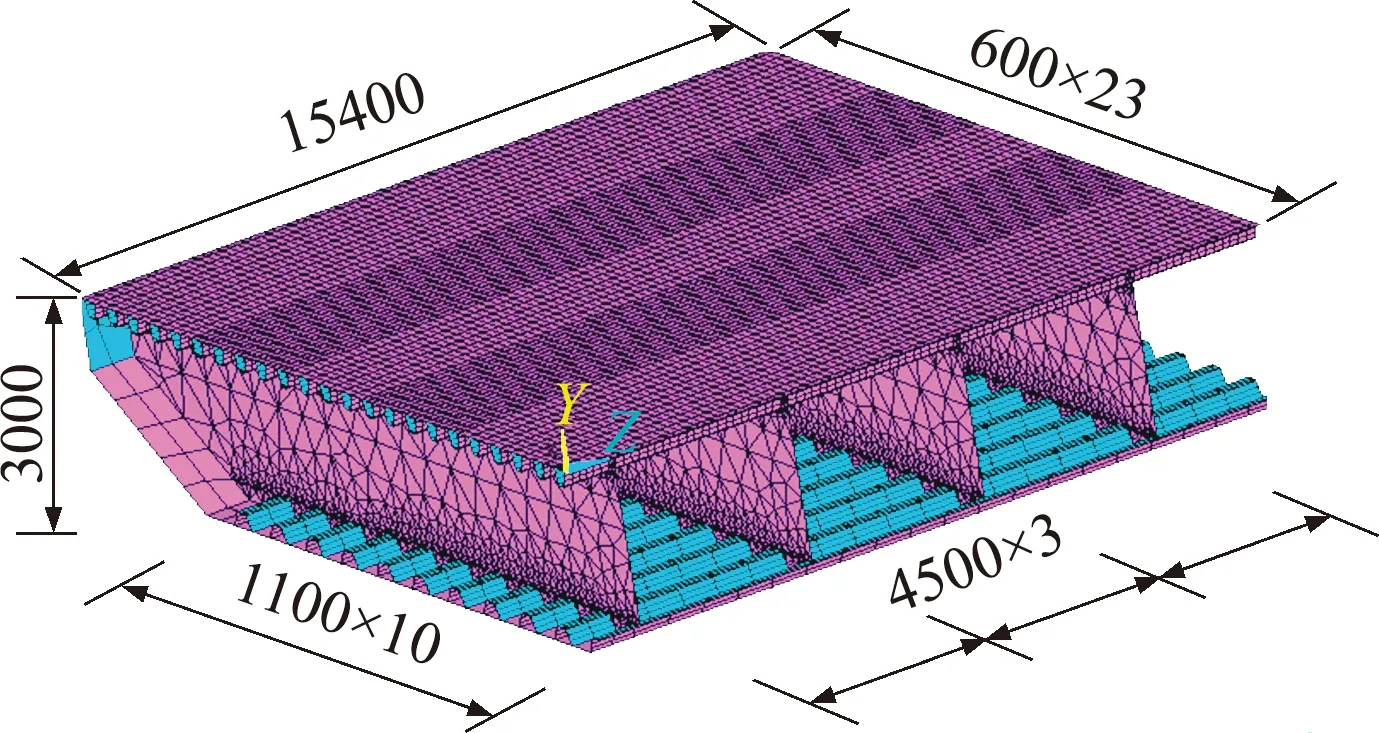
图4 桥面板有限元模型Fig.4 Finite model of steel box girder

图5给出了V4过桥时U肋-顶板细节的疲劳应力模拟曲线与应力实测曲线对比。可以看出，模拟曲线和实测曲线整体拟合较好，表明有限元模型满足计算精度要求。

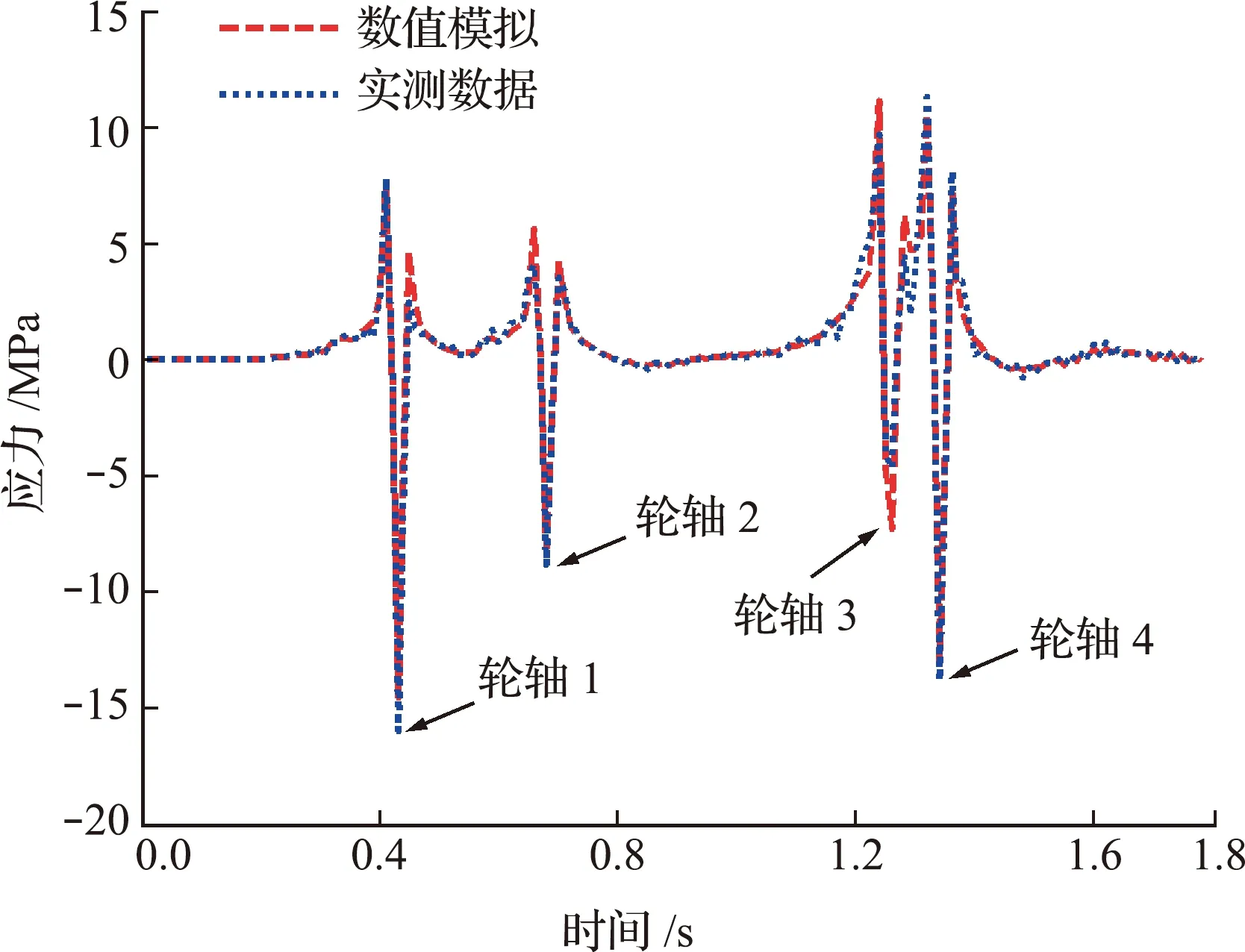
图5 数值模拟和实测数据应力时程曲线对比Fig.5 Comparisons between the measured stress data and FEA results

3 疲劳裂纹随机扩展模型

S -N 曲线法不能考虑材料疲劳开裂的过程，Paris等[13]提出了疲劳裂纹开展模型

da/dN=C·ΔKm

(9)

式中C和m为材料参数，a为材料的疲劳裂纹尺寸，ΔK为疲劳裂纹尖端附近的应力强度因子。该模型简单描述了裂纹扩展与应力强度因子之间的发展关系，Paris模型只能计算恒定应力幅作用下的裂纹扩展行为，不能预测变幅作用下结构的疲劳寿命。Elber[14]认为材料的裂纹张开需要一定的门槛应力，当循环应力大于开口应力时，裂纹才会开口，且裂纹尖端才会向前扩展。提出有效应力强度因子的表达式为

ΔKeff=ΔK-ΔKo p

(10)

式中 ΔKeff为有效应力强度因子，ΔKo p为开口应力强度因子。

图6给出了材料裂纹从t时刻到t+Δt时刻裂纹扩展的过程。在扩展过程中，材料的疲劳裂纹尖端从点O扩展至点O′，裂纹尖端的位移为da，裂纹的张开位移为dδ，t+Δt时刻裂纹的张开角度为θ。可推导裂纹的扩展位移da和裂纹的张开位移dδ之间的关系式为

(11)

文献[15]通过试验观测得到疲劳裂纹的张开角度变化范围从初始裂纹的90°到疲劳失效时的4°～6°。裂纹的张开角度与材料裂纹尖端的应力强度因子ΔK、材料屈服强度应力因子ΔKc和材料裂纹开口应力强度因子ΔKo p存在相关关系，其表达式为[16]

(12)

式中 当细节承担的应力等于材料的开口应力时，则裂纹张开角度为90°；当效应应力等于材料的屈服应力时，裂纹张开角度为0°。

图6 半椭圆疲劳裂纹扩展Fig.6 Illustration of semi-elliptic fatigue crack propagation

正交异性板焊接细节点出现疲劳裂纹主要集中在有初始缺陷的部位，属于表面裂纹，故裂纹张开位移的表达式为[17]

(13)

式中E为材料的弹性模量，σy为材料的屈服应力。为进一步简化计算表达式，令

(14)

则结合式(11～14)，得到在时间t和t+Δt时刻，裂纹张开位移和裂纹深度的关系式为

δ=λσ2a,δ′=λ(σ+dσ)2(a+da)

(15,16)

对式(15,16)求差，得到

dδ=δ′-δ=λ(2σadσ+σ2da)

(17)

将式(17)代入式(11)，得

(18)

式(18)表达出了微元时间内应力变化引起裂纹尖端尺寸向前扩展的变化值的对应关系。从时间t到t+Δt内，疲劳裂纹尺寸增长长度的表达式为

(19)

参数E，σy和Kc均为材料的固有特征参数值，不随外界荷载或环境的变化而变化。表3列出了3个参数的取值。a(t)为t时刻材料的椭圆形疲劳裂纹的长轴取值，也就是描述疲劳损伤大小的参数。当t=0时，a(0)的取值为材料的初始缺陷裂纹尺寸。通过对现场的测量或假设得到。本文假设初始裂纹长轴长度值为0.1[18]。σ(t)为结构材料关注点应力随时间的变化值。

表3 疲劳参数取值[19]Tab.3 Value of fatigue parameters[19]

开口应力强度因子Ko p和有效应力强度因子ΔKeff作为式(19)的两个复杂的参数变量需要进行详细讨论。根据正交异性板细节点的受力特点，主要受拉压作用，故I型裂纹为最危险的裂纹形态[20]。本文选用I型裂纹作为疲劳裂纹的形态。应力强度因子的表达式为[21]

(20)

式中F(a)为裂纹的形状函数。F(a)的表达式由裂纹的几何形状决定。文献[22]给出了形函数的一般表达式为

F(a)=M1M2/P

(21)

式中M1和M2分别为裂纹表面修正系数和材料厚度修正系数,P为形状参数。

M1=1+0.12 [1-a/(2c)]2

(22)

M2=2w/(πa)·tan[πa/(2w)]1/2

(23)

(24)

式中a和c分别为半椭圆裂纹的裂纹深度和裂纹宽度，w为材料的厚度，θ为裂纹的张开角。本文假设半椭圆的短长轴比值恒定，参考文献[23]的测量值a/c=0.1，则应力强度因子的一般式为

(25)

式(25)给出了正交异性板两类焊接细节构造应力强度系数的一般表达。对于开口应力强度因子Ko p所对应的开口应力σo p需要确定。在恒幅荷载作用下，同一材料的疲劳裂纹开口应力保持不变。当荷载形式为变幅时，则材料的开口应力随荷载不同而改变。文献[24]认为裂纹在一个循环荷载作用结束后，裂纹从张开到闭合的过程中，会在裂纹尖端产生椭圆形的反塑性区域。当下一轮循环荷载作用时，拉应力使得裂纹尖端出现塑性区域的面积等于前一轮荷载造成的反塑性区域面积时，裂纹尖端才会从新张开[25]。反塑性区和塑性区概念的提出解释了变幅荷载为何能够引起材料裂纹开口应力的变化。文献[26]给出反塑性区域半径的计算表达式为

在Bb平台选课数量上，超过50%的学生在Bb平台中学习过3-4门课程。从学生日常登陆Bb平台学习的次数看，有26.6%的学生积极参与Bb平台学习；基本不登陆和每月仅登陆1-2次的学生有163人，占比73.4%。学校将进一步完善和丰富Bb平台上的课程建设和课程内容，让学生在移动学习中学有所得，感受到乐趣，加强学习效果。

(26)

式中rp为反塑性区域椭圆的长轴。

拉应力作用下，裂纹尖端的塑性区域面积大小为[27]

(27)

式中

(28)

当反塑性区域半径rp等于塑性区域半径rf时，裂纹尖端开始向前扩展。结合式(26,27)，推导得到第i次开口应力的表达式为

(29)

式中σi o p为第i次疲劳裂纹的开口应力，σi min为第i次循环应力的最小值，Δσi - 1为第i-1次应力幅值。由式(29)可知，当前疲劳裂纹的开口应力与前一次的应力幅值关系密切。前一次应力幅值越大，当前的开口应力也就越大。值得说明的是，当i=1时，依据式(29)可推导开口应力σi o p=σi min。若σi min≤0，则式(29)不成立。故式(29)成立的边界条件为i>1。图7为两类疲劳裂纹尖端塑性面积区间对比。

图7 疲劳荷载作用下裂纹尖端的两塑性区间面积Fig.7 Two types of plastic zone under the cycle loading

由式(19)可知裂纹尖端扩展过程为一种随机过程模型。基于桥梁健康监测数据和有限元计算数据对OSD两类典型的细节疲劳裂纹随机扩展模型进行讨论。疲劳裂纹的扩展随机性很强，不能用单一的裂纹扩展曲线来代表细节的裂纹扩展情况。图8列出了100次细节疲劳裂纹扩展的三个特征值的变化曲线。三个特征值分别为5%分位值点、均值点和95%分位值点。当桥梁结构服役163.3年时，细节点的疲劳裂纹深度均值达到顶板的厚度。在桥梁服役年限区间[158.5,170.1]，细节点的疲劳失效概率为90%。

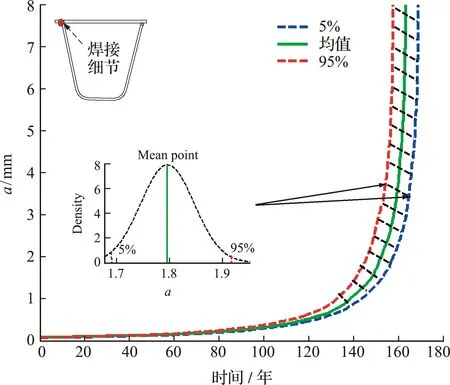
图8 细节疲劳裂纹随机扩展Fig.8 Illustration of fatigue crack random propagation for details

4 讨 论

4.1 不同车辆加载次序下疲劳裂纹随机扩展

工况1的车辆荷载加载次序遵循从大到小的原则，车辆加载次序依次为V6,V5,V4,V3和V2；工况2则与工况1相反；工况3的加载次序介于工况1和工况2之间，加载次序依次为V3,V5,V6,V4和V2。车辆的车重和轴重按照标准疲劳车辆取值。由图9可知，工况1、工况2和工况3作用下，细节点的疲劳寿命分别为1062000,1124000和1165000次工况循环加载次。在3类工况中，工况1和工况2作用下的细节疲劳寿命最短和最长。在荷载应力幅和加载次数相同的情况下，两种工况作用下细节点的疲劳寿命相差了8.8%。重载车辆排序靠前，能够使得疲劳裂纹在初期得到迅速扩展。由于变量a在前期得到较快的增长，使得在后期轻载车辆加载时裂纹尖端应力强度因子仍能达到较高的水平，裂纹扩展速率能够保持在较高的水平。

图9 不同工况作用下细节点的裂纹扩展曲线Fig.9 Crack propagation under different vehicle loading sequences

4.2 车辆超载作用下的裂纹扩展模型

(30)

式中PO L，σO L和KO L分别为超载对应的荷载、应力和应力强度因子。Pe q m,σe q m和Ke q m则为等效荷载、等效应力幅和等效应力强度因子。等效荷载Pe q m的表达式为[29]

(31)

式中pi为第i次车辆轴重，Ni为pi的荷载数循环数，Ntotal为总的监测车辆轮轴数量。

由于车辆荷载的轴重为变幅荷载，且轴重的概率分布据有多峰特征。对于超载率较小的轮轴(RO L<2),细节点的疲劳裂纹扩展往往不会发生迟滞效应。故本文仅讨论轮轴超载率大于2的车辆轮轴对细节疲劳寿命的影响。由WIM系统监测数据可知，2014年至2016年南溪长江大桥单一行车道经历货车的轮轴数量的数量级为100万。在运营3年间，有2次车辆轮轴超载率大于2。图10 为考虑与不考虑车辆轮轴超载率作用下细节点在2014年至2016年疲劳裂纹扩展曲线。两种情况下，裂纹深度达到0.022 mm时所用的时间分别为30.02月和35.91月。考虑车辆超载迟滞效应的计算结果与传统计算结果相差19.6%，需考虑超载迟滞效应的修正系数ξO L。南溪长江大桥焊接细点的超载迟滞效应修正系数ξO L为0.804。

图10 考虑与不考虑车辆轮轴超载细节疲劳裂纹扩展曲线Fig.10 Illustration of crack propagation with and without considering overloads for Detail

5 结 论

本文从随机性的角度详细讨论了车辆作用下OSD焊接细节的疲劳扩展。得到以下结论。

(1) 日交通流密度在不同时间区段有着显著差异，车辆荷载的随机过程不能用单一的数学随机过程模型来描述。非齐次复合Possion过程模型与车辆实际运营状态拟合度高。

(2) 推导了应力时间序列-疲劳损伤微分方程，该方程可以描述车辆疲劳效应与材料疲劳抗力之间的耦合关系。

(3) 车载次序和超载对疲劳裂纹的扩展速率的影响不可忽略。相同车辆类型和数量的车辆，当重车排序靠前时能够促使裂纹快速扩展。在交通荷载统计数据中，需要对超载车辆轴重的超载率和数量进行统计，南溪长江大桥焊接细点的超载迟滞效应修正系数为0.804。