静止无功发生器谐波模型及其对谐振影响分析

刘可，王轩，王杨，王昕，杨放南，李剑武，刘冬平，郭财，张启晟，陈海盟

(1. 国网青海省电力公司电力科学研究院，青海 西宁 810008；2. 四川大学 电气工程学院，四川 成都 610065；3. 深圳市中电电力技术股份有限公司，广东 深圳 518000；4. 国网青海省电力公司，青海 西宁 810008；5. 国网青海省电力公司检修公司，青海 西宁 810008)

0 引言

在能源短缺和气候变化的背景下，大量光伏接入现代电力系统中以实现能源转型和“碳中和”的目标[1]，静止无功发生器（static var generator，SVG）作为新一代的无功补偿装置被大量应用于光伏场站出口侧，用以调节电网功率因数、抑制公共连结点（point of common coupling，PCC）不平衡电压和提升低压穿越能力[2-3]。然而投运SVG后光伏场站依然存在许多电能质量问题，其中谐波谐振问题最为显著[4-5]。与传统电力系统中存在的谐振问题不同，光伏场站中的谐波谐振问题涉及光伏机组并网电压源换流器（voltage source converter，VSC）与SVG的交互作用[6]，因此详细分析VSC与SVG对谐波谐振问题的影响至关重要。

针对光伏场站的谐波谐振问题已经有大量研究，然而多数研究仅考虑了光伏机组的作用而忽略了SVG的影响[7]。SVG和光伏机组并网VSC的拓扑结构和工作原理在本质上相似，主要区别在于指令电流的生成方式。因此，用于VSC的分析方法也可以进一步用于SVG的分析。阻抗分析法是一种广泛应用的谐振分析方法[8]，其不依赖于系统参数的完整性，而是通过分析电力电子装置对小信号扰动的响应获得，在系统内部参数未知时还可以基于测量端口特性进行分析[9]。根据阻抗建模坐标系的差异，阻抗模型主要分为dq阻抗模型[10]以及序阻抗模型[11]。然而，上述2种模型在谐波谐振分析过程中往往忽略了VSC的频率耦合特性。例如，文献[12]忽略了dq轴阻抗中VSC的外环控制，进而忽略了谐波耦合效应；文献[13]中的序阻抗模型仅揭示了单频谐波响应，仍未考虑频率耦合效应。

由于锁相环(phase locked loop，PLL)[14]、电流不对称控制[15]和直流电容动态效应[16]等非线性环节的影响，VSC会产生频率耦合效应，这种现象已在次/超同步振荡中得到广泛研究[17]。然而，当涉及稳态谐波分析时，不同频率之间的耦合大多被忽略或仅被定性分析。文献[18]建立了具有有功/无功功率控制的VSC的阻抗矩阵模型，但其在谐波潮流研究中省略了耦合阻抗。文献[19]对下垂控制的分布式发电系统建立了VSC的耦合阻抗模型，并得出改变下垂系数对并网稳定性产生影响的结论，但仅仅限于50 Hz频段附近，忽略了其他频段的耦合效应。实际上，不同的控制方案可能导致谐波之间不同程度的耦合，SVG特殊的控制结构使得其阻抗模型无法与光伏机组阻抗模型完全相同。目前针对SVG的频率响应特性研究很少，有必要对SVG建立完整的阻抗模型并进一步分析其对谐波谐振的影响。

针对上述问题，本文通过分析SVG对多频谐波扰动的响应，建立一种新型谐波耦合阻抗矩阵模型。在该模型中，频率耦合以解析阻抗形式给出，因此可更好地应用于谐波谐振分析。所提模型经实际光伏场站验证，结果表明SVG较光伏机组具有更明显的频率耦合特性，忽略频率耦合对谐振分析结果具有较大影响。

1 SVG的工作原理

SVG接入电力系统主接线图如图1所示，为了提高系统PCC电压在扰动后的动态恢复能力，SVG通过串联LC无源滤波器并入系统。图中：Us(a,b,c)、Is (a,b,c)和Zs分别为系统侧电压、电流和阻抗；Ug(a,b,c)、Ig(a,b,c)分别为公共连接点（point of common coupling, PCC）电压和电流；Udc为SVG的直流侧电压；Il(a,b,c)为负荷电流。

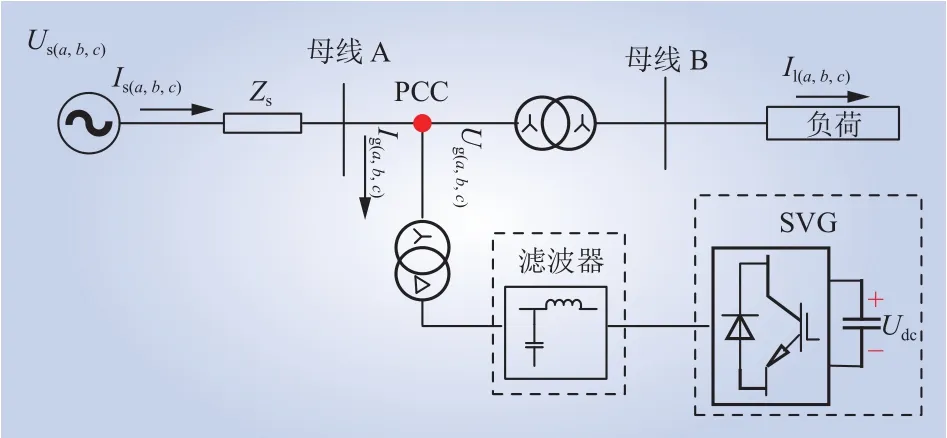
图1 SVG系统主接线Fig. 1 Main electrical connection diagram of SVG system

图2为SVG的控制方案，其采用由外环控制和内环控制组成的双环控制方案。外环控制用于维持直流侧电压Udc和交流侧电压Uac的稳定，并为内环控制提供参考信号。内环控制进一步输出调制信号，该调制信号被馈送到脉宽调制开关(pulse width modulation，PWM)中以实现开关功能，并实现对SVG输出电压Uc的最终控制。SVG的控制通常设计在同步旋转坐标(dq轴)中，控制回路的调节器通常采用PI调节以获得无静态误差的跟踪能力。

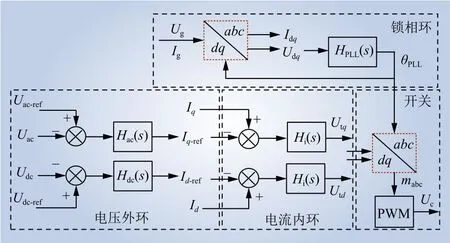
图2 SVG控制策略Fig. 2 Control strategy of SVG

虽然SVG内环控制与传统VSC的内环基本一致，但是它们的外环控制有较大差异，由于电力电子装置的控制方案严重影响其频率响应特性，因此有必要进一步分析SVG的阻抗模型以获得其频率响应。

2 SVG谐波模型推导

通过分析SVG对交流侧谐波扰动的频率响应，可以建立用于谐波谐振分析的SVG谐波模型。考虑到频率耦合效应，需要假设系统存在多频率的谐波扰动。SVG的谐波建模思路如图3所示，将在后续分析中进一步解释图中相关变量的物理意义。该图显示了SVG谐波响应的闭环分析路径，解释了谐波扰动在SVG内部的传递流程，以及影响SVG交流侧谐波电压电流的机理。具体而言，交流侧的谐波扰动将受控制回路影响，进而导致调制信号和开关功能包含谐波成分，即影响SVG交流侧的输出电压。另一方面，直流侧也会因开关过程而受到交流侧谐波的影响。因此，通过解析推导图3中的谐波响应，能够得到PCC处的谐波电压和电流的相关方程，从而解出SVG的完整谐波模型。

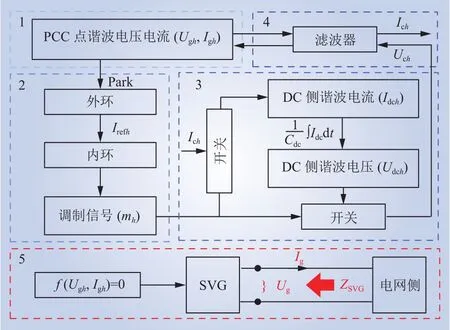
图3 SVG的谐波建模思路Fig. 3 Harmonic modeling of SVG

2.1 PCC多频谐波扰动

包含多频谐波的PCC处a相电压和电流可表示为

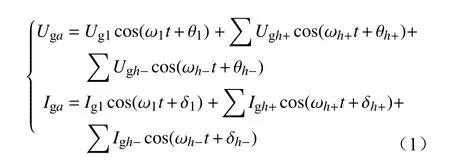
式中：下标“1”表示基频；下标“a”表示a相；下标“h+”和“h-”分别表示正序h次谐波和负序h次谐波；ω为角频率；θ、δ分别是相应的电压和电流相角。b相和c相的电压和电流的相角分别与Uga、Iga相差 ∓ 2/3 π。值得注意的是，图1所示SVG出口侧升压变连接方式为YD1型，零序谐波无法流通，因此式（1）未考虑零序谐波。SVG的控制过程在dq轴中执行，因此有必要将初始abc变量转换到dq轴，即

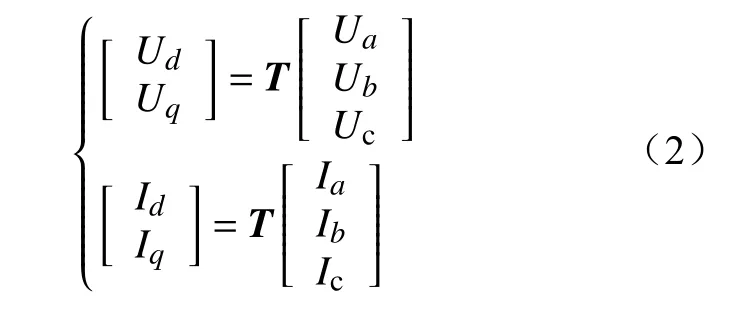
式中：T是派克变换矩阵。式（1）（2）为了简化分析忽略了负序基频分量，这是因为正常情况下系统负序基频分量较小。如果系统含有负序基频分量，需稍作修改，但方法依然适用。

2.2 控制回路推导

当采用图2所示的控制方案时，SVG外环控制的输入包含交流电压Uac，其大小为

当式（2）代入式（3）时，对于基波来说结果是线性的，但对于谐波信号来说Uac是非线性的，采用泰勒级数展开法对其进行线性化，结果如式（4）所示。

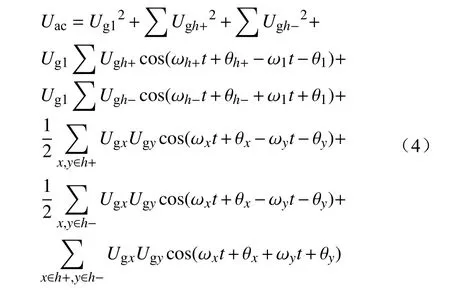
式中：下标“x”和“y”分别表示x次谐波与y次谐波。

式（4）体现了多频谐波在交流电压外环的响应，由于谐波与谐波之间的交互相比于基波与谐波之间的交互小得多，因此式（4）中频率为x次和y次的谐波之间的相互作用可以忽略。上述线性化的误差如图4所示。可以看出，即使单次谐波电压畸变率达到了20%，线性化的误差也仅为5%。而在正常运行情况条件下，电网谐波电压畸变率远远小于20%，这意味着本文使用的线性化方法有着良好的工程适用性。

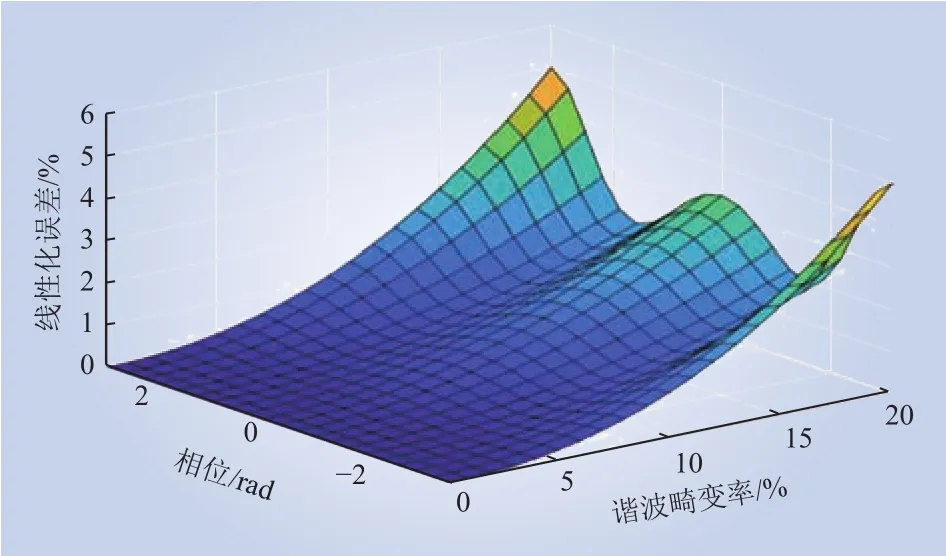
图4 不同谐波电压下的线性化误差Fig. 4 Linearization error under differentharmonic voltages

2.3 交直流侧谐波交互

2.4 谐波模型完整表达式

由所建立模型可知

（1） SVG可以表示为谐波耦合阻抗矩阵。

（2） 从式（7）可以看出，交流电压外环和直流电压外环具有不对称性，所以外部控制回路是SVG频率耦合的主要原因。

（3） 频率耦合效应表现在负序和正序谐波之间，它们的频率相差两倍基频。这意味着正序谐波h+导致负序谐波h+-2，负序谐波h-导致耦合的正序谐波h-+2。

（4） 从式（10）可以看出，直流母线动态过程也与频率耦合有关，直流电容的存在使得直流电压包含谐波分量，促使SVG输出电压响应出新的耦合分量并偏离了调制信号；此外，直流电压还会影响外环控制的对称性，进一步影响调制信号的谐波分量，但影响较小。

3 仿真验证

利用Matlab/Simulink simscape电气仿真软件，在图5所示的实际光伏集成系统中验证本文提出的SVG谐波耦合阻抗矩阵。该系统包含一个12 MW的光伏发电厂，并连接一个±3 MV·A SVG来满足光伏发电厂的无功需求。其中光伏接口逆变器控制策略设计为有功/无功功率控制；SVG控制策略设计为交流和直流电压控制。SVG和光伏参数分别如表1和表2所示。

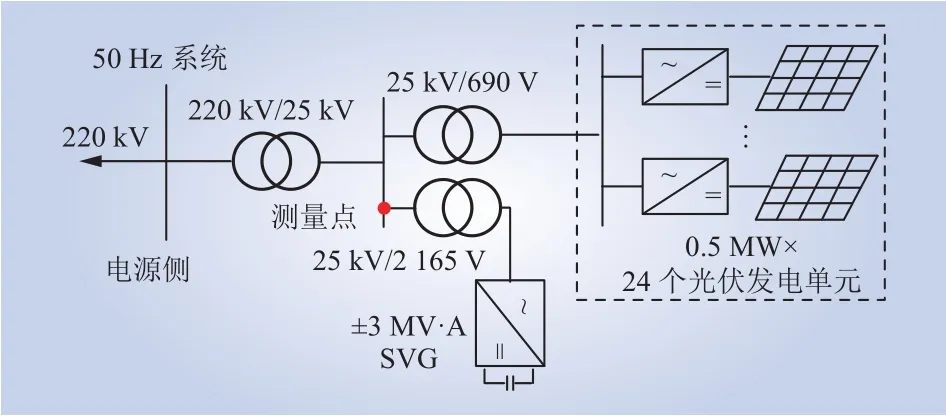
图5 用于仿真验证的光伏系统Fig. 5 PV system for simulation verification

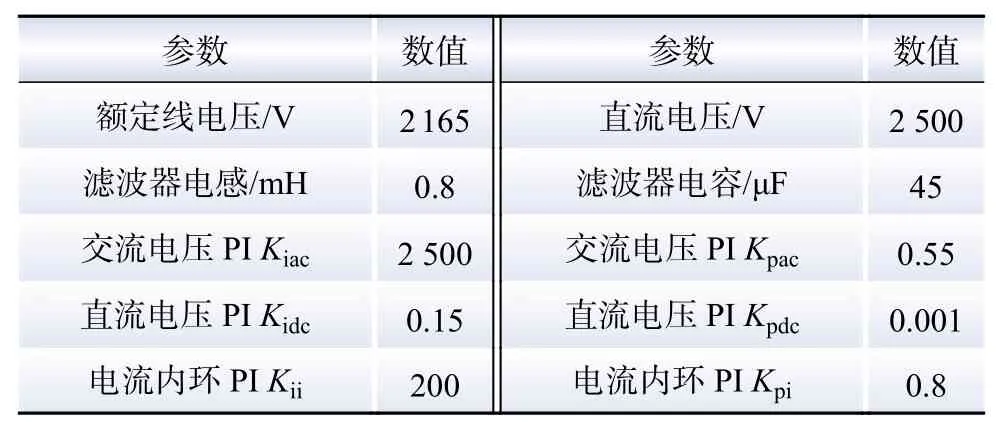
表1 SVG的主要参数Table 1 Main parameters of SVG

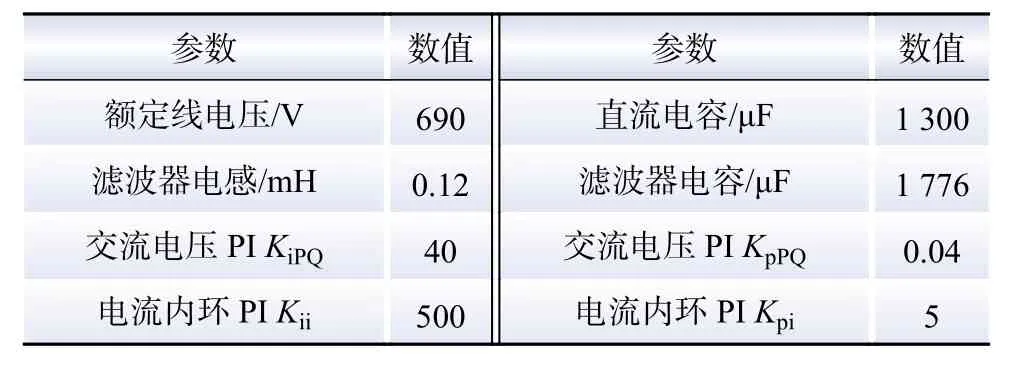
表2 光伏主要参数Table 2 Main parameters of PV

3.1 耦合阻抗模型的验证

首先进行SVG谐波耦合阻抗模型的验证。在系统侧添加频率相差两倍基频的正序谐波电压和负序谐波电压，通过测量SVG交流侧的谐波电压和电流，可以使用式（18）求解谐波阻抗矩阵。

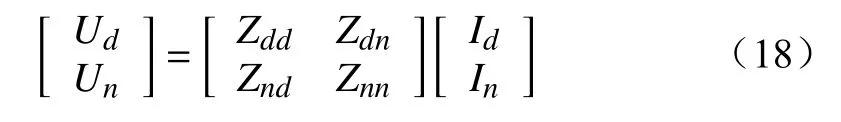
式（18）中d和n满足式（13）中的关系。阻抗矩阵中有4个未知数，因此需要添加2组线性无关的谐波扰动。将仿真获得的结果与所提出的模型获得的结果进行比较，如图6所示。可以看出，所提出的谐波耦合阻抗矩阵与时域仿真结果有较高的相似性，验证了所提模型的正确性。

3.2 光伏场站谐波谐振分析

上述分析表明，频率耦合存在于SVG的交流侧，这种频率耦合对于谐波谐振的影响将在本小节进行研究。通常可以通过频率扫描方法检测谐波谐振。该方法将特定谐波频率下的电流注入设置为0.01～0.1 p.u.以获得频率结果。但是，由于SVG的频率耦合明显，这种单输入单输出扫频方法很难使用。本文定义谐波放大系数（HAR）RHA作为谐波谐振指标[20]。

用户可以定义RHA来检测系统是否发生谐振，例如，如果RHA大于1.2，则定义SVG或光伏接口逆变器的连接引起谐波谐振；否则，就未引起谐波谐振。所研究系统的HAR可以表示为交流侧电压注入和阻抗矩阵的函数。

为了显示频率耦合对谐波谐振分析的影响，在电网侧电压中加入满足式（13）关系的2个谐波，低阶谐波设置为10%，高阶谐波设置为5%。在图7中比较了考虑和不考虑频率耦合效应的情况下算得的RHA，图8为系统PCC电压电流。可以看出，当不包括频率耦合效应时，RHA最大达到了1.346，即系统在第11次谐波处存在谐振。然而，考虑频率耦合计算的RHA表明系统不存在谐波谐振。计算得出的RHA与仿真结果也相匹配。上述结果表明，如果忽略频率耦合效应，谐波谐振分析结果可能产生较大的误差。

图7 光伏系统的HARFig. 7 HAR of PV system

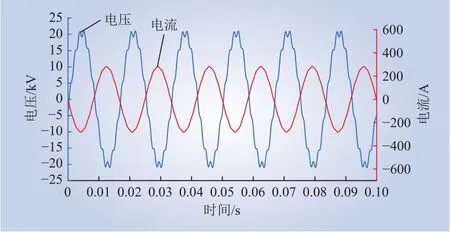
图8 PCC处电压电流Fig. 8 Measured voltage and current of PCC

3.3 直流电容的动态影响

当系统发生暂态过程时，直流母线电容电压会有较大的波动，忽略直流电容可能会使得SVG阻抗模型的建立产生误差。但是本文主要关注稳态谐波下SVG的响应特性，因此暂态扰动不予考虑。

稳态场景下，直流母线动态过程对SVG阻抗的影响如图9所示。从图9可以看出，当直流电压源被不同大小的电容器代替时，SVG阻抗Zdd的变化有限，表明直流母线动态过程对谐波响应的影响可以忽略不计。Zdn、Znd和Znn的结果是相似的。原因是当电容较大时（实际情况多如此），式（10）引入的交流和直流侧之间的谐波耦合和电容引起的谐波电压变得非常小。此时，可以认为调制比中的谐波分量与控制电路中的谐波分量完全相同。

图9 不同直流电容下Zdd的大小Fig. 9Zddunder different DC capacitors

4 结论

基于多频谐波响应思想，本文建立了计及频率耦合特性的SVG谐波耦合阻抗模型。该模型可以准确地表示各种谐波畸变下SVG的频率响应，并有效揭示频率耦合效应的机理。分析结果表明，电压控制模式的SVG在中低频段的耦合较强，因此对于光伏场站的谐振分析来说，有必要考虑SVG接入后的影响。此外，直流母线动态过程对于SVG的谐波响应影响有限，因此在大多数工况下可以忽略不计。

值得注意的是，虽然本文推导的解析公式较为复杂，但除外环控制外，并网逆变器的控制结构差异较小，因此可以方便地推导出不同控制方案的谐波阻抗模型，即这种建模思路具有普适性。