计及分时电价的5G基站光储系统容量优化配置方法

韩子颜，王守相，赵倩宇，郑志杰

(1. 智能电网教育部重点实验室（天津大学），天津 300072；2. 电力系统仿真控制天津市重点实验室（天津大学），天津 300072；3. 国网山东省电力公司经济技术研究院，山东 济南 250021)

0 引言

随着新型基础设施建设概念的提出，排在“新基建”七大产业中第一位的5G基站建设得到了大力发展[1]。2019年11月，5G通信开始商用，对5G基站建设的投入不断加大。截至2021年9月，全国已累计开通超过115.9万个5G基站，终端连接数达4.5亿[2]，预计到2025年中国5G基站数量将达800万个[3-4]。

数量庞大的5G基站可以保障5G网络覆盖的有效性，也会增加通信运营商的用电量。目前主要运营的5G基站主设备空载功耗约为2.3 kW，单站满载功耗约为3.8 kW，远超过4 G基站的功耗[5-6]。另一方面，由于5G基站主要部署在高频段，单站覆盖范围变小，平均覆盖范围为450 m左右，而4 G基站的平均覆盖范围为1 500 m左右[7-8]。为了达到同样的通信覆盖效果，5G基站的建设数量也将大大超过4 G基站。预计到2025年，5G基站总用电量将近2 000亿kW·h/年，占全社会用电量的2.0%[9]。因此，通信运营商能否找到有效降低基站耗电量的办法将影响到未来5G通信的普及。

现阶段对于如何减少5G基站的用电成本已展开了诸多研究。文献[10]考虑在不同的通信运营商之间，通过无线负载共享和能源互动使轻负载的基站进入休眠模式，以此来节省能源成本。文献[11]提出了在不同基站间可以分别通过能源合作、通信合作以及能源与通信联合合作的方式，来降低蜂窝网络的能源成本。文献[12]提出了一种设置基础覆盖4 G小区门限，建立邻区忙时唤醒机制的5G智能节能方法，结果证明在实验区域内取得了良好的效果。

与传统电网相比，能源互联网系统允许组件之间能量的双向流动，这推动了5G基站与电网互动理念的发展[13-14]。在能源互联网系统中，为5G基站配置分布式电源和储能装置，未来将成为通信基站能耗高和用电成本大的一种潜在解决方案。通过对配有分布式电源和储能的基站进行用电调度，让通信运营商参与电网需求响应，可以减少用电支出和碳排放。

基于此背景，本文开展了基于光伏发电和储能的5G基站光储系统容量优化配置方法研究，利用光伏发电解决5G基站用电成本大的问题，通过配置储能对光伏出力和峰谷电价差进行合理利用，进一步降低5G基站运行成本。

1 基站能耗模型

基站即公用移动通信基站，是移动设备接入互联网的接口设备。从广义上，基站分为宏基站和小基站2种。根据覆盖范围大小，小基站又可以分为微基站、皮基站和飞基站[14]。相对于宏基站能耗来说，小基站的能耗较小[15]，仅为宏基站能耗的1/200～1/8[16]。本文主要针对能耗较高的5G宏基站进行相关研究，因此，下文中所提到的5G基站均为5G宏基站。

基站主设备的能耗可以分为静态能耗和动态能耗两部分[17]。其中，静态能耗与接入用户无关，是基站维持正常运行的基本能耗；动态能耗是指基站能耗随通信数据量变化的部分，动态能耗与通信数据量成正比例关系[18]。基站主设备的能耗表达式为

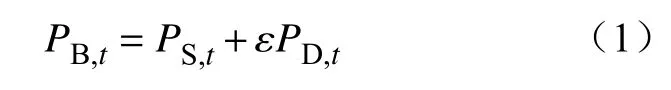
式中：PB,t为基站t时刻的能耗；PS,t为基站t时刻的静态能耗；ε为基站的能耗效率系数；PD,t为基站t时刻的动态能耗。

由于设备硬件的限制，PD,t的取值为

式中：γ为反映通信数据量的系数；PD,max为基站的最大动态能耗。

2 基站光储系统数学模型

2.1 目标函数

2.2 约束条件

3 模型求解

粒子群优化（particle swarm optimization, PSO）算法是基于种群搜索的自适应进化计算技术。作为一种重要的优化工具，PSO算法已经成功地应用于函数优化、神经网络训练等领域[21]。

PSO算法不能保证以概率1搜索到全局最优解，收敛速度一般[22]。为了解决上述问题，文献[23]从量子力学的角度考察粒子个体与群体的进化模式，提出了收敛速度更快且具有全局收敛性的量子粒子群优化（quantum-behaved particle swarm optimization, QPSO）算法。与PSO算法相比，QPSO算法中的粒子只带有位置信息，算法的控制参数相对更少，具有全局寻优能力强和计算耗时短的优点[24-25]。

当粒子在搜索空间中移动时，存在着一个以局部吸引点为中心的δ势能吸引着粒子，这正是粒子能够保持聚集性的原因[26]。由于在δ势能的吸引下，粒子可以在整个可行域的范围内按照不确定的搜索轨迹进行搜索，使得QPSO算法具有全局收敛性。

在第k次迭代时，粒子i在第d维的势阱为

式中：pbestid为粒子i的个体最优位置；gbestd为群体的全局最优位置；φ(k)为服从(0, 1)上均匀分布的随机数。

粒子的位置更新方程为

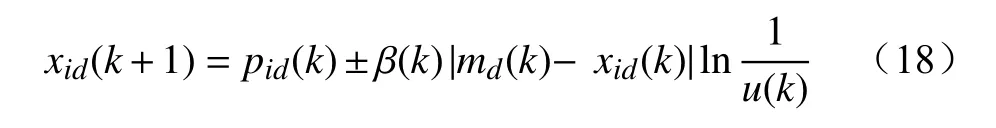
式中：β(k)和u(k)均为服从(0, 1)上均匀分布的随机数，β(k)前的符号取决于u(k)的大小，当u(k)＞0.5时，β(k)前的符号为负，反之则为正；md(k)为第k代第d维的平均最优位置，即所有粒子自身最优位置的中心，其具体计算式为

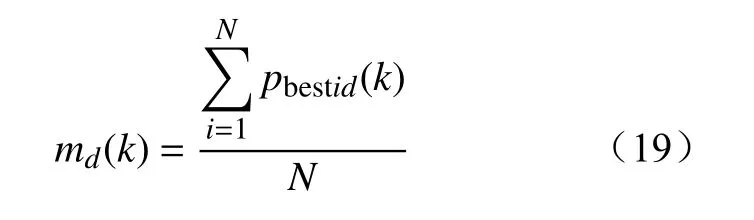
式中：N为粒子群体大小。

对于本文的优化问题，采用QPSO算法进行求解，粒子群体大小N为5 889，维数d为25，目标函数为适应度函数。在满足约束条件的情况下，求得5G基站光储系统的综合成本费用最小值，并可以确定光伏和储能的最佳接入容量。求解流程如图1所示。

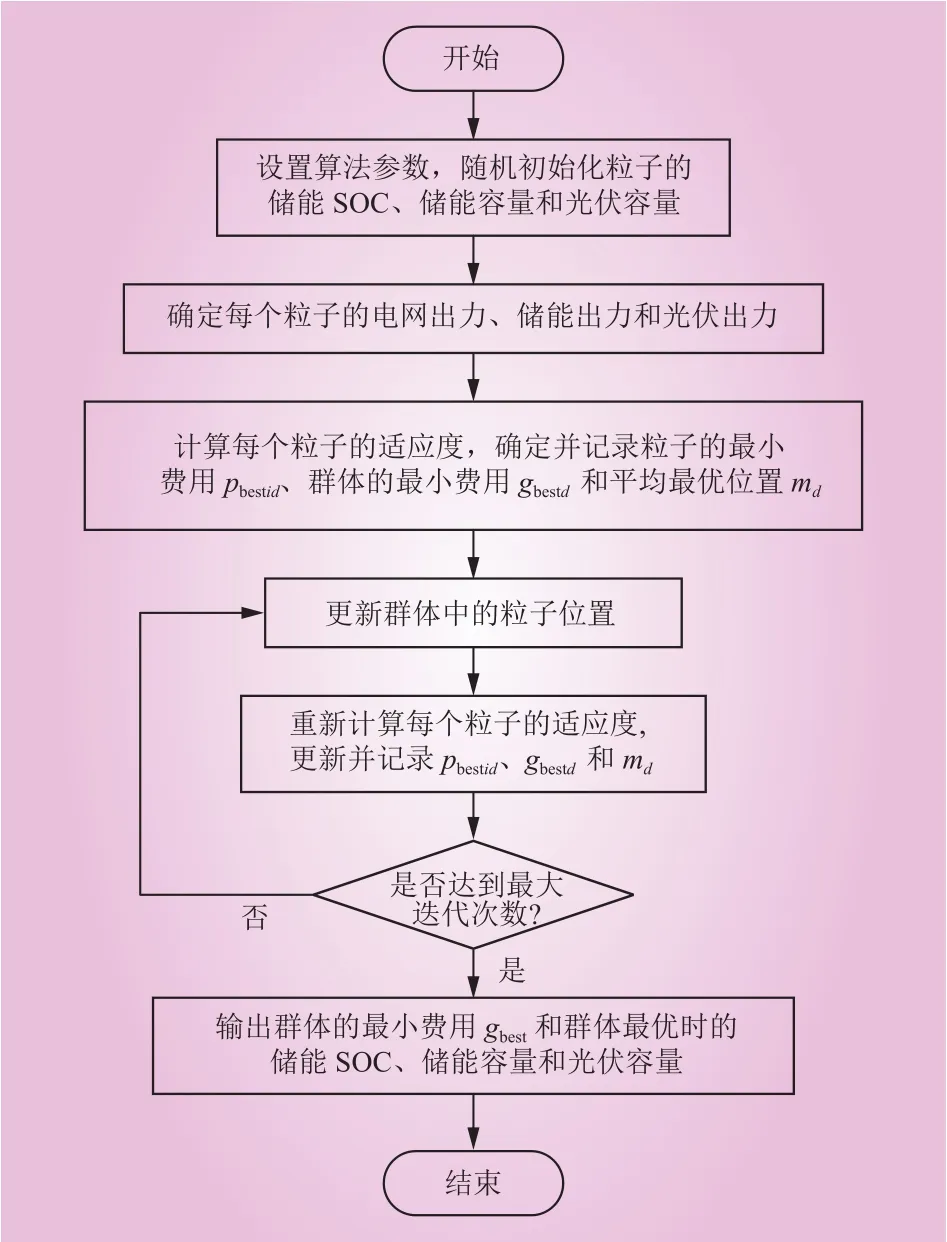
图1 QPSO 算法流程Fig. 1 Flow chart of QPSO algorithm

4 算例分析

4.1 数据资料

选取天津市某5G基站为例，已知该基站站址具备建设光伏发电和储能的条件。

该基站的静态能耗为2.3 kW，基站的能耗效率系数为2.857 1[27]，基站的最大动态能耗为550 W。通信数据量系数的选取与流量高低有关，在02:00—07:00时段为[0.5, 0.75]间的随机数，在00:00—02:00、08:00—24:00时段为[0.75, 1]间的随机数。为保证算例分析不受通信数据量系数的影响，数值大小在每个场景中保持不变。

这里做以下假定：光伏的最大允许安装容量为15 kW，光伏发电的建设成本为3 735元/kW，单个光伏组件最大发电功率为400 W，回收年限为15年，单位输出功率的维护费用为0.21元/kW。储能的最大允许安装容量为15 kW·h，单位容量安装投资费用为1 000元/(kW·h)，单位容量年运行维护费用为100元/(kW·h)，平均每天的衰减率取0.04%，回收年限为8年，荷电状态的上下限分别为0.95、0.3，系统贴现率取8%。

为了分析不同电价对结果的影响，设计了具有相同背景和参数设置的3个场景，区别如下。

（1）场景1：基站光储系统一天各个时段向电网的购售电价如表1所示。

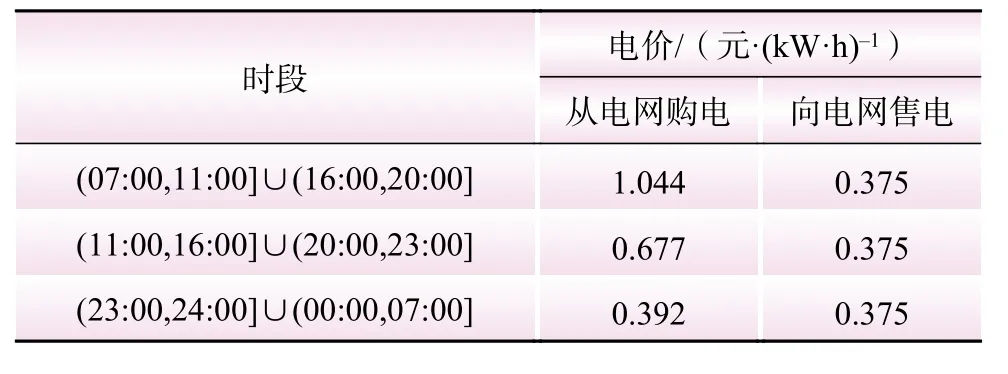
表1 场景1 的分时电价Table 1 Time-of-use electricity price of scenario 1

（2）场景2：将基站光储系统向电网购电电价的峰谷价差调整为3∶1，具体数值如表2所示。

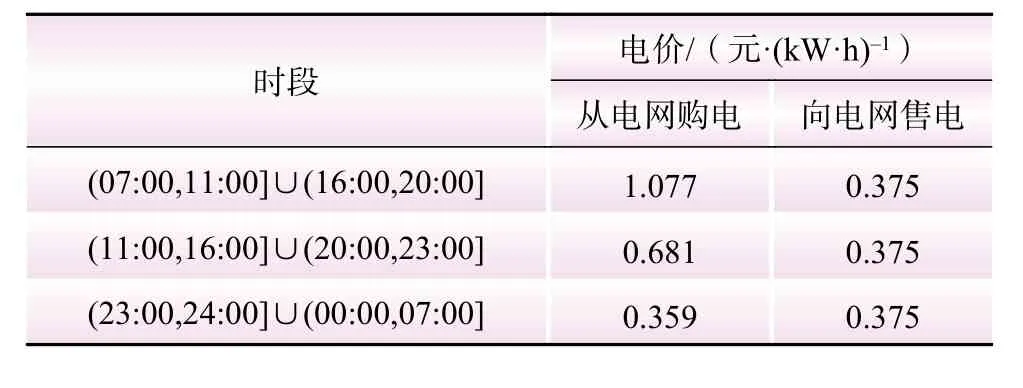
表2 场景2 的分时电价Table 2 Time-of-use electricity price of scenario 2

（3）场景3：将基站光储系统向电网购电电价的峰谷价差调整为4∶1，具体数值如表3所示。

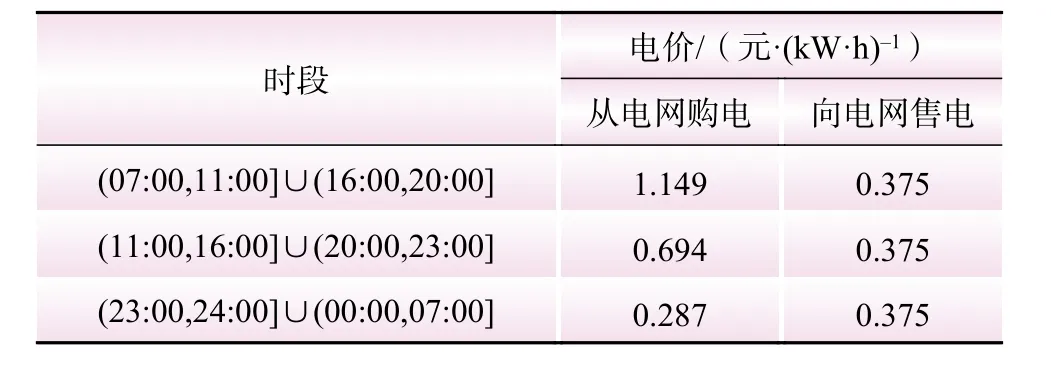
表3 场景3 的分时电价Table 3 Time-of-use electricity price of scenario 3

4.2 结果分析

3个场景初始情况（未考虑光伏发电和储能建设时）的基站运行成本与程序运行结果中基站综合成本的对比如表4所示。由表4可以看出，随着电价峰谷差的扩大，未考虑光伏和储能建设时基站的运行成本略有提高，考虑配置光伏和储能后基站的综合成本下降。这说明合理增大分时电价的峰谷价差可以提高5G基站光储系统的经济性。

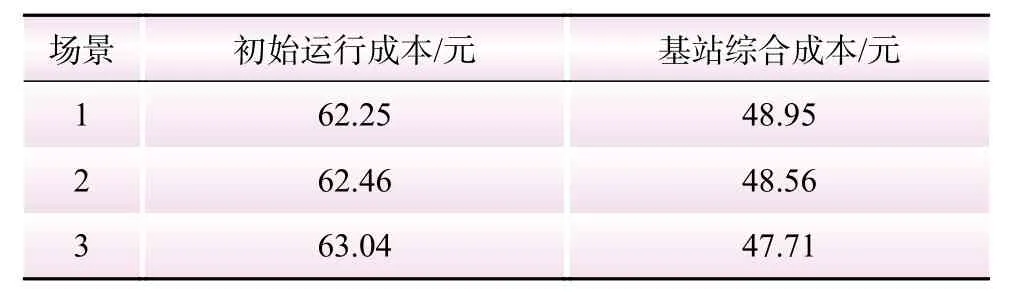
表4 成本对比Table 4 The cost comparison

场景1的程序运行结果中光伏容量为6.8 kW，储能容量为0；场景2的程序运行结果中光伏容量为6.8 kW，储能容量为0；场景3的程序运行结果中光伏容量为10.4 kW，储能容量为0。与场景1、场景2相比，场景3的光伏容量较大，说明配置光伏的容量受分时电价的峰谷价差影响。在一定程度上，峰谷价差越大，可建设光伏的容量越大。3个场景中，储能容量均为0，说明在3个场景的分时电价条件下，储能的投资和运行维护成本较高，引入储能将无法收回成本。

为了探究系统经济效益与储能成本的关系，假设储能单位容量安装投资费用逐渐下降，其余数据均保持不变，分析3种场景下光伏、储能容量和系统综合成本随储能成本变化，结果分别如图2、图3、图4所示。

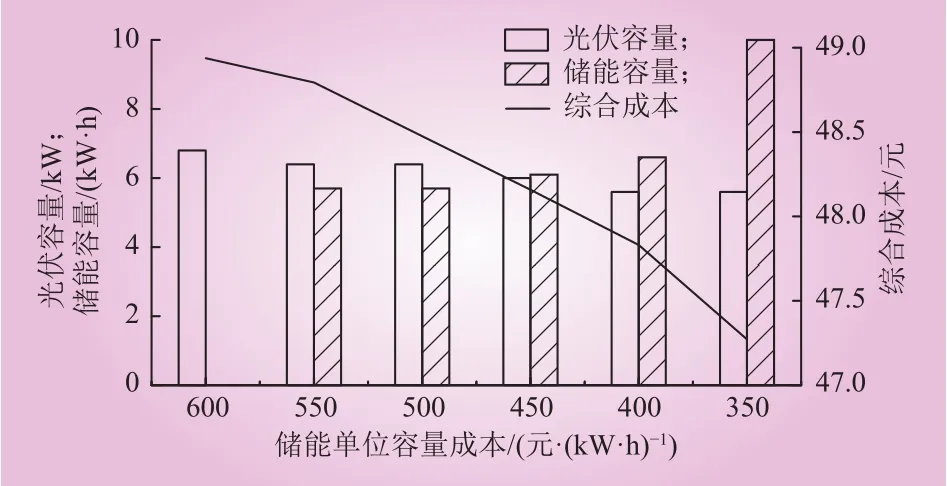
图2 场景1光伏、储能容量和综合成本与储能成本的关系Fig. 2 The relationship between photovoltaic, energy storage capacity and comprehensive cost and energy storage unit capacity cost in scenario 1

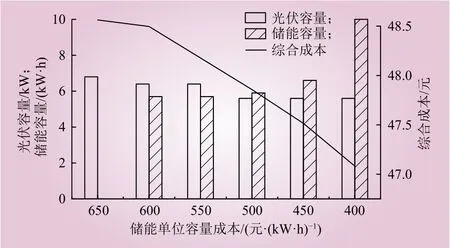
图3 场景2光伏、储能容量和综合成本与储能成本的关系Fig. 3 The relationship between photovoltaic, energy storage capacity and comprehensive cost and energy storage unit capacity cost in scenario 2

图4 场景3光伏、储能容量和综合成本与储能成本的关系Fig. 4 The relationship between photovoltaic, energy storage capacity and comprehensive cost and energy storage unit capacity cost in scenario 3

由图2、图3、图4可以看出，储能成本降低，可配置的储能容量随之增加，5G基站光储系统的综合成本减少。在场景1分时电价的条件下，储能成本下降到571元/(kW·h)时，储能开始投入建设；在场景2分时电价的条件下，储能成本下降到608元/(kW·h)时，储能开始投入建设；在场景3分时电价的条件下，储能成本下降到704元/(kW·h)时，储能开始投入建设。说明在分时电价固定的情况下只有储能成本下降到超过一定阈值时配置储能才具备经济性。当电价峰谷差增大，储能在单位容量成本较高时可以投入建设。这说明随着分时电价峰谷价差的增大，对储能成本阈值的要求会相应降低，储能所能带来的经济效益增加，5G基站光储系统对于储能的接纳能力提高。

随着储能成本降低，储能开始建设，储能容量增大，但光伏容量会减小。其主要原因是在储能容量为0时，为了减小系统的综合成本，尽可能地使光伏可以满足电价高峰时段基站能耗的供给。当系统开始配置储能后，由于储能可以将正午多余的光伏发电量转移到傍晚电价高峰时段，光伏容量可以适当减小。当光伏容量为5.6 kW时，储能成本继续降低，光伏容量将不再变化，即光伏容量小于5.6 kW时，配置光伏不具备经济性。

以场景1中储能单位容量成本为450元/(kW·h)时为例，一天时间内系统每小时功率变化情况如图5所示。

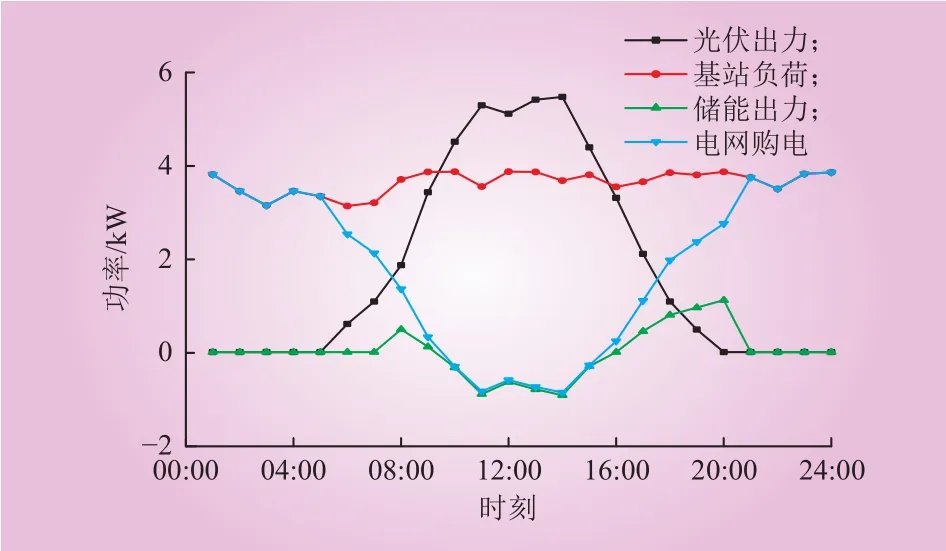
图5 每小时功率情况曲线Fig. 5 Power curve of each hour

由图5可以看出，00:00—05:00和23:00—24:00时段光伏发电出力为0，电网购电量等于基站能耗；05:00—07:00时段光伏设备开始发电，光伏出力小于基站能耗，系统从电网购电，电网购电量等于基站能耗减去光伏出力；07:00—09:00时段光伏出力小于基站能耗，系统仍从电网购电，此时处于电价高峰时段，储能放电来减少一定的购电成本，电网购电量等于基站能耗减去光伏出力和储能放电量之和；09:00—16:00时段光伏出力大于基站能耗，储能充电，光伏在满足基站能耗和储能充电量后的多余出力向电网售电；16:00—19:00时段电价处于高峰时段，光伏出力小于基站能耗，储能放电为基站提供部分电量，电网购电量等于基站能耗减去光伏出力与储能放电量之和；19:00—20:00时段光伏发电出力为0，电价仍处于高峰时段，储能放电，但放电量小于基站能耗，系统需从电网购电；20:00—23:00时段光伏发电出力为0，分时电价处于平时段，储能不工作，电网购电量等于基站能耗。

储能利用白天光伏出力有剩余时进行充电，在其余高峰电价时段放电，减少系统的购电费用。这是由于在场景1的分时电价条件下，5G基站光储系统上网电价低于从电网购电的电价，为使系统费用最小，光伏的盈余功率优先选择给储能充电，并且为实现储能经济效益最大化，储能优先在电价高峰时段放电。

5 结论

本文为解决现阶段5G基站耗电量大、通信运营商成本高的问题，提出了5G基站光储系统的容量优化配置方法，考虑不同分时电价和储能成本对5G基站光储系统经济效益以及光伏、储能配置容量的影响，取得以下结论。

（1）考虑为5G基站配有合理容量的光伏发电和储能，可以降低基站的综合成本，有效缓解现阶段购电费用高的问题。提高分时电价的峰谷价差和降低储能成本，都会增加光储系统所能带来的经济效益。

（2）储能的配置容量受分时电价和储能成本的影响。在固定分时电价的情况下，当储能成本下降至一定阈值时，配置储能才具备经济性。随着峰谷电价差增大，对开始建设储能的阈值要求也会降低。

（3）光伏发电的配置容量受分时电价和储能容量的影响。在一定程度上峰谷价差越大，光伏发电容量越大；储能容量增大，光伏容量逐渐减小，当光伏容量小于某阈值时，配置光伏不具有经济性，因此光伏容量减小至某阈值后将不再减小。

现阶段储能的投资建设成本较高，引入储能可能无法收回成本。因此在后续的研究中可以在保留满足基站应急电能的前提下对5G基站自身配置的冗余储能进行调度，并继续探讨相应的方法。