适用于PET的负载电流前馈控制策略

李帅虎，王婷婷，刘制，彭寒梅，唐坤

(1. 湘潭大学 自动化与电子信息学院，湖南 湘潭 411104；2. 长沙理工大学 电气与信息工程学院，湖南 长沙 410082；3. 资阳石油钢管有限公司，四川 资阳 641300)

0 引言

随着能源互联网的提出和电力电子技术的不断发展，传统的电力变换器在能量配置范围、综合控制能力、电能质量等方面的局限性逐渐显现[1]。电力电子变压器（power electronic transformer,PET）作为一种新型电力变换装置应运而生，受到国内外学者广泛关注。目前，研究最为广泛的PET拓扑为级联型PET[2]，它不仅能够实现电压等级变换和电气隔离，还提供交流侧的无功补偿和谐波治理，并且具有功率控制灵活，易于模块化扩展和可控性较高等优点[3-7]。

在半导体器件耐压水平的限制下，为满足高压大容量的应用场合需要，级联型PET由输入级H桥串联形成的级联H桥（cascaded H-bridge，CHB）与隔离级并联的双有源桥（dual active bridge，DAB）变换器级联组成[8-9]。然而，PET组成模块的增加，使得电力电子变压器对其各子模块控制和端口之间的协调控制面临更多挑战。总体而言，针对PET的研究，不仅须考虑PET内部的电压均衡和功率均衡[10-13]，而且还须考虑高、低压直流母线电压抗扰性能及稳定问题[14-16]。文献[10-11]提出CHB采用电压均衡控制，DAB实现无电流传感器的功率均衡控制，解决了因DAB参数不匹配导致的功率不均衡问题；文献[12-13]将电压均衡与功率均衡控制都集中到DAB上，该策略的优点在于控制算法简单且控制性能优越。上述文献对PET的均衡控制进行了研究，但并未考虑直流电压的动态响应和系统稳定性问题。电力电子变压器在一定的限度内能抑制电压暂降、上升、谐波等电压畸变对用电设备造成的不利影响，保证系统稳定运行[14-15]。然而，PET隔离高、低压侧电能质量干扰的能力有限，由于控制环节的滞后性和电容值限制等原因，负荷波动时容易造成高、低压直流母线电压的大幅度波动[16]。

直流母线电压的波动理论上可以通过增大直流母线电容进行抑制[17]，但该方法不利于增大功率密度和降低成本。文献[18]对各子系统的稳定性进行了分析，从阻抗交互角度研究了基于Z+Z型串级系统阻抗分析的评估方法，提升了系统的整体稳定性。文献[19]通过构建CHB与DAB之间的协调控制，将高、低压直流母线电压控制任务分派至CHB级与DAB级共同承担，以减小CHB与DAB功率响应速度之间的差异，达到减小高压直流母线电压波动的目的。然而，上述研究成果都是通过前级和后级协调匹配，达到抑制高压直流母线电压波动的目的，对如何改善低压直流母线电压的抗扰性能并没有显著作用。为此，前馈控制引起关注。文献[20]提出了一种前馈补偿策略来实现负载变化过程中的瞬态响应，但是控制策略中各子系统均需要独立的电流传感器，相应地增加了系统成本和控制复杂度。文献[21]提出了一种新型的非线性前馈公式和线性前馈公式，实现了DAB变换器在电流模式调制下的瞬态响应，但该方法对电感电流采样非常敏感。

针对上述问题，本文对PET系统CHB级和DAB级的负载电流前馈控制策略进行研究。首先，从经典控制理论的角度深入研究了高、低压直流母线电压波动的机理，分析了负载切换时负载电流对高、低压直流母线电压以及系统稳定性的影响。然后，根据这一特性，本文对传统前馈控制策略做出改进，即针对CHB和DAB提出了仅需一个电流传感器的电流前馈控制策略，从而有效地抑制了高、低压直流母线电压的波动，并从闭环系统根轨迹稳定性详细分析了系统性能。最后，基于Matlab／Simulink搭建了该拓扑的仿真模型，对所提控制策略的性能进行了分析并通过仿真实验来验证该控制策略的可行性和有效性。

1 PET数学建模以及运行原理

级联型PET主电路拓扑结构如图1所示，该拓扑由N个子单元并联而成，其中每个单元由H桥(HB)电路和DAB电路2部分组成。

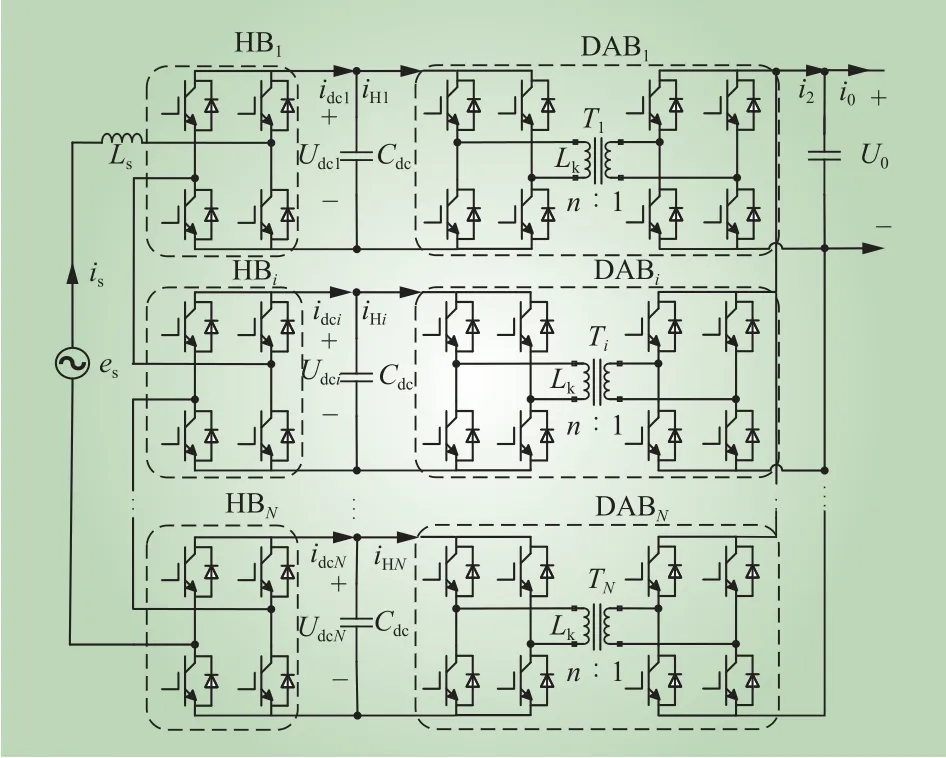
图1 级联式电力电子变压器主电路拓扑Fig. 1 Main circuit topology of cascaded PET

2 负载扰动对PET性能影响的分析

2.1 高压侧直流母线电压波动分析

假设CHB级各子模块参数一致，则各子模块电压及电流均相同，可省略下标i，此时Udci=Udc，idci=idc，iHi=iH，ddi=dd。高压直流母线电压扰动传递框图如图2所示，Gu-p1(s)为CHB电压环PI控制器传递函数，为网侧电流参考信号，Gi-p1(s)为CHB电流环PI控制器传递函数，GD(s)为CHB延迟环节传递函数，GD-p2(s)为DAB电压环PI控制器传递函数。

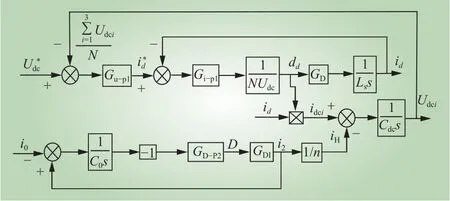
图2 高压直流母线电压扰动传递框图Fig. 2 Voltage disturbance transfer block diagram of high voltage DC bus

CHB电流内环按照典型二型系统设计，具有相对较快的抗干扰恢复能力；而电压外环按照典型二型系统设计，为抑制电压外环噪声信号对系统的影响，电压环带宽通常设计得较低，这使得输出电压变化时恢复时间较长，系统动态性能差。

2.2 低压侧直流母线电压波动分析

隔离级电压控制框图如图3所示，DAB一般采用单电压环控制，使低压直流母线电压跟随其参考信号。

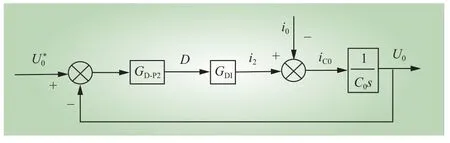
图3 低压直流母线电压控制框图Fig. 3 Voltage control block diagram of low voltage DC bus

3 直流母线电压波动抑制策略及分析

3.1 PET整体的负载电流前馈

为解决负载变化带来的高、低压侧直流母线电压畸变问题，可采用前馈控制来改善系统性能。然而，传统的整流级前馈控制需要测量每个H桥的输出电流，以补偿负载变化对高压直流母线电压的干扰，这将需要大量的电流传感器。同时，高压直流母线输出电流纹波大，易影响CHB输入电流质量。为此，本文提出了一种适用于级联型PET系统的负载电流前馈控制策略，将实现DAB前馈控制的负载电流前馈到CHB，CHB控制器将不再需要额外的电流传感器，其控制框图如图4所示。

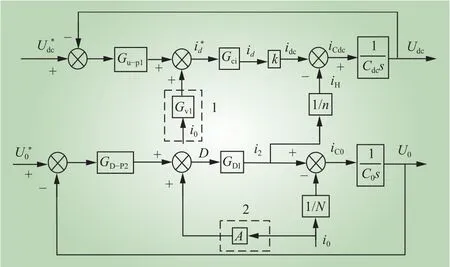
图4 CHB与DAB负载电流前馈控制Fig. 4 Load current feedforward control of CHB and DAB

从图4可见，支路1、2将负载电流前馈至CHB与DAB上。其中，电流内环参考信号上叠加Gv1i0项，Gv1i0为CHB前馈补偿项，Gv1为前馈项系数，而移相比D上叠加Ai0项，Ai0为DAB前馈补偿项，A为移相补偿系数。

关于DAB的前馈控制，通过式（3）可求出一定负载条件下相应的移相补偿系数为

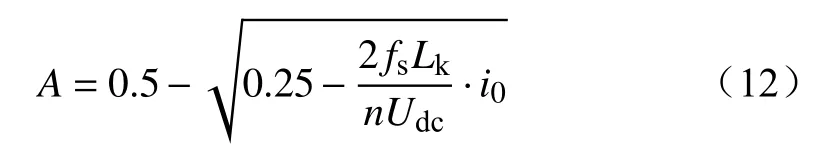
在DAB闭环控制中，前馈控制的A仅和负载电流有关，随着负载变化而调整。

根据图4可绘出前馈控制下低压直流母线电压的扰动框图如图5a)所示，结合式（12）确定的移相补偿系数，可推导出输出电压为

图5 前馈控制下负载电流扰动传递框图Fig. 5 Load current disturbance transfer block diagram under feedforward control

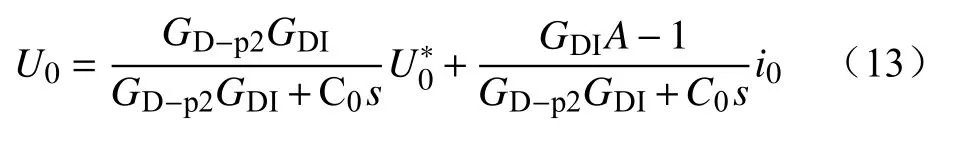
对比式（11）和式（13），可知前馈项产生的移相补偿系数可消除由低压侧电压环PI控制器引起的延迟，从而具有更好的动态响应。

与此同时，前馈控制也可以应用于CHB级。为减小系统成本和降低功耗，根据功率守恒，将隔离级负载电流前馈到输入级的电流内环中，作为整流级前馈控制，前馈控制下的扰动传递框图如图5 b)所示。

由图5可得高压直流母线电压为

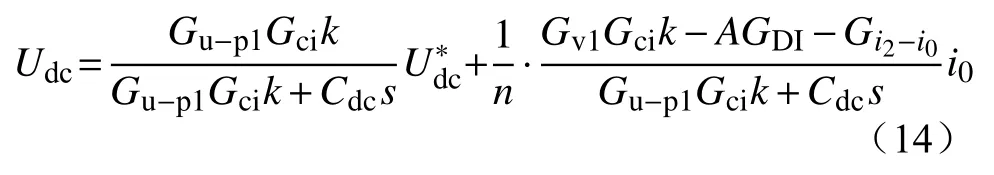
忽略功率损耗，考虑PET整体的输入输出功率守恒，可推导得CHB前馈项系数为

由式（15）产生的前馈系数为CHB主电流，而补偿电流由电压控制回路产生。整流级前馈控制策略将主电流引入电压回路，作为网侧电流参考信号的输入。通过计算产生的主电流可消除电压环带来的延迟，提高系统的可靠性。考虑到电流内环延迟，前馈控制仍需要一定响应时间。

根据文献[22]及式（14）可以看出，只有当Gv1满足式（16）时才能完全消除负载电流对高压直流母线电压的影响。

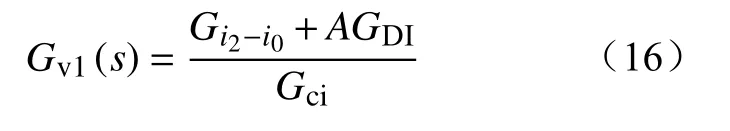
结合式（5）～（7）（12），可得前馈传递函数Gv1(s)的详细表达式为

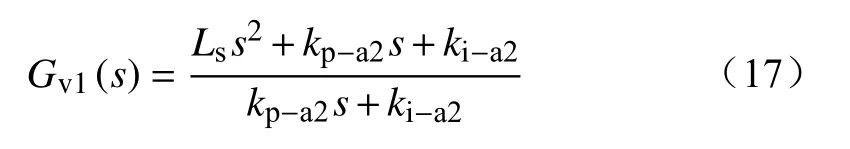
式中：kp-a2和ki-a2分别为CHB电流环的比例和积分系数。基于上述分析，该微分环节的转折频率为ω2=2.84×103rad/s， 故前馈传递函数Gv1(s)可简化为一阶环节。然而，在实际应用中，纯微分环节无法抑制高频噪声信号对系统产生的干扰，可能导致振荡程度加剧，严重时甚至会使系统失稳，所以本文采用积分代替微分。同时，本文前馈电流采用负载电流i0，因此根据功率守恒，在式（17）中还应增加前馈项系数B，得到其最终计算公式为

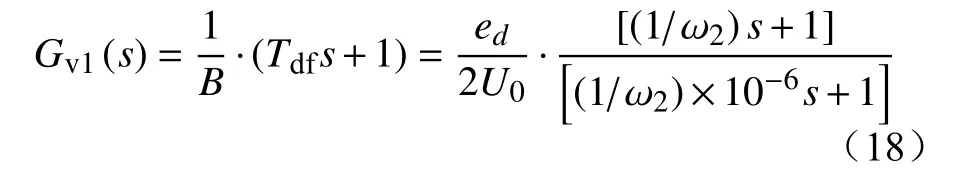
根据图5可绘制高压侧扰动传递函数Udc/i0的伯德图和低压侧扰动传递函数U0/i0的伯德图如图6 a)、图6 b)所示。可以看出，加入前馈控制后，负载电流到高、低压直流母线电压扰动传递函数的幅频特性曲线下移，低频段增益显著减小。这表明加入前馈控制后，电路具有更好的跟踪特性，负载变化对直流母线电压的影响减小[23]。

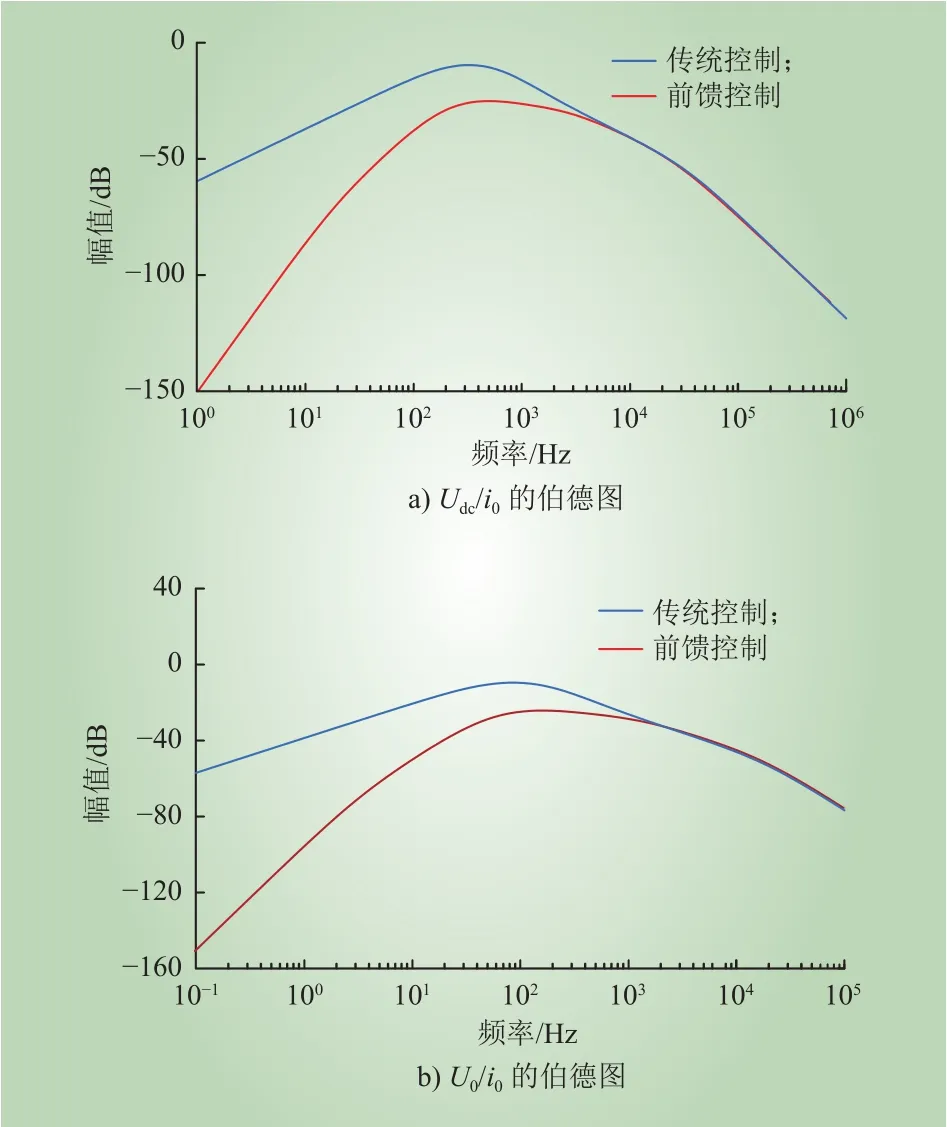
图6 不同控制下的扰动伯德图对比Fig. 6 Comparison of disturbed bode charts under different control conditions

图7 a)、图7 b)分别为传统控制、前馈控制时单位阶跃电流扰动下直流母线电压响应波形对比。从图7可以看出，在传统控制下，高压直流母线电压跌落范围约为0.7 V，恢复时间在0.15 s左右；低压直流母线电压最大电压差为0.12 V，在0.1 s左右才恢复至稳定值。而前馈控制下高压直流电压波动在0.2 V以内；低压直流母线电压波动仅在0.01 V左右，调节时间约为0.01 s。

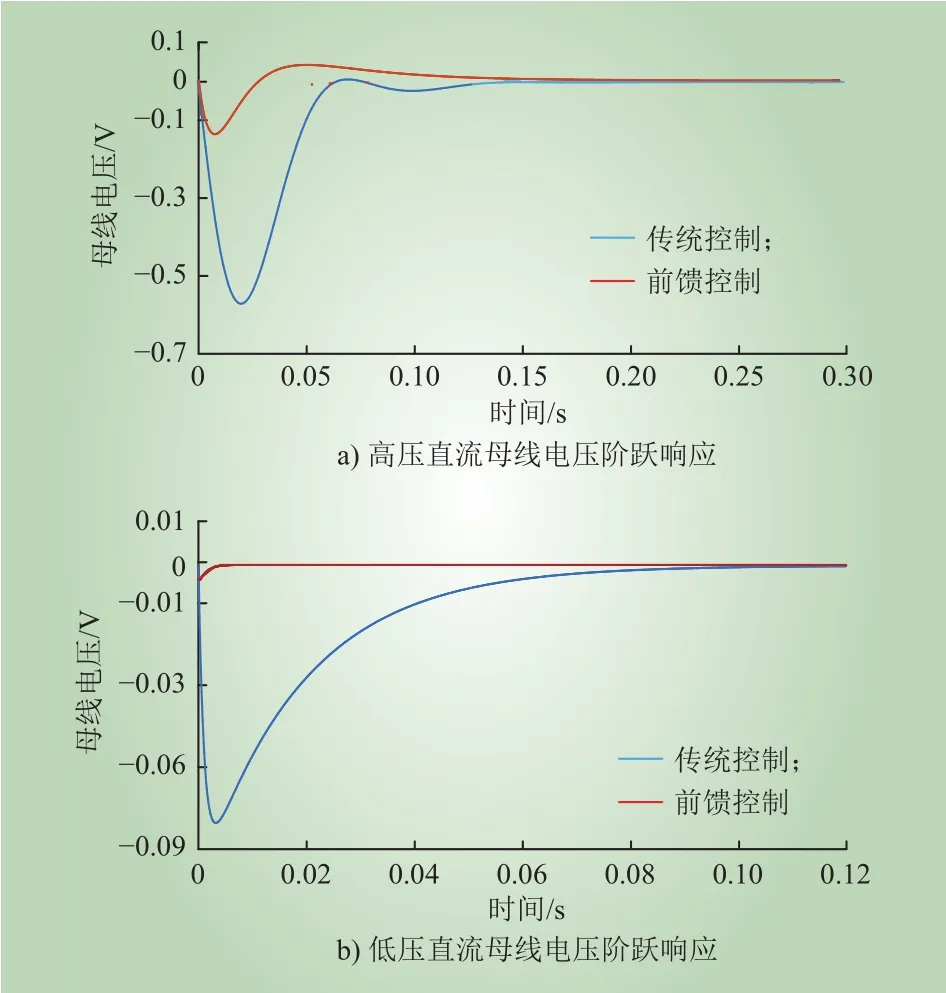
图7 不同控制下阶跃扰动响应特性Fig. 7 Response characteristics of step disturbance under different control conditions

3.2 高压侧稳定性分析

由式（14）可以直接推导出前馈控制下高压直流母线电压闭环传递函数为

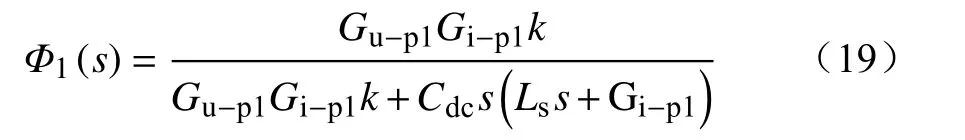
根据经典控制理论，为使闭环系统获得较好的动态响应性能和稳态性，控制器参数的取值尤其重要[24]。由式（19）可以看出，当系统参数确定后，此时系统性能由控制器4个待调节的参数kp-a1、ku-a1、kp-a2和ki-a2决定。本文通过控制变量法确定参数变化对系统性能的影响，进而选择合适的参数数值。

图8为kp-a1、ku-a1分别变化时高压侧根轨迹图。由图8可知，s1、s2为一组靠近虚轴的共轭复根，在系数kp-a1、ku-a1逐渐增加的过程中，共轭极点变化对系统动态性能的影响起主要作用。在其他参数一定，系数较小时，靠近虚轴的这组共轭复根分布在左半平面，当系数逐渐增大时，s1、s2逐渐远离虚轴，趋向负实轴。随着系数继续增大，将重新靠近虚轴，故将呈振荡衰减形式。无论电压外环系数如何变化，系统根轨迹总分布在系统左边平面，这意味着，高压侧电压平衡控制电路是稳定的。

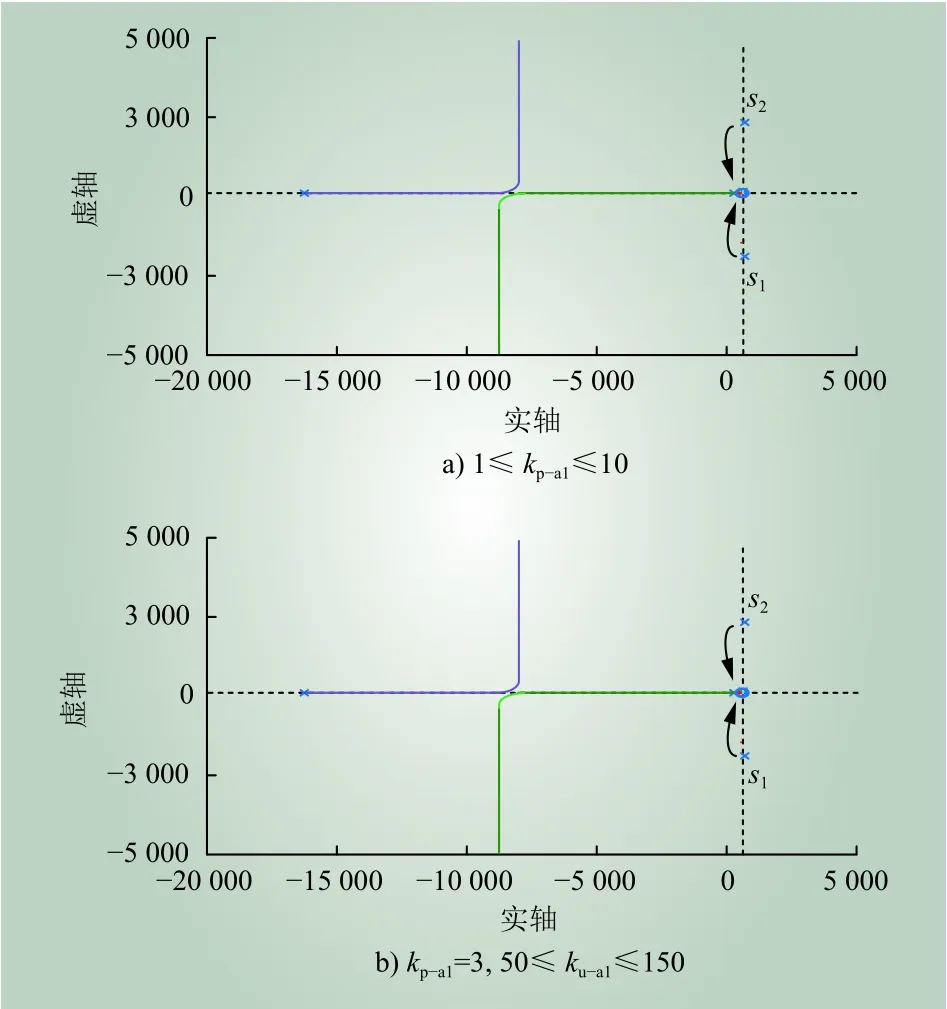
图8 电压环控制参数变化时的系统根轨迹Fig. 8 The system root locus with the change of voltage loop control parameters

图9为kp-a2、ki-a2分别变化时的根轨迹图。从图9 a)可以看出，比例系数kp-a2在3～30变化时，系统左侧极点随着系数的不断增大逐渐向右偏移，系统根轨迹总体右移，s1、s2这组共轭复根随着系数的增加，将远离负实轴，向虚轴靠近，阻尼角增加，系统超调量变大，系统稳定性变差。由图9 b)可知，积分系数ki-a2在变化过程中，左侧极点不会发生变化，s1、s2会随着系数ki-a2的增大，逐渐移动并趋向负实轴。若系数ki-a2继续增大，s1、s2沿着分离点做分离运动，此时这一特征根靠近虚轴，对系统稳定性是不利的。

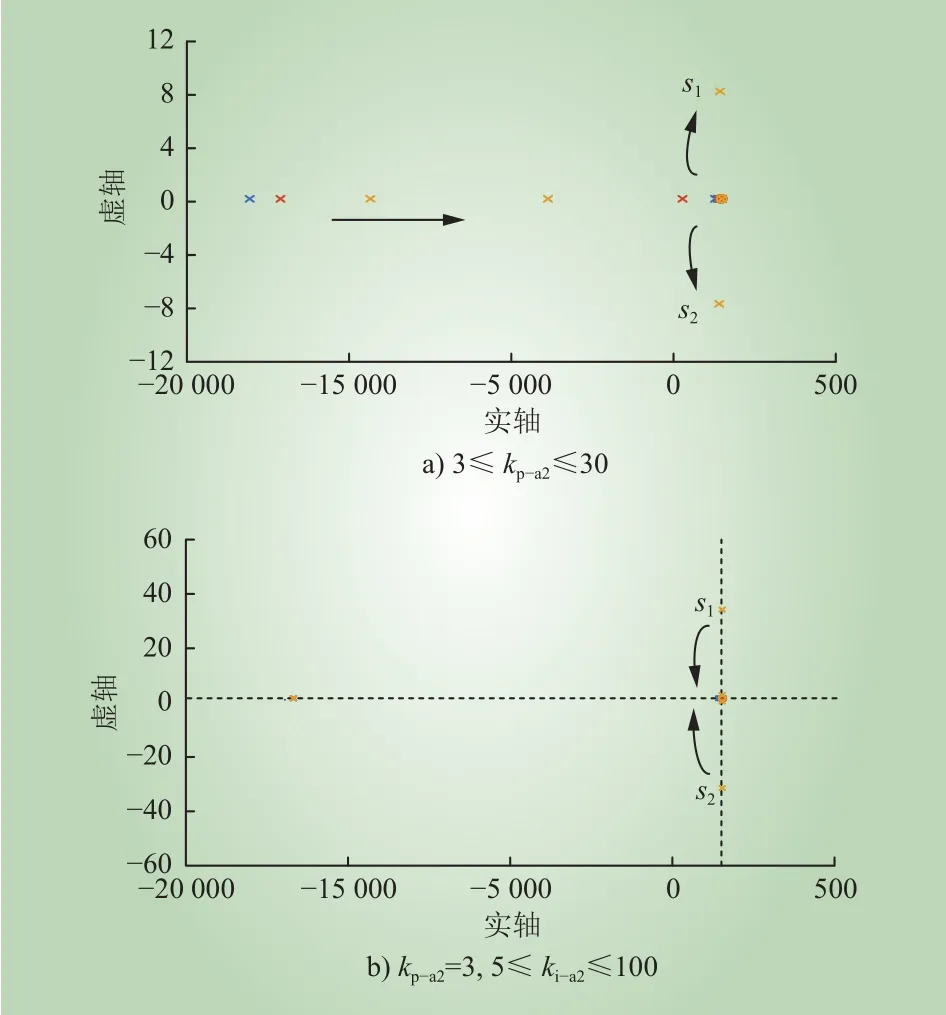
图9 电流环控制参数变化时的系统根轨迹Fig. 9 The system root locus with the change of current loop control parameters

3.3 低压侧稳定性分析

根据式（13），可以直接推导出前馈控制下低压直流母线电压闭环传递函数为

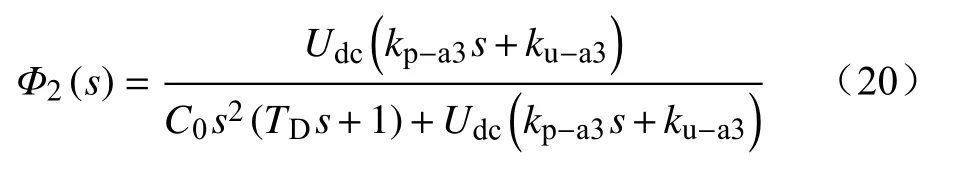
式中：kp-a3、ku-a3为DAB电压环的比例和积分系数。

根据式（20）绘制闭环传递函数的根轨迹如图10所示，表示了在比例系数kp-a3为5～30时，低压侧系统零极点变化情况。由图10可知，系统根轨迹均落在左半平面，系统总是稳定的。随着系数kp-a3的增加，系统零点和右侧极点构成偶极子且不会发生变化，左侧极点变大对系统的主导性能增强，且极点沿着分离点逐渐趋向虚轴。此时，阻尼比减小，振荡程度加剧，系统稳定性变差。

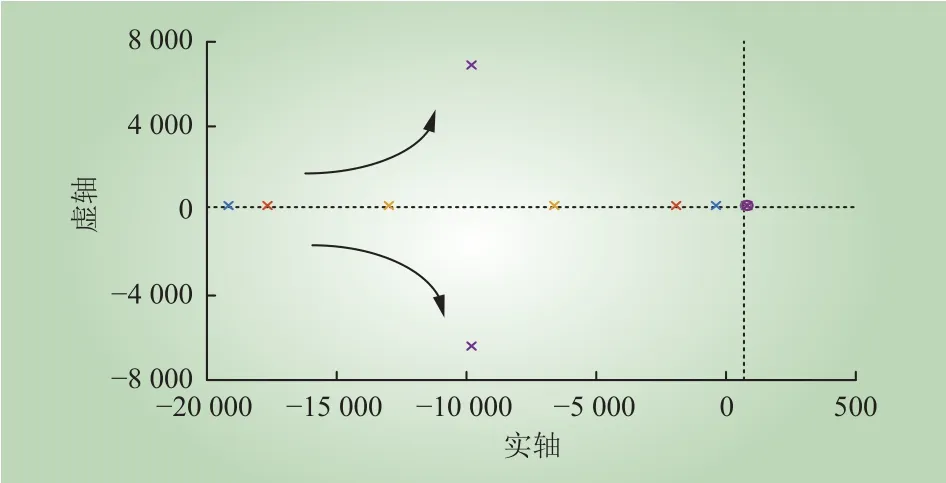
图10 DAB根轨迹Fig. 10 DAB root locus

4 仿真及实验结果

4.1 仿真验证

为了对本文所提控制策略进行验证，对图1所示结构的PET进行了测试，系统仿真参数如表1所示。

表1 PET系统参数Table 1 System parameters of PET

为验证本文提出前馈控制策略的有效性，在Matlab/Simulink搭建了系统容量为500 kV·A的3级级联电力电子变压器仿真模型。为了更好地分析控制策略的效果，设置PET负载在轻载和满载之间切换，在0.3 s时，负载由50 kW切换至500 kW；在0.6 s时，负载由500 kW切换至50 kW。

图11分别给出了负荷波动时传统控制策略和前馈策略下的仿真波形。从图11 a)、图11 b)可以看出，负荷切换时，传统控制策略下的高压直流母线最大电压波动分别为131 V和108 V，而前馈控制策略下的高压直流母线最大电压波动分别为51 V和64 V，这表明前馈控制能在负荷波动时有效抑制直流电压的畸变，波动幅值减小。

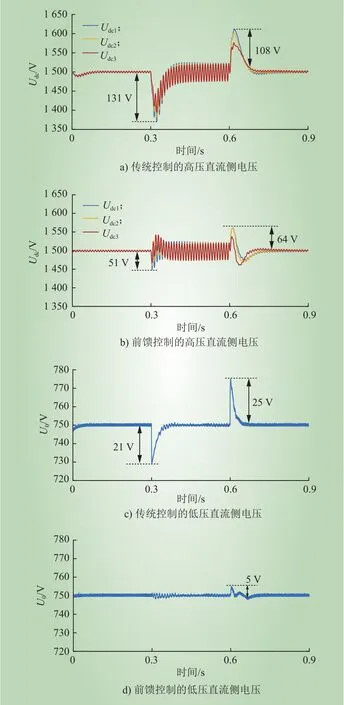
图11 PET不同控制策略下负载切换过程的仿真波形Fig. 11 Simulation waveform of load switching process under different PET control strategies

由图11 c)和图11 d)对比可知，负载切换过程中，传统控制策略下的低压直流母线最大电压差分别为21 V和25 V，而前馈控制策略下的低压直流母线最大电压差控制在5 V以内，这表明采用所提的负载电流前馈控制策略可以迅速地实现负载切换时的输出电压平衡，控制性能优越。

4.2 实验验证

为充分验证所提控制策略的有效性与优越性，根据文献[25]，搭建了半实物实验平台。主电路模型使用电磁瞬态仿真软件Starsim进行搭建，运行在基于NI-PXIe-FPGA-7846R板卡和NIPXIe-8821控制器的硬件在环系统HIL上；而控制算法模型运行在基于NI-PXIe-FPGA-7846R板卡和NI-PXIe-8840控制器的快速原型控制器RCP上。IO板卡可实现HIL与RCP之间的通信。

图12 a)给出了负荷波动时传统控制策略下电网电流和高压直流母线电压的实验波形，负荷由50 kW增加到500 kW阶跃变化的暂态过程中，高压直流母线最大电压降落为148 V，而负荷从500 kW突减至50 kW时，整流级控制的高压直流母线会存在一个电压上升，最大电压波动为132 V。图12 b)给出了传统控制策略下电网电流和低压直流母线电压的实验波形。当负荷在50 kW和500 kW之间切换时，传统控制策略下的低压直流母线最大电压波动为22 V和21 V，分别在120 ms和80 ms内恢复至稳定值。结果表明，传统策略下负载投切时，电压波形畸变较大，恢复时间长，电能质量差。

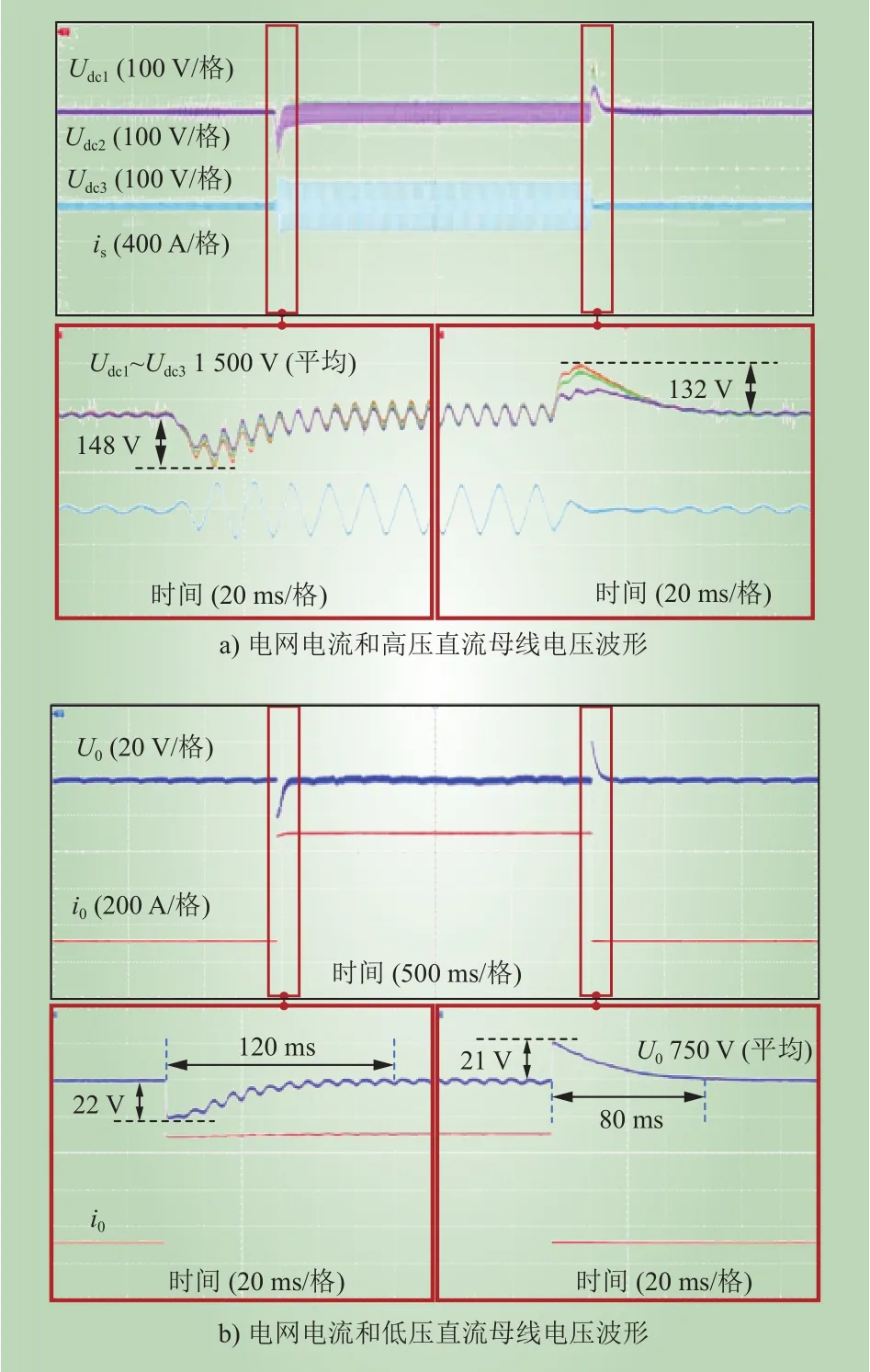
图12 传统控制策略下实验波形Fig. 12 Experimental waveform under traditional control strategy

前馈控制策略下的电网电流和直流电压的实验波形如图13 a)、图13 b)所示。由图13 a)可知，增加负荷时高压侧直流电压的冲击减小至58 V，下一阶段的最大电压波动为87 V。由图13 b)可知，前馈控制策略下低压直流母线最大电压波动为10 V和8 V，恢复时间分别为80 ms和54 ms。结果表明，相较于传统控制策略，前馈控制策略可有效降低功率切换时直流电压波动，缩短其调节时间，相比于传统控制策略动态性能显著提高。

图13 前馈控制策略下实验波形Fig. 13 Experimental waveform under feedforward control strategy

5 结论

本文针对CHB和DAB级联的PET系统直流电压波动较大的问题，在不影响原系统稳定性的同时提出了一种适用于级联系统的负载电流前馈控制方法。通过理论分析和仿真实验验证，可得出结论：（1）传统控制策略下PET动态性能较差，负荷波动会引起PET高、低压直流母线电压波动，影响系统稳定性。（2）所提控制策略引入负载电流前馈控制，能大幅度减小CHB级以及DAB级直流母线电压的跟踪误差，提升两级变换器的动态响应性能与稳定性。（3）对比传统控制策略与前馈控制策略，所提控制策略只需要一个电流传感器，降低了系统成本。