光伏变电站用氧化锌避雷器多物理场耦合分析

张天翊，梁志坚，朱瑞

(1. 广西大学 电气工程学院，广西 南宁 530004；2. 国网能源研究院有限公司，北京 102209)

0 引言

光伏系统及变电站作为新能源发电、系统能量转换与传输的重要组成部分，受到了极大关注，其安全及可靠性显得尤为重要[1-2]。然而，光伏变电站通常安装在露天区域，尤其是在雷电灾害频发的地区，雷击已经成为威胁系统设备的主要安全隐患之一[3]，因此需要对光伏变电站采取防雷措施加以保护。近年来，氧化锌避雷器以其残压低、无续流、动作时延小、通流容量大等优点，在高压及特高压输变电系统中得到广泛应用[4]。但是，随着直流输电工程的快速发展与线路电压等级的提高，避雷器出现了损耗较大、温升较高等一系列问题[5]。而温升的大小和分布对氧化锌阀片及避雷器的使用寿命有重大影响，关乎整个电力系统安全运行[6]。因此，研究避雷器温度场分布，特别是在老化等故障情况下，就显得尤为重要[7]。

目前，很多学者对电力设备多物理场进行分析，主要的方法总结为：试验法、解析法和有限元法等[8]。其中，试验方法需要加工一个实际模型，导致成本过高。此外，一些特殊工况的实验条件也过于苛刻，因此，不适用于模型的初步研究。文献[9]提出场路耦合法对500 kV避雷器进行温度场计算。光伏变电站配备的220 kV避雷器采用的是两节元件结构，在高、低压段间的电场分布发生了跃变现象。因此采用常规电磁解析方法计算损耗，再结合传热学方法对模型温度场进行分析的方法，并不是温度场分析的最优选择。此外，场路耦合方法虽然从物理概念上描述比较清晰，但是无法考虑流热耦合计算中的集肤效应、涡流效应和流体流动等影响，难以全面而准确地描述各个场的具体分布[10]。目前，有限元法采用对称正定的稀疏矩阵，可以在综合考虑对流及辐射换热效应的基础上，直接求解流固耦合方程[11]，因此能够比较全面地对电力设备的多物理场进行耦合分析。文献[12]采用有限元法计算10 kV氧化锌避雷器的温升，但是计算的是二维简化模型，忽略了热量在垂直方向的传导过程。文献[13]采用商业软件计算动车组车顶避雷器的温升，但是忽略了热辐射和空气对流换热对温度计算的影响。虽然有限元法得到了成功的应用，但是该方法是建立在区域变分原理和泛函计算的基础上，一旦网格剖分结束后就不易进行修正，因此不具备较强的自适应能力[14]。特别是在前处理过程中的网格划分十分繁琐，会占用大量时间。同时，网格扭曲或畸变现象导致计算精度差、收敛困难等问题也亟待解决[15]。因此迫切需要一种能保障计算收敛速度，满足计算精度，并且不依赖网格划分的新方法。

近年来，一种只需节点信息，无须划分网格即可构造高阶连续函数，具有较高计算精度的无网格法得到广泛应用[16-17]。但是，无网格法采用径向基函数法构造函数的近似表达式，导致计算得到的一般是节点参数而非真实节点值。因此函数不满足Kronecker特性，不能像有限元法一样便捷地施加边界条件。这也使得针对温度场计算边界的处理十分麻烦[18]。而有限元法处理边界问题比较方便，因此将有限元法与无网格法结合起来，可以较好地解决电力设备的多物理场耦合计算问题。但是，在有限元区和无网格交界面处的节点值是真实的，而无网格法的节点值是虚假的，无法直接匹配。因此，文献[19]引入由有限元与无网格法形函数组成的界面单元，虽然保证了方程求解的连续性，但忽略了交界面函数导数的连续性，而对函数及其空间导数的近似计算恰恰是无网格法求解偏微分方程的关键所在。目前，考虑鲁棒性的针对电力设备有限元与无网格法耦合计算的文献还未见公开报道。

本论文研究如何将无网格方法应用到电力设备的流-热耦合计算中，重点研究有限元求解的流体场与无网格求解的温度场在交接界面的数据传递。首先建立1台经过简化处理的某光伏变电站220 kV氧化锌避雷器三维流体场模型。采用商业有限元软件Ansys分别对其额定工作状态和老化故障下的流速分布进行计算，得到各壁面的对流换热系数。其次，通过在有限元法与无网格法交界面之间构造过渡区域，采用径向基函数法构造无网格法的形函数，推导出基于无网格法的传热学控制方程。在此基础上，建立了2种工况下的无网格温度场模型，得到了相应的温度分布。然后，将无网格-有限元法间接耦合计算结果与纯粹有限元流体-温度直接耦合仿真结果进行对比。最后通过实验，在证明了本文耦合计算方法准确性的同时，还能发现无网格计算的速度远高于有限元法。本文所述方法也可以为其他电力设备多物理场耦合分析提供一定的参考。

1 避雷器结构参数与耦合计算流程

1.1 模型主要参数

图1 避雷器三维仿真模型Fig. 1 Three dimensional simulation model of surge arrester

表1 避雷器主要参数Table 1 Major parameters of surge arrester

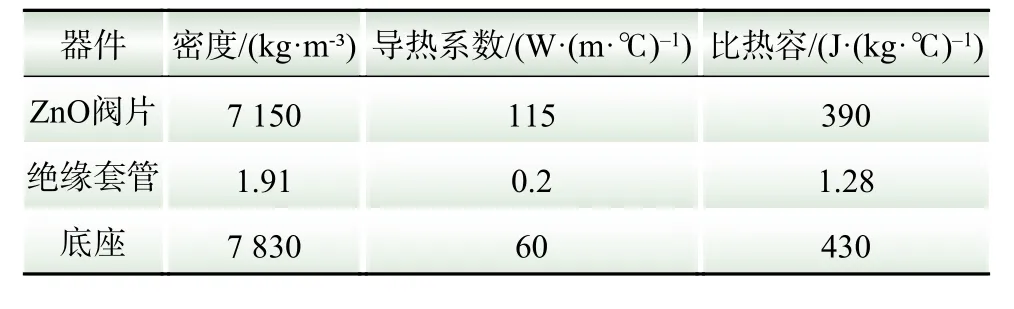
表2 材料主要参数Table 2 Major parameters of materials

为了便于分析，对避雷器做以下假设。

（1）在绝缘套管与空气之间为大空间辐射换热，因此将气体和固体交界面设置为无滑移边界[20]；

（2）流体被视为不可压缩气体，忽略浮力影响，同时忽略温度对空气粘度的影响，计算得到的避雷器壁面的对流换热系数均为平均值；

（3）假设初始温度为室温，忽略接触热阻，所有介质均可视为各向同性介质。

1.2 流体-温升耦合计算流程

无网格法与有限元法结合的氧化锌避雷器多物理场耦合分析流程如图2所示。首先，建立避雷器三维流体场有限元模型，并有如下简化处理：忽略避雷器中的一些细微结构，如不影响温升计算的退刀槽、螺纹孔、螺栓等；另外将曲率较小弧形的导角均按照直角处理；其次，对模型进行网格划分，并进行求解；然后，将流体场求解出的对流换热系数作为边界，采用有限元法对避雷器进行共轭传热计算；最后，通过在有限元与无网格计算区域中间建立过渡函数，实现流体场与温度场的数据传递。在同样的激励与边界条件的基础上，利用无网格法再次进行温度场计算，得出不同工况下避雷器温升的分布。

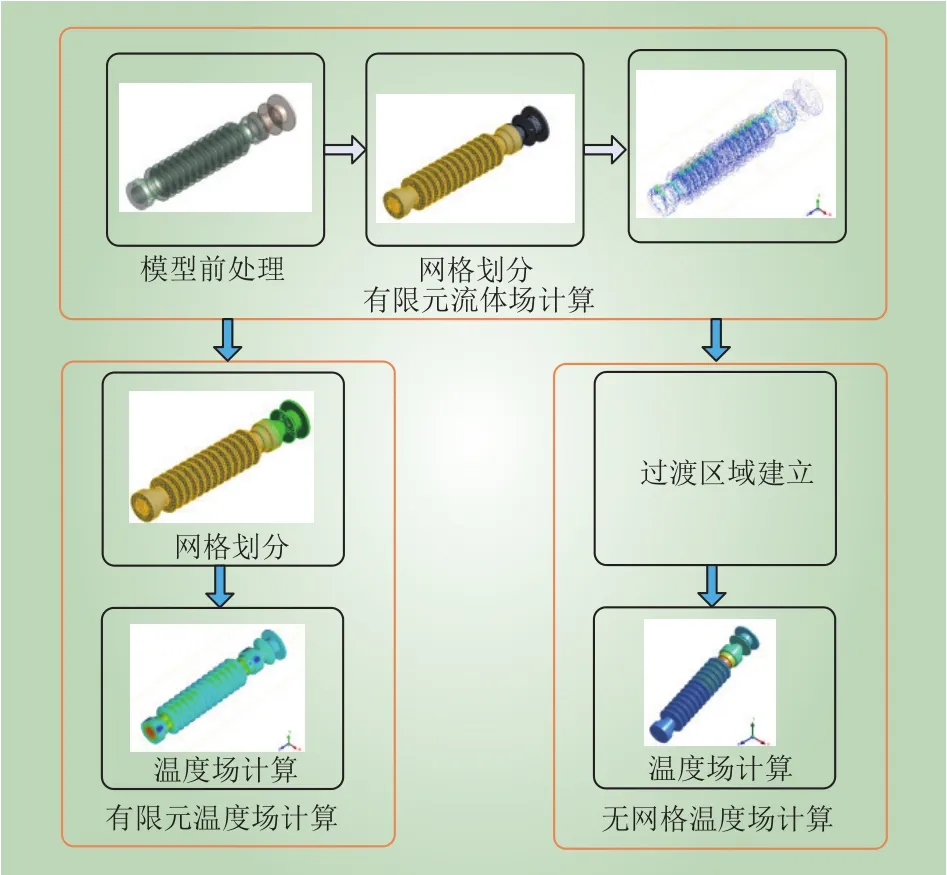
图2 避雷器多物理场耦合计算流程Fig. 2 Process of fluid-thermal coupling analysis

2 避雷器多物理场耦合数学模型

2.1 有限元法流体场控制方程

在避雷器流体场有限元计算中，主要的散热方式为自然冷却，因此气体流通模式主要为层流，满足的流体场控制方程[21]如下。

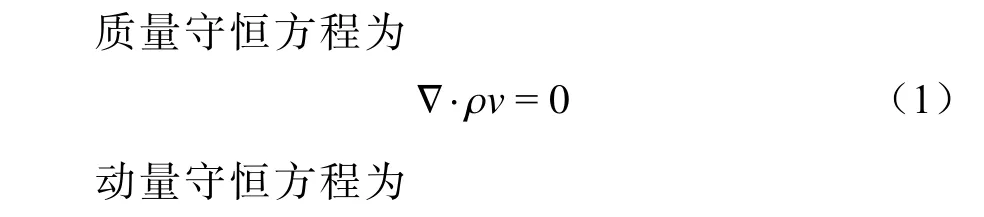
2.2 有限元法温度场控制方程

在温度场计算中，同时考虑了热传导、对流传热和热辐射的影响，其控制方程与边界条件[23]为

借助准滑移面方法研究RT位移模式非极限状态被动土压力，结果表明：绕墙顶转动挡土墙非极限状态被动土压力为凹曲线分布，越靠近墙底，被动土压力增大越快；转动越大，被动土压力越大，其合力作用点越低，合力作用点在墙高的下三分点以下。

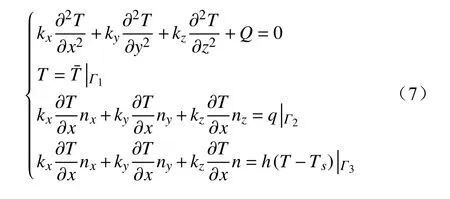
氧化锌避雷器运行时会通过套管向周围不断辐射热量，计算公式[24]表示为

式中：εt为表面辐射率，对于绝缘套管表面取为0.95，而对于氧化锌阀片则为0.71；σ为斯忒藩-玻耳兹曼(Stefan-Boltzmann)常数，文中取为5.7×10-8W/(m2▪K4)；Sto为壁面辐射面积。

最终温度场有限元离散形式为

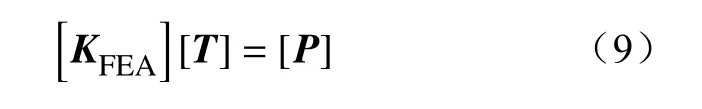
式中：KFEA为刚度矩阵；N为由四面体单元组成的形函数。

2.3 无网格法温度场控制方程

2.4 有限元法与无网格法耦合

3 多物理场耦合计算结果

3.1 流体-温度场有限元计算

图3为避雷器的网格剖分，可看出网格质量良好，符合计算精度要求。总的节点数为1 815 403，网格数为8 841 828。因此，网格划分需要占用大量的计算时间和资源，这也是本文所述无网格法优势所在。

图3 流体计算网格Fig. 3 Meshes of fluid calculation

额定运行与上节阀片老化故障时避雷器流体场粒子分布如图4所示。可以看出，在2种工况下，流体的分布区别不大，最大值分别为0.18 m/s和0.181 m/s，都出现在套管外部正上方。

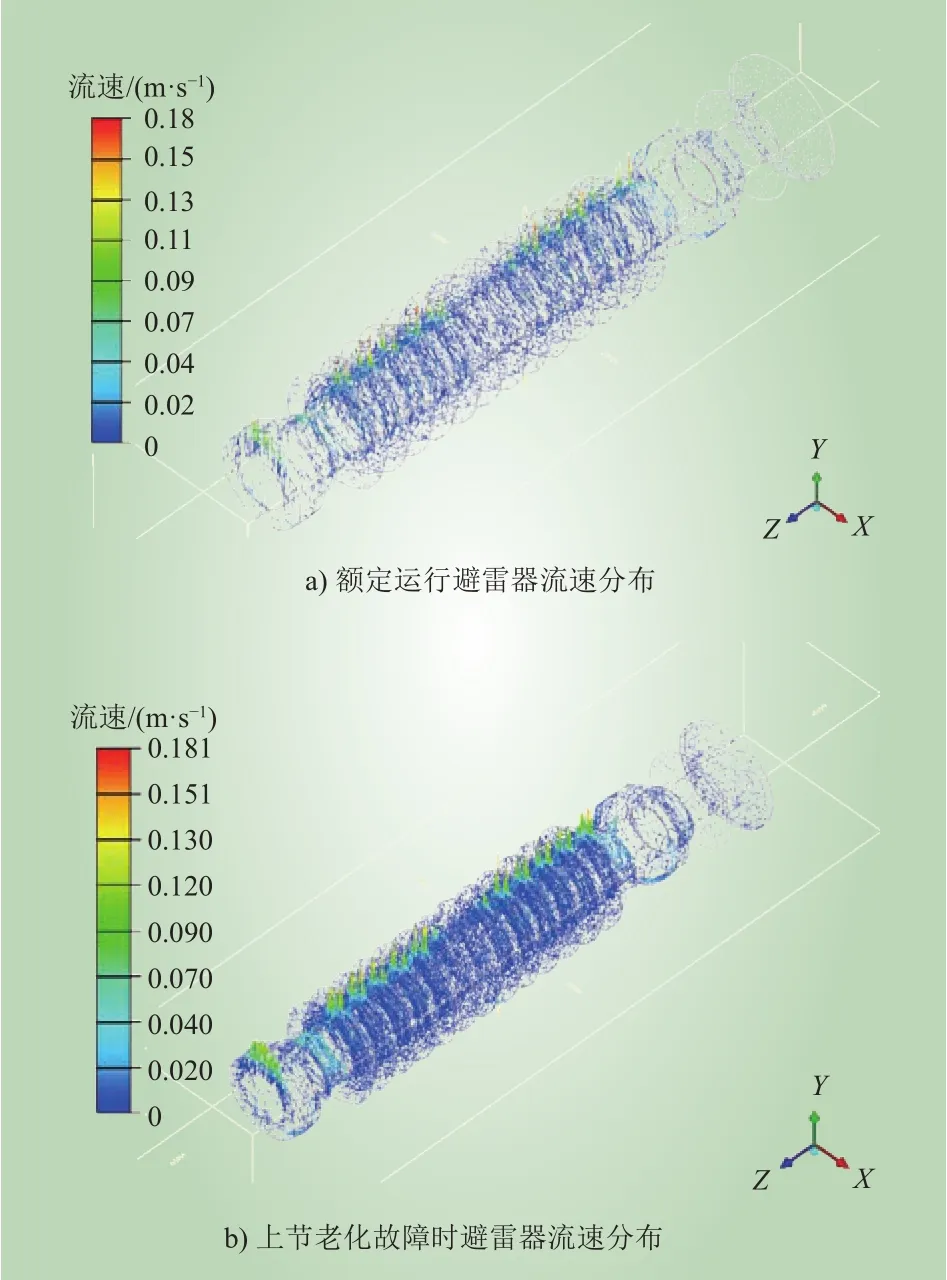
图4 避雷器流速分布Fig. 4 Flow velocity distribution of surge arrester

求出的对流换热系数可以用以下方程表示。

对于避雷器侧壁面，可表示为

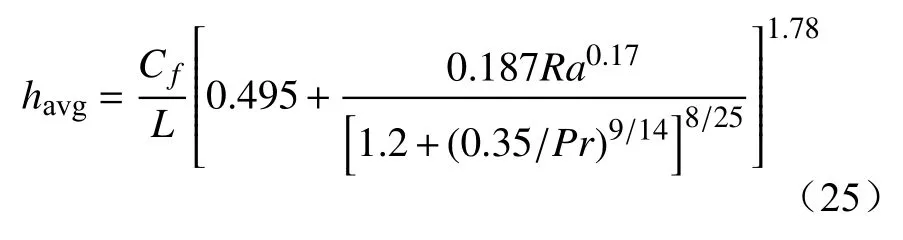
对于避雷器顶面和底面，则分别为

式中：Cf为阻力系数；Ra为瑞利数。

图5为避雷器额定运行与上节阀片老化故障时的绝缘套管表面温度分布情况。从图5 a)可以看出，正常情况下套管表面最大温升为21.65 °C，主要位于中间法兰与上节底部外套连接处。由于受到重力加速度对气体流动的影响，温度整体呈现出在竖直方向的梯度变化。图5 b)为上节老化故障情况下的温度分布，与正常工况对比可以发现，下节套管表面温升要低一些，温升最大为22.25 °C。

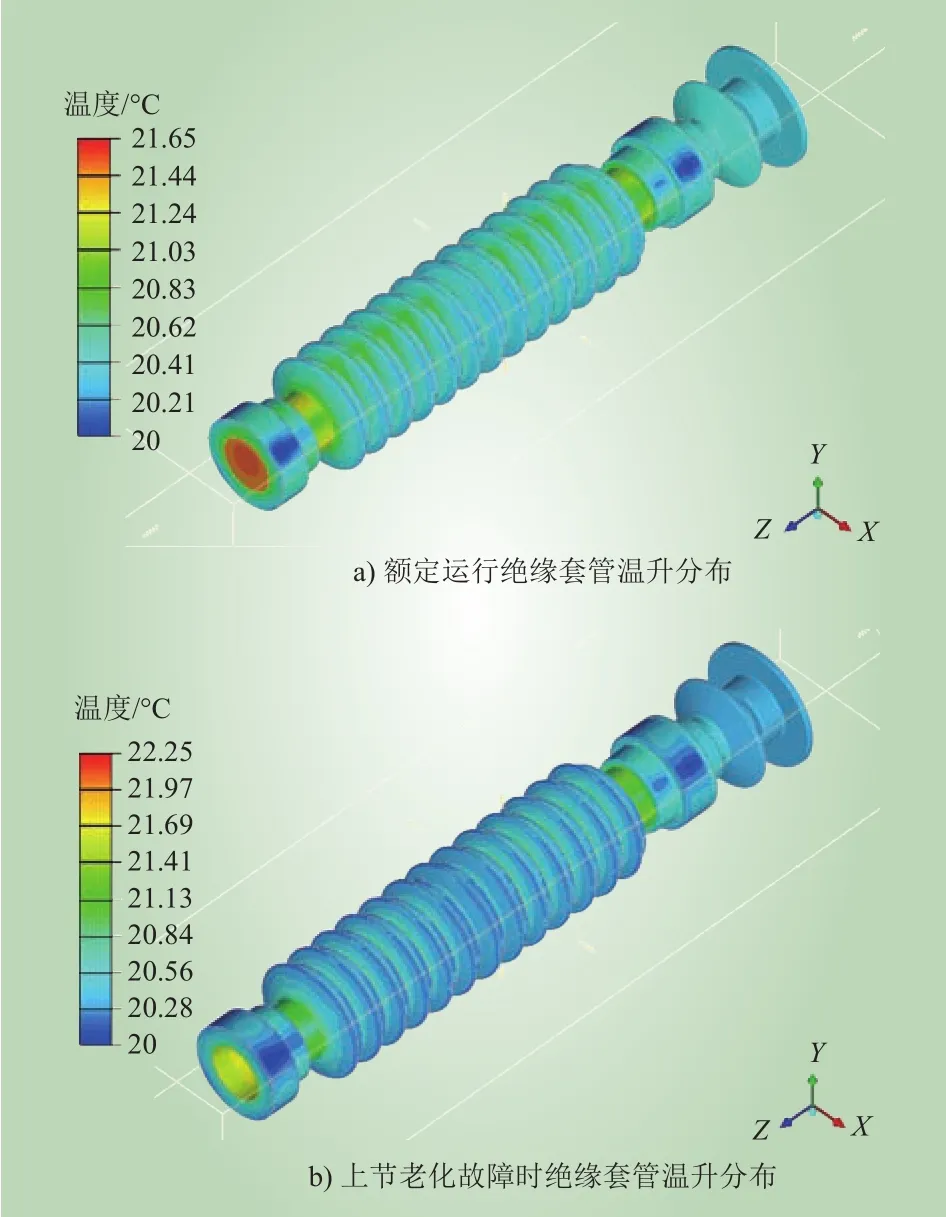
图5 基于有限元法的避雷器绝缘套管温升分布Fig. 5 Thermal distribution of arrester insulating sleeve based on FEA

图6为氧化锌阀片额定运行及老化2种状态下的温度分布情况。可以看出，在正常工况下，阀片各节均呈现出中间温度高而两端温度低的分布趋势，最高温度为31.42 °C。主要是因为避雷器内部阀片柱两端的金属连接件散热效果较好，所以温度值较低。当阀片老化故障时，最大温升为38.45 °C。可以发现老化的阀片温升要明显降低，故需要特别关注下节阀片的温升变化。

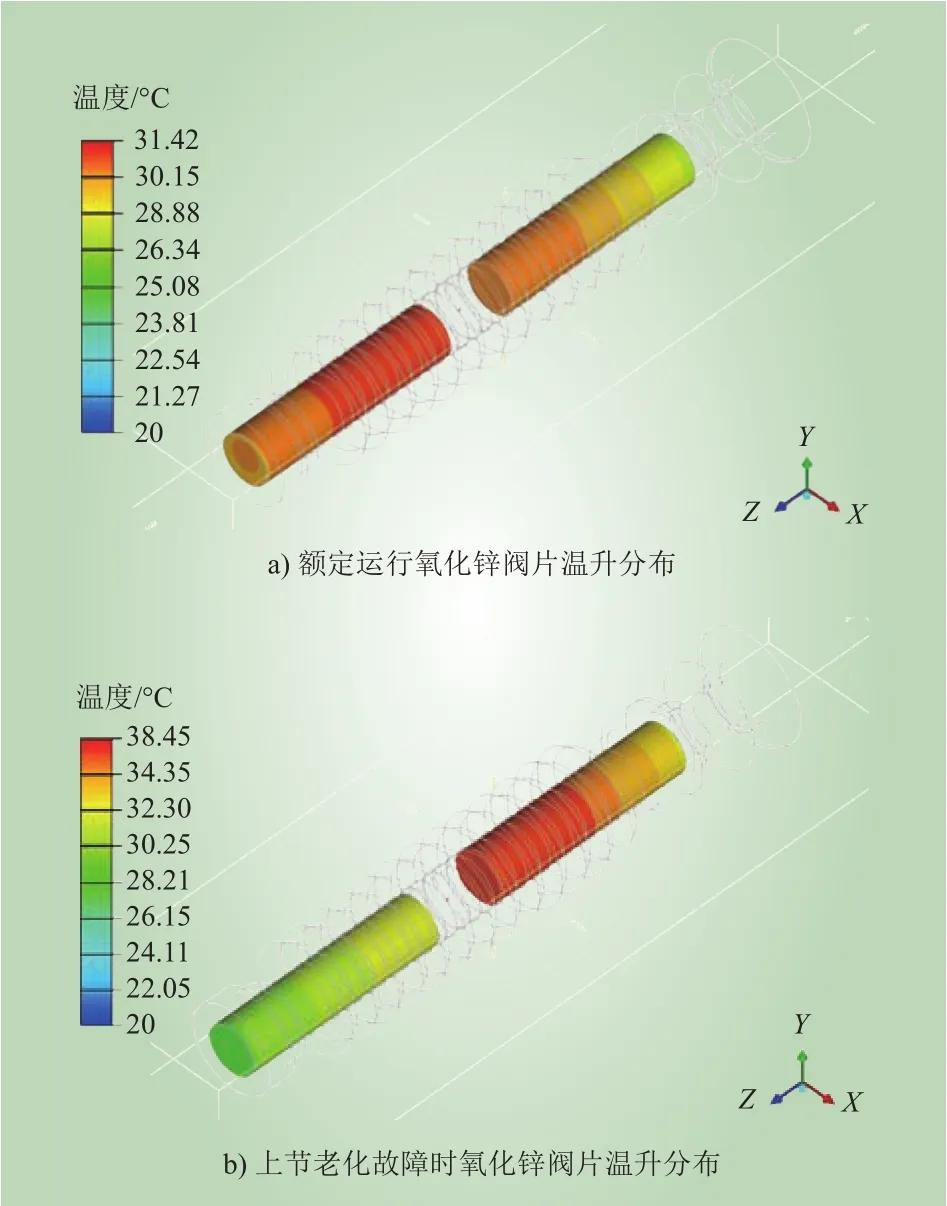
图6 基于有限元法的氧化锌阀片温升分布Fig. 6 Thermal distribution of ZnO valve plate based on FEA

出现这种现象的主要原因是当氧化锌阀片在老化时，电阻片吸收了大量的能量。在较大的热载荷作用下，内部晶界层中的离子活动非常活跃，增大了离子迁移率，导致阀片内部肖特基势垒壁高度降低，因此对过电压产生了抑制效果，有效降低了损耗[27]。此外，在长时间的大电流作用下，阀片会受到较大电磁力和热应力的影响，导致压敏电阻片内部结构发生变化，产生明显的极性效应。因此，损耗分布发生较大变化引起温升分布不均匀。

3.2 无网格温度场计算

图7为避雷器额定运行与上节阀片老化故障时绝缘套管表面温度分布情况。对比图5，可以看出二者温升分布基本相同，最大温升分别为22.22 °C 和 23.25 °C，相应的误差分别为 2.6% 和4.5%。

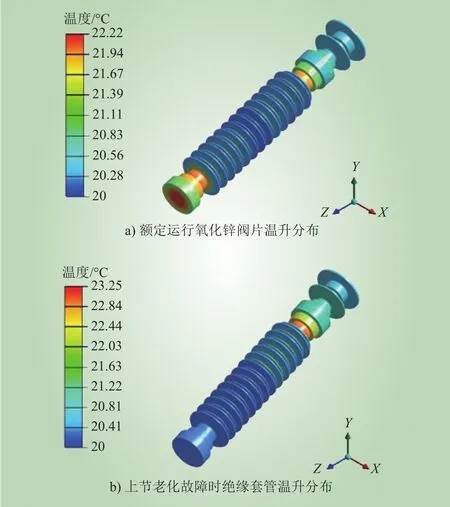
图7 基于无网格法的绝缘套管温升分布Fig. 7 Thermal distribution of insulating sleeve based on meshless method

图8为氧化锌阀片正常及老化2种状态下的温度分布情况。对比图6，可以看出计算出的温升分布基本相同。其中，无网格法计算出的阀片正常状态工况的最大温升为31.83 °C，误差为1.3%。而老化后的最大温升为38.69 °C，误差为0.6%，可以证明所用无网格计算方法有足够的精度。

图8 基于无网格法的氧化锌阀片温升分布Fig. 8 Thermal distribution of ZnO valve plate based on meshless method

表3为流体-温度耦合计算过程中各个环节的用时统计，可以发现，有限元法由于产生大量网格，计算时间远超无网格法。对比可以发现采用有限元法计算温度场消耗的时间大约是采用无网格法的210倍。

表3 计算时间统计Table 3 3 Calculation time

4 温升实验

为了验证避雷器多物理场耦合计算的准确性，按照符合国家标准GB18802.1—2011《低压电涌保护器(SPD)第1部分：低压配电系统的电涌保护器性能要求和试验方法》的规定来确定装备的温升。温度由mv2000型温度传感器来监测，检测点的安装位置如图1所示。避雷器持续工作20 h，采样时间为10 min，测量的结果如图9所示。由图9可知，各仿真结果与试验结果基本吻合，满足精度要求。structure surge arrester[J]. High Voltage Engineering, 2012, 38(8):2129-2136.

图9 温升实验结果Fig. 9 Experimental results of temperature rise

5 结论

本文提出了一种针对光伏变电站用氧化锌避雷器温升计算的新方法，构造了斜坡函数，将有限元与无网格法结合，综合了2种方法的优点。得出如下主要结论。

（1）描述了无网格-有限元耦合法的基本原理，根据温度场的控制方程，推导出了综合无网格法与有限元的温度场矩阵方程；

（2）用有限元法分别计算避雷器额定和老化工况下的流速和温升分布情况，结果显示，额定运行时，避雷器温度场分布较为均匀，而在老化故障下，氧化锌阀片温升要明显降低；

（3）采用无网格-有限元耦合法分析温度场问题时，不仅能够保障计算精度，还能够极大地提高计算效率。此种方法对配置在光伏变电站内的电气设备数值计算具有一定的参考价值及意义。