基于改进鸽群算法的台区三相负荷不平衡相序调整方法
胡明月,张慧芬,苗淑平,杨帆,曲振明
(1. 济南大学 自动化与电气工程学院,山东 济南 250022;2. 国网山东省电力公司济宁供电公司,山东 济宁 272100)
0 引言
低压配电台区作为电力系统的末端与用户直接相连,该区域的电能质量和人们的生产生活密切相关。目前中国配电网中三相不平衡现象非常普遍,在低压台区,除了少数负载是三相用电,大部分用户负载是随机性接入的单相用电,负荷分布不均是导致台区三相不平衡现象长期存在的主要原因。三相不平衡会对电力系统的供电安全、电能质量和经济运行产生不良影响,是配电网运行的主要薄弱环节之一[1]。不平衡生成的零序电流会引起电力线路、配电变压器内部发热,产生额外的能量损耗。用电设备的安全运行受到干扰,负载重的某相上部分设备低于额定电压运行,而负载轻的相上设备可能因过电压烧坏。目前常用的低压配电台区负荷平衡装置主要有换相开关型[2-4]、电容型[5-6]和电力电子型[7-9]3种。其中,换相开关型三相负荷自动调节装置在不改变配网原有框架结构的情况下,通过调节不平衡负荷的相序,使负荷平均分配到三相[10]。本文研究一种基于该装置的负荷相序调整方法,降低台区三相电流不平衡度。
优化算法是负荷相序调整的关键,算法的选择直接关系到控制装置能否求得最优的换相结果。运用传统算法求解时,需要用穷举法列写出所有接在电流最大相的负荷换相至最小相的情形[11],通过预计算更改部分负荷的相序,但实际调节效果受到负荷原始分配的制约,不能保证在所有情况下得到最优的调整方案。文献[12-13]将相序调节按照负荷转移方向分为两相转移到一相、一相转移到两相2种情况,分别给出了详细的调控策略,然而不平衡度过大时,局部负荷需要连续多次动作完成调整。人工智能算法[14-16]在数据处理和计算能力方面具有显著优势[17-18],可以仅通过单次换相达到理想的不平衡调节效果。文献[19]利用遗传算法计算对用户负荷相序进行灵活调整,但是该方法的收敛速度较慢,计算效率有待提升。文献[20]采用加速粒子群算法,求解不平衡度最小和切换次数最少的换相方案,但是迭代后期种群间距较小,容易过早收敛,陷入局部最优。
上述传统优化算法的有效性易受负荷分布影响,本文采用人工智能算法,突破初始解的限制,解决复杂的多维数学问题。针对现有人工智能算法寻优效率较低,容易陷入局部最优解的问题,本文引入自适应参数和柯西扰动对鸽群算法进行改进,利用改进的鸽群算法求解负荷换相方案。
1 相序调整策略和优化换相数学模型
换相后配电台区三相不平衡程度能否降低,是判断负荷相序调整策略有效性的重要标准。设IA、IB、IC分别为A、B、C三相电流,本文根据配电网运维规程[21]计算三相电流不平衡度 ΔIABC为
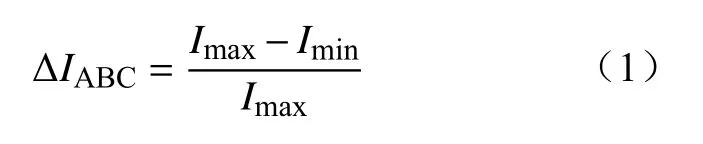
式中:Imax为三相中最大的电流值;Imin为三相中最小的电流值。
本文运用换相开关型负荷自动调节装置对不平衡负荷组实行在线实时调整,负荷调控方法参见文献[19]。从台区主变压器(下简称主变)低压侧装设一台控制器,并选择30%左右的用户负荷,在用户组进线处安装若干个换相开关。控制器采集配电变压器出口处的电压电流,计算台区的三相电流平衡度,当电流不平衡度超过规定值并持续一段时间,控制器读取换相开关处所采集的负荷侧电压电流和相序信息,以此为依据计算得出最佳换相方案,对部分负荷组相序进行调整。
求解最优换相方案时,主要考虑相序改变对不平衡度的影响,认为当台区三相负荷完全平衡时,三相电流也达到完全平衡。本文以台区主变低压侧三相电流不平衡度最小为目标进行换相。设共有D台换相开关,xk表示第k(k≤D)台换相开关所连接的负荷相序,D台换相开关所连接的负荷相序组合用向量X表示,则目标函数表示为
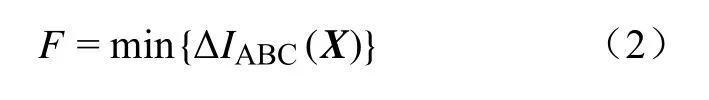
约束条件为各线路电流不超过线路最大允许载流量,即

式中:Ik为第k(k≤D)台换相开关采集到的负荷电流;Ikmax为线路最大允许载流量。
进行用户相序调整时,未安装换相装置的负荷组所连接相序保持不变,运用换相开关动作调整部分负荷组相序,改变台区主变低压侧三相电流,使之不平衡度最小。通过负荷相序调整,将台区不平衡度控制在国家标准以内,减少线路和变压器上的电能损耗,确保用电设备安全运行。
2 优化换相数学模型的求解
2.1 改进的鸽群算法
式(2)所示的最优换相模型是一个非线性离散数学模型,可以利用鸽群优化算法求解(pigeoninspired optimization,PIO)。鸽群优化算法作为一种基于群体智能的全局优化算法,实行随机并行搜索,不受函数类型和初始解的限制,能够快速解决复杂的多维数学问题。该算法自提出后,在实际应用中取得了众多成果,适用于无人机编队、控制参数优化、图像处理以及生命科学等许多个领域[22-23],但和其他许多群体智能算法一样,该算法亦存在过早收敛而容易陷入局部最优解的问题。当运用鸽群算法求解负荷相序调整方案时,种群能够快速收敛到一个相对优质的位置。然而由于缺乏全局意识,往往不能寻找到最佳的目标,多次重复运行会得到几个不同解。
为避免过早收敛,本文对地图和指南针因子R进行自适应改进,更好地平衡全局搜索和局部搜索;同时在迭代过程中引入柯西变异,当连续多代全局最优值未发生改变时,外界施加柯西扰动,促使种群保持多样性。
鸽群优化算法的主要思想来源于鸽群飞行途中寻找目的地的过程,通过模仿鸽子在寻找目标的不同阶段使用不同导航工具这一机制,提出地图和指南针算子以及地标算子2种不同的算子模型[24]。飞行初期,鸽子依靠磁感绘制地图,每一次迭代中,通过比较自身和当前种群内适应度值最佳个体的位置,不断调整飞行的速度和方向。
地图和指南针因子更新公式为
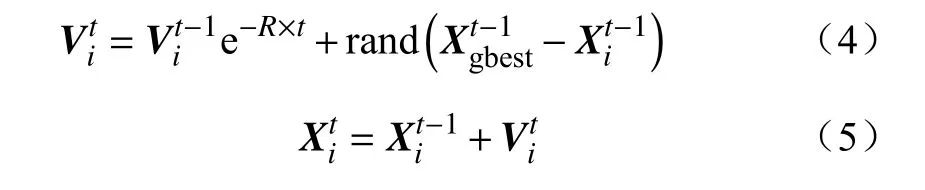
式中:t为当前迭代次数;Xi和Vi为鸽子i对应的位置和速度;R为地图和指南针因子;表示第t次迭代全局最优个体位置。
更新后鸽子的位置,既继承了上一代个体位置和速度,也受到当前全局最优个体与上一代个体相对位置的影响。地图和指南针因子R用于控制鸽子的速度,决定着鸽子受原来个体速度影响的程度,当R较小时,鸽子继承了较大的速度,能够快速收敛,拥有更好的全局搜索能力;当R很大时,鸽子速度较小,便于在局部进行细致的搜索。为提高搜索效率,自适应地改变地图和指南针因子,使鸽群的关注点在寻找目标的过程中由全局转向局部,构造地图和指南针因子R关于迭代次数t的函数。令
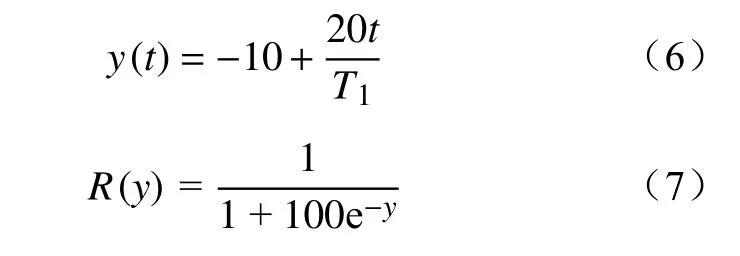
式中:T1为设置好的地磁导航次数。迭代初期t较小,地图和指南针因子R值从接近于0的极小值开始,随着中间变量y的增加缓慢增长;当t达到预设总导航次数一半时,R开始快速增加,增幅先变快后渐缓,临近迭代结束时数值趋近于1。通过自适应地改变地图和指南针因子R,能够满足期望,较好地平衡全局搜索和局部搜索。
飞行后期接近目的地时,鸽子改变导航工具,运用目的地附近熟悉的地标进行导航。在每一次迭代后淘汰鸽群内部适应度值较低的一半群体,计算剩余群体中的中心位置,以此作为地标。鸽子逐渐调整飞行方向朝地标位置靠近,继续迭代至最大地标导航次数。
地标算子更新公式为
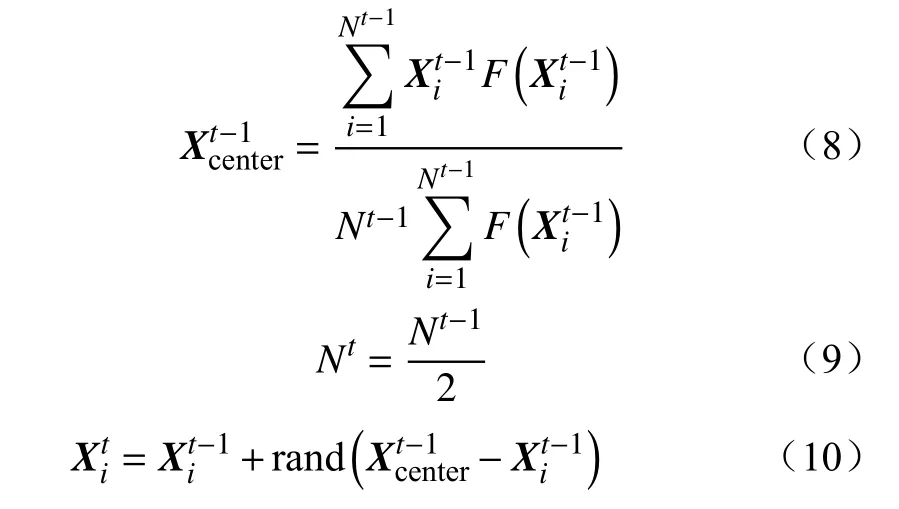
鸽群飞行过程中,当多数鸽子都聚集到同一范围内时,随着它们之间距离的拉近,飞行速度会逐渐放缓,甚至停滞不前。为避免算法过早收敛陷入局部最优,本文在迭代停滞时施加柯西扰动。设置一个阈值,当连续多代最优适应度函数值未发生改变时,认为候选解很大可能陷入了局部最优。此时,对当前全局最优位置实施柯西扰动[25]。
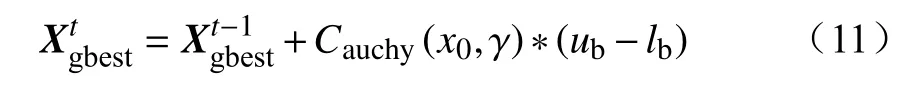
式中:Cauchy(x0,γ)是服从柯西分布的随机变量;x0和γ分别为柯西分布的位置参数和尺寸参数,此处取0和1;ub和lb为解空间的上、下界。
计算扰动后位置的最优适应度函数值并和原来的函数值比较,若扰动后更优,则把当前全局最优位置更新为扰动后的位置。柯西扰动重分布策略对全局最优位置进行干扰,能够迫使个体持续运动,连续跳出局部最优解。
经过上述改进后的鸽群算法记为NPIO(new pigeon-inspired optimization,NPIO),该算法不受函数类型限制,适用于解决复杂的多维问题。
2.2 利用改进的鸽群算法求解负荷相序调整方案
使用换相开关型三相负荷自动调节装置治理台区内部负荷不平衡,选择低压配电台区内的若干节点装设换相装置。换相开关控制负荷连接的相位,正常工作时投切于A、B、C三相之一。整个台区D台换相装置所连接的负荷相序状态组合可以用行向量X表示为
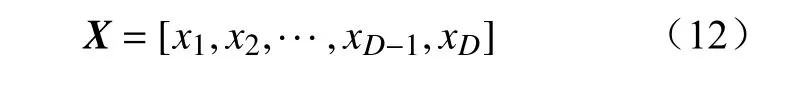
依据改进的鸽群算法,求解最优负荷相序状态组合的主要工作如下。
(1)编码。求解负荷相序调整方案时,首先要对换相开关所连接的负荷相序编码,将实际问题转化为算法能够接受的数学表达形式。本文用1到3之间的整数表示换相开关的3种工作状态:xk=1表示负荷接入A相;xk=2表示负荷接入B相;xk=3表示负荷接入C相。配电台区内部所有换相装置所连接的负荷相序状态组合,可以用D个1到3的离散数字组成的行向量X表示。
(2)初始化。初始化阶段,在搜索范围内随机生成鸽群的初始位置,以生成的初始化群体为基础进行迭代操作。算法中每只鸽子的位置都代表一组换相开关的连接状态,代表一种负荷相序的组合方式。用式(12)中的向量X表示一只鸽子的位置,算法开始迭代前,依据编码原则对鸽群的位置和速度进行随机初始化。假设整个鸽群中有N只鸽子,则初始化时生成N×D维矩阵Z,矩阵中的每一行都代表一个个体编码。

(3)计算适应度函数。适应度函数用于评估每只鸽子位置的优劣,常采用目标函数计算鸽群中每个个体的适应度值。本文的目标函数是台区变压器低压侧三相电流不平衡度最小,可以通过式(1)计算得到。每一组负荷相序状态都对应一个适应度函数值,适应度函数越小,对应的负荷相序组合越优,选择适应度函数值最小的鸽子位置为全局最优位置。
(4)地磁导航。确定鸽群初始位置后鸽子进入地磁导航阶段,依据式(4)(5)迭代。自适应变化的地图和指南针因子R随迭代次数的增加而增加,需要在每次地磁导航前通过式(6)(7)计算新的R值。每只鸽子通过比较自身和当前种群内适应度值最优鸽子的位置,调整飞行的速度和方向。算法运行过程中,每次完成迭代都要对全局最优位置更新。
(5)地标导航。算法运行到地磁导航的最大迭代次数后,鸽群转换导航工具,进入地标导航。地标导航的过程中,每次迭代都要淘汰种群内部适应度值较低的一半鸽子,并依据式(8)~(10)计算剩余群体中的中心位置得到新的地标。达到地标导航最大迭代次数时,改进的鸽群算法运行结束。输出的全局最优位置,就是本文求取的台区换相开关连接相序。
在地磁导航和地标导航的过程中,如果连续多代最优适应度函数值未发生改变,代数达到阈值,则对当前全局最优位置进行柯西扰动,迫使鸽群继续飞行,跳出局部最优解。运用改进的鸽群算法求解负荷相序调整方案流程如图1所示。
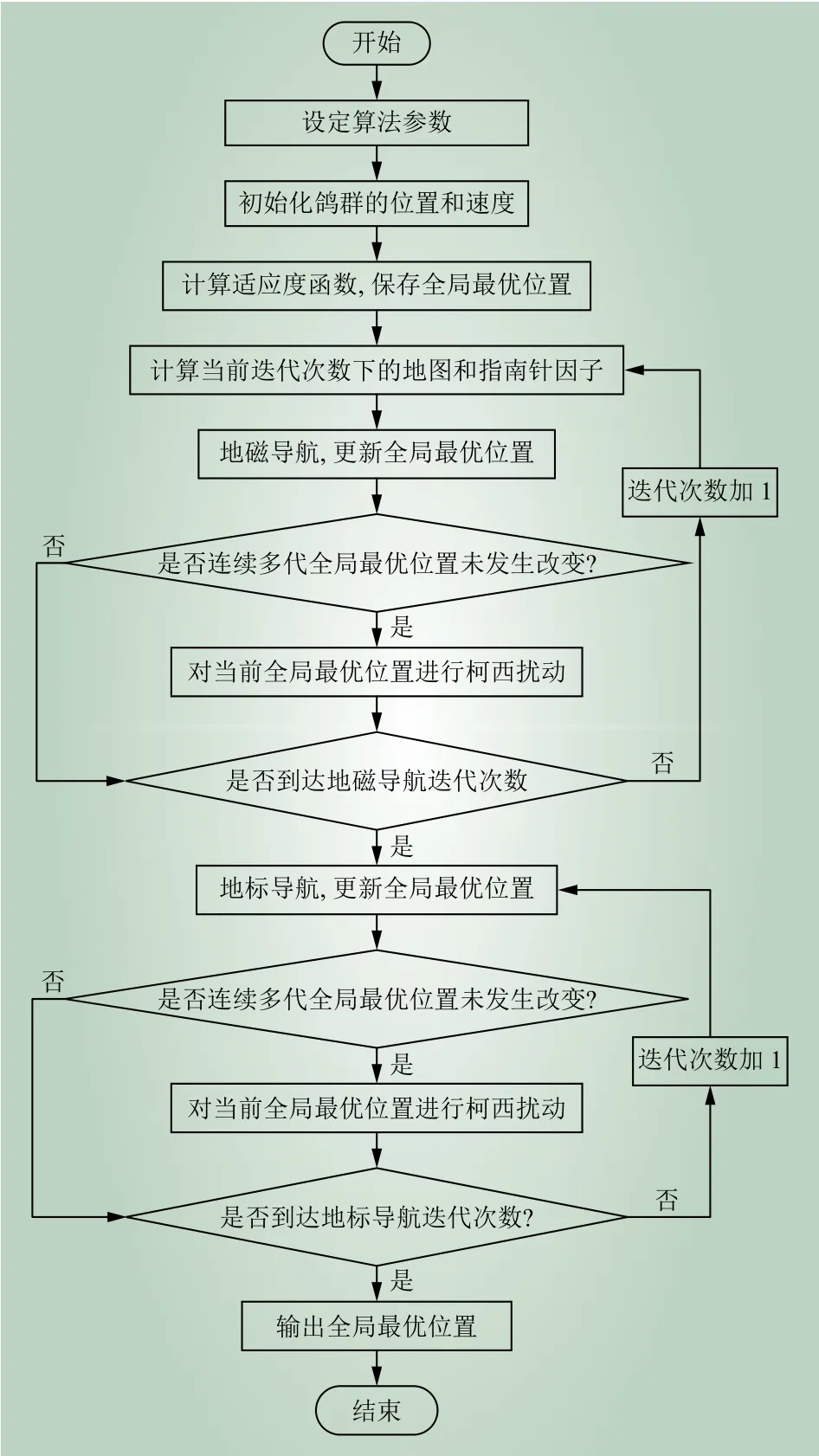
图1 改进的鸽群算法求解负荷相序调整方案流程Fig. 1 Solution process of load phase sequence adjustment scheme based on new pigeon-inspired optimization
3 算例分析
为验证上述三相负荷不平衡相序调整方法的可行性,本文以沙梨乡一配电台区为例,在Matlab仿真平台上搭建换相模型。该台区由34个节点构成,用户负荷分散,配变低压侧A相电流105 A、B相电流116 A、C相电流154 A,由式(1)计算不平衡度高达31.81%,超过配电网运维规程[21]中15%的限值。为解决此台区内三相不平衡问题,依据各节点的负荷容量,结合负荷用电性质以及不平衡治理的经济效益,选择节点安装换相装置,台区负荷分布及换相装置配置情况如图2所示。
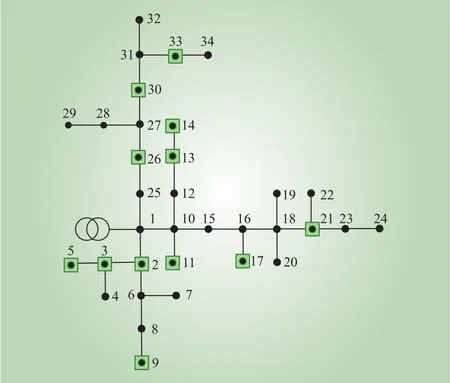
图2 台区负荷自动调节装置配置Fig. 2 Configuration of automatic load regulation device in station area
3.1 改进鸽群算法求解换相方案
利用改进的鸽群算法计算相序调整方案,算例中共含12个换相装置,设定搜索空间维数D=12,种群数量N=30,地磁导航次数T1=35,地标导航次数T2=15。随机初始化鸽群的位置和速度,计算鸽群中个体的不平衡度,将不平衡度最小的鸽子位置作为全局最优位置保存。然后,进入地磁导航阶段,计算当前迭代次数下的R,代入地图和指南针算子更新公式。地磁导航35次后,鸽群开始地标导航,通过地标算子更新公式迭代15次。每次迭代后都更新全局最优位置,连续多代全局最优值未发生改变时施加柯西扰动。导航结束后,输出全局最优位置即换相后各节点相序。比较得到共有9个换相装置动作,换相后配电低压侧A相电流125 A、B相电流124 A、C相电流126 A,负荷电流不平衡度由31.81%降至1.59%,小于配电网运维规程[21]中要求的15%。换相前后各节点换相开关连接相序如表1所示。
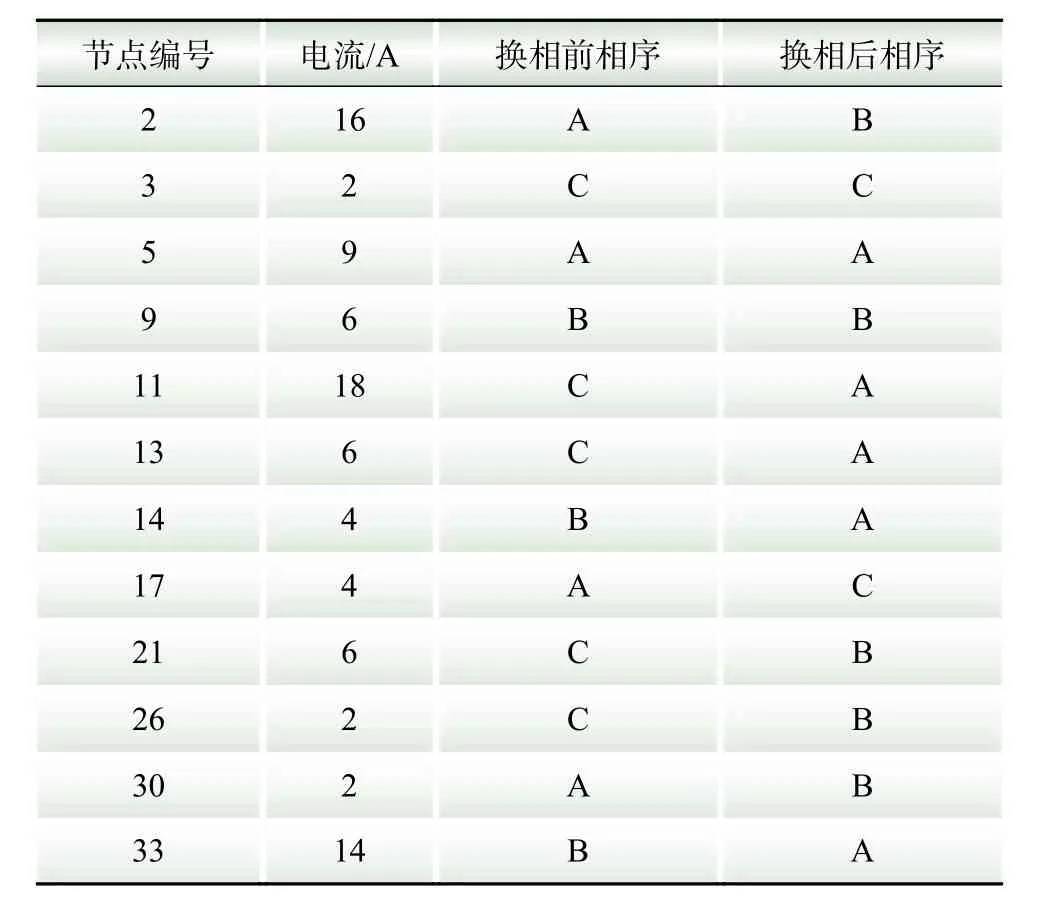
表1 各个节点电流及换相开关相序Table 1 Node current and commutation switch phase sequence
0.075 s时换相开关发生动作,图3为换相前后变压器低压侧三相电流、电压、中性线电流及重载相负荷电压情况。由图3 a)可见,换相前配变低压侧电流不平衡严重,最大相与最小相电流相差近50 A,换相后不平衡度显著降低,各相电流基本平衡;由图3 b)可见,换相前电压中性点电位偏移,B相电压较低,A、C相电压较高,换相后三相电压相对均衡,不平衡状况得到改善;由图3 c)可知,换相前中性线电流超过30 A,引起额外的电能损耗,换相后中性线电流下降了66.7%,维持在10 A以内;由图3 d)可知,换相前重载相负荷电压仅为198 V,换相后上升到208 V,提高了5.05%。仿真结果表明,基于NPIO算法的换相方案能够有效治理三相负荷不平衡。
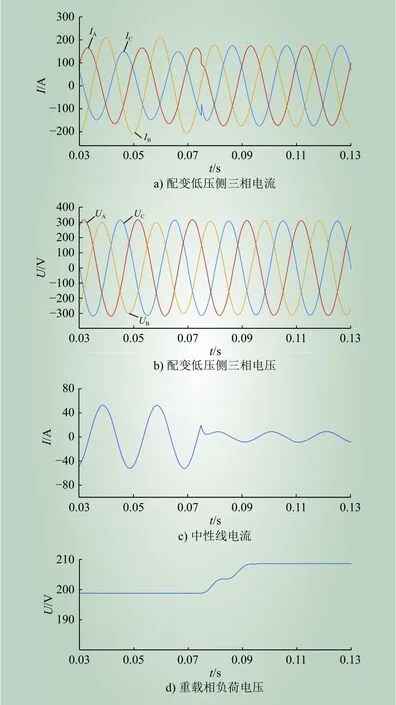
图3 换相前后配变低压侧电流、电压、中性线电流、重载相负荷电压情况Fig. 3 Low-voltage side current, voltage, neutral line current, and heavy-load phase load voltage of distribution transformer before and after commutation switch
3.2 改进鸽群算法与其他算法对比
分别用遗传算法(genetic algorithm,GA)、蝙蝠算法(bat algorithm,BA)、粒子群算法(particle swarm optimization,PSO)、人工蜂群算法(artificial bee colony,ABC)和基本鸽群算法(pigeon-inspired optimization,PIO)求解上述算例的相序调整方案,与改进鸽群算法的计算结果比较,各算法优化过程中的三相不平衡度迭代曲线如图4所示。可以看出,NPIO与其他算法相比表现更好,能够在迭代过程中连续跳出局部最优解,最快求得三相不平衡度最小的负荷相序调整方案。
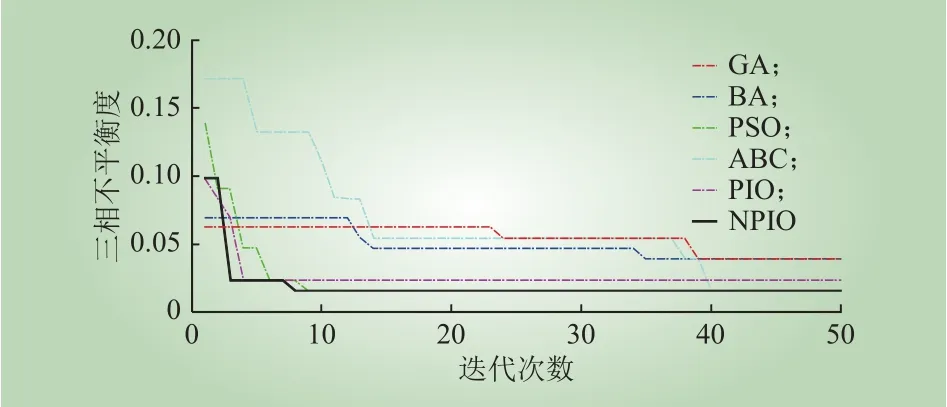
图4 各个算法三相不平衡度迭代曲线Fig. 4 The three-phase unbalance iterative curves of different algorithms
为进一步验证NPIO算法的性能,各个算法分别独立运行50次,计算其负荷不平衡度平均值、负荷不平衡度标准差和平均收敛速度,统计如表2所示。
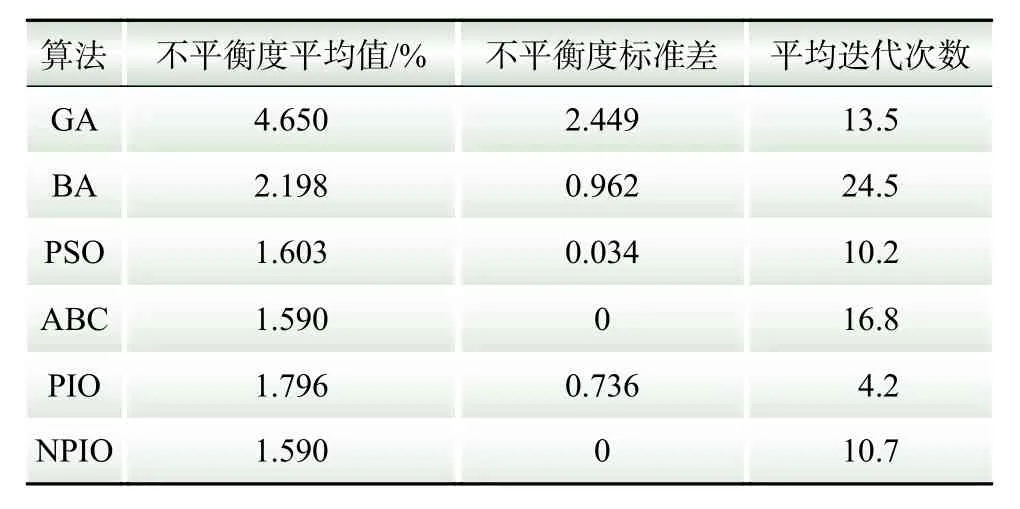
表2 各个算法的性能比较Table 2 Performance comparison of different algorithms
由表2可见,GA的负荷不平衡度平均值和标准差最大,最容易收敛到不平衡度1.59%以外的局部最优解。BA的收敛速度落后于其他算法,种群需要迭代约24.5次才能得到运算结果。PIO的平均迭代次数最小,运算速度最快,但难以保持较高的种群多样性,计算结果存在偏差。ABC鲁棒性好,负荷不平衡度标准差为0,能够稳定求取最优换相方案,然而寻优效率较低。PSO和NPIO都具有优良的性能,但前者的治理效果不够稳定,有时优化换相后的负荷不平衡度并非最小值。比较可知,求解负荷相序调整方案时,NPIO在快速性、准确性和稳定性3方面综合表现更为突出,每一次运算都能得到三相不平衡度最小的换相方案。同时,算法满足收敛速度的需要,运行10代左右得到结果。
4 结论
针对低压配电台区长期存在的三相负荷不平衡现象,本文研究了一种基于换相开关的负荷相序调整方法。运用不平衡负荷换相控制策略调换部分用户的相序,平均分配三相负荷。
(1)以配电变压器低压侧三相电流不平衡度最小为目标,考虑线路最大允许载流量的约束,建立了台区优化换相数学模型并制定了负荷相序调整策略。
(2)引入自适应参数和柯西扰动对原始鸽群算法进行改进,提高算法的种群多样性,帮助个体连续跳出局部最优解。改进后鸽群算法能够兼顾通用性和收敛性的要求。
(3)利用改进的鸽群算法求解负荷相序调整方案,Matlab仿真证明了此方法能有效降低台区三相电压电流不平衡度,减小中性线电流,提高重载相负荷电压。该算法克服了过早收敛的缺点,与GA、BA、PSO、ABC、PIO相比,在快速性、准确性和稳定性3方面综合表现更为突出。

