基于综合能源计量数据的区域用能特性分析

王新刚，赵舫，朱文君

(国网上海市电力公司电力科学研究院，上海 200437)

0 引言

智能化电力网络集发输配用于一体，与国民经济运行息息相关。随着用户对供电质量的要求越来越高，智能电网在用户侧的革新已迫在眉睫。

当前智能电网正在引进更多的新成分和新技术，并逐渐发展为一个越来越复杂的综合性系统，对电网调度管理机制提出了全新要求。在电网企业制定重要决策时，深入了解用户的用电行为习惯至关重要[1-3]。对一定区域内的用电行为进行分析，可以有效提升电网运营商在电力供需两端的管理优化能力，并维持日益复杂的智能电网系统的安全稳定运行[4]。随着具备“多表合一”能力的新型用能采集系统推广，电网企业在记录用电信息的同时可以便捷地获取用户的用水、用气等其他用能数据。居民用户的各类用能数据呈现高度的相关性，这些用电数据之外的能耗信息有助于更精准全面地刻画用户的用能特性[5-6]。

用能特性分析不仅有助于电网企业的优化运营，同时也为自来水与天然气等供应商的运营调度提供了重要参考，便于运营商之间的协同调度。针对“多表合一”背景下的新型用能特性分析问题，本文以电力与燃气消费数据为例，通过层次聚类与自组织映射（self organized maps，SOM）聚类算法分别刻画与挖掘了高耗能地区，完成了基于综合能源计量数据的区域用能特性分析。

1 聚类方法

聚类是一类典型的无监督机器学习方法[7-11]。在电力研究领域中，聚类技术已经被较多地应用在用户负载特征分布描述问题中，而这一问题对于电力服务和管理有重要意义。在实际研究中，具体的聚类方式选择取决于可用数据本身的特征以及对生成聚类的要求。常用的聚类算法如下。

（1）K-均值聚类根据样本点之间的几何距离迭代地将相近的样本点划分为同一类别，是一种距离聚类算法。其目标函数J为

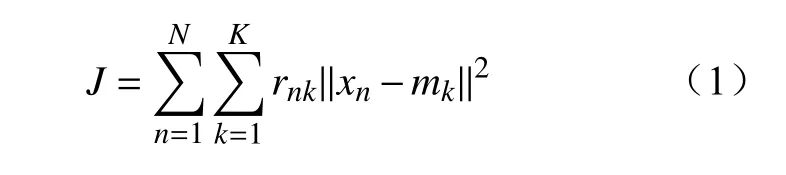
式中：xn为第n个样本；mk为第k个聚类中心；N为样本总数；K为聚类中心总数；rnk为指示变量，若样本xn被划分到mk所代表的类别，则rnk为1，否则为0。

（2）模糊C-均值聚类可以视为“软”分类版本的K-均值聚类。在模糊C-均值聚类中，一个样本点可以被同时划分到多个聚类簇中，此时指示变量由隶属度代替，该值表示样本xn属于mk所代表类别的概率。

（3）层次聚类可不断地将数据集中最相近的两个样本合并为一个样本，直到所有样本都被合并。层次聚类最终会将所有样本组织为一棵聚类树，每个样本占据聚类树的一个叶子结点[12]。

（4）SOM聚类是一种神经网络型的聚类算法，来源于自组织学习思想。自组织映射通过神经网络的权值变化来表现样本的归类过程，可以用于无法指定合适初始聚类中心的情形[13-16]。

在这些常见的聚类算法中，K-均值聚类与模糊C-均值聚类都需要预先设置类别数量，因此并不适合用能数据等模式较为复杂的情况。根据上述分析，本文基于层次聚类与SOM聚类进行用能特性分析，从而进一步体现原始数据的特征。

2 用能特性的层次聚类分析

本文采集某地区19个城市的16种类型建筑在每小时内的用能信息，包括商业建筑与住宅建筑。每个城市都关联多个数据文件，本文主要使用用电与燃气消耗数据，以便进一步探索不同用能数据的分析方法。

在聚类过程中，使用距离d刻画两个城市x与y之间用电数据的距离，即

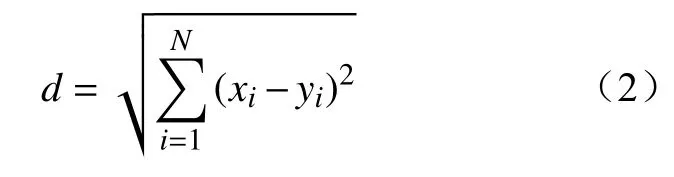
式中：xi、yi分别为第i小时城市x、y的负载水平。

本文从城际与城内两个方面对用户的用能数据进行层次聚类分析。其中城际分析关注用能特性在空间上的分布，城内分析则关注城市居民用能的时间分布特征。

2.1 城际分析

数据集中19个城市用电数据层次聚类结果如图1所示。在图1中，纵轴表示所有二元聚类中两个样本的相对相异度。相对相异度的具体算法可以参考文献[17-18]，其数值越小表示相似程度越高，也就是可以越早被聚类为一组。从图1可以看出，19个城市在用电行为特征上大致可以分为红色与蓝色群集，城市内部相似性较高，城市之间差异较大，相异度接近80%。与此同时，蓝色群集所有城市之间的相似程度都较高且十分接近，在用电管理政策制定时，可作为一个超大型城市处理。红色群集仅有2号与10号城市相似性较高，其用电特征模型更为多样化。

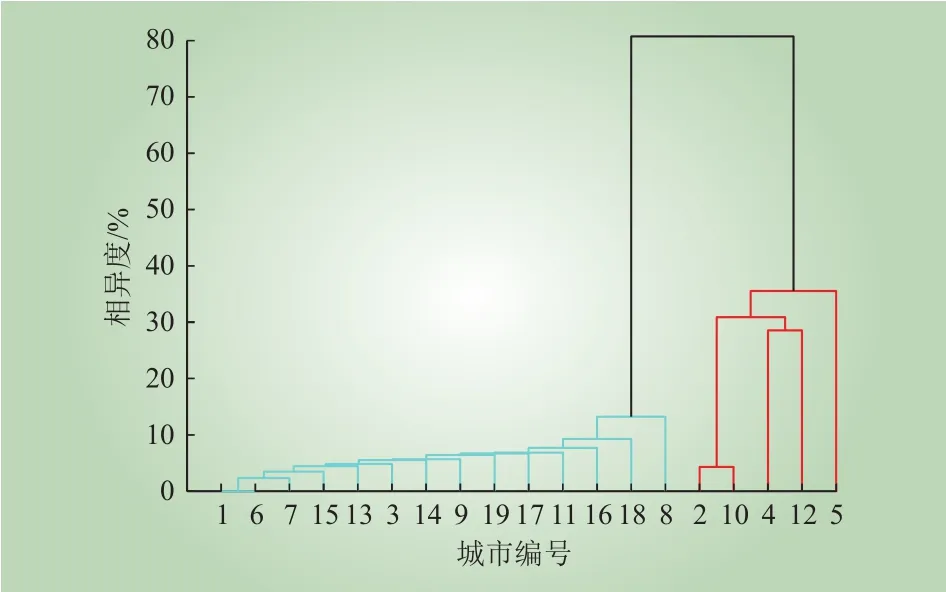
图1 用电数据城际层次聚类Fig. 1 Inter-city hierarchical clustering for power consumption

为进一步说明在引入燃气消耗数据后，各城市的层次聚类结果，在计算聚类空间中各城市所对应点的距离时，使用拼接用电量构成的向量与用气量构成的向量的方式得到用能数据城际层次聚类如图2所示。本文以相异度30%为阈值，19个城市依然可以分为红色与蓝色两个群集，且具体分组情况与图1相似。因此，在结合燃气数据后，城市之间的相似程度受到了影响，但用能行为特征分布依然保持稳定。

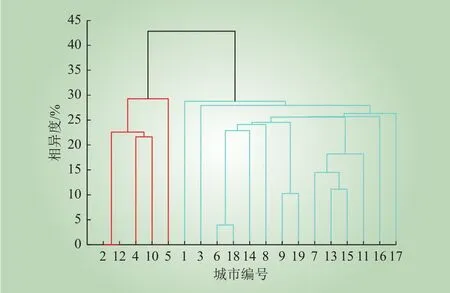
图2 用能数据城际层次聚类Fig. 2 Inter-city hierarchical clustering for energy consumption

2.2 城内分析

与城际分析不同，城内分析注重城市用能行为在时间上的分布情况。具体地，将城市中每小时的用能信息作为样本进行聚类，故城内分析结果可以有效地指导电力企业在用能峰谷期的运营调度。以城市1为例，对某天的用电数据进行层次聚类可以得到城市1的用电数据城内层次聚类结果如图3所示。从图3可以看出，全天用电量能被清晰地划分为2个阶段。

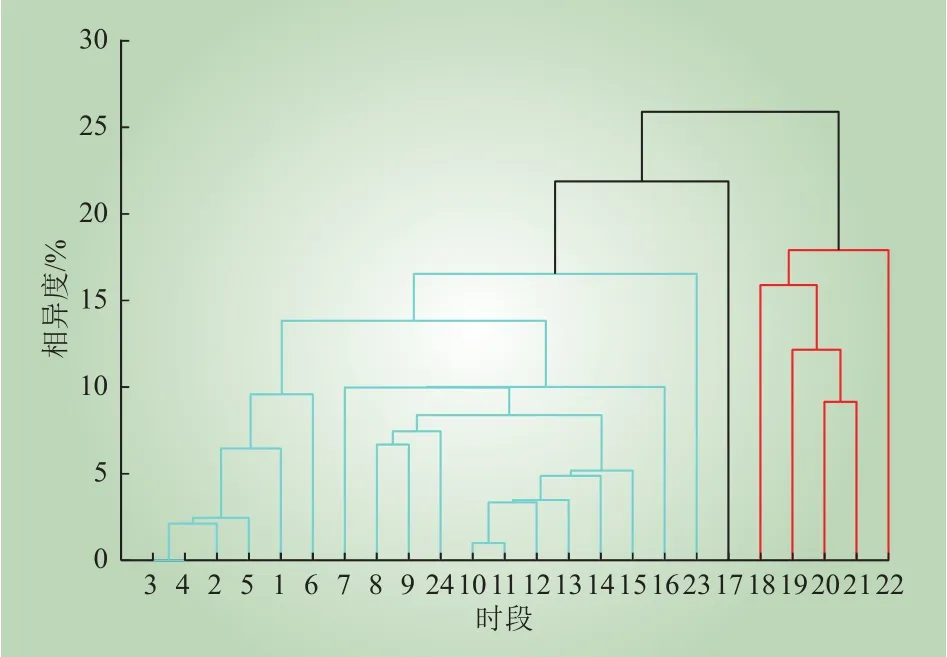
图3 城市1的用电数据城内层次聚类Fig. 3 Intra-city hierarchical clustering for power consumption of City 1

基于文献[19-21]的方法，可以求出城市1每天聚类结果的共性分类相关系数（cophenetic correlation coefficient，CPCC）矩阵，该系数体现了层次聚类结果对样本相异程度的表现能力，其值越接近1说明聚类模型表现力越强。本文通过Matlab软件包中的cophenetic函数直接计算CPCC的值，通过分析发现用电特性在每小时时段上的分布与具体日期关系较小，这也说明聚类分析可以更好地挖掘峰谷模式，而不会受具体负载水平的影响。城内时间分布聚类方法也可以用在其他种类的用能特性分析问题上。

城市1天然气消耗量的层次聚类结果如图4所示。结合图3和图4可以看出，用气数据与用电数据在时间上的分布表现出一定的相关性，且存在部分差异。

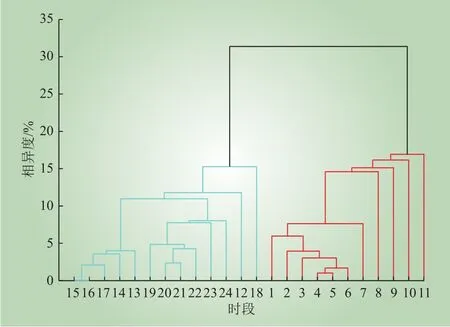
图4 城市1的用气数据城内层次聚类Fig. 4 Intra-city hierarchical clustering for gas consumption of City 1

3 用能特性的SOM聚类分析

本文使用SOM聚类对用能数据进行深入分析。SOM聚类是基于大量神经元自组织的竞争-合作过程[22-26]。若输入特征空间为D维，输入单元i与神经元的连接权重为wi，则判别函数f为各神经元的输入值构成的向量与各神经元的连接权重构成的向量的平方欧氏距离，即

在竞争过程中，使权值向量最接近输入特征向量的神经元作为胜利者，从而使连续的输入空间映射到一个神经元上。合作过程能够反映输入信息在网络中的扩散程度[27-31]。当某个神经元在竞争过程中获胜后，选择一部分相邻的其他神经元，按指数衰减规律将输入特征进行映射，并重新开始竞争过程。反复执行这两个步骤直至胜利的神经元不再变化，从而该神经元就代表了输入特征所归属的聚类。

本文以城市为单位，将19个城市一年数据作为输入进行比较，将全年数据作为输入。网络规模为6×4个神经元，每小时对应一个神经元。

网络神经元中各城市的权值如图5所示。从图5可以看出，19个城市被清晰地分为高耗能组与低耗能组，分别对应层次聚类中的红色群集与蓝色群集。综上所述，相比简单的层次聚类，SOM方法的优势在于不仅能有效地发现群集，还可以深入揭示不同群集的数值特征。

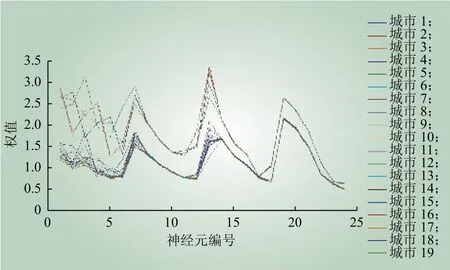
图5 网络神经元中各城市的权值Fig. 5 Weights per neuron of cities in SOM network

4 结语

本文研究了聚类方法与“多表合一”计量数据在区域用户用能时空分布特性分析问题中的应用。以真实的城市用电与燃气数据进行实验，基于层次聚类与自组织映射网络方法刻画用能特征分布，所提方法有助于电力运营商制定调度和规划方案。与此同时，本文方法可以发现用能特性相似的用户群体，能够基于聚类方法定量分析群集的数值特征，对于综合能源计量数据分析与用能政策制定有一定参考意义。