让联想成为习惯 让解题更为自然——以一道三角形中的最值问题为例

周子晰，郭建华

(1.南京市第二十九中学高三(13)班，江苏南京，210036 2.南京市金陵中学，江苏南京，210005)

联想，是数学解题的一种基本能力，在数学解题中，联想指由某概念而引起其他相关的概念.在数学解题中，通过对问题多角度地分析可以引发学生广泛地联想，包括对新、旧知识的关联，数学三种语言(自然语言、图形语言、符号语言)之间的关联，以及在显性条件下探索隐性条件的过程中对数学思想方法等的联想.

三角形中的最值问题是一个难点，它不仅涉及到解三角形、三角函数、三角恒等变换等相关知识，而且在解题中渗透数形结合、转化与化归等多种数学思想.下面，通过一道试题的深入分析，谈谈联想在解题中的应用.

1 试题呈现

例1设△ABC的三个内角A，B，C的对边分别为a，b，c，若点G为△ABC的重心，且AG⊥BG，则cosC的最小值为.

分析：题目条件涉及到三角形重心的概念以及重心所满足的位置关系，所求结论是角C的余弦值.重心是求解问题的突破口，首先要联想与重心相关的性质，其次要将AG⊥BG转化为三角形的边、角关系，进而表达cosC，再结合向量、函数、不等式、平面几何、解析几何等知识求解.

2 思路探索

图1

思路1 联想余弦定理

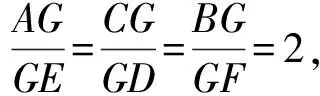
评注：解法1充分利用中线CD的长及∠ADC+∠BDC=π这一隐含条件，采用“算两次”的思想探寻三角形三边的关系；解法2结合重心的性质，采取“设而不求”的方法探寻三角形三边的关系.解法2的处理方式较为简捷.

思路2 联想“向量”

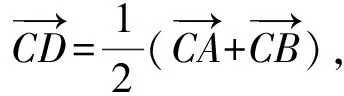
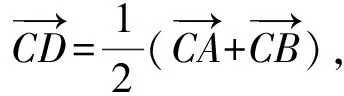
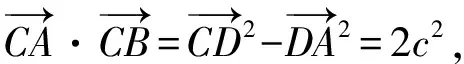
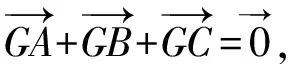
思路3 联想“圆”

该题以三角形为背景，结合要求解的目标cosC，思考如下问题：能否从平面几何的视角考虑问题?它涉及到哪些几何量?它们之间存在怎样的关联?还可以联想到哪些与之相关的几何量？自然联想到正弦定理和三角形的外接圆.

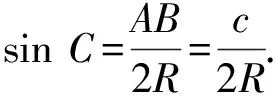
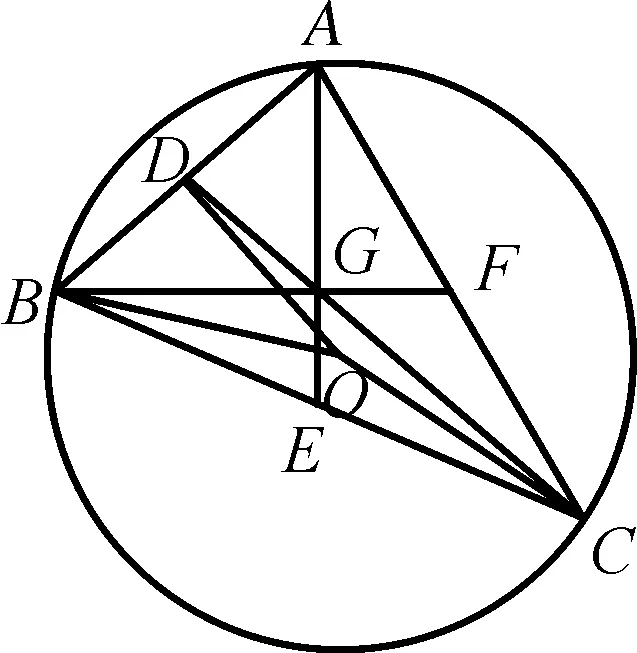
图2

思路4 联想“坐标系”

根据思路3的分析和求解，可以再作进一步的联想，由AG⊥BG，很容易联想到建坐标系求解，将几何问题转化为代数问题求解，合理地建立坐标系可以减少繁琐的运算.

图3

评注：用坐标法处理(根据解题的需要适当建立平面直角坐标系)很容易表达目标.采用“解析”法处理问题则让学生更容易着手分析和解决问题.以上两种想法有异曲同工之妙.对于填空题我们应该追求“小题小做，小题巧做”的目标，以上分析求解中均涉及到两个变量，可否将目标化为单变量问题?也可以作如下特殊化处理，即令n=-1，简化了表达的运算形式.

3 变式探究

例2设锐角△ABC的三个内角A，B，C的对边分别为a，b，c，若点G为△ABC的重心，且AG⊥BG，则cosC的取值范围为.

通过以上解题思路的探索，对原题设条件进行加强，思考两道题的区别和联系，新增加一个条件会为解题带来怎样的变化?会产生怎样的联想?让联想成为解题的一种习惯，让联想为解题思路的获得提供很多的可能.

思维的拓展离不开丰富的联想，联想为创造性解题提供了一把金钥匙.在处理典型问题时尽可能地从多个角度分析和思考，挖掘问题的各个方面，使得通过一道题，不仅让学生获得具体的解法，而且让学生体验问题解决过程中所渗透的数学思想和方法，从而沟通知识间的内在联系，深刻理解问题的本质.通过联想，让每一个“好题”变成一个充满无穷魅力的“世界”；通过联想，探究问题的纵横联系，将孤立的问题“串”起来，让学生的思维“活”起来，真正发挥解题的功能，发展学生的数学核心素养.