三维隔震结构摇摆动力模型及振动台试验验证

刘文光 李金乐 许浩 何文福

摘要：建立了三维隔震结构的平动⁃摇摆耦联动力分析模型，给出了结构动力方程，得到了三维隔震层的摇摆响应理论表达式，并进行了结构水平、竖向、摇摆频率比以及隔震层阻尼比等参数的影响分析，发现摇摆响应随水平、竖向、摇摆频率比的增大存在峰值区间，但总体上均呈减小趋势，且摇摆运动的激励频率由输入地震主频和水平运动频率共同控制。完成了三维隔震模型的振动台试验，对比验证了摇摆响应随竖向频率比的变化规律。最后进行了不同高宽比算例结构的地震响应分析，发现三维隔震结构的摇摆频率易接近摇摆激励主频造成共振，其摇摆响应随高宽比变化存在峰值区间，总体呈增大趋势。

关键词：三维隔震；摇摆响应；频率比；阻尼比；高宽比

中图分类号： TU352.1；TU311.3    文献标志码： A    文章编号：1004-4523（2022）05-1200-11

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.018

引言

基础隔震技术具有优异的减震效果，可显著提升结构抗震能力，自1994年洛杉矶 Northridge 地震以来已在世界范围内得到了广泛应用[1]。传统的抗震设计中重视水平地震作用，认为竖向地震作用不会对结构造成严重影响[2]。然而地震是一项复杂的三维运动，多次强震记录也显示，地震动竖向加速度峰值超过水平加速度峰值，竖向地震作用对结构的影响不容忽视[3⁃4]，因此对结构进行三维隔震设计是非常必要的。

国内外学者进行了大量三维隔震系统研发和结构分析理论研究。Lee 等[5]设计了一种由弹簧和楔形摩擦块组成的竖向隔震装置，通过楔形摩擦块将竖向荷载转化为水平荷载，从而起到竖向减震的效果。 Chen 等[6]提出了一种利用组合液压油缸的变刚度隔震装置，并在一大跨结构中验证了其减震效果。Walaa等[7]提出了以磁流变阻尼器为竖向元件的半主动三维隔震装置。国内也有学者设计了由铅芯橡胶支座和组合液压缸构成的竖向变刚度三维隔震装置，通过改变液压缸参与工作腔室的种类和数量实现竖向变刚度特性[8]。许浩等[9]基于铅芯橡胶隔震支座的组合提出一种斜向滑动摩擦三维隔震装置，并建立了该三维隔震支座的非平行恢复力模型。三维隔震设计的共同特点是隔震层具有较低的竖向刚度，从而延长竖向隔震周期以实现三维隔震。

三向地震作用下上部结构会对隔震层产生较大的倾覆力矩，隔震层易发生摇摆倾覆[10]，引起隔震支座的受拉超限；三维隔震结构由于竖向刚度低，抗倾覆能力弱，摇摆问题尤其突出[11]。熊世树等[12]建立了三维隔震框架结构多维地震反应的非线性分析模型及其运动方程，并提出了一种既能有效解决三维隔震支座竖向阻尼的难题，又可以有效抑制摇摆的三维隔震支座。杜永峰等[13]在建立隔震结构在双向地震激励下倾覆力矩时域响应动力分析模型的基础上，探讨了结构高宽比和结构基本周期等因素对隔震结构抗倾覆力矩与倾覆力矩比值的影响。官俊良等[14]对不同大高宽比基础隔震结构在不同正弦波作用下的倾覆反应做了研究，并且发现高宽比较大的刚体模型在相同输入条件下，倾覆反应反而比小高宽比模型低。王栋等[15]也对不同高宽比基础隔震结构在地震波作用下的倾覆响应做了振动台试验研究。祁皑等[16]对高层隔震结构多阶振型减震机理与倾覆问题做了深入研究。为减小隔震结构的摇摆倾覆效应，Kageyama等[17]提出了一种在密封空气弹簧内设置反向交叉钢丝绳的隔震装置，可实现结构平动时钢丝绳随之滑动，摇摆时钢丝绳受拉，从而产生摇摆抑制的效果。Kato 等[18]和Sawa等[19]采用液压油缸作为竖向隔震装置，通过将各个柱下的油缸连通而实现抗摇摆效果。颜学渊等[20]设计了一种碟形弹簧三维隔震抗倾覆支座，通过在上部橡胶支座内布置抗拉钢丝绳以及在圆筒上端设置内向翼缘竖向限位装置来阻碍竖向弹簧向上受拉，从而发挥抗摇摆/抗倾覆的功能。魏陆顺等[21]也设计了一种在竖向隔震层中安装重载滚动直线导轨副用于控制结构摇摆反应的装置，通过振动台试验证明其有较好的摇摆控制效果。

从目前的研究进展来看，对于隔震结构在三向地震作用下的摇摆倾覆问题还有待进一步研究，地震输入与结构的摇摆响应关系不明朗。为解决上述问题，本文提出了三维隔震结构平动⁃摇摆耦联简化分析模型，并建立其动力方程，得到了隔震层摇摆响应的理论解，进行了三维隔震结构水平、竖向、摇摆频率比及阻尼比等参数相关性分析，并对不同竖向频率比的三维隔震结构进行缩尺振动台动力试验，最后完成了不同高宽比结构的摇摆响应对比分析。

1 三维隔震摇摆分析理论

1.1  力学分析模型

三维隔震结构在三向地震动耦合作用下会产生三个方向的平动和转动，为简化分析，对模型做以下假定：

（1）仅考虑结构平面内的运动，地震作用下结构发生平移⁃摇摆耦联运动；

（2）将上部结构视为刚体，结构质量和刚度沿高度均匀分布，且质心位于结构高度中心；

（3）水平与竖向地震动简化为简谐激励，且认为其主频相同；

（4）隔震层刚度简化为等效线性刚度计算。

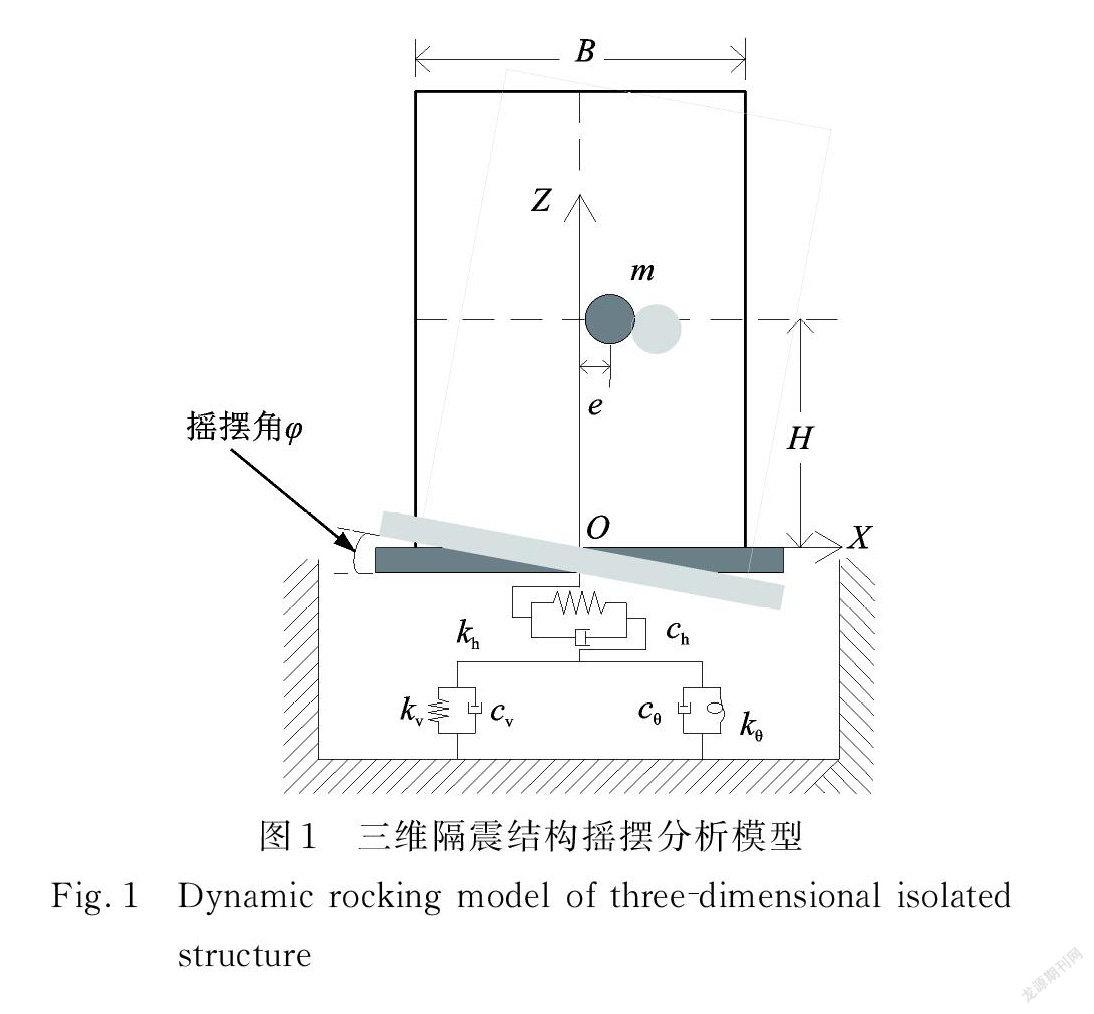
基于上述假定建立平面内平动⁃摇摆耦联运动力学模型如图1所示。该结构上部质量为 m，绕 O 点的转动惯量为 J，结构宽度为 B，质心高度为 H，偏心距为 e，隔震层水平、竖向、摇摆刚度和阻尼分别为kh，kv，kθ和ch，cv，cθ。

結构发生摇摆变形时隔震层刚心两边的竖向支座会分别产生方向相反的竖向位移抵抗其摇摆变形，因此摇摆刚度 kθ定义为隔震层发生单位摇摆角时的倾覆力矩，同时定义结构摇摆角φ值为隔震层两边竖向位移差与结构宽度 B 之比。

1.2  摇摆动力方程及解析解

由达朗贝尔原理可推导该系统动力方程如下式所示：

其中，水平输入荷载、竖向输入荷载分别为 F1 sin（θt）和 F2 sin（θt）。

用矩阵的形式可将式（1）表达为：

式（1），（2）中结构绕 O 点的转动惯量J=（ B2+ H 2） m/12+ mH 2+ me2。运动方程式（2）的特征方程满足：

令式（3）中系数行列式 K -ω2 M =0。由此可得到频率方程的三个根ω1（2），ω2（2）和ω3（2），结构三个不同频率ωi对应的振型为：

对式（1）进行正则坐标变换，即将位移 u 按振型展成如下形式：

式中  qi 为振型坐标。通过变换动力方程改写为：

忽略式（6）中的速度耦联项，把ϕTCϕ近似简化为对角阵，再利用振型的正交性有：

由式（7），可将式（6）转换为3个非耦联的单自由度体系的强迫振动方程：

式中

由于 Pi 为简谐荷载，在初始位移、速度均为零时，式（8）的解为：

式中ω Di 为有阻尼体系结构自振频率，ω Di =

再利用式（5）将三个振型反应叠加得到该体系水平、竖向、摇摆反应的理论解为：

同时，将式（1）中摇摆项运动方程移项为标准转动动力学方程为：

由式（13）右侧激励项可看出，结构的摇摆响应是由上部结构的水平/竖向惯性力引起的倾覆力矩造成的，摇摆激励的主频受结构水平运动频率、竖向运动频率及输入地震主频的影响。对于无水平偏心的结构，摇摆激励的频率则由结构水平运动频率和输入地震主频共同控制。

2 参数分析

由上述分析可知，影响三维隔震结构摇摆响应的参数有：结构的水平、竖向、摇摆频率和阻尼比等。为探讨各参数的定量影响关系，选取一模型算例，设定结构质量 m=5000 kg，宽度 B=10 m ，质心高度 H=10 m，偏心距为 e=1 m，水平、竖向刚度分别为kh =25152 N/m 、kv =308112 N/m，对应的水平、竖向和摇摆频率分别为0.35 Hz，1.25 Hz 和0.53 Hz 。参考Ⅱ类场地的第二组设计地震动，水平、竖向输入简谐荷载的频率取为2.5 Hz，加速度峰值为0.6g，以此组算例工况为基准，讨论不同水平、竖向、摇摆频率比（自振频率/输入荷载频率）和阻尼比对结构位移和摇摆响应的影响规律。

2.1  水平频率比、阻尼比分析

图2（ a ）为隔震层位移和摇摆角随水平频率比和阻尼比的变化曲线。水平向位移随水平频率比的增大呈减小趋势，在水平频率比为1时，由于水平向共振的影响，水平向位移达到峰值。摇摆角随水平频率比的增大整体略有减小趋势，在水平频率比为1时达到峰值，这是由于水平向共振引起结构倾覆力矩变大，导致摇摆角变大。竖向位移随水平频率比的变化基本保持不变，在水平频率比达到1时，水平向共振引起竖向位移也有所增大。随着结构水平阻尼比的增大，结构水平向位移和摇摆角均逐渐变小；而竖向位移在频率比为1左右时有所减小，之后基本保持不变。

2.2  竖向频率比、阻尼比分析

图2（b）为隔震层位移和摇摆角随竖向频率比和阻尼比的变化曲线。竖向位移随竖向频率比的增大呈变小趋势，在竖向频率比为1时，由于竖向共振，竖向位移达到峰值。摇摆角随竖向频率比增大整体呈变小趋势，在竖向频率比为1和1.2时出现两个峰值，其原因在于：竖向频率比为1时，竖向共振引起结构倾覆力矩变大，出现第一个摇摆角峰值；结构的摇摆刚度与竖向刚度相关，竖向频率的改变也会引起摇摆频率改变，当竖向频率比为1.2时结构的摇摆频率会与摇摆激励频率一致引起摇摆共振，出现第二个摇摆角峰值。水平向位移随着竖向频率比的增大基本保持不变，在竖向频率比为1和1.2时，由于摇摆角出现峰值导致水平向位移也有所变大。随着结构竖向阻尼比的增大，结构竖向位移和摇摆角均逐渐变小；而水平向位移在频率比为0.5～2时有所减小，之后基本保持不变。

2.3  摇摆频率比、阻尼比分析

结构的摇摆频率ω= ，保持结构质量不变，通过调整结构质心高度 H 改变高宽比，从而改变转动惯量 J 和摇摆频率，研究摇摆频率比对结构位移和摇摆角的影响。由于结构仅受到水平和竖向激励而无摇摆激励，所以此处摇摆频率比是指结构的摇摆自振频率与水平/竖向输入荷载频率之比。

图2（ c ）为隔震层位移和摇摆角随摇摆频率比和阻尼比的变化曲线。摇摆角随着摇摆频率比的增大整体呈变小趋势，在摇摆频率比为0.5左右时出现峰值。这是由于结构摇摆运动的激励频率由水平、竖向运动频率和输入荷载频率共同控制，而此处的频率比为结构的摇摆自振频率与（水平/竖向）输入荷载的频率比。当摇摆频率比为0.5左右时结构摇摆自振频率与摇摆激励频率一致，引起摇摆共振。水平向、竖向位移在频率比为0.4～2时受摇摆共振影响略有波动，之后基本保持不变。随着结构摇摆阻尼比的增大，结构摇摆角随阻尼比增加而逐渐变小；水平向、竖向位移在频率比为0.4～2时略有减小，之后基本保持不变。

3 振动台试验

3.1  试验模型设计

为进一步探究三维隔震结构的摇摆响应，进行了5层钢框架模型的振动台试验，模型相似关系如表1所示，振动台试验模型及量测方案如图3所示。

试验模型平面尺寸为1.6 m×0.8 m，总高度4.9 m，除首层外柱高均为0.95 m，隔震层设在模型柱底。钢框架梁柱采用 H 型钢焊接连接，各截面尺寸（高×宽×腹板厚度×翼缘厚度）分别为：梁截面：125 mm×60 mm×6 mm×8 mm；柱截面：100mm×100 mm×6 mm×8 mm；基础梁截面：250 mm×250 mm×9 mm×14 mm 。鋼框架重约1.8 t，模型底层和顶层配重1.2 t，标准层配重2.4 t，模型总重13.8 t 。隔震层采用4套斜向滑动型三维隔震支座模型[9]如图3（b）所示，该装置主要由水平支座、连接角块、斜向支座、限位装置和下承台组成，通过将铅芯橡胶支座斜置，使其在竖向地震作用下发生斜向往复变形和摩

擦滑块来回滑动，由此实现竖向滞回变形，水平支座则用来水平隔震，倾斜支座的竖向刚度随支座倾角的增大呈减小趋势。试验中每套三维支座中包括一只水平支座和两只倾斜支座，支座直径均为100 mm，倾斜角度分别为12°和15°，摩擦接触面为聚四氟乙烯和镜面不锈钢，试验时摩擦接触面涂抹润滑油，不同隔震支座的具体参数如表2所示。

3.2  量测系统及试验方案

为测量结构隔震层的摇摆响应及上部结构的位移响应，在隔震层设置位移传感器，由于传感器数量有限，上部结构跨层设置位移傳感器。为测量隔震层及上部结构的加速度响应，分别在隔震层及上部结构各层分别设置三向加速度传感器。隔震支座反力可由三向力传感器得到。传感器布置如图3（ c ）所示。

选用 El⁃ Centro 和 Taft 波作为输入地震动，具体信息如表3所示。

地震波按照时间相似系数压缩后按框架 XYZ 三方向输入，具体加载工况如表4所示。在对不同试验模型输入前，对模型进行白噪声扫频。此次试验对两种模型进行双向与三向输入地震加载，双向输入时峰值加速度比为1∶0.85（X ∶Z），三向输入时峰值加速度比为1∶0.85∶0.65（X ∶Y ∶Z）。倾斜支座的倾角为15°时，主向峰值分别设定为0.15g 和0.3g，此时隔震层发生了明显的摇摆变形。为确保试验安全性，对倾角为12°模型进行试验时，地震输入采用逐级递增方式，主向峰值分别为0.2g，0.3g，0.4g。

3.3  试验结果

3.3.1 加速度响应研究

加速度大小是分析结构动力响应的重要因素，由表5可得，振动台面峰值加速度与设计峰值基本吻合。采用三维隔震技术后，隔震层的加速度响应明显减小，其中水平减震率最大达到55%，竖向减震率达到61%。对比工况 T2和工况 T6，以及工况 T3和工况 T7，发现倾角15°模型的竖向隔震效果优于倾角12°模型，而水平隔震效果基本一致。

3.3.2 摇摆响应研究

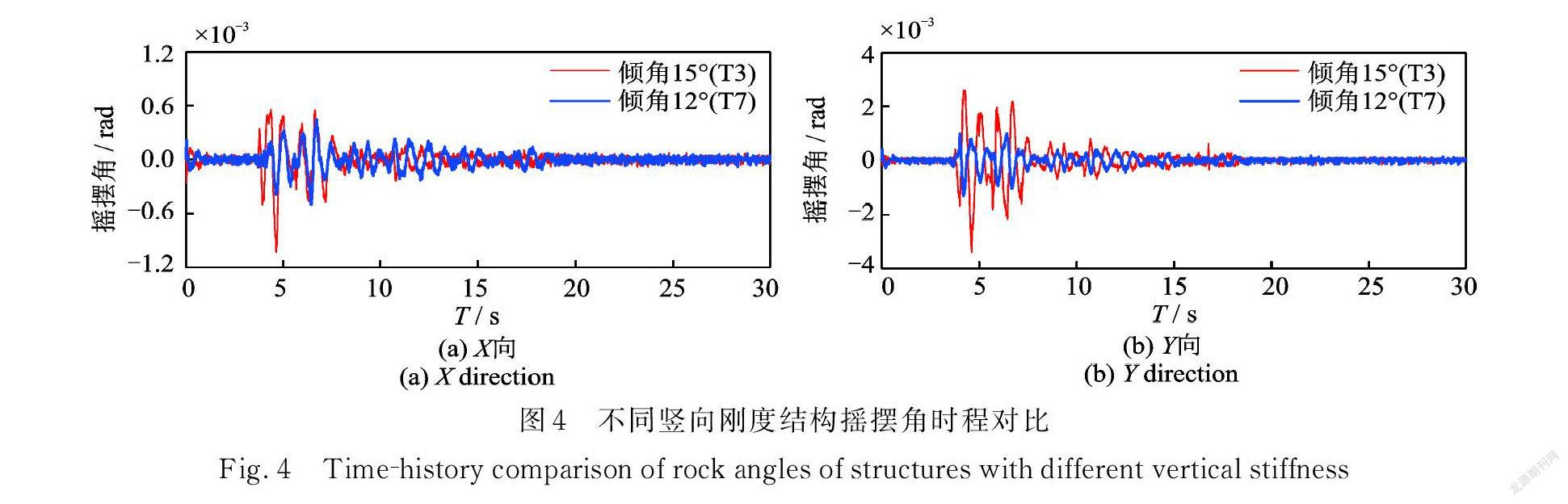
隔震层的摇摆响应是此次试验关注的重点，试验过程中观察到了隔震层发生了明显的摇摆变形，引起上部结构晃动。各工况下隔震层的摇摆变形如表5所示。选取除竖向刚度以外其余条件相同的试验工况（T3和 T7）进行比较，其摇摆角时程对比曲线如图4所示。

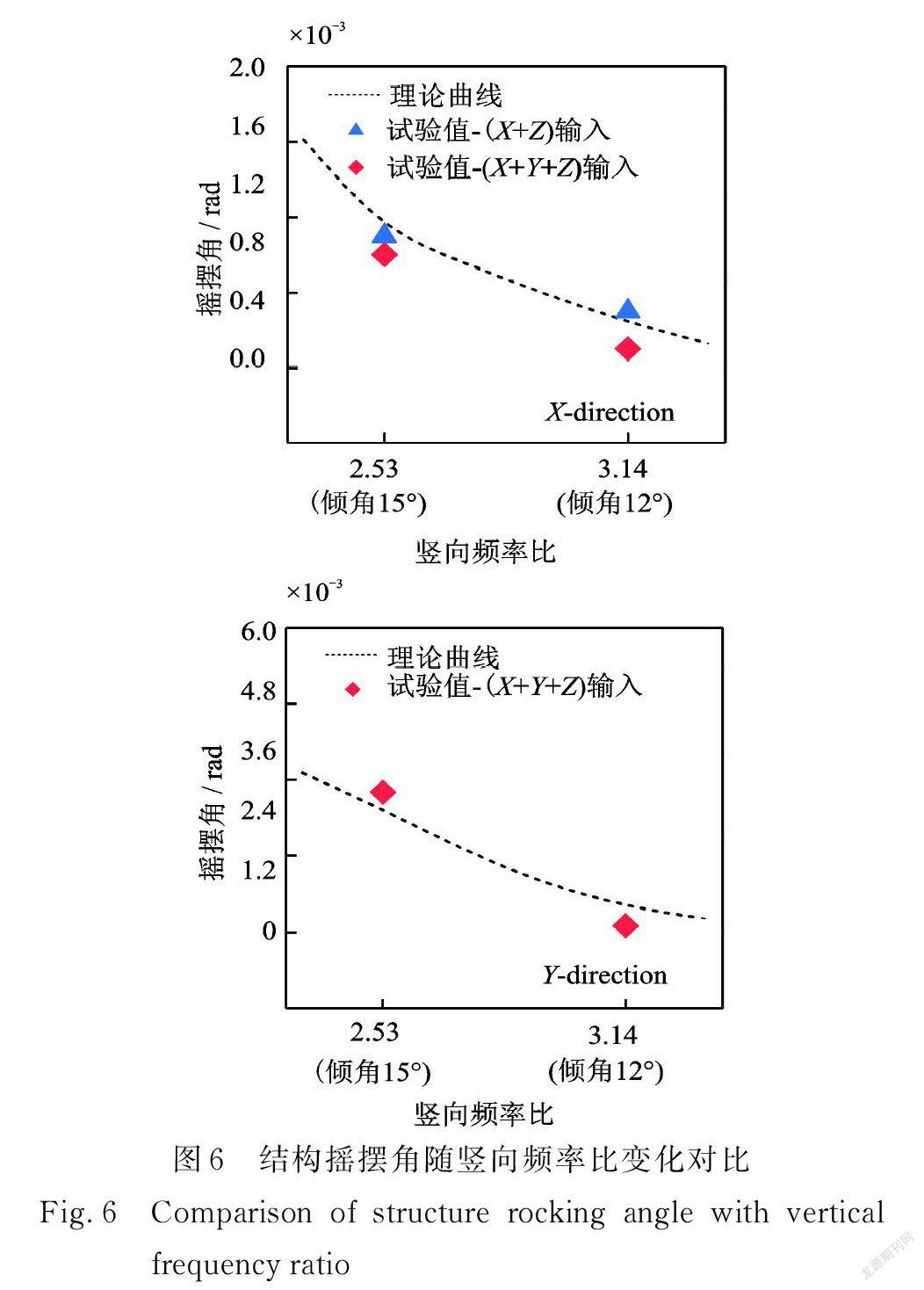
为验证摇摆响应随竖向频率比的变化规律，选取（T2和 T6、T3和 T7）两组竖向频率比下结构摇摆角与理论值进行对比。摇摆角理论值根据式（13）求得，计算时激励的频率为实际输入地震波的主频，支座刚度采用等效线性刚度，等效刚度值和阻尼比均由试验测得的滞回曲线得到，其中工况 T7下支座的滞回曲线如图5所示。摇摆角随竖向频率比的变化曲线与理论值对比如图6所示。结构的摇摆响应与理论值误差均小于25%，其中倾角12°的三维隔震层 X 向与 Y 向摇摆变形均小于倾角15°，其原因在于：随着竖向频率的增大，相应的竖向刚度也增大，结构所提供的摇摆刚度变大，因此隔震层摇摆变形减小，与理论研究趋势一致。

4 算例分析

4.1  分析模型

为进一步研究摇摆频率对结构摇摆响应的影响规律，选用高宽比分别为1～6的二维框架结构进行分析，不同高宽比结构的立面图如图7所示。

框架结构跨度为6 m，层高为2 m，框架柱截面尺寸为500 mm×500 mm，梁截面尺寸为600 mm×350 mm 。结构质量分布均匀，无水平偏心，对于不同高宽比结构通过调整结构每层的附加荷载，使总质量保持一致，均为101700 kg 。针对高宽比不同的结构，设计了水平隔震、三维隔震和非隔震三种类型的模型进行对比分析。

结构抗震设防烈度为8度，场地类别为Ⅱ类，设计地震分组为第二组。选取三条地震波：El⁃ Centro 波、Loma 波和 Taft 波作为地震激励，加速度峰值调整为70 Gal，相当于8度区多遇地震水平。水平向与竖向地震分量加速度比值按1∶0.85（X ∶Z）输入。

隔震设计目标按照《建筑抗震设计规范》，实现主体结构降一度目标。建立有限元模型进行分析，水平及三维隔震结构均采用2套隔震支座。水平隔震结构中，隔震层水平向采用Plastic⁃wen单元，性能为双线性滞回特性；竖向采用MultiLinear Elastic 单元，性能为拉压不等特性，其拉伸刚度为压缩刚度的1/8[22]。三维隔震结构隔震层水平向和竖向均采用Plastic⁃wen单元，性能为双线性滞回特性。单个支座的力学性能参数如表6所示。

4.2  分析结果

表7为不同类型结构随高宽比变化的动力特性。其中，非隔震结构的水平、竖向及摇摆频率均随高宽比的增大而减小，其摇摆频率远大于水平频率与地震激励主频；水平隔震结构随着高宽比的增大，结构的水平频率基本保持不变，竖向、摇摆频率呈变小趋势，其摇摆频率也始终大于水平频率与地震激励主频；三维隔震结构随着高宽比的增大，结构的水平、竖向频率基本保持不变，摇摆频率呈变小趋势。

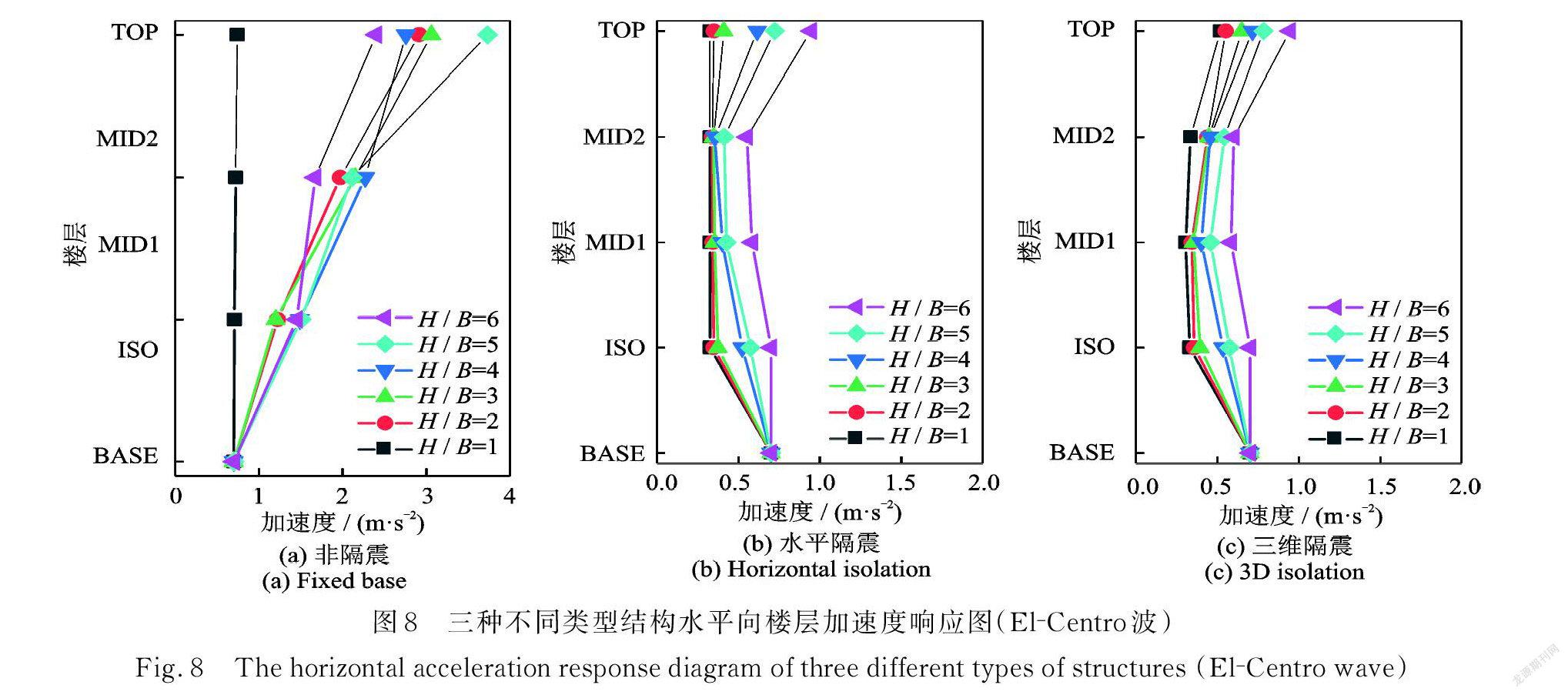
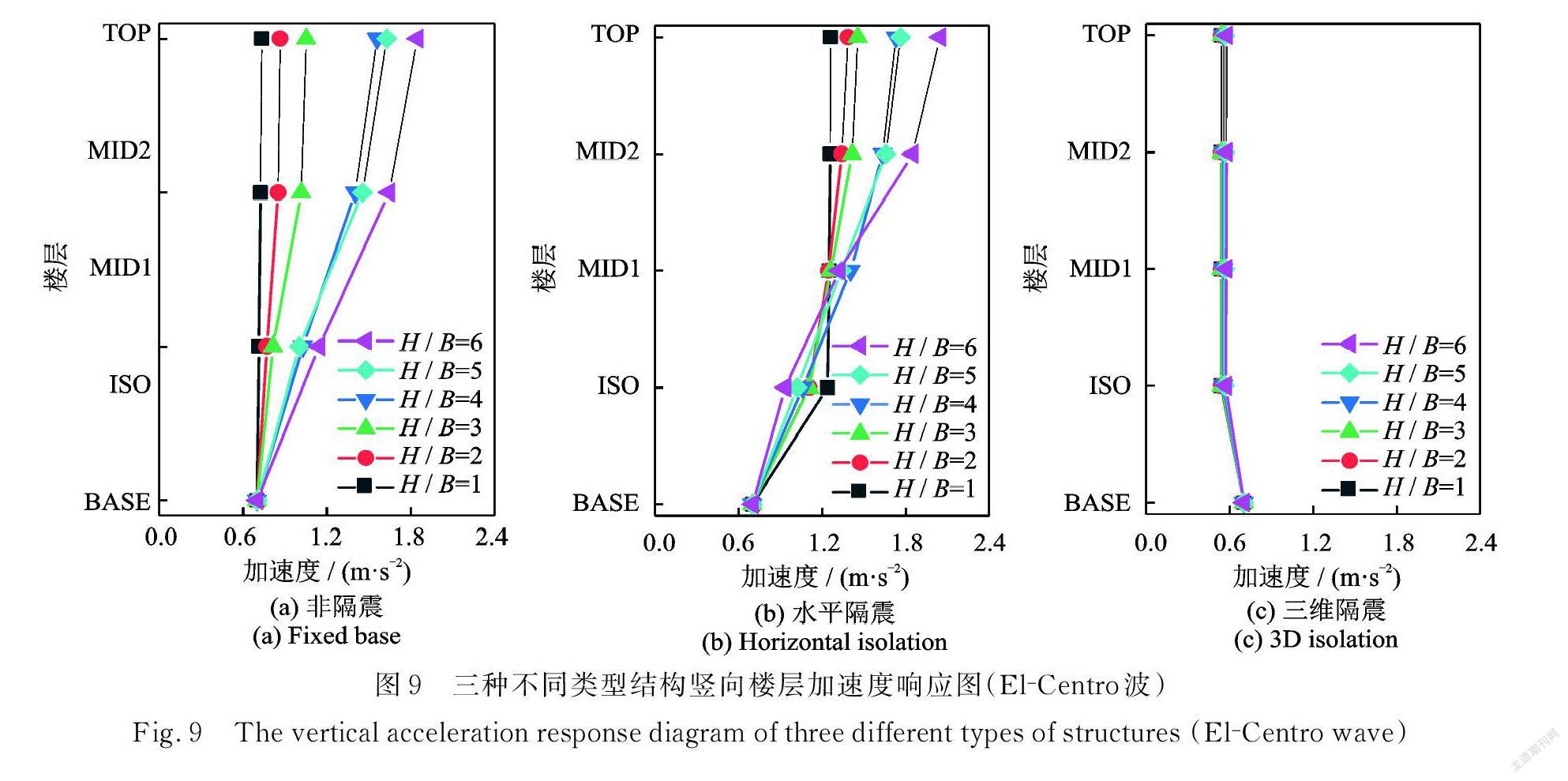
图8和9分别为不同类型结构在 El⁃ Centro 波作用下结构水平向、竖向楼层加速度响应图。水平和三维隔震结构水平向隔震效果相当，相比非隔震结构均显著降低；水平隔震结构的竖向加速度响应相比非隔震结构有所放大，三维隔震后结构竖向加速度相对于非隔震和水平隔震结构均有了明显减小。

图10为不同类型结构的摇摆角峰值随高宽比的变化趋势。其中，非隔震结构的摇摆角选取上部结构顶部两边的竖向位移差与结构宽度之比来表示，水平和三维隔震结构选取隔震层和上部结构两个部位的摇摆角进行研究。对于高宽比一致的结构，上部结构摇摆响应从大到小分别为三维隔震、非隔震、水平隔震结构。这是由于三维隔震结构的摇摆刚度相比水平隔震和非隔震结构都要小得多，因此摇摆响应最大；而非隔震结构虽然摇摆刚度很大，但其上部结构水平向加速度较大造成倾覆力矩远大于水平隔震结构，因此结构的摇摆角大于水平隔震结构。

由图10可知，非隔震结构的摇摆角峰值随高宽比的增大而增大。水平隔震结构隔震层和上部结构的摇摆角峰值均随高宽比的增大而增大，上部结构的摇摆角相比隔震层要大很多。三维隔震结构隔震层和上部结构的摇摆角峰值随高宽比增大均呈先增大后减小再增大的趋势，在高宽比 H/B=3～4之间存在峰值。这是由于摇摆的激励频率由地震激励主频和水平频率控制，在高宽比 H/B=3～4之间存在结构摇摆频率与摇摆激励频率一致的情况，引起结构摇摆共振。同时三维隔震结构由于隔震层的摇摆刚度较小，摇摆变形主要发生在隔震层，上部结构近似做刚体运動，因此上部结构的摇摆角相比隔震层仅略微变大。

隔震结构的摇摆变形无法完全避免，算例模型中三维隔震结构相比于水平隔震和非隔震结构，其摇摆频率较小，更接近摇摆激励主频从而导致共振。三维隔震层本身提供的抗摇摆刚度是有限的，因此需考虑增设抗摇摆装置提高隔震层摇摆刚度，增大摇摆频率，从而控制结构摇摆变形。

5 结论

本文建立了三维隔震结构的摇摆响应动力模型和理论解析式，并完成了振动台试验和算例分析，得到主要结论如下：

（1）建立了三维隔震结构的平移⁃摇摆耦联运动方程，通过振型分解给出了摇摆响应的理论表达式，发现无水平偏心的三维隔震结构摇摆运动的激励频率由输入地震主频和结构水平运动频率共同控制。

（2）进行了结构摇摆反应的参数影响水平分析，发现三维隔震结构摇摆响应随水平、竖向、摇摆频率比的增大存在峰值区间但总体上均呈减小趋势，随水平、竖向、摇摆阻尼比的增大均减小。

（3）完成了缩尺模型振动台试验，发现支座倾角15°模型的竖向隔震效果优于倾角12°模型，但摇摆响应大于倾角12°模型；随竖向频率比变化摇摆响应的试验值与理论值具有相同的变化规律，具体数值误差在25%以内。

（4）进行了不同高宽比算例结构的地震响应分析，发现三维隔震结构的摇摆响应随高宽比变化存在峰值区间但总体呈增大趋势，其摇摆频率较小易接近摇摆激励主频造成共振。

参考文献：

[1] 陈鹏，周颖，刘璐，等.带抗拉装置高层隔震结构振动台试验研究[ J ].建筑结构学报，2017，38（7）：120-128.

CHEN Peng，ZHOU Ying，LIU Lu，et al . Shaking ta⁃ ble test on high-rise isolated building with tension-resis⁃ tant devices[ J ]. Journal of Building  Structures ，2017，38（7）：120-128.

[2] 刘文光，余宏宝，IMAM MOUSTAFA I，等.倾斜旋转型三维隔震装置的力学模型和竖向性能试验研究[ J ].振动与冲击，2017，36（9）：68-73.

LIU Wenguang，YU Hongbao，IMAM MOUSTAFAI，et al . Tests for mechanical model of an inclined rota ⁃ tional three-dimensional seismic isolation device and its vertical  performance [ J ]. Journal  of  Vibration  and Shock，2017，36（9）：68-73.

[3] 党育，霍凯成.多层隔震结构的竖向地震作用研究[ J ].地震工程与工程振动，2010，30（4）：139-145.

DANG  Yu ， HUO  Kaicheng . Vertical  earthquake  re⁃ sponses of multi-storey isolated buildings[ J ]. Journal of Earthquake  and  Engineering Vibration ，2010，30（4）：139-145．

[4] 尚守平，王振，尹奋.新型三维隔震墩隔震单元参数设计研究[ J ].地震工程与工程振动，2017，37（4）：104-111.

SHANG Shouping，WANG Zhen，YIN Fen . Research on design of the element of seismic isolation  for a new three-dimensional  seismic  isolation  pier [ J ]. Journal  ofEarthquake  and  Engineering Vibration ，2017，37（4）：104-111.

[5]  Lee Y，Ji Y S，Han W，et al . Shaking table test of ver⁃tical  isolation device[ J ]. International Journal  of Envi⁃ ronmental Science & Development，2014，5（1）：5-7.

[6]  Chen Z，Ding Y，Shi Y，et al . A vertical isolation de ⁃vice  with  variable  stiffness  for  long-span  spatial  struc⁃ tures[ J ]. Soil  Dynamics  and  Earthquake  Engineering，2019，123：543-558.

[7]  Walaa E，Keri R，Sevki C，et al . Displacement veloci⁃ty-based control of a liquid spring-MR damper for verti⁃ calisolation[ J ]. Structural Control and Health Monitor⁃ ing，2019，26（7）：1545-2255.

[8] 陈兆涛，丁阳，石运东，等.大跨空间结构竖向变刚度三维隔震装置及其隔震性能研究[ J ].建筑结构学报，2019，40（10）：35-42.

CHEN  Zhaotao，DING  Yang ，SHI  Yundong，et  al . Research  on isolation performance of three-dimensional isolation device with vertical variable stiffness[ J ]. Jour⁃ nal of Building Structures，2019，40（10）：35-42.

[9] 许浩，刘文光，何文福，等.斜向滑动摩擦三维隔震装置的滞回模型及其隔震效果[ J ].建筑结构学报，2017，38（10）：123-130.

XU Hao，LIU Wenguang，HE Wenfu，et al . Research on hysteretic model and  isolation  effect of oblique slid⁃ ing  friction 3D  seismic  isolation  device [ J ]. Journal  of Building Structures，2017，38（10）：123-130.

[10]余欣欣.三维隔震结构的摇摆效应及控制策略[ D ].上海：上海大学，2019.

YU Xinxin . Rocking effect and control strategy of three dimensional isolated structure[ D ]. Shanghai：Shanghai University，2019.

[11]张龙飞，陶忠，潘文，等.导轨式抗拉橡胶支座力学性能研究[ J ].振动与冲击，2018，37（22）：122-127.

ZHANG Longfei，TAO Zhong，PAN Wen，et al . Me ⁃chanicalproperties  of rail-type  anti-tensile  rubber bear⁃ings [ J ]. Journal  of  Vibration  and  Shock ， 2018， 37（22）：122-127.

[12]熊世树，陈金凤，梁波，等.三维基础隔震结构多维地震反应的非线性分析[ J ].华中科技大学学报（自然科学版），2004，32（12）：81-84.

XiongShishu，Chen Jinfeng，Liang Bo，et al . Nonlin ⁃ ear analysis of multi-dimensional seismic response in 3D base isolated structure[ J ]. Journal of Huazhong Univer⁃ sity  of  Science & Technology （Nature  Science  Edi⁃ tion），2004，32（12）：81-84.

[13]杜永峰，李慧.双向地震激励下隔震结构抗倾覆特性的数值分析[ J ].计算机辅助工程，2011，20（1）：42-46.

DU Yongfeng，LI Hui . Numerical analysis on overturn⁃ ing resistant property of seismic isolated building subject to  bi-directional  earthquake  excitation [ J ]. Computer Aided Engineering，2011，20（1）：42-46.

[14]官俊良，程蓓，鄧烜.大高宽比刚体模型倾覆反应振动台试验研究[ J ].四川建筑科学研究，2017，43（6）：79-83.

GUAN  Junliang，CHENG  Bei，DENG  Xuan . Experi⁃ mental studies  on  overturning behaviors  of rigid bodies with large aspect ratio under shaking table tests[ J ]. Si⁃ chuan Building Science，2017，43（6）：79-83.

[15]王栋，吕西林，刘中坡.不同高宽比基础隔震高层结构振动台试验研究及对比分析[ J ].振动与冲击，2015，34（16）：109-118.

Wang Dong，LüXilin，Liu Zhongpo . Shaking table test and comparison analysis for base-isolated high-rise build⁃ ings with different aspect ratios[ J ]. Journal of Vibration and Shock，2015，34（16）：109-118.

[16]祁皑，徐翔.高层隔震结构多阶振型减震机理与倾覆问题研究[ J ].振动工程学报，2013，26（4）：487-492.

QI Ai，XU Xiang . Research on multi-modal damping ef⁃fect and overturning problem of high-rise isolated build⁃ings [ J ]. Journal  of  Vibration  Engineering ，2013，26（4）：487-492.

[17] Kageyama M，Hino Y，Moro S . Study on three-dimen⁃sional seismic isolation system for next generation nucle⁃ ar power plant：independent cable reinforced rolling-seal air  spring [C] Proceedings  of  ASME  Conference  on ASME/JSME 2004 Pressure Vessels  and Piping  Con⁃ ference .2004：49-56.

[18] Kato A，Umeki K，Morishita  M ，et  al . A  large  scaleongoing R &D project on three-dimensional seismic iso⁃ lation for FBR in Japan[C] Proceedings of ASME 2002 Pressure Vessels and Piping Conference .2002：1-9.

[19] Sawa N，Kajii S，Umeki K . Study on 3D seismic isola⁃tion applied to advanced power reactor：using hydraulic cylinder ：No .1[C] Dynamics and Design Conference：機械力学·計測制御講演論文集. The Japan Society of Mechanical Engineers，2002.

[20]颜学渊，张永山，王焕定，等.三维隔震抗倾覆结构振动台试验[ J ].工程力学，2010，27（5）：91-96.

YAN  Xue-yuan ，ZHANG  Yong-shan，WANG  Huan- ding ， et  al . Shaking  table  test  for  the  structure  with three-dimensional base isolation and overturn resistance devices [ J ]. Engineering  Mechanics ， 2010， 27（5）：91-96.

[21]魏陆顺，刘雷斐，梁欢文.三维隔震振动台试验研究[ J ].土木工程学报，2014，47（3）：33-38.

WEI Lushun，Liu Leifei，Liang Huanwen . Experimen⁃ tal study on three-dimensional seismic isolation[ J ]. Chi⁃ na Civil Engineering Journal，2014，47（3）：33-38.

[22]罗佳润，马玉宏，沈朝勇.隔震设计中橡胶隔震支座拉压刚度取值的研究[ J ].地震工程与工程振动，2013，33（5）：232-240.

LUO Jiarun，MA Yuhong，SHEN Chaoyong . Research on the ratio of tensile and compressive stiffness of rubber isolators in the isolation design[J ]. Journal of Earthquake and Engineering Vibration，2013，33（5）：232-240.

Rocking dynamic model of three -dimensional isolation structure and validation of shaking table tests

LIU Wen-guang1，2，LI Jin-le1，XU Hao1，2，HE Wen-fu1，2

（1.Department of Civil Engineering，Shanghai University，Shanghai 200444，China；

2. Seismic Isolation & Mitigation Control Center of Nuclear Plant，Shanghai University，Shanghai 200444，China）

Abstract： In this paper，a translational-rocking coupling dynamic analysis model of three-dimensional seismic isolation structure is established and its dynamic equation is given . The theoretical expression of the rocking response of the isolation layer is obtained . The correlation analysis of parameters such as horizontal，vertical，rocking frequency ratio and damping ratio of the isolation layer is carried out . It is found that the rocking response has a peak interval with the increase of the horizontal，vertical，and rocking fre? quency ratios，but generally shows a decreasing trend，and the excitation frequency of the rocking motion is controlled by the input seismic frequency and horizontal motion frequency . The shaking table test of the three-dimensional seismic isolation model is con⁃ ducted，and the law of the rocking response changing with the vertical frequency ratio is compared and verified . The seismic re ⁃ sponse analysis of the structure with different aspect ratios is carried out . It is found that the rocking frequency of the three-dimen⁃ sional seismic isolation structure is close to the rocking excitation frequency and causes resonance . The rocking response has a peak interval with the change of the aspect ratio，but the overall trend is increasing .

Key words ： three-dimensional isolation；rocking response；frequency ratio；damping ratio；aspect ratio

作者简介：刘文光（1968—），男，教授。电话：13701888336；E-mail：liuwg@aliyun .com。

通讯作者：许浩（1991—），男，助理研究员。电话：18616252793；E-mail：xuhaoxy08@shu .edu .cn。