fGn激励下非线性系统近似方法适用性的解析分析

邓茂林 朱位秋

摘要：由于受分数高斯噪声（fGn）激励的非线性系统响应不再具有马尔科夫性，基于扩散过程的理论方法不能直接用于研究此类问题。作为近似方法，宽带噪声激励的拟哈密顿系统随机平均法已经被用于解决此类问题。虽然，该理论方法在响应预测和可靠性分析方面取得了较好的效果，但是到目前为止还没有做过对近似方法的误差和适用性的解析分析。在本研究中，将近似方法用于分析fGn激励下的单自由度非线性系统，得到了系统响应的近似解析解，再结合已报道的精确解析解，用渐近分析的方法进行了误差分析，从而对近似方法的适用性进行了论证，为将来能够进一步扩展近似方法的应用提供了理论依据。

关键词：非线性系统；宽带噪声；分数高斯噪声；拟哈密顿系统随机平均法

中图分类号： O324    文献标志码： A    文章编号：1004-4523（2022）05-1076-08

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.005

引言

在随机动力学的理论研究和随机振动相关的应用研究中，高斯白噪声得到了非常广泛的应用，究其原因，一方面是因为高斯白噪声是许多实际噪声的良好的数学模型；另一方面是因为与高斯白噪声相关的数学理论已经发展得非常成熟[1⁃2]，受高斯白噪声激励的线性系统已经能够得到解析解。至于受高斯白噪声激励的非线性系统，根据系统响应过程的马尔科夫性，可以应用基于扩散过程的理论方法进行研究，其中就包括哈密顿理论体系框架内的非线性随机动力学的系列理论方法[3⁃4]。近年来，随着分数阶微积分应用研究的深入，自然界和工程界中的分数高斯噪声（fGn）受到越来越多的关注，并被引入到随机动力学中[5⁃6]。

fGn是一类具有特殊相关结构与谱密度的高斯色噪声，它的特点是具有长相关性[7⁃8]，受fGn激励的系统响应不是马尔科夫过程。根据相应的随机平均原理[9⁃11]，发展了fGn激励的拟哈密顿系统随机平均法[12⁃13]，导出了系统响应满足的分数阶伊藤随机微分方程。由于与分数布朗运动相关的随机微分方程理论尚在发展之中[14⁃15]，目前无法解析地预测系统响应，只能通过对分数阶伊藤随机微分方程做数值模拟得到系统的响应，因此，发展近似的理论方法就显得尤为重要。一种已被应用的近似方法就是宽带噪声激励下拟可积哈密顿系统随机平均法，该法已经被成功应用于fGn激励下多自由度强非线性系统的响应预测和可靠性分析[16⁃17]。近似方法利用了fGn的功率谱在频率远离零点的范围内比较平坦的特点，fGn過程具有局部宽带的特性。由于高维 FPK 方程难以得到解析解，对该近似方法的适用性分析也只能是通过数值解和模拟结果的比较来进行，尚缺乏严谨的理论分析。本研究正是想弥补这个缺陷，通过把宽带噪声激励下拟可积哈密顿系统随机平均法应用于一个典型的受fGn激励的单自由度非线性系统，得到了系统响应的近似解析解，再通过与已报道的精确解析解相比较[18]，用渐近分析的方法进行了误差分析，论证了近似方法的适用性。这将使得近似方法在将来应用于fGn激励的多自由度强非线性系统稳定性与控制等更多更深入的研究中有坚实可信的理论依据。

1  fGn激励下单自由度非线性系统的响应

宽带噪声激励下拟可积哈密顿系统随机平均法适用于研究多自由度强非线性系统[3，19]，但是多自由度强非线性系统往往含有太多的非线性参数，且系统响应一般没有解析解，不便于对理论方法的适用性和误差进行解析的分析。此处考虑如下受fGn激励的单自由度非线性系统：

其中仅有参数 k 起着量化系统非线性强弱的作用；噪声 W （ t ）即是fGn，它具有如下自相关函数 R（τ）和功率谱密度 S（ω）[5，7⁃8]：

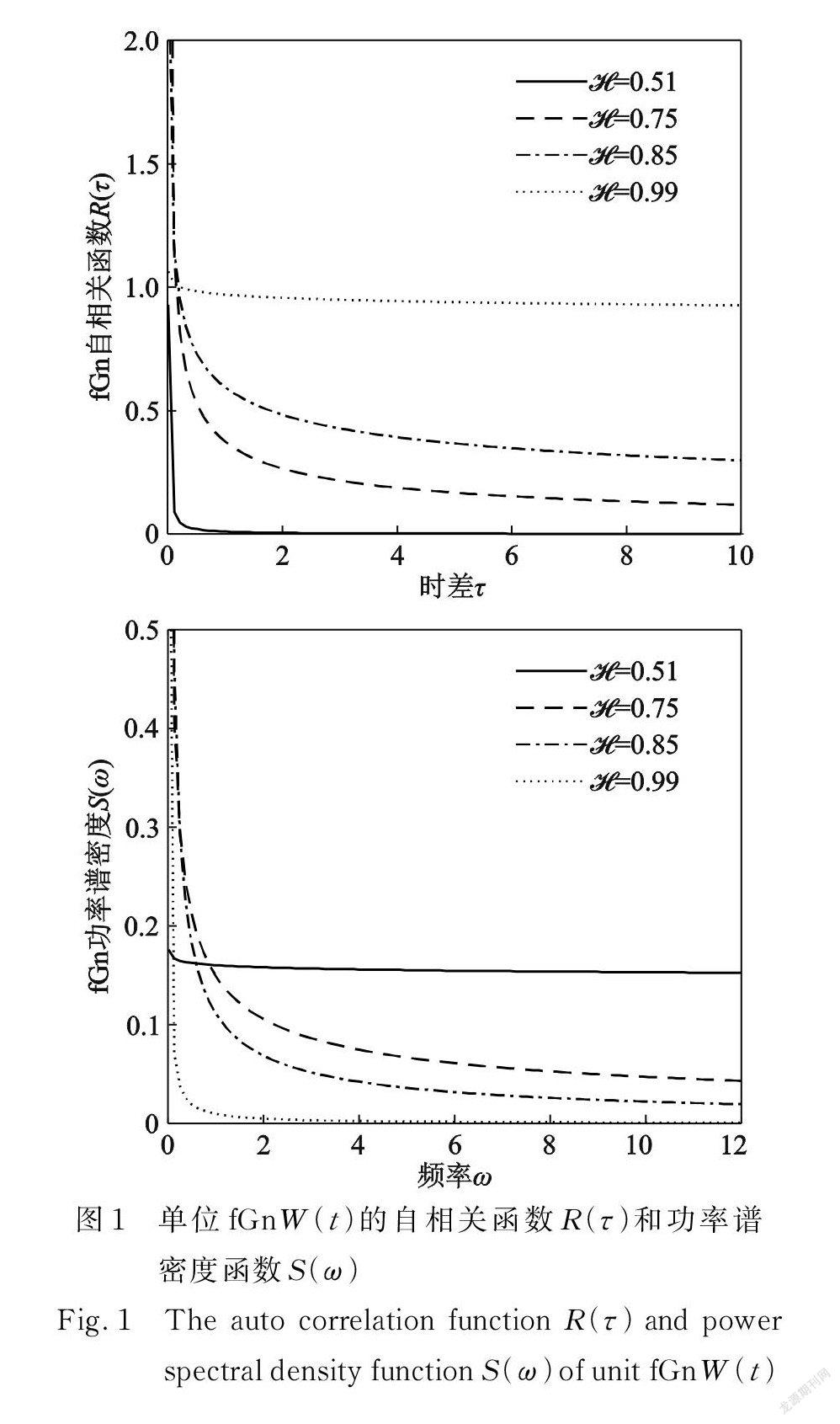
式中  2D 为噪声 W （ t ）的强度，当 D =0.5时， W （ t ）为单位fGn；ℋ为 Hurst 系数，它决定了fGn的性质。当 0<ℋ<时，fGn没有传统意义上的功率谱，不能作为实际工程振动中激励力的模型[5]。图 1显示了<ℋ<1时单位fGn的相关函数 R（τ）和功率谱 S （ω），当ℋ= 或ℋ=1时，式（2）不能直接计算，可采用以下极限形式：

可见，当ℋ→时，fGn的功率谱密度趋于常数，自相关函数趋于δ函数，这对应于高斯白噪声过程；当ℋ→1时，fGn功率谱密度趋于δ函数、而自相关函数趋于常数，这对应于高斯分布的随机变量；当<ℋ<1时，fGn是介于上述两者之间的有色高斯噪声，其最重要的性质就是当前噪声值与历史噪声值有着长相关性（又称长记忆性）[5，8]。

系统（1）的哈密顿函数 H（ X，Ẋ ） 也是系统的总能量函数，它可以表示为：

其中：

假定系统（1）的退化的保守系统在平衡点附近具有周期解，在弱激励和弱阻尼的条件下，可假定系统（1）的响应具有如下随机周期解的形式：

式（6）中的振幅 A 是哈密顿量 H 的确定性函数，v 是瞬时频率，它与哈密顿量 H 和相角Φ之间的关系可由式（4）和（6）推导得：

上式表明，v 是Φ的偶函数，可以展开成以下傅里叶级数：

即可得平均频率 （ H ）=，称其为非线性系统的主频率，并可表示成以下级数形式：

上式表明主频率位于退化线性系统的频率ω n 附近，因受非线性参数 k 的影响而有所偏离，且在振动过程中，主频率随系统能量 H 的变化而变化，在以后做平均运算的时候将用到以下近似关系：

式（6）可被视为从系统（1）运动状态 X（ t ），Ẋ （ t ）到 H（ t ），Θ（ t ）的变换，据此系统（1）可变换为以下等效的运动方程：

如前所述，受fGn激励的系统（1）的响应不是马尔科夫过程，但是考虑到对系统响应起主要作用的是系统主频率及其倍数频率附近的噪声成分，当这部分噪声具有宽带性质时，可应用宽带噪声激励下拟可积哈密顿系统随机平均法[19]。系统哈密顿过程 H （ t ）收敛于马尔科夫扩散过程，受如下平均后的伊藤随机微分方程支配[20]：

式中  B （ t ）是单位布朗运动过程（或称维纳过程），漂移系数 a （ H ）和扩散系数σ2（ H ）可按下式得到：

式中⋅ t 表示对时间 t 的平均，它可以用对相角Φ

为得到上述 FPK 方程中 a （ H ）和σ2（ H ）两系数的显式，可先把 F（ H ），G（ H ），G（Θ）展开成关于Φ的傅里叶级数，再对τ积分和对Φ进行平均，最终得两系数为：

稳态 FPK 方程（15）可被整理成伯努利型微分方程，并有如下形式的解[3]：

式中  C 为归一化常数。从式（16）可见，fGn对系统响应的贡献是通过 S（），S （3），S （5） …等功率谱密度值来实现。只要这些频率附近的功率谱密度缓慢变化，fGn就可以被近似为宽带噪声。

为了分析非线性参数 k 对系统响应的影响，可将式（17）表示成如下级数形式：

式中  S = S（ω n ），S '= S '（ω n ），S ″= S ″（ω n ），符号“'”和“''”分别表示一次和二次导数。从式（18）可知，当系统非线性较弱时，可仅取 k 的一次项，响应 p （ H ） 只受谱密度值 S（ω n ）及其导数 S '（ω n ）的影响；当系统非线性强一些时，可取到 k 的二次项，影响 p （ H ） 的因素多了 S（3ω n ）和二阶导数 S ″（ω n ），随着系统非线性增强，影响 p （ H ）的因素将包括更高倍频处的谱密度值和谱密度的更高阶导数。

概率密度 p （ H ）也可表示成如下 H 的无穷阶矩的形式：

更多系统响应的统计特性可以从 p （ H ）导得，比如系统位移 X 的各阶矩：

用式（19）中的 E [ H n ]或式（20）中的 E [ X 2n ]来分析非线性参数 k 对系统响应的影响，结论与前述以式（18）中的 p （ H ）来分析的结果相同，随着系统非线性增强，影响系统响应的将包括更高倍频处的谱密度值和谱密度的更高阶导数。

2 fGn激励下单自由度线性系统的响应

当非线性参数 k =0时，系统（1）退化为以下fGn激励的单自由度线性系统：

应用线性随机振动的谱分析法已得到其精确响应为[18]：

式中 ζ=γ（2ω n ）；Γ（⋅）为 Gamma 函数。考虑到响应为零均值高斯随机过程，在式（22）基礎上，可进一步推导得概率密度和其他统计量的精确解。根据概率论，可得如下与p （ H ）对应的特征函数 M（ z ）为：

其中 H 的各阶矩Eexact [ H n ]有如下精确解：

式中 2 F 1（⋅，⋅，⋅，⋅）为超几何函数。注意到fGn激励的线性系统响应仍然是高斯分布的，可以得到以下位移各阶矩的精确解：

前述宽带噪声激励下拟可积哈密顿系统随机平均法已经被应用于fGn激励下多自由度强非线性系统的响应预测和可靠性分析，并通过数值误差分析指出，当系统主频率落在fGn功率谱密度中比较平坦的范围内时，近似方法是适用的[16⁃17]。在这里，鉴于容易获得单自由度线性系统响应的解析解，仅对线性系统做出解析分析。考虑线性系统（21）受如下限带白噪声 W （ t ）激励（如图2中实线所示）：

系统均方响应为[2] ：

其中函数 I（ x ）如图3（ a ）所示。

由图3可见，阻尼率ζ越小，在ωω n =1处的 I （ x ）曲线越陡，这说明，只要区间（ω1，ω2）包括了ω n，就有 I（ω2ω n ）- I （ω1ω n ）≈1，限带白噪声的响应可以用白噪声的响应 E [ X 2]=πS0（2ζω n（3））来近似。再考虑 W （ t ）为 S（ω n ）= S0，（ω1，ω2）内的功率谱密度是具有斜率 S '（如图2中虚线所示）的限带噪声，即：

可以得到系统均方响应为（推导过程略）：

其中函数 J（ x，y ）如图3（b）所示。可见，斜率 S '改变了ωω n =1 处曲线的陡峭程度， J （ω2ω n，S 'ω n S0）- J （ω1ω n，S 'ω n S0）能否约等于1，也即 E [ X 2]能否近似为白噪声的响应，是受斜率 S '影响的。只有当斜率 S '比较小，即谱密度曲线比较平坦时才可以。

3 近似方法适用性的分析

在前述用宽带噪声激励下拟可积哈密顿系统随机平均法得到的fGn激励下单自由度非线性系统（1）响应的近似解析解p （ H ），E [ Hn ]和 E [ X 2n ]（见式（18），（19）和（20））中令 k =0，就得到fGn激励下线性系统（21）响应的近似解析解。同时，系统（21）的响应有精确解析解（见式（24）和（25））。这样就可以近似计算方法预测线性系统响应时的误差，比如：

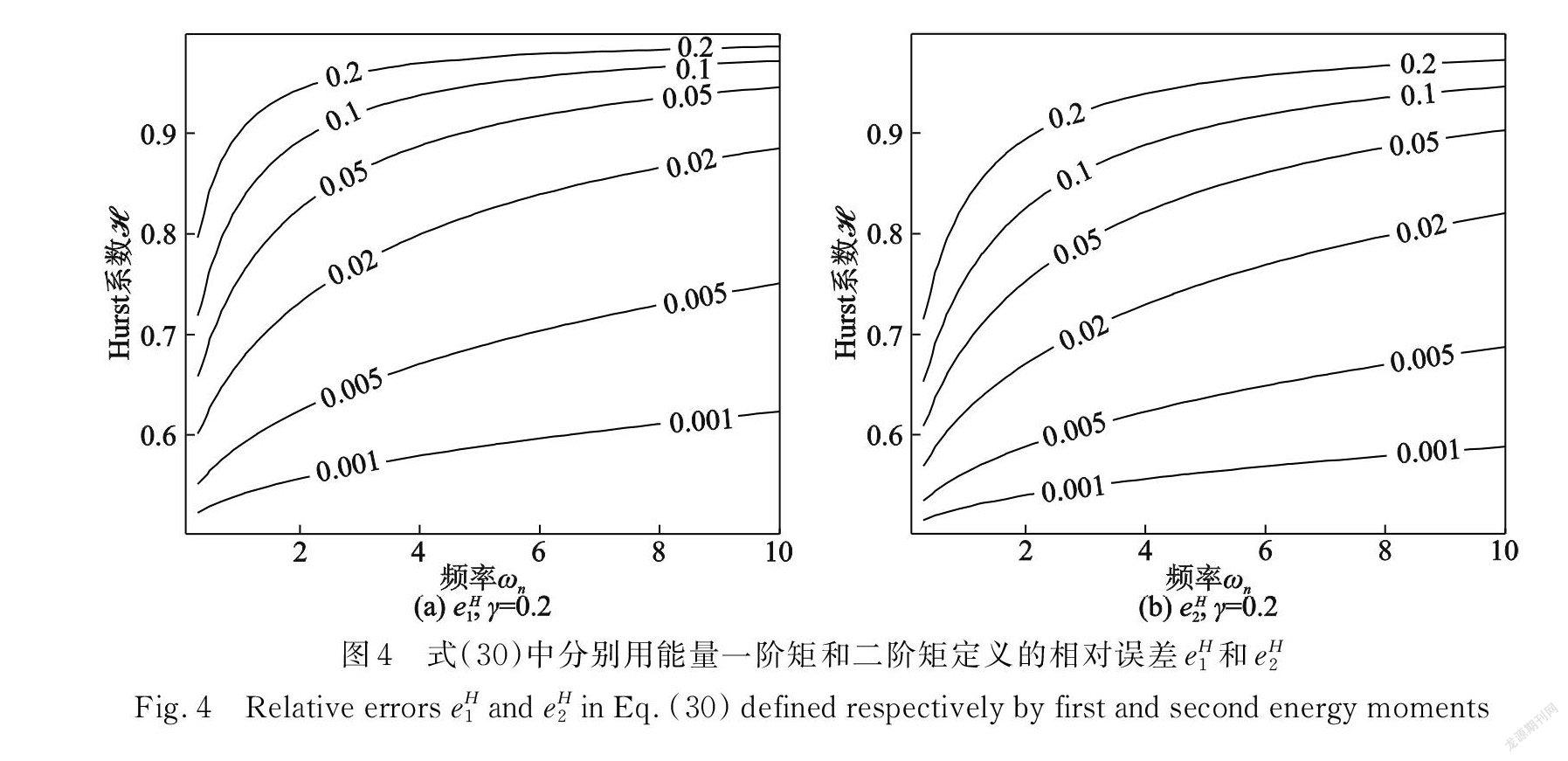
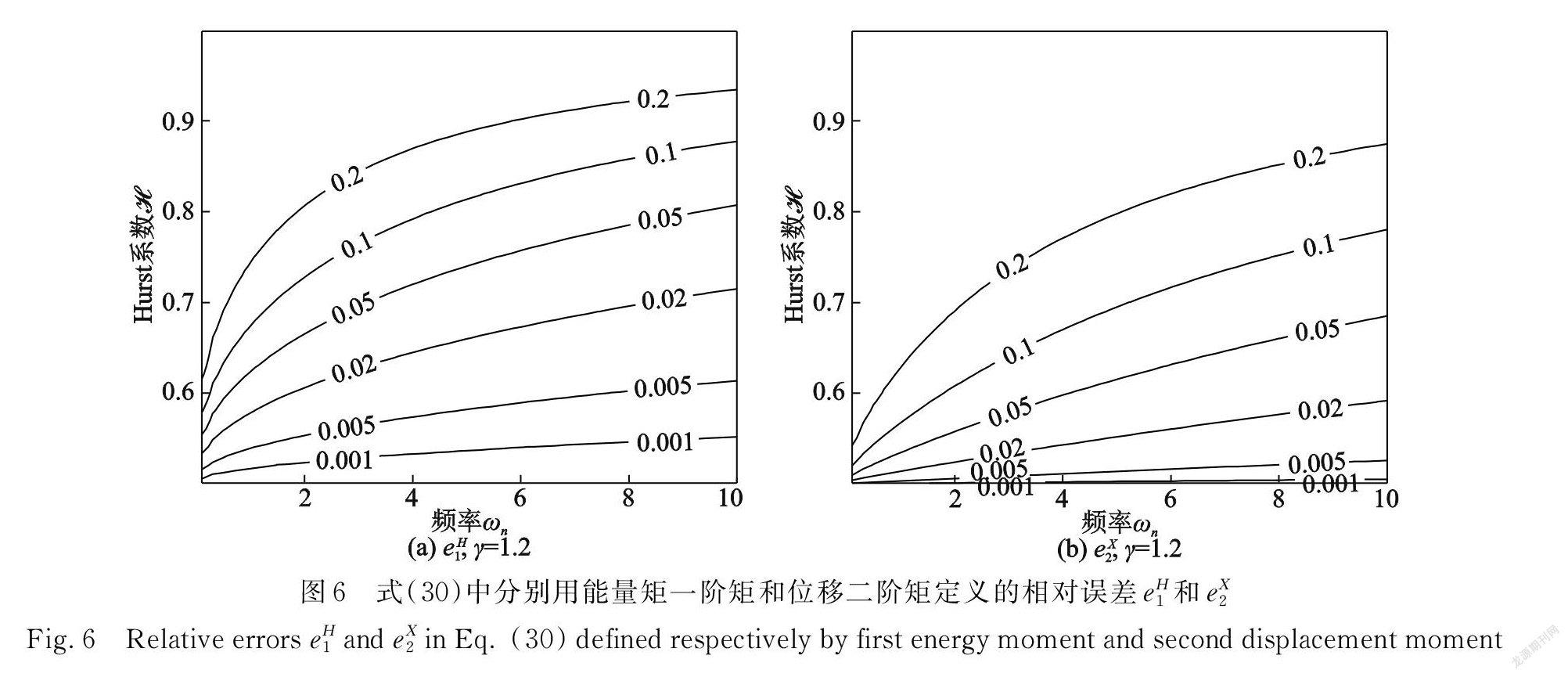
式中  e n（H）和 e2n（X）分别是用系统能量矩 E [ H n ]和位移矩 E [ X 2n ]来定义的相对误差。图 4，5显示了 e n（H）和 e2n（X）随 Hurst 系数ℋ、线性主频率ω n 及系统阻尼系数γ的变化情况。图 4，5表明，当ℋ越接近于和ω n 越大时，近似解的误差越小，原因在于此时fGn具有较宽的频带。图4，5还表明，对响应低阶矩 E [ H ]和E [ X 2]的近似解误差要低于对响应高阶矩 E [ H 2]和E [ X4]的近似解误差。γ=2ζω n 是线性系统（21）幅频响应特性的半功率带宽[2] ，它衡量了系统能在ω n 附近多大频率范围内吸收噪声的能量。比较图4（ a ）与图6（ a ），或比较图5（ a ）与图6（b）表明，γ增加时，近似解误差增加。观察近似解式（18），（19）和（20）可知，k =0时，fGn功率谱密度中仅谱值 S（ω n ）出现在近似解的表达式中，邻域噪声成分的影响被近似解忽略了，这就是γ增加，近似解误差增大的原因。

当fGn激励的非线性系统（1）中 k >0时，从近似解式（18），（19）和（20）可以看出，除退化线性系统频率ω n 外，其倍频3ω n，5ω n，…上的谱密度值和谱密度的各阶导数也出现在近似解的表达式中。因此，对于fGn激励的非线性系统（1），当退化线性系统频率及其倍频ω n，3ω n，5ω n，…都处于fGn功率谱密度曲线较为平坦的范围内时，误差较小，近似方法更适用。若要分析非线性因素对系统响应的影响，

可以借助式（18），（19）和（20）进行解析分析。由于哈密顿量 H 在非线性系统的响应预测、可靠性分析和稳定性分析中具有重要的地位，这里就以 H 为响应量进行分析。结合式（19）可知以下比值：

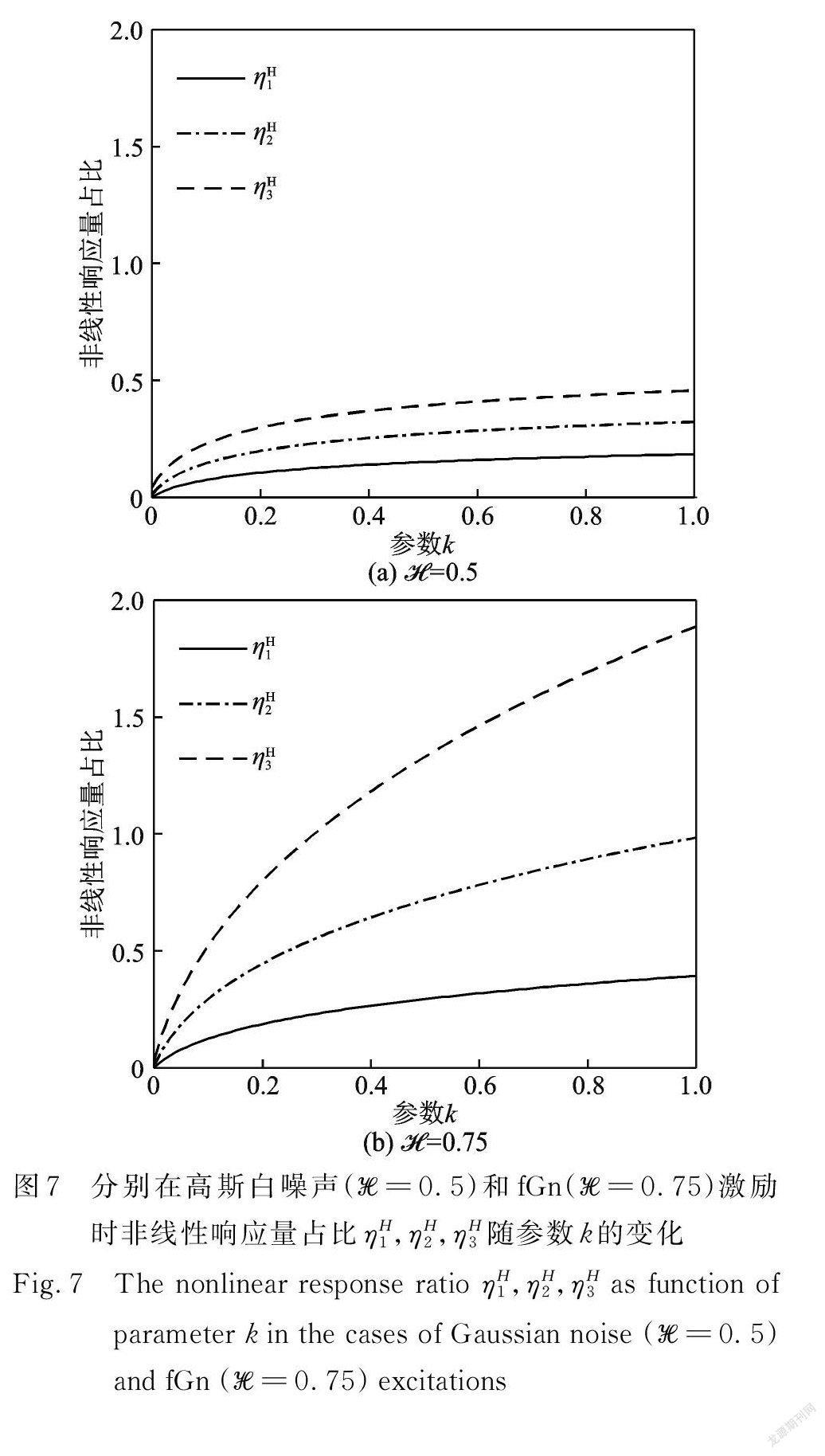
η n（H）表示在 n 阶能量矩 E [ H n ]中，由非线性因素k 带来的那部分响应量在整个响应量中的占比。图 7分别示出了高斯白噪声（ℋ=0.5）和fGn激励（ℋ=0.75）下非线性响应量占比随参数 k 的变化情况。图 7表明，无论高斯白噪声激励还是fGn激励，也无论 k 为何值，非线性因素对高阶矩的影响都要大于对低阶矩的影响。对图7（ a ）与图7（b）中相同η1（H），η2（H）或η3（H）的比较表明，高斯白噪声激励下η n（H）随 k 增加较缓慢，而fGn激励下η n（H）随 k 增加较急速。换言之，在 Hurst 系数ℋ和非线性因素 k 的共同影响下，能量矩 E [ H n ]有着非常大的变化。应用宽带噪声激励下拟可积哈密顿系统随机平均法所得到的理论结果能够准确地体现出非线性因素的影响。

4 结论

通过fGn激励下线性系统响应的精确解析解与用宽带噪声激励下拟可积哈密顿系统随机平均法所得的近似解析解之间的比较可知，只要系统固有频率所在频段的功率谱密度曲线比较平坦，近似解析解的误差就会较小。对于fGn激励的非线性系统，主频率及其倍数频率处的谱密度值和谱密度的各阶导数会影响解析解精度。可以预计的是，对强非线性系统，当fGn功率谱密度曲线在系统主频率及其倍数频率处较为平坦时，响应近似解析解的误差较小。分析表明，近似解析解也能反映出 Hurst 系数和非线性参数对响应量有较大的影响。总之，在fGn功率谱密度曲线较平坦的区域内，宽带噪声激励下拟可积哈密顿系统随机平均法适合于研究fGn激励下的多自由度强非线性系统的动力学。

参考文献：

[1] 朱位秋.随机振动[M].北京：科学出版社，1998.

Zhu  W  Q . Random  Vibration [M]. Beijing： Science Press，1998.

[2] 方同.工程随机振动[M].北京：国防工业出版社，1995.

Fang  T . Engineering  Random  Vibration[M]. Beijing： National Defense Industry Press，1995.

[3] 朱位秋.非线性随机动力学与控制— Hamilton 理论体系框架[M].北京：科学出版社，2003：238.

Zhu W Q . Nonlinear Stochastic Dynamics and Control— in Hamiltonian  Theory Formulation[M]. Beijing：Sci⁃ ence Press，2003：238.

[4]  Zhu W Q . Nonlinear stochastic dynamics and control inHamiltonian  formulation[ J ]. ASME  Applied  Mechan? ics Reviews，2006，59（4）：230⁃248.

[5]  Uchaikin V V . Fractional Derivatives for Physicists andEngineers ：Vol .I  Background  and  Theory [M]. Ber⁃ lin：Springer⁃Verlag，2012：144.

[6]  Uchaikin V V . Fractional Derivatives for Physicists andEngineers：Vol .  II   Applications  [M].   Berlin：Springer⁃Verlag，2012.

[7]  Mandelbrot B  B，Van Ness J W . Fractional Brownianmotions ，fractional  noises  and  applications [ J ]. SIAM Review，1968，10（4）：422⁃437.

[8]  Luo  A  C  J ，Afraimovich  V . Long⁃range  Interactions，Stochasticity  and  Fractional  Dynamics [M]. Beijing： Higher Education Press，2011.

[9]  Xu Y，Pei B，Guo R . Stochastic averaging for slow-fastdynamical systems with fractional Brownian motion[ J ]. Discrete  Continuous  Dynamical  Systems  Series  B，2015，20（7）：2257-2267.

[10] Xu  Y ，Pei  B ，Wu  J  L . Stochastic  averaging  principlefor differential equations with non-Lipschitz coefficients driven by fractional Brownian motion[ J ]. Stochastic and Dynamics，2017，17（2）：1750013.

[11] Pei B，Xu Y，Wu J L . Stochastic averaging for stochas⁃tic  differential  equations  driven  by  fractional  Brownian motion  and  standard  Brownian  motion [ J ]. Applied Mathematics Letters，2020，100：106006.

[12] Lü Q F，Deng M L，Zhu W Q . Stationary response ofmultidegree-of-freedom  strongly  nonlinear  systems  to fractional  Gaussian  noise [ J ]. Journal  of  Applied  Me⁃ chanics，2017，84（10）：101001.

[13] Deng M L，Lü Q F，Zhu W Q . Stochastic averaging ofquasi integrable and non-resonant Hamiltonian systems excited by fractional Gaussian noise with Hurst index H ∈（1/2，1）[ J ]. International Journal of Non-Linear Me⁃ chanics，2018，98：43-50.

[14] Biagini F，Hu Y，Øksendal B，et al. Stochastic Calcu ⁃lus  for  Fractional  Brownian  Motion  and  Applications [M]. London：Springer-Verlag，2008.

[15] Mishura Y S . Stochastic calculus for fractional Brown ⁃ian Motion and Related Processes[M]. Berlin：Spring⁃ er-Verlag，2008.

[16] Lü Q F，Zhu W Q，Deng M L . Response of quasi-inte⁃grable and non-resonant Hamiltonian systems to  frac⁃ tional Gaussian noise[ J ]. IEEE Access，2020，8（1）：72372-72380.

[17] Lü Q F，Zhu W Q，Deng M L . Reliability of quasi inte?grable  and  non-resonant  Hamiltonian  systems  under fractional Gaussian noise excitation[ J ]. Acta MechanicaSinica，2020，36（4）：902-909.

[18] Deng M L，Zhu W Q . Responses of linear and nonlin⁃ear oscillators to fractional Gaussian noise with Hurst in ⁃ dex between 1/2 and 1[ J ]. ASME Journal of Applied Mechanics，2015，82（10）：101008.

[19] Zhu W Q，Huang Z L，Suzuki Y . Response and stabili⁃ty of strongly non-linear oscillators under wide-band ran⁃ domexcitation[ J ]. International Journal of Non-Linear Mechanics，2001，36：1235-1250.

[20] Khasminskii R Z . On the averaging principle for Itôsto⁃chastic differential equations [ J ]. Kibernetka，1968，3（4）：260-279.

Analytical analysis on the applicability of an approximate method to nonlinear systems driven by fGn

DENG Mao-lin，ZHU Wei-qiu

（Institute of Applied Mechanics，School of Aeronautics and Astronautics，Zhejiang University，Hangzhou 310027，China）

Abstract： Due to the non-Markov property of response of a nonlinear system driven by fractional Gaussian noise （fGn），the diffu⁃ sion process theory cannot be applied . As an approximate method，the stochastic averaging method for multi-DOF strongly nonlin⁃ ear systems driven by wideband noise has been applied to study nonlinear systems driven by fGn . The results show that the approxi? mate method is very effective in the response prediction and the reliability analysis . However，so far there has been no analytical analysis on the error and applicability of the approximate method . In the present paper，the approximate method is applied to study a single-DOF nonlinear system driven by fGn and some analytical solutions are obtained . By comparing with reported exact analyti⁃ cal solutions，the error analysis is performed and the applicability of approximate method is determined . The conclusion of the pres⁃ ent paper can be the theoretical foundation for further application of the approximate method .

Key words： nonlinear system；wideband noise；fractional Gaussian noise （fGn）；stochastic averaging method of quasi Hamiltonian systems

作者简介：邓茂林（1973—），男，副教授。E-mail：mldeng@zju .edu .cn。

通讯作者：朱位秋（1938—），男，教授，中国科学院院士。电话：（0571）87991150；E-mail：wqzhu@zju .edu .cn。