基于变尺度Lempel⁃Ziv的滚动轴承损伤程度评估方法

崔玲丽 安加林 王鑫 张建宇

摘要：针对传统Lemple⁃Ziv复杂度（Lempel⁃Ziv complexity，LZC）计算过程中，二值化处理时会改变原序列的动力学特征以及计算效率较低的问题，结合轴承故障冲击特征，提出复合字典匹配追踪算法（compound dictionary matching pursuit algorithm，CDMP）与变尺度Lempel⁃Ziv复杂度（variable scale Lempel⁃Ziv complexity，VLZC）分析相结合的滚动轴承内外圈损伤程度评估方法。采用 CDMP 对原信号进行重构，检测信号周期性冲击成分；根据冲击幅值将重构信号分为轴承故障冲击区和冲击衰减区，对信号冲击进行变尺度二值化处理后，将冲击作为迭代基本元素，采用遍历查找法计算其 VLZC 指标；根据3σ原则给出内外圈不同损伤程度的 VLZC 取值区间，引入 BP 神经网络对其损伤程度进行智能分类。结果表明，该方法能有效降噪，保留信号周期性冲击特征，抑制非冲击成分，提高迭代计算效率，实现滚动轴承内外圈损伤程度的评估。

关键词：故障诊断；复合字典匹配追踪；变尺度Lempel⁃Ziv算法；二值化；BP 神经网络

中图分类号： TH165+.3；TH133.33    文献标志码： A    文章编号：1004-4523（2022）05-1250-09

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.023

引言

滚动轴承的运行状态直接影响整台机器的性能[1]。由于实际运行工况复杂、环境干扰等因素使得轴承容易出现损坏[2⁃3]。因此，滚动轴承故障检测与诊断具有重要意义[4]。目前，基于振动信号的轴承故障诊断研究主要集中在两个方面：轴承振动信号特征提取方法研究和轴承故障振动机理研究[5]。然而，这些方法大多针对轴承故障进行定性分析，对轴承故障损伤程度分析较少。随着现代设备发展，提取轴承故障特征并进行有效的故障程度诊断，实现故障状态监测尤为重要。

近年来，轴承故障损伤程度分析受到国内外学者的广泛关注。Jiang 等[6]将改进形态学滤波方法应用于轴承故障信号降噪和复杂度指标提取，得到了轴承信号复杂度与故障严重度之间的关系。Zhang 等[7]采用基于 EEMD 的排列熵指标对轴承故障类型和损伤程度进行分类。Cui 等[8]提出一种基于新字典模型的轴承故障诊断量化匹配追踪算法，初步实现滚动轴承故障的定量诊断。滚动轴承在运行过程中可以看作一个非线性动力学系统，通常用系统复杂度指标来描述。目前，许多学者应用Lempel⁃Ziv算法计算轴承故障信号的复杂性来进行轴承故障定量趋势诊断。

Lempel 和 Ziv[9]提出了复杂度算法，称为Lempel⁃Ziv复杂度。Hong 等[10]提出了一种基于连续小波变换的Lempel⁃Ziv复杂度轴承故障严重程度诊断方法，结果表明，对轴承所有转速，外圈故障尺寸越大，振動信号越复杂；内圈故障尺寸越大，振动信号周期性越强。窦东阳等[11]提出一种基于经验模态分解（EMD）和Lempel⁃Ziv指标的评价方法，得到了Lempel⁃Ziv值取值范围，对不同内外圈损伤进行了评价。张超等[12]提出一种基于 LMD 和Lempel⁃Ziv的方法，用于识别不同转速和不同内外圈缺陷严重程度的滚动轴承。文献[13⁃14]分别将Protrugram和Sparsogram与Lempel⁃Ziv相结合进行分析，验证了Lempel⁃Ziv复杂度指标在进行定量趋势诊断方面有一定的效果。前述方法聚焦于轴承故障特征提取方法研究，并将其与传统Lempel⁃Ziv复杂度算法相结合进行轴承故障诊断。但应用Lempel⁃Ziv复杂度算法处理轴承故障振动信号时，存在一定不足。第一，二值化过程会混淆故障冲击幅值，丢失部分故障信息；第二，迭代过程中并未考虑轴承故障冲击特征。因此，有必要探索一种更适合轴承故障振动信号处理的Lempel⁃Ziv复杂度算法。

为此，提出一种变尺度Lempel⁃Ziv复杂度滚动轴承损伤程度评估方法。首先，利用 CDMP 算法对信号进行重构；然后利用Protrugram处理重构信号得到最佳分析频带，将重构信号分为故障冲击区和冲击衰减区，并对其进行变尺度二值化处理。轴承发生故障时信号主要表现为冲击特征，因此将冲击作为迭代基本元素，迭代计算得到 VLZC 值，引入 BP 神经网络对其进行损伤程度智能分类。试验结果证明了基于变尺度Lempel⁃Ziv的滚动轴承损伤程度评估方法的有效性。

1 基本算法理论

1.1 滚动轴承故障模型

将轴承系统简化为一个单自由度线性时不变系统，轴承故障振动信号表示为：

式中 A（tn ）表示冲击响应信号的幅值；fn表示系统的共振频率；ξ表示相对阻尼系数；φ0表示冲击响应信号的初始相位角；tk表示第 k 个冲击响应的发生时刻；Δtk表示第 k 个和第 k⁃1个冲击响应之间的时间间隔。

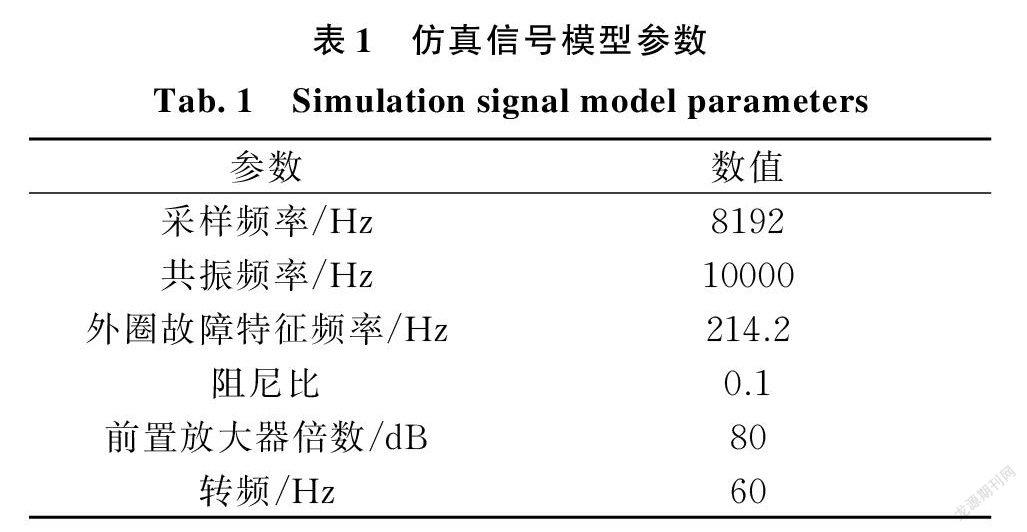
Lempel⁃Ziv复杂度算法本质是计算信号周期性，然而在实际故障轴承信号中，不可避免地会存在打滑、转速波动等现象，导致轴承振动信号冲击周期变化，对计算Lempel⁃Ziv值产生重要影响。该模型考虑滚动体在内、外圈滚道上会出现打滑现象，Δtk会出现随机波动，波动程度与轴承轴向和径向载荷比相关，取值一般为0.01～0.02[15]。仿真信号模型参数具体如表1所示。

考虑到轴承实际工作情况，引入高斯白噪声和有色噪声。仿真信号表达式为：

式中 x （tn ）为冲击信号；x1（t）为高斯白噪声；x2（t）为有色噪声；通过控制噪声的能量，使得仿真信号信噪比 SNR=−15 dB。

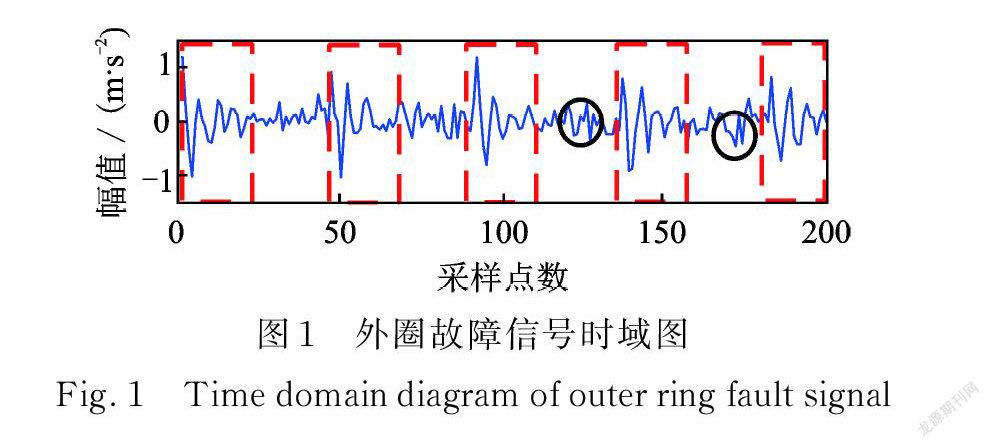
仿真信号如图1所示。可以看出，轴承单点故障以冲击特征为主，首先计算信号所有冲击幅值平均值，将其作为阈值划分标准，消除非故障冲击（圆圈标注处）后，将信号划分为故障冲击区（方框内）和冲击衰减区。信号中冲击分别为 Q1，Q2，Q3，…，Qm （ m≤n/3）。

将故障冲击区中的冲击分为正、负冲击，构成冲击成分 Qi 的采样点数为 j 个（任一采样点记为xio ），冲击幅值为 hi；冲击衰减区中冲击幅值较小，不考虑冲击方向，即三个连续采样点构成一个衰减冲击。

1.2 传统 Lempel-Ziv 算法

Lempel⁃Ziv复杂度基本过程是：将信号转换成二进制序列：如果 x （i）≥mean（x （ n ））（i=1，2，…， n ），则定义si =1（i=1，2，…，n ），否则si =0。定义 SN ={ s1，s2，…，sN }，定义信号复杂度为 Cn （ r），经过 n 次循环迭代得到最终的复杂度。

（1）当 r=0时，令Sv，0={ }，Q0={ }，Cn （0）=0。当 r=1时，令 Q1={Q0 s1}，由于 Q1不属于Sv，0，则 Cn （1）=Cn （0）+1=1，Q1={ }，r=r+1；

（2）令Qr ={Qr−1 sr }，Sv，r-1={Sv，r−2 sr−1}，判断Qr是否属于Sv，r−1。若是，则 Cn （ r）=Cn （ r-1），r=r+1；若否，则 Cn （ r）=Cn （ r-1）+1，Qr ={}，r=r+1；重复步骤（2）。

上述 Cn （ r）值受 SN 的长度 n 影响明显，为了得到相对独立的指标，Lempel 和 Ziv 提出归一化公式：

最后，通过归一化计算出 Lempel⁃Ziv 复杂度。

1.3 变尺度 Lempel-Ziv 算法

传统 Lempel⁃Ziv 复杂度算法中存在两点局限性：

（1）在二值化部分，将信号点平均值作为二值化阈值，对信号进行二值化会混淆冲击幅值大小，造成轴承故障特征畸变，如图2（ a ）所示，通过图1和图2（ a ）可以看出，信号（图1）经过二值化后衰减冲击幅值被放大，故障信息不能有效保留，不能保证计算结果的有效性。

（2）在迭代计算部分，并未考虑轴承故障的冲击特征，而是仅应用其数学思想，将信号点作为Lempel⁃Ziv复杂度算法迭代的基本元素，当有新元素（采样点）加入时就进行一次迭代计算，耗时长，效率低，信号点数为 n，迭代计算次数为（ n −1）次。

综上所述，针对传统Lempel⁃Ziv两点局限性，提出变尺度Lempel⁃Ziv算法，分别在故障冲击区和冲击衰减区计算冲击幅值（hi ）及时间尺度（ Ti =（j−1）/fs ），并对其作变尺度二值化处理，变尺度二值化步骤如下：

（1）对信号中冲击幅值 hi 求均值得到 mean（hi ），将 mean（hi ）作为二值化划分标准。正冲击记为1，负冲击或衰减冲击记为0（括号内表示正负冲击或衰减冲击）。

（2）若为正冲击，当 hi≥mean（hi ）时，令xio =（1）1；当 hi≤mean（hi ）时，令xio =（1）0；若为负冲击，当 hi≥mean（hi ）时，令xio =（0）1；当 hi≤mean（hi ）时，令xio =（0）0；若为衰减冲击，则令xio =（0）0。

通过图1和图2（b）可以看出，该方法能突出轴承故障特征，抑制非冲击成分。

如图3所示，滚动轴承故障特征主要表现为冲击特征，因此将冲击作为迭代基本元素，迭代计算时，每加入一个冲击元素（Qv，r ），采用遍历查找法与已有冲击序列进行比对，依次迭代。如下式所示：

构成冲击采样点数最少为3个信号点，改进后迭代次数最多为（ n/3）−1次，大大提高了计算效率。迭代计算步骤如下：

（1）当 r=0时，定义 Qv ，0={ }， Q0={ }， Cn （0）=0。

（2）当 r=1时，由于 Q1不属于 Qv，0，则 r=r+1， Cn （1）=Cn （0）+1=1；

（3）令 Qv，r ={Qv，r-1，Qr }，判斷 Qr+1是否属于 Qv，r 。若属于，则 Cn （ r+1）=Cn （ r），r=r+1，Qv，r+1={Qv，r }。若不属于，则 r=r+1，Cn （ r+1）=Cn （ r）+1，Qv，r+1={Qv，r，Qr+1}；重复步骤（3），直至迭代完成。

1.4 MP 算法原子库

给定一个集合 D={gk，k=1，2，…，K }，其元素是在整个 Hilbert 空间 H=RN 的单位矢量，集合 D 称为原子库，其元素称为原子。由于原子库的冗余性（ K≫N），矢量gk是线性的。对于任意长度为 N 的实信号f∈H，在 D 中找到由 m 个原子组成的线性组合：

上式即信号的稀疏分解，其中 ck 为分解系数。

以正弦函数作为傅里叶字典的基元函数：

式中 f为频率参数；λ为相位参数；Kfou为归一化系数。

保证每个原子具有单位能量，即ϕ fou （ f，λ） =1；

以指数函数与正弦函数乘积得到的指数衰减函数作为冲击时频字典的基元函数[16]：

式中 p 为冲击响应的阻尼衰减特性；u 为冲击响应事件发生的初始时刻（ s ）；f为系统的阻尼固有频率（ Hz ）；ϕ为相位参数；Kimp为归一化系数。

2 基于变尺度 Lempel-Ziv 的滚动轴承损伤程度评估方法

针对传统Lempel⁃Ziv复杂度计算过程中改变信号动力学特征以及计算效率低的问题，本文提出一种基于变尺度Lempel⁃Ziv的滚动轴承损伤程度评估方法。首先，利用 CDMP 对原始信号进行重构；然后利用Protrugram分析得到最佳分析频带，并计算最优分析频带的 VLZC 值，最后进行复杂度值区间划分以及轴承损伤程度分类。

假设振动信号为 x （t），CDMP⁃VLZC 算法步骤如下：

（1）针对轴承故障信号特点，选择字典为傅里叶字典（式（8））和冲击时频字典（式（9））构成的复合字典，确定迭代终止条件，对原始信号 x （t）进行 CD ⁃ MP 处理。

（2）利用Protrugram处理重构信号得到最优分析频带：

①对重构信号进行傅里叶变换，并确定中心频率、带宽、步长等参数。

②计算窄带包络谱和其峭度，选取峭度最大的频带作为最佳分析频带。

（3）对最佳频带进行区间划分，得到故障冲击区和冲击衰减区；并对各个冲击进行变尺度二值化处理。

（4）将冲击作为迭代基本元素，计算得到 VLZC 值，并根据3σ原则划分内外圈不同损伤程度的 VL ⁃ ZC 指标取值区间。

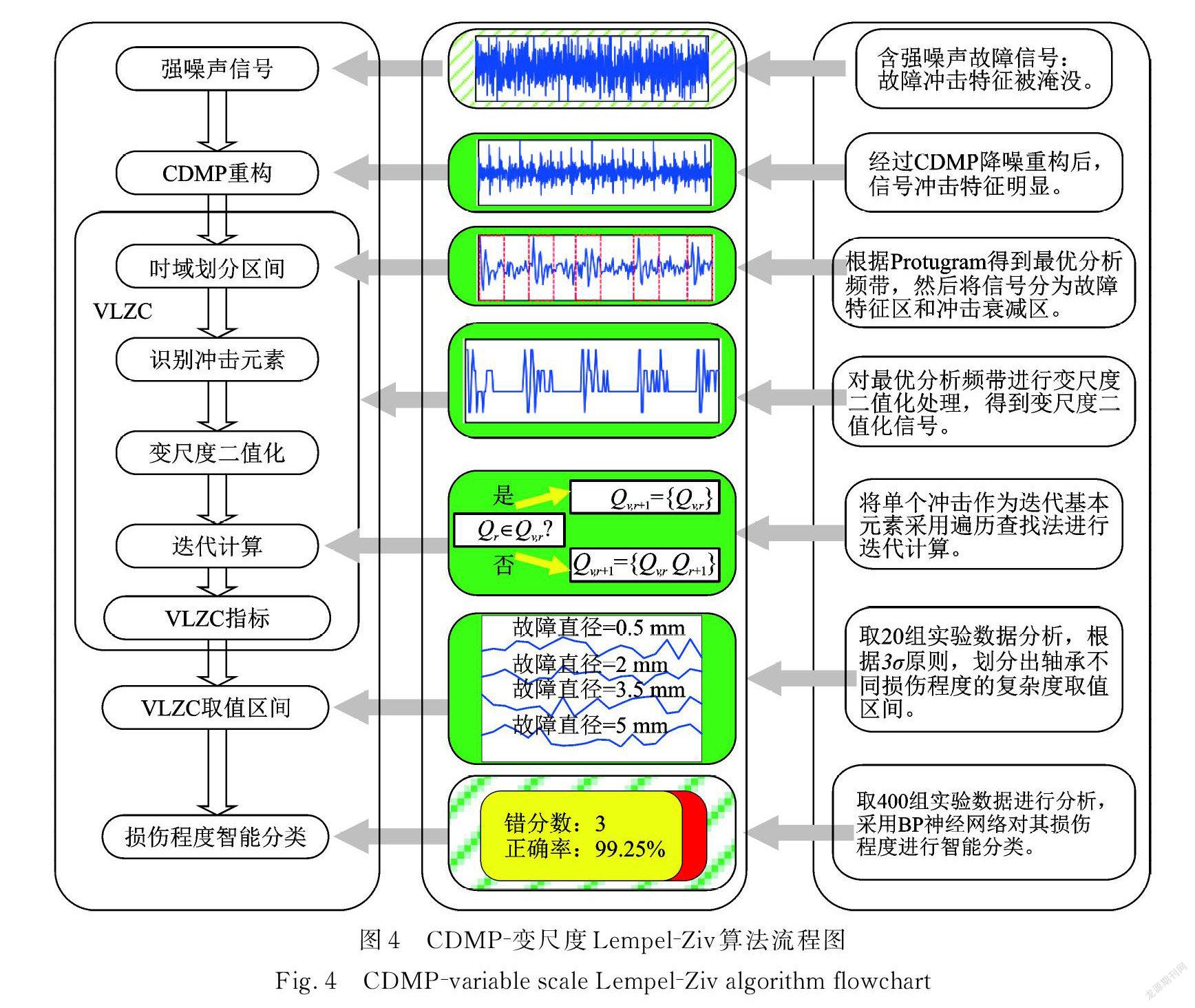
（5）引入 BP 神经网络对其进行损伤程度智能分类。具体算法流程如图4所示。

3实验验证

对不同损伤程度的滚动轴承内外圈故障的实验数据进行故障特征提取，划分其内外圈不同损伤程度的 CDMP⁃VLZC 取值区间，并采用 BP 神经网络对滚动轴承内外圈不同损伤程度进行智能分类。

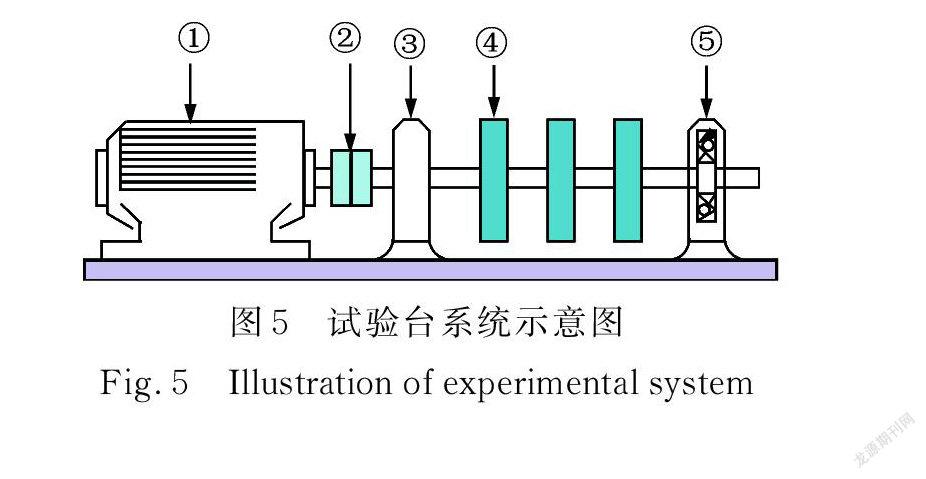
为了验证本文提出方法有效性，采用滚动轴承内、外圈故障信号进行验证分析。实验系统由轴承实验台、HG3528A 数据采集仪、笔记本电脑组成。其中轴承实验台（图5）由三相异步电机①通过挠性联轴器②与装有转子④的转轴连接，轴由两个6307轴承支撑，③为正常轴承，⑤为不同故障大小的轴承。电机转速R=1497 r/min，轴承的大径D=80mm，小径 d=35 mm，滚动体个数为 Z=8，接触角α=0°，加速度传感器固定在轴承座的正上方和水平方向，采样频率为16384 Hz，采样点数为8192个。在轴承的内、外圈滚道中央加工出直径大小分别为0.5，2，3.5和5 mm 的凹坑模拟点蚀故障，得到不同故障尺寸的内、外圈轴承故障实验信号，用来模拟滚动轴承的不同程度损伤。

3.1  外圈故障试验

外圈故障轴承实验信号如图6（ a ）所示，采用 CDMP ⁃VLZC 方法对外圈故障轴承信号进行分析，结果如下。

首先对原始信号进行 CDMP 重构处理，重构信号如图6（b）所示，可以看出冲击特征明显。重构信号频谱图如图7所示，并且可以找到外圈故障特征频率及其倍频。如78.7 Hz（外圈故障特征频率fo ）、157.5 Hz（二倍外圈故障特征频率2fo ），CDMP 方法能够对轴承外圈故障信号有效降噪。

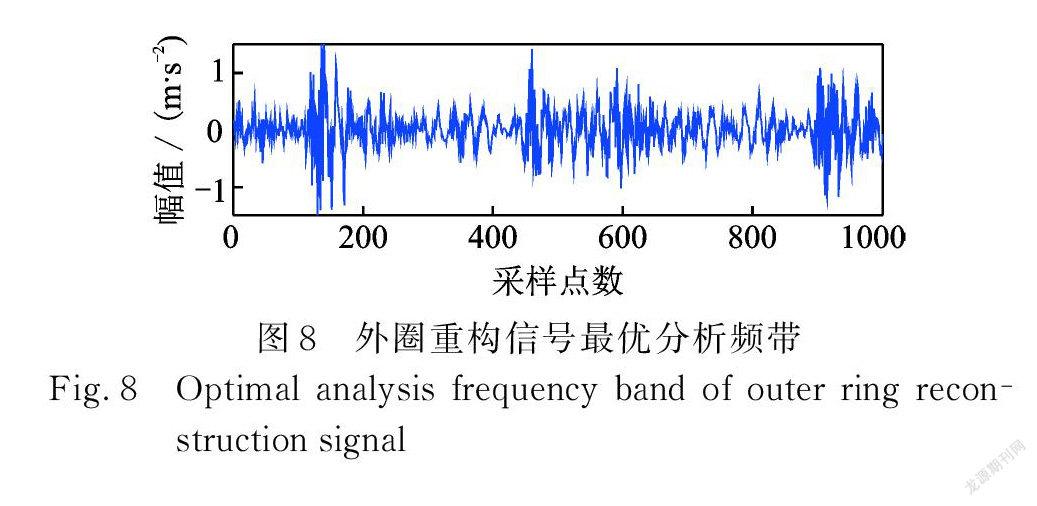
由外圈故障频率为78.73 Hz，确定带宽 BW 为300 Hz，步长 Step 为100 Hz，中心频率取值范围为[150 Hz，3000 Hz ]，利用Protrugram得到最优分析频带，如图8所示。然后对冲击进行变尺度二值化处理，变尺度二值化信号如图9所示，保留了部分轴承故障冲击特征，抑制非冲击特征。

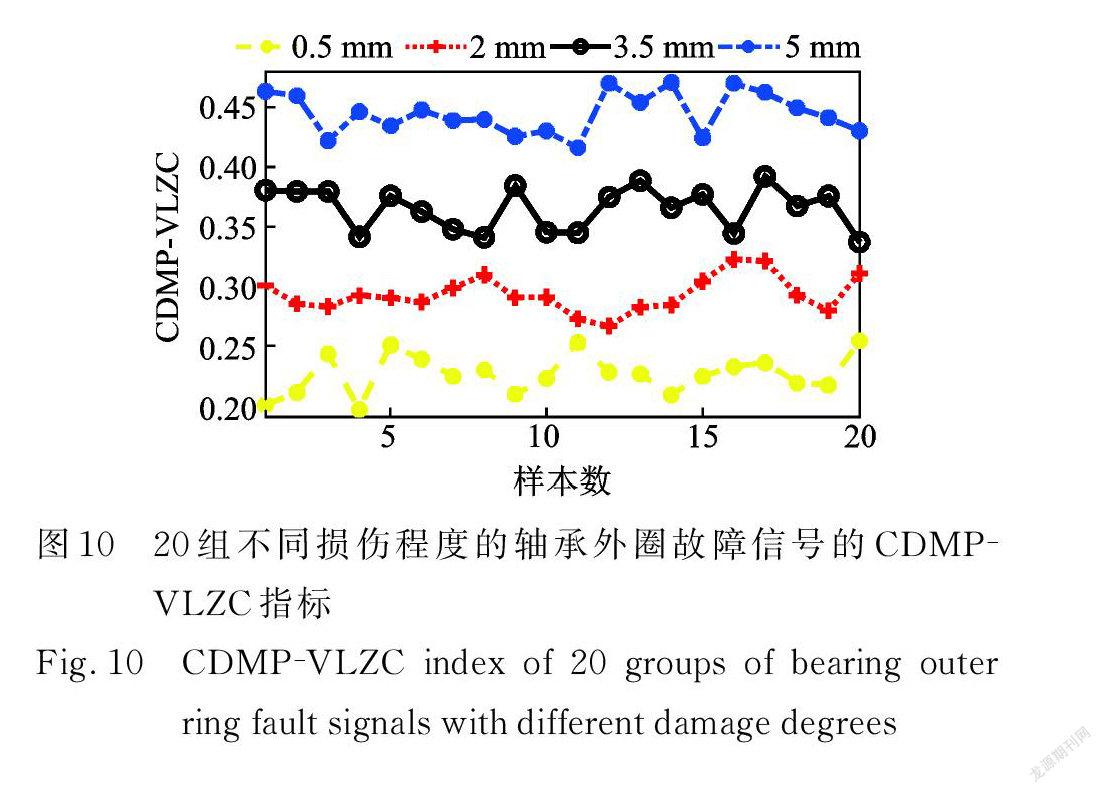
分别选取20组故障直径大小为0.5，2，3.5，5 mm 的外圈故障数据样本。样本长度为4096，计算各损伤程度的轴承外圈故障信号的 CDMP⁃VLZC 指标，其计算结果如表2和图10所示。

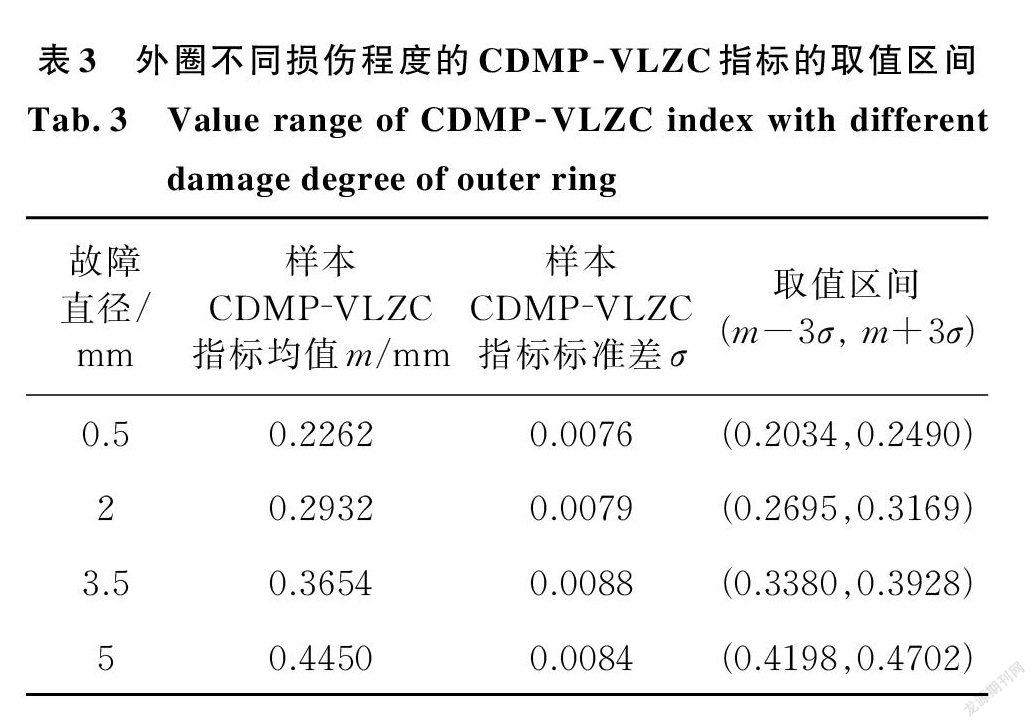
从图10可以看出，CDMP ⁃VLZC 指标可以区分出滚动轴承外圈故障信号的不同损伤程度，并且随着故障尺寸的增大，轴承外圈的 CDMP⁃VLZC 指标呈现上升趋势。根据统计学的“3σ”原则，划分出外圈不同损伤程度的 CDMP⁃VLZC 指标的取值区间，见表3。

BP 神经网络具有较强的非线性映射能力和自学习能力，将 CDMP⁃VLZC 作为轴承损伤程度智能分类的输入分量输入到 BP 神经网络分类系统中，以轴承外圈损伤状态为输出，实现轴承损伤程度智能诊断。

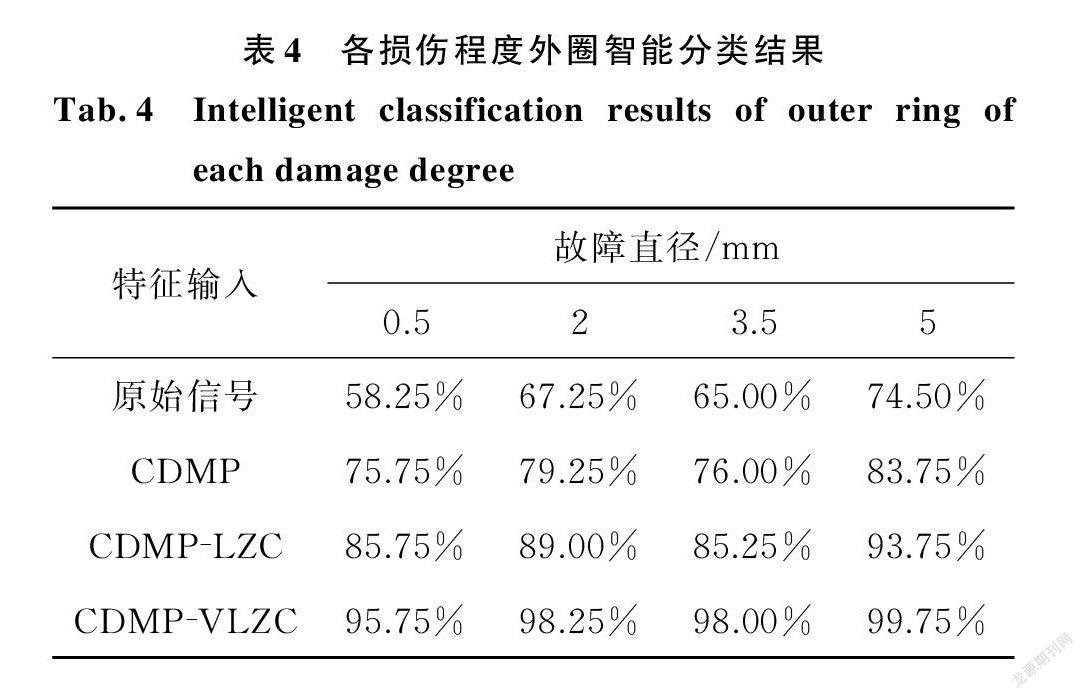
根据轴承外圈的损伤程度实验数据，采用其中20组特征矢量及其标签作为训练样本集，400组作为测试样本集。 BP 神经网络所选的特征参数为 CDMP ⁃VLZC，所以选用输入层节点数为1。输出层节点是直接判断轴承损伤程度的依据，将轴承损伤程度类型采用二进制编码方式。直径0.5 mm 损伤编码为（0，0），直径2 mm 损伤编码为（0，1），直径3.5 mm 损伤编码为（1，0），直径5 mm 损伤编码为（1，1），所以输出节点为4。考虑到计算效率问题，选取网络的隐层数为1层。根据训练效果，隐层节点设为11，并且隐层神经元的激活函数和输出层神经元激活函数选用 S 型。智能分类结果如表4所示。

对于故障直径为0.5，2，3.5，5 mm 的轴承外圈故障信号，将其原始信号、CDMP 重构信号、 CDMP ⁃LZC 指标、CDMP ⁃VLZC 指标作为输入分别输入到 BP 神经网络，智能分类结果如表4所示。可以看出，对于不同故障尺寸的轴承信号， CDMP ⁃VLZC 作为特征输入的 BP 神经网络分类系统效果明显优于原始信号、CDMP 重构信号、 CDMP ⁃LZC 指标作为特征输入的分类效果。

3.2  内圈故障试验

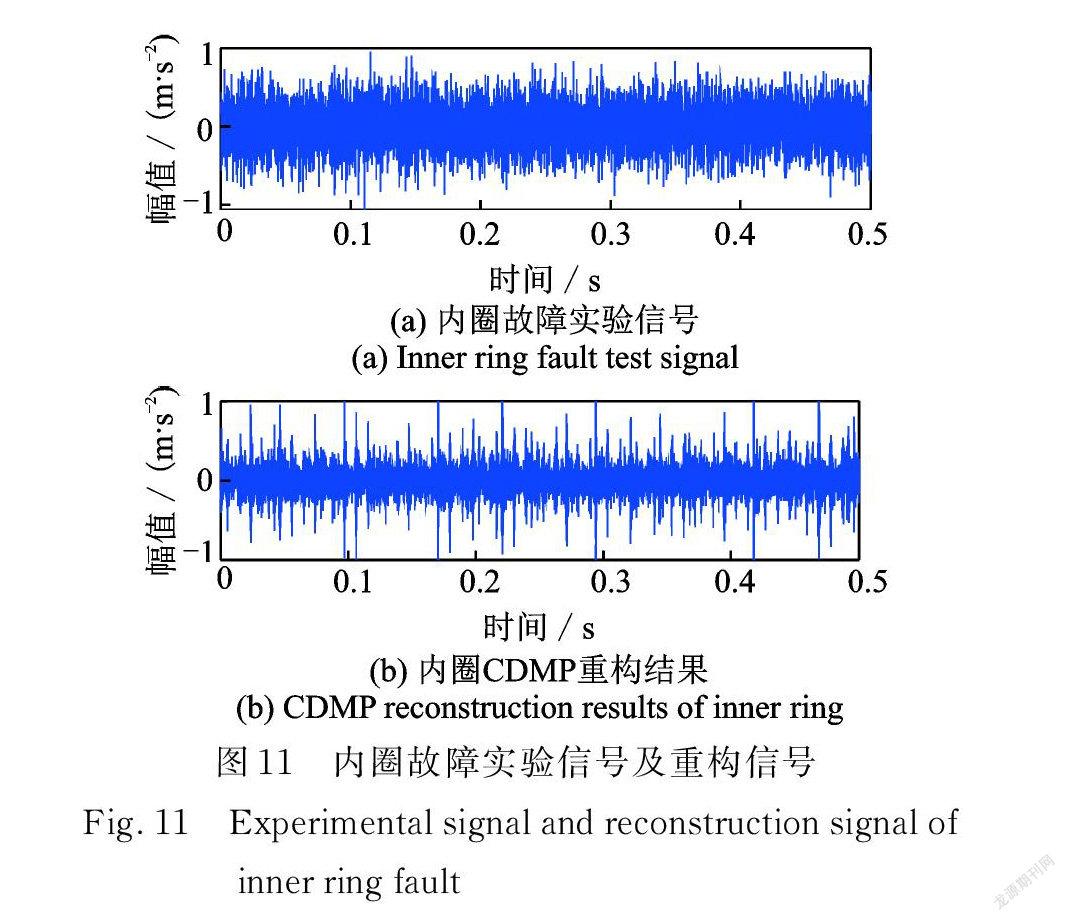
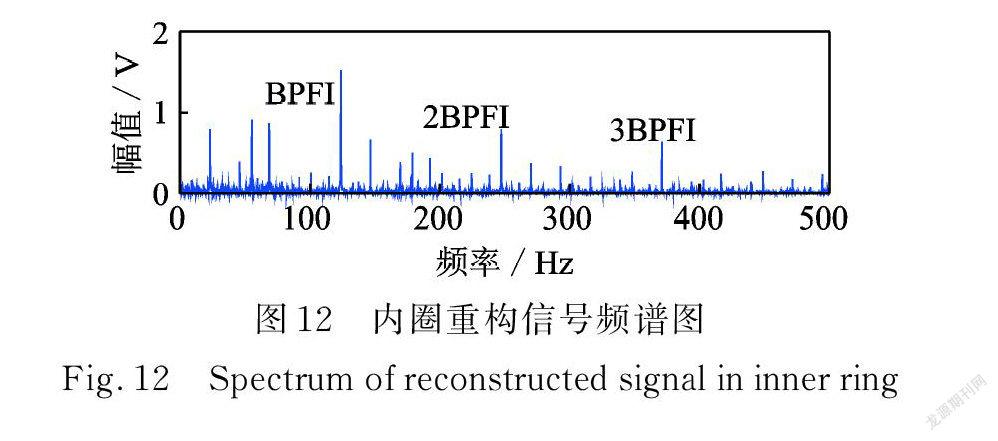
内圈故障轴承实验信号如图11（ a ）所示，采用 CDMP ⁃VLZC 方法对内圈故障轴承信号分析，结果如下。首先对内圈故障信号 x （t）进行 CDMP 重构处理，重构信号如图11（b）所示，冲击特征较明显。重构信号频谱如图12所示，可以找到内圈故障特征频率（BPFI ）及其倍频。如123.74 Hz（内圈故障特征频率fi ）、247.4 Hz（二倍内圈故障特征频率2fi ），CD⁃ MP 方法能够对轴承内圈故障信号有效降噪。

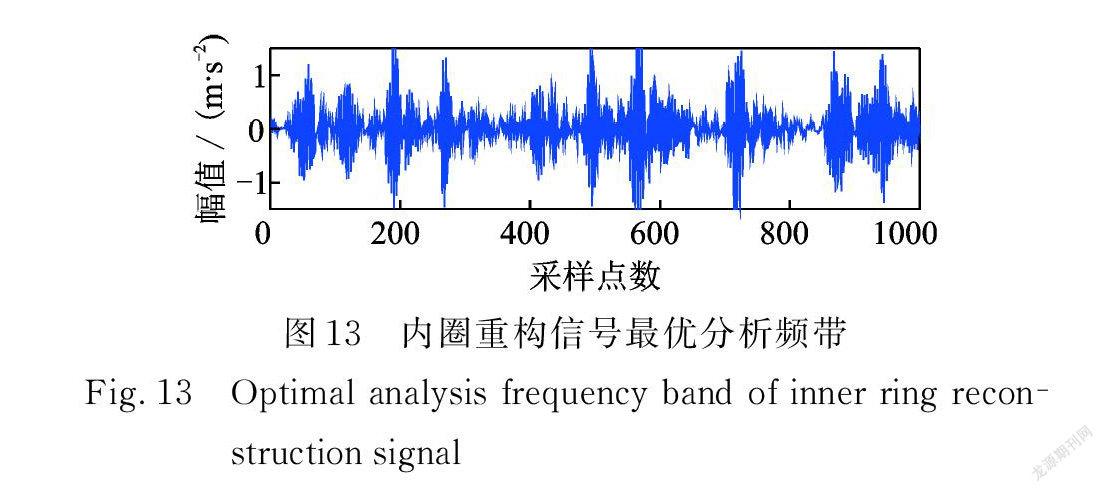
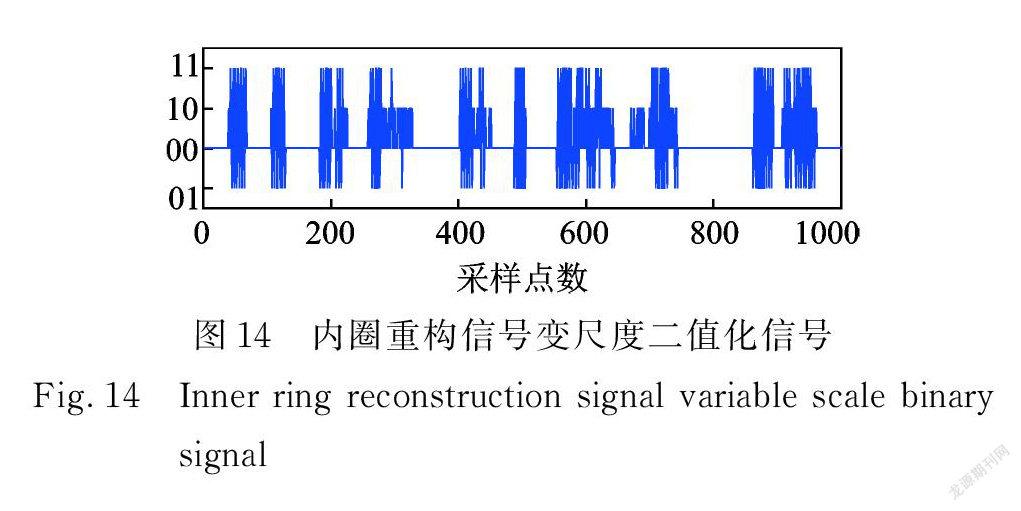
由内圈故障頻率为123.738 Hz，确定带宽 BW 为400 Hz，步长 Step 为100 Hz，中心频率取值范围为[200 Hz，3000 Hz ]，利用Protrugram得到最优分析频带，如图13所示；然后对冲击进行变尺度二值化处理，变尺度二值化信号如图14所示，保留了部分轴承故障冲击特征，抑制非冲击特征。

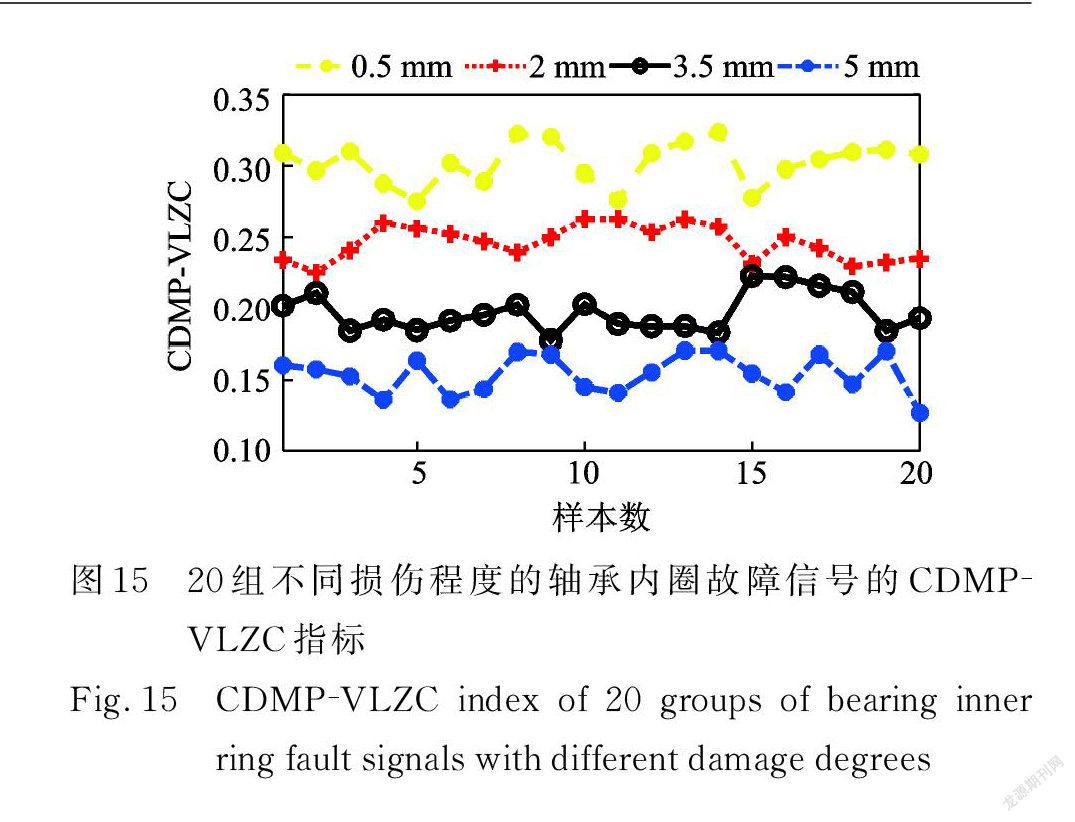
同样选取20组故障直径大小为0.5，2，3.5，5 mm 的内圈故障数据样本，样本长度为4096，计算各损伤程度的轴承内圈故障信号的 CDMP ⁃VLZC 指标，计算结果如表5和图15所示。

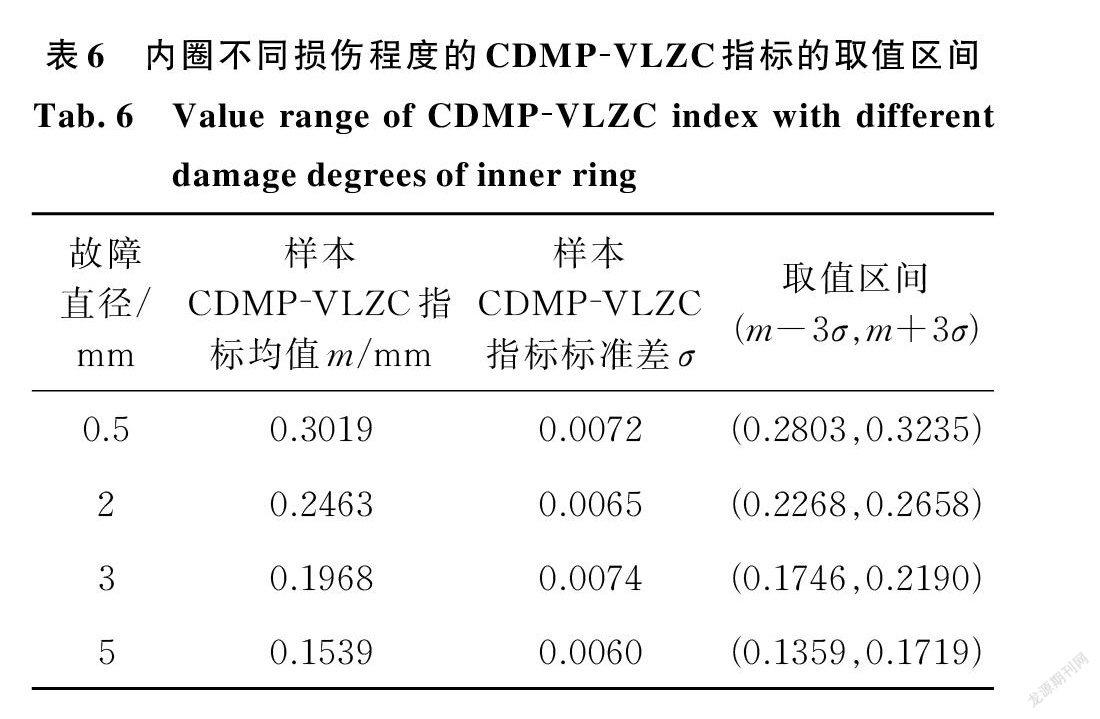
从图15可以看出，CDMP ⁃VLZC 指标可以区分出滚动轴承内圈故障实验信号的不同损伤程度，并且随着故障尺寸增大，轴承内圈故障信号的 CDMP ⁃VLZC 指标呈现下降趋势。根据统计学的“3σ”原则，划分出内圈不同损伤程度的 CDMP ⁃VLZC 指标的取值区间如表6所示。

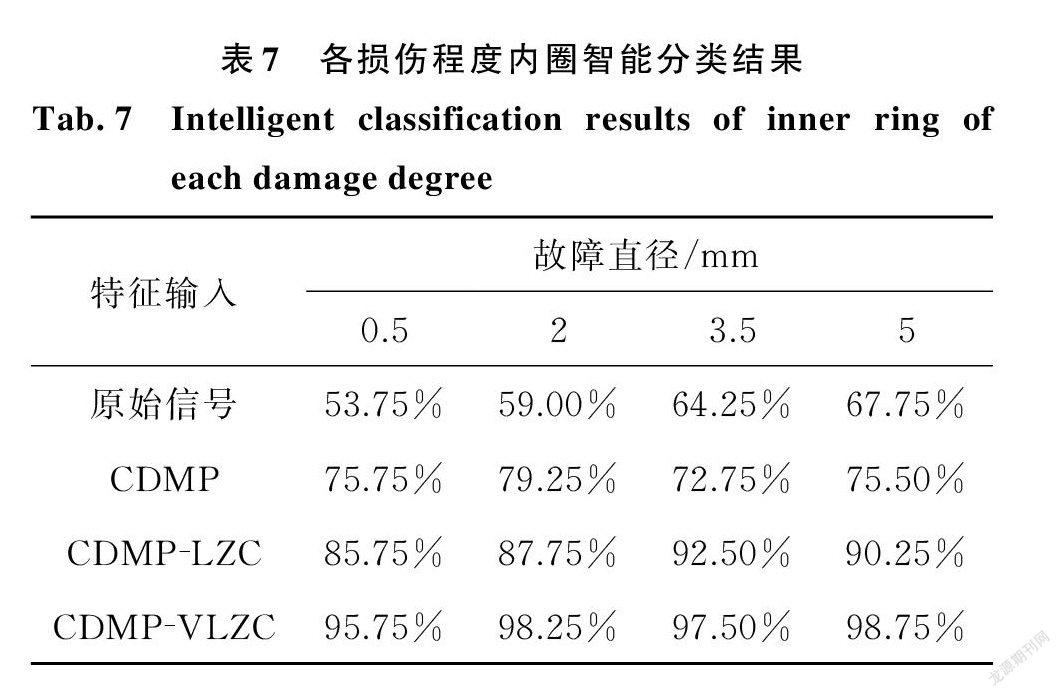
同样，将 CDMP⁃VLZC 作为轴承损伤程度智能分类的输入分量输入到 BP 神经网络分类系统中，以轴承外圈损伤状态为输出，实现轴承损伤程度智能诊断。采用其中20组特征矢量及其标签作为训练样本集，400组作为测试样本集。智能分类结果如表7所示。

对于故障直径为0.5，2，3.5，5 mm 的轴承内圈故障信号，将其原始信号、CDMP 重构信号、 CDMP ⁃LZC 指标、CDMP ⁃VLZC 指标作为输入分别输入到 BP 神经网络，智能分类结果如表7所示。可以看出，对于不同故障尺寸的轴承信号，CDMP ⁃ VLZC 作为特征输入的 BP 神经网络分类系统效果明显优于原始信号、CDMP 重构信号、CDMP ⁃LZC 指标作为特征输入的分类效果。

综上所述，采用 CDMP 方法对信号降噪效果明显，并且结合 VLZC 指标和 BP 神经网络可以实现滚动轴承损伤程度智能分类。

4 结论

针对传统Lempel⁃Ziv二值化会改变原序列的动力学特征以及计算效率较低的问题，本文提出一种 CDMP 与 VLZC 分析相结合的滚动轴承内外圈损伤程度评估方法。

（1）首先，采用 CDMP 对原始信号降噪重构。再利用Protrugram处理重构信号得到最佳分析频带，然后对其进行变尺度二值化处理，将冲击作为迭代基本元素计算得到 VLZC 指标。将 CDMP ⁃VLZC 指标输入 BP 神经网络分类系统中，实现滚动轴承损伤程度智能诊断。实验处理结果表明，应用 CDMP⁃VLZC 方法能够有效对滚动轴承损伤程度进行智能分类。

（2）变尺度Lempel⁃Ziv算法在将信号划分为故障冲击区和冲击衰减区时，采用自适应阈值进行划分，由于内圈信号幅值存在周期性变化，对于内圈轴承故障信号智能分类时效果相对较差，如何更精确地区分故障冲击区和冲击衰减区，可作为下一步工作重点。

参考文献：

[1] 梅宏斌.滚动轴承振动监测与诊断：理论·方法·系统[M].北京：机械工业出版社，1996.

MEI Hongbin . Vibration Monitoring and Diagnosis of    Rolling  Bearing [M]. Beijing：China  Machine  Press，1996.

[2]  Claasen  T  A  C  M ，Mecklenbrauker  W . The  Wignerdistribution  a tool  for time  frequency  analysis，Part 1： continuous time signals[ J ]. Philips Journal of Research，1980，35（4）：217-250.

[3] 张中民，卢文祥，杨叔子，等．基于小波系数包络谱的滚动轴承故障诊断[ J ]．振动工程学报，1998，11（1）：65-69．

Zhang  Zhongmin， Lu  Wenxing， Yang  Shuzi， et  al . Fault diagnosis of rolling bearing based on wavelet coef⁃ ficient envelope spectrum [ J ]. Journal of Vibration En ⁃ gineering，1998，11（1）：65-69.

[4]  Huang N  E，Shen Z，Long  S R，et al．The  empiricalmode decomposition  and the Hilbert spectrum  for non⁃ linear  and  non-stationary  time  series  analysis [ J ]. Pro ⁃ ceedings Mathematical Physical & Engineering  Scienc⁃ es，1998，454（1971）：903-995．

[5] 缪荣松．基于小波-包络的重载货运列车滚动轴承振动故障诊断[ D ]．长沙：中南大学，2011．

Miao  Rongsong . Vibration  fault  diagnosis  of  rolling bearing of heavy haul freight train based on wavelet en⁃ velope [ D ]. Changsha：Central South University，2011.

[6]  Jiang K，Xu G，Liang L，et al . A quantitative diagnosismethod for rolling element bearing using signal complex? ity  and  morphology  filtering[ J ]. Journal  of Vibroengi⁃ neering，2012，14（4）：1862-1875.

[7]  Zhang X，Liang Y，Zhou J，et al . A novel bearing faultdiagnosis model integrated permutation entropy，ensem ⁃ ble  empirical mode decomposition  and  optimized  SVM [ J ]. Measurement，2015，69：164-179.

[8]  Cui L，Wu N，Ma C，et al . Quantitative fault analysisof  roller  bearings  based  on  a  novel  matching  pursuit method with a new step-impulse dictionary[ J ]. Mechan ⁃ ical Systems & Signal Processing，2016，68-69：34-43.

[9]  Lempel A，Ziv J． On the complexity of finite sequences[ J ]． IEEE Transaction on Information Theory，1976，22（1）：75-81．

[10] Hong H，Liang M．  Fault severity assessment for roll⁃ing  element  bearings  using  the  Lempel-Ziv  complexity and continuous wavelet transform[ J ]． Journal of Sound and Vibration，2009，320：452-468．

[11]窦东阳，赵英凯．基于 EMD 和 Lempel-Ziv 指标的滚动轴承损伤程度识别研究[ J ]．振动与冲击，2010，29（3）：5-8．

Dou Dongyang，Zhao Yingkai . Research on damage de⁃ gree identification of rolling bearing based on EMD and Lempel Ziv index [ J ]. Journal of Vibration and Shock，2010，29（3）：5-8.

[12]张超，陈建军．基于 LMD 和 Lempel-Ziv 指标的滚动轴承故障损伤程度研究[ J ]．振动与冲击，2012，31（16）：77-82．

Zhang Chao，Chen Jianjun . Study on damage degree of rolling bearing fault based on LMD and Lempel Ziv in⁃ dex[ J ]. Journal of Vibration and Shock，2012，31（16）：77-82.

[13] Du Jianxi，Cui Lingli，Zhang Jianyu，et al . The methodof  quantitative  trend  diagnosis  of  rolling  bearing  fault based on Protrugram and Lempel-Ziv[ J ]. Shock and Vi? bration，2018：4303109.

[14] Cui Lingli，Li Beibei，Ma Jianfeng，et al . Quantitativetrend fault diagnosis of a rolling bearing based on Spar⁃ sogram and Lempel-Ziv[ J ]. Measurement，2018，128：410-418.

[15]赵德尊，王天杨，褚福磊.基于自适应广义解调变换的滚动轴承时变非平稳故障特征提取[ J ].机械工程学报，2020，56（3）：80-87.

Zhao  Dezun， Wang  Tianyang， Chu  Fulei . Adaptive generalized   demodulation   based   rouingbearingtime⁃varing  nonstationary  fault  feature  extraction [ J ]. Journal of Mechanical Engineering，2020，56（3）：80-87.

[16]崔玲丽，王婧，邬娜，等.基于轴承故障信号特征的自适应冲击字典匹配追踪方法及应用[ J ].振动与冲击，2014，33（11）：54-60.

Cui Lingli，Wang Jing，Wu Na，et al . Bearing fault diag⁃ nosis based on self⁃adaptive impulse dictionary matching pursuit [ J ]. Journal  of  Vibration  and  Shock，2014，33（11）：54⁃60.

Evaluation method of rolling bearing damage degree based on variable scale Lempel-Ziv

CUI Ling-li，AN Jia-lin，WANG Xin，ZHANG Jian-yu

（Beijing Key Laboratory of Advanced Manufacturing Technology，Faculty of Materials and Manufacturing，Beijing University of Technology，Beijing 100124，China）

Abstract： In the traditional Lempel-Ziv complexity （LZC） calculation process，the binary processing changes the dynamic charac? teristics of the original sequence and lead to the low computational efficiency . Combined with the impact characteristics of bearing faults，a compound dictionary matching pursuit （CDMP） algorithm is proposed，and variable scale Lempel-Ziv complexity （VL⁃ ZC） analysis is combined to evaluate the damage degree of inner and outer rings of rolling bearings . CDMP is used to reconstruct the original signal and detect the periodic impact component in the signal . According to the impact amplitude，the reconstructed sig⁃ nal is divided into bearing fault impact area and impact attenuation area . After the impact in the signal is binarized by variable scale， it is regarded as the basic element of iteration and the VLZC index is calculated by ergodic search method . According to the 3σ prin⁃ ciple，the VLZC indexes of the inner and outer rings are given . The VLZC value range of damage degree and BP neural network are introduced to classify the damage degree intelligently . The results show that the new method can effectively reduce the noise， retain the periodic impact characteristics in the signal，suppress the non-impact components，improve the iterative calculation effi⁃ ciency，and effectively evaluate the damage degree of the inner and outer rings of rolling bearing .

Key words ： fault diagnosis；composite dictionary matching pursuit；variable scale Lempel-Ziv；binarization；BP neural network

作者简介：崔玲丽（1976—），女，教授，博导。电话：13691178029；E-mail：cuilingli@bjut .edu .cn。