耗能增效惯容系统的自适应权重粒子群优化

潘超 韩笑 张瑞甫 张雪 逯静洲

摘要：耗能增效是惯容减震系统的典型特征。为充分发挥此特性并同时满足减震性能需求，提出将惯容减震结构耗能增效程度最大化作为目标，并以性能需求作为约束条件进行减震参数寻优。基于随机振动理论推导惯容减震单自由度结构在白噪声激励下的解析解；建立最大耗能增效设计所对应等效约束优化问题的数学表达式。鉴于表达式的复杂性，采用鲁棒性好且便于实现的粒子群算法对问题进行求解。在粒子群算法中引入自适应惩罚权重考虑约束条件，并采用自适应调整的惯性权重提高求解效率。基于 Python 语言编制了自适应权重粒子群算法程序对惯容减震结构最大耗能增效设计问题进行求解。设计实例的求解过程体现了自适应权重粒子群算法对求解惯容减震结构优化设计问题的有效性，动力时程分析结果表明设计参数实现了预设的减震性能需求。

关键词：惯容系统；耗能增效；性能需求；约束优化；粒子群算法；自适应权重

中图分类号： TU318    文献标志码： A    文章编号：1004-4523（2022）05-1233-09

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.021

引言

地震是危及人类生命及财产安全的重大自然灾害之一，工程结构的破坏是地震灾害的主要表现形式。在结构中增设减震装置是降低地震响应、提高结构安全性的有效手段[1⁃2]。惯容系统是一种新型减震装置[3⁃4]，其两端点惯性、阻尼耗能增效的特性为结构减震控制提供了高效的解决方案。日本东北大学Ikago团队[5]率先展开惯容系统的减震研究，首次提出并研制了完整意义上的惯容系统，即调谐黏滞质量阻尼器（TVMD），继而给出了 TVMD 单自由度结构基于定点理论的参数设计方法。李超等[6]针对参数优化过程中忽略固有阻尼的问题提出了一种基于遗传算法的 TVMD 优化方法，以获得更合理的设计参数，同时也表现出智能算法在优化设计过程中的合理性。Faraj 等[7⁃8]提出利用冲击能量管理吸收冲击并存储在专用装置中来调节惯容器惯性质量的方法。罗建南等[9]提出了通过网络综合分析来系统地辨识最优惯容型减振器构型的方法。阎武通等[10]基于 H2优化理论对设置惯容系统的多自由度结构进行了参数优化方法。上述研究以最优控制为目标，忽略了与工程设计实际需求的联系。 Pan 等[11⁃12]认为惯容减震结构应以结构性能需求为直接设计目标，并基于随机振动理论提出兼顾控制效果与成本的惯容减震结构优化设计原则与方法。随后，Zhang 等[13]基于随机振动响应解析解发现了惯容系统的耗能增效原理，使惯容减震机理得到明确的物理阐释，并为惯容减震结构参数设计提供了更直观的思路。

基于耗能增效原理的设计方法涉及繁琐的随机振动响应表达式，采用常规数值优化算法时需要推导更繁琐的梯度表达式，且需要较准确的初始解，这给惯容减震结构的参数优化造成了一定的困难。鉴于此，本文采用鲁棒性好、原理简单且便于编程实现的粒子群算法对其进行惯容系统的最大耗能增效优化设计。本文以混联Ⅱ型惯容系统（TVMD）为研究对象[14]，首先基于惯容减震结构在白噪声激励下的随机振动响应解析解，给出了惯容减震结构最大耗能增效优化设计的数学描述，采用 Python 语言编制相应自适应权重粒子群算法的计算机程序，进行非线性约束优化问题的求解，最后通过设计实例分析验证了本文所提方法和所得参数的有效性。

1 惯容系统理论基础

1.1 单自由度惯容系统运动方程

单自由度结构在地震激励下的运动方程为：

式中  m，c，k 分别为单自由度结构的质量、阻尼和刚度；u，u̇，分别为结构质点的位移、速度和加速度；ag 为地面运动加速度。

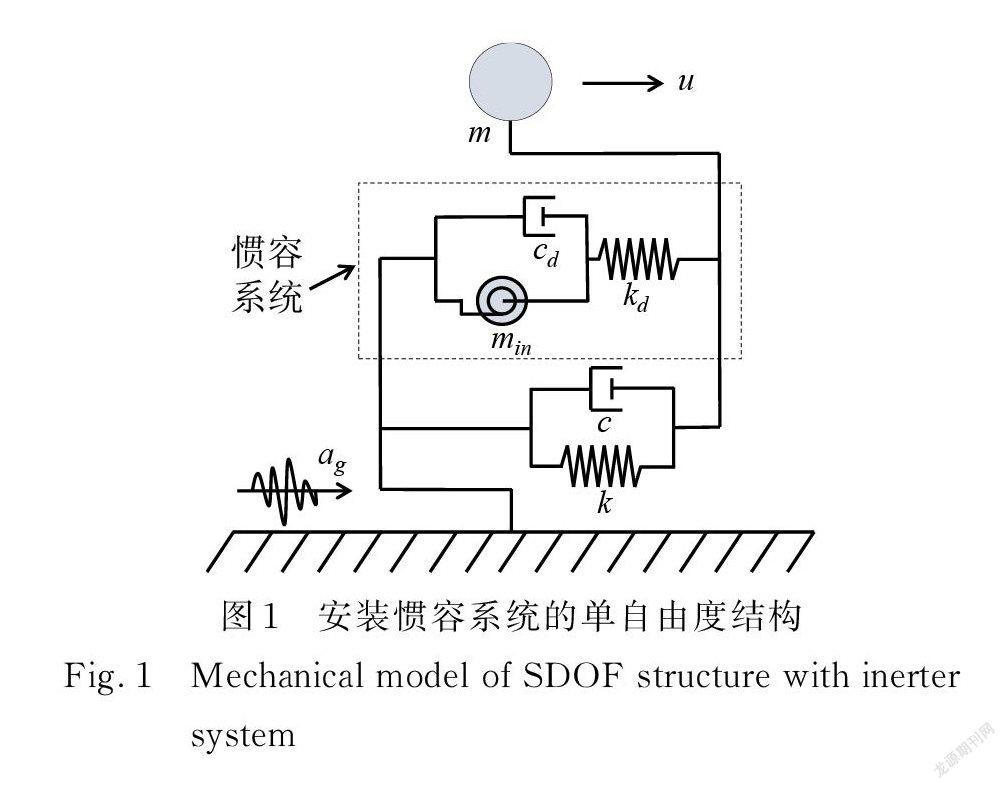
根据图1建立设置惯容系统的单自由度结构的运动方程为：

式中  min，kd，cd 为惯容系统中的惯容系数、弹簧刚度、阻尼器的黏滞阻尼系数，uin为惯容元件两端相对位移。

将式（2）中的等式左右两边同时除以质量 m可得

式中ω0，ζ分别为单自由度结构的自振圆频率和固有阻尼比；μ，κ，ξ分别为惯容系统的惯质比、刚度比和名义阻尼比。各参数的具体定义如下：

1.2 随机振动响应解析表达式

根据式（3）可推导出单自由度惯容减震结构位移响应的频域传递函数：

根据随机振动理论[15]，白噪声（功率谱密度为 S0）激励下，体系响应均方值为：

式中 H （ iω）为体系响应传递函数。

将式（5）代入式（7），可得惯容减震结构位移响应均方值的解析表達式为[12]：

基于随机振动响应表达式可定义惯容减震结构的减震比γ为[11]：

式中σu（2），0为未安装惯容系统的原单自由度结构的位移均方响应，表达式为：

将式（8），（12）代入式（11）即可得惯容减震结构随机响应减震比的具体表达式为：

1.3 惯容系统的耗能增效特性

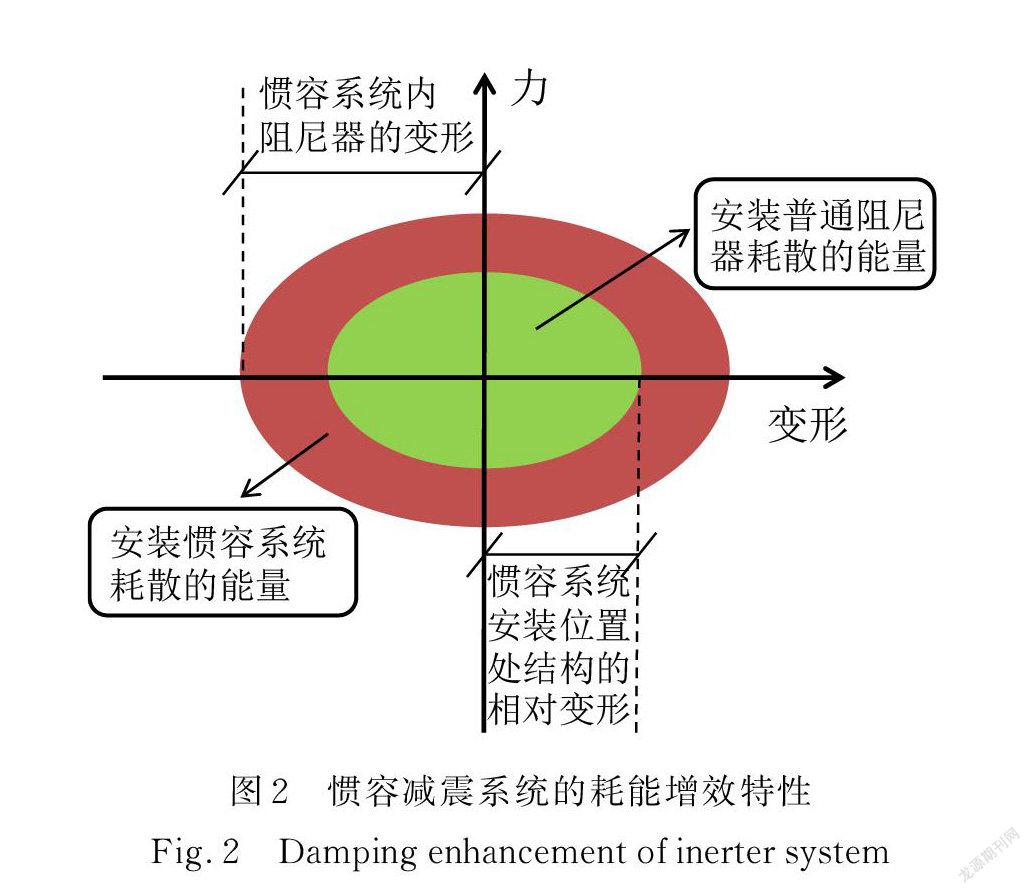
惯容系统耗能增效特性是指在动态荷载的激励下，惯容系统内部自由度的变形可大于其安装位置处主结构的相对变形[13]，从而高效地实现动力吸振与耗能减震。如图2所示，结构变形一定的条件下，惯容系统的耗能增效特性比普通阻尼器耗散更多的输入能量，进而降低动力响应。

为衡量耗能增效发挥的作用大小，文献[13]定义了惯容系统的耗能变形放大率α为：

基于随机振动响应解析表达式，求解白噪声激励下惯容系统耗能变形放大率α的具体表达式为[13]：

2 惯容系统的优化设计原则

为充分发挥惯容系统的耗能增效特性，本文以满足性能需求为前提，以耗能变形放大率最大化为原则进行惯容系统参数的优化设计。惯容系统优化设计问题表示为约束优化问题，即：

式中 f为优化目标函数；惯容系统耗能变形放大率α按式（15）计算；减震比γ按式（13）计算；γ t 为目标减震比，设计时可按下式确定[12]：

求解式（18）所述约束优化问题时，若采用经典的数值方法，由于公式繁琐、梯度计算不便，求解效果不够理想。考虑到粒子群算法原理简单且具有操作简单、容易实现、全局搜索能力强等优点，本文选择粒子群算法来对惯容减震结构进行参数寻优。

3 自适应权重粒子群算法

粒子群算法（Particle  Swarm  Optimization， PSO）是 Kennedy 和 Eberhart[16]提出的一种随机优化算法，其模拟的是鸟群飞行觅食的行为，通过鸟群集体之间的协作使群体达到最优的目的，适用于求解复杂的非线性优化问题。

标准粒子群算法优化存在易出现早熟收敛、寻优精度低等问题。大量研究结果表明，惯性权重是粒子群算法中平衡全局搜索能力与局部搜索能力的重要参数，采用自适应惯性权重策略计算惯性权重可改善算法的性能[17⁃18]。考虑到惯容优化设计问题的目标函数和约束条件都是非线性函数，故本文选用可以自动调节惯性权重的改进粒子群算法进行求解。

粒子群算法求解优化问题时，单个粒子代表一个可行解，粒子适应度值根据优化目标函数计算，种群中所有个体按一定规则不断移动以寻求最优解。粒子群中第i个粒子的移动规则为：

式中  t 为粒子移动时间步（t >0）；x  t ）为粒子i在t 时间步的位置向量，x i（b）est为粒子i在移动过程中的历史最优位置向量，xbest为整个种群的历史最优位置向量，v  t ）为粒子i在 t 时间步的速度向量；c1和 c2分别为粒子自身学习因子和社会学习因子；r1和 r2为0～1之间的随机数；w （ t ）为自适应惯性权重系数，可按下式计算：

式中wmax和wmin分别为惯性权重的最大和最小值，一般取值分别为1.0，0.3；Ps （ t ）为移动到更优位置处粒子所占比例，可按下式计算：

式中  n 为种群规模，即种群中的粒子数量；f （ x t ））为粒子 i 在 t 时间步的适应度值。惯容系统耗能增效优化设计问题属于约束优化问题，而粒子群算法本质上是一种无约束的搜索方法，因此本文采用惩罚函数法将惯容系统耗能增效优化设计问题转化为无约束优化问题后，再运用粒子群算法进行求解。引入惩罚函数后，惯容系统耗能增效优化设计问题的表达式为：

式中  h 為惩罚权重。由于合理的惩罚权重因具体问题而异，其数值不易确定，为提升算法的稳定性与收敛性，本文采用自适应变化的惩罚权重，即：

当使用粒子群算法求解惯容系统优化设计问题时，粒子适应度值按式（25）中优化目标函数计算，粒子位置向量 x  t ）为三维向量：

式中μ t ），ξi（ t ），κ t ）分别为粒子i在 t 时间步时惯容系统的惯质比、名义阻尼比、刚度比。

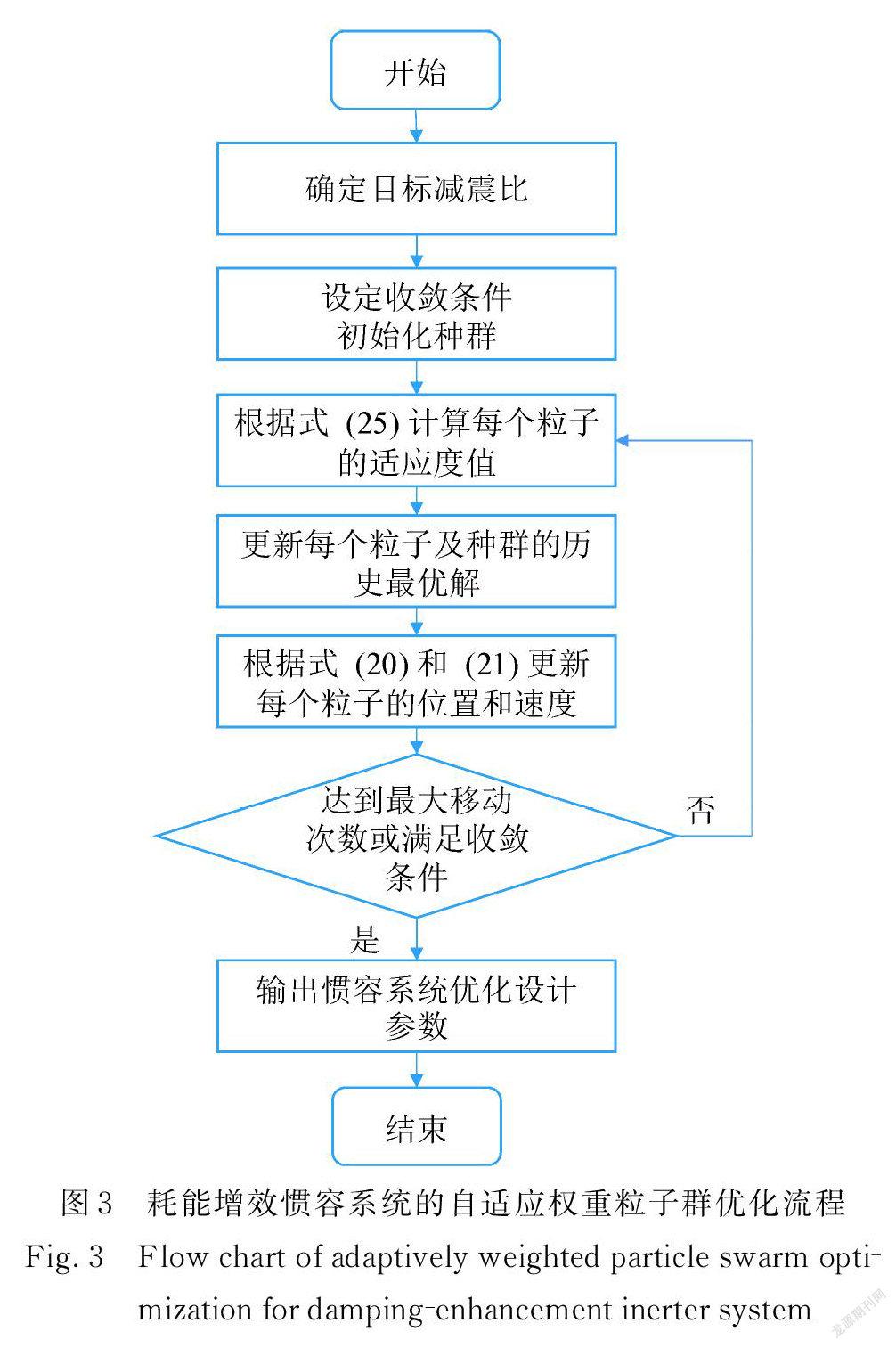
根据以上论述，可总结出采用自适应权重粒子群算法求解惯容系统耗能增效优化设计问题的流程（图3）如下：

（1）根据性能需求确定结构的目标减震比γ t；

（2）设定粒子群最大移动次数或收敛条件，选定种群规模 n，初始化每个粒子的位置向量 x  t ）（个体历史最优位置 x i（b）est亦按此初始化）和速度向量 v ; t ），根据式（25）计算每个粒子的适应度值，适应度最好的粒子所在位置即为种群的历史最优位置向量xbest；

（3）根据式（25）计算每个粒子的适应度值， f （ x t ））与历史最优位置相比适应度更好时，则相应更新每个粒子i的历史最优位置向量x i（b）est、种群的历史最优位置向量xbest；

（4）根据式（20），（21）更新各粒子的位置及速度；

（5）若粒子群达到最大移动次数或满足收敛条件则停止移动，否则，重复步骤（3）～（5）；

（6）取最终的xbest为最优参数，得到惯容系统关键参数μ，ξ，κ。

据此流程，本文采用 Python 编程语言编制了面向对象的计算机程序 APSOIS（Adaptive ParticleSwarm Optimization of Inerter System）用以求解惯容系统的参数优化问题。

4 算例分析

4.1  算例求解过程

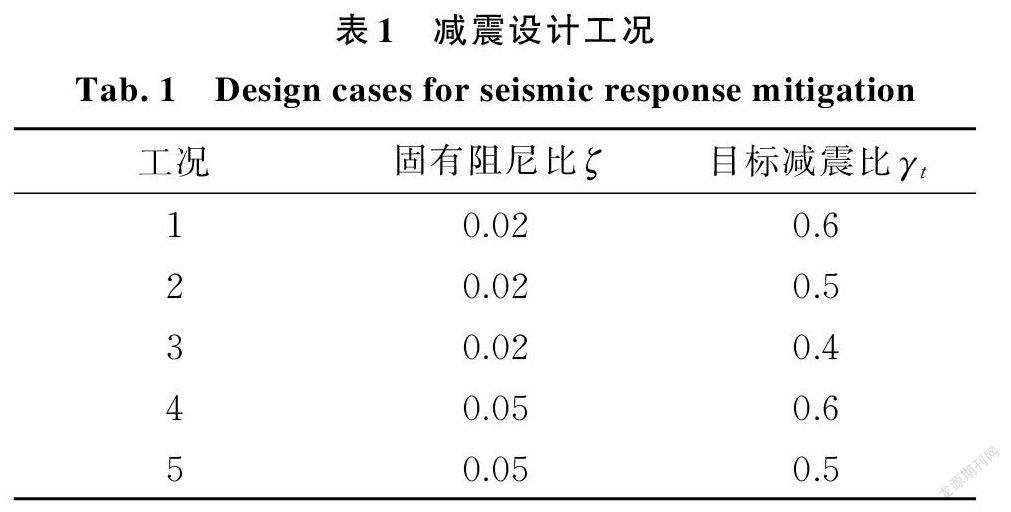
某单自由度结构，其质量 m =1500 t，刚度 k =192 kN /mm，自振周期 T =0.56 s 。拟通过设置惯容系统进行减震控制。

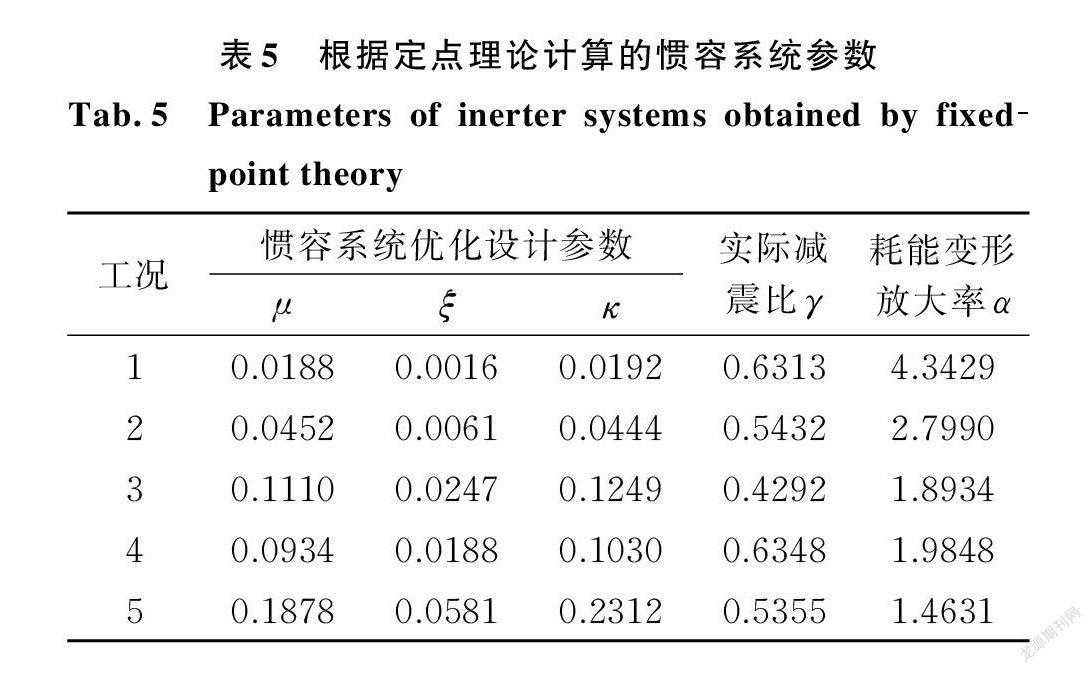
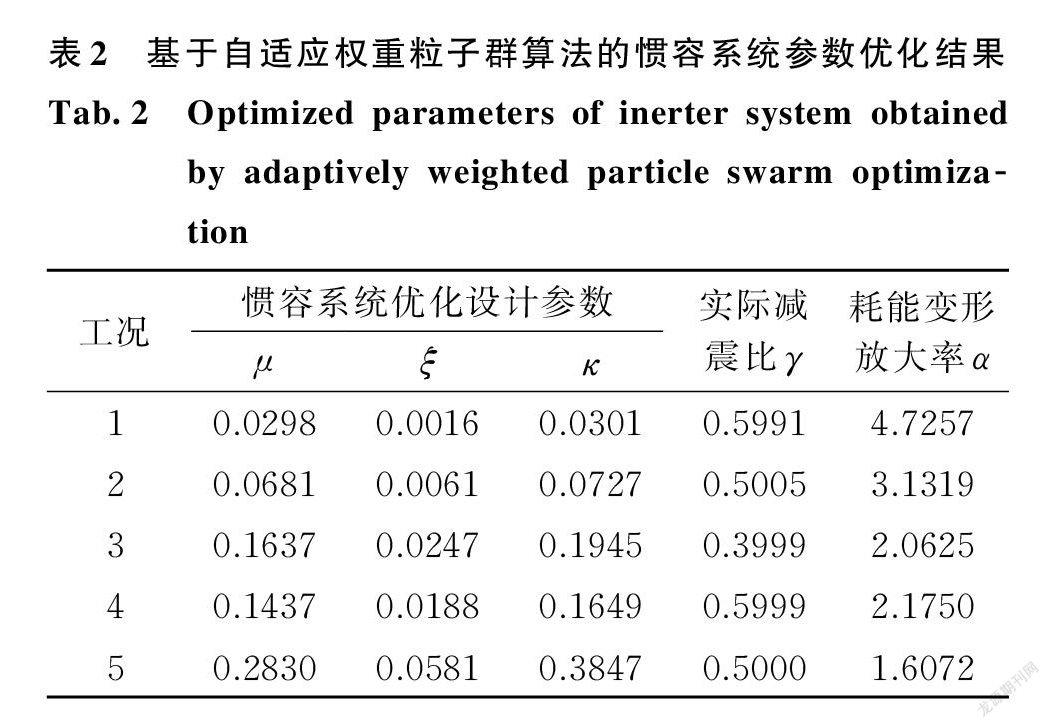
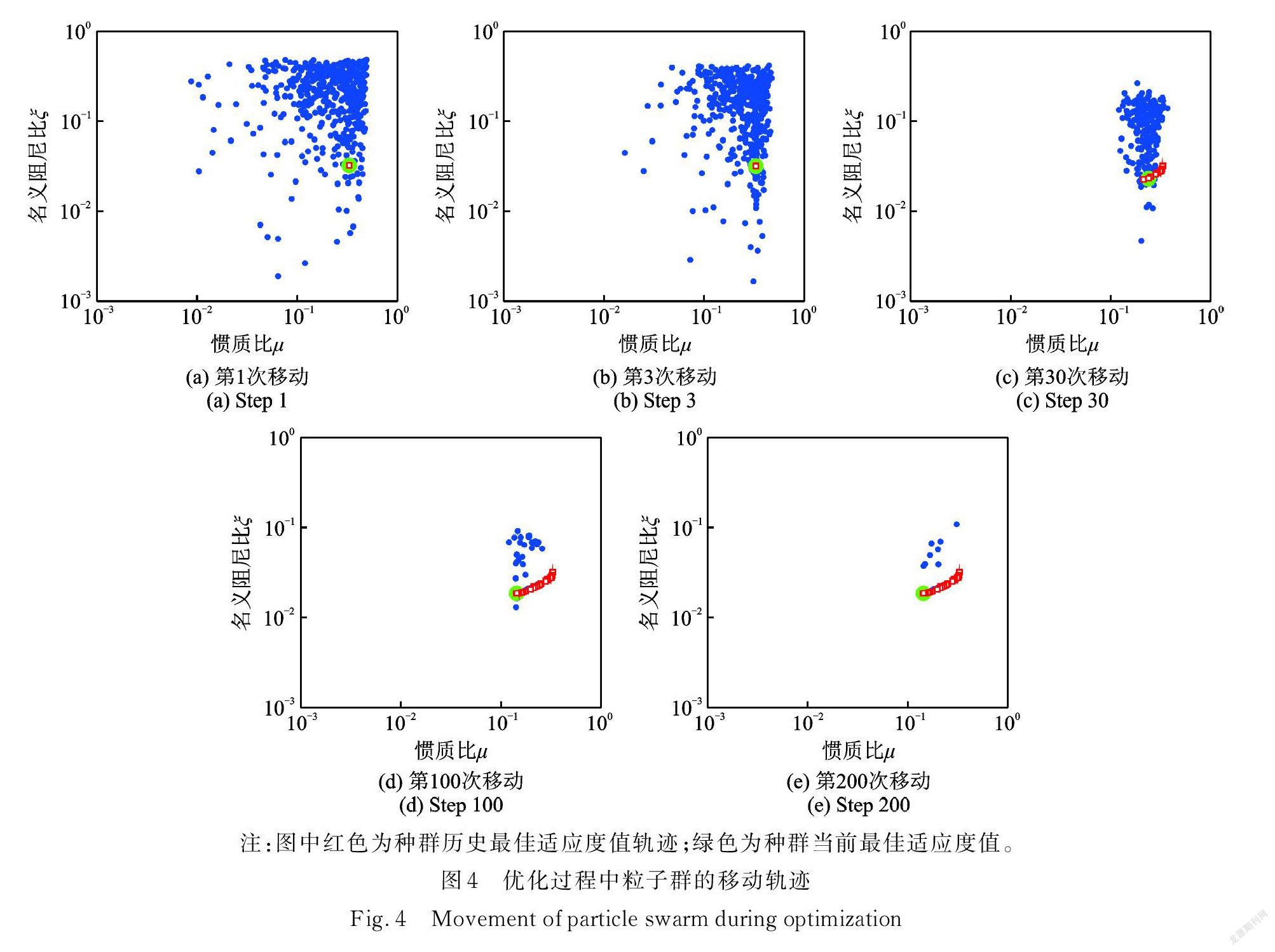
考虑固有阻尼比及目标减震比需求的不同，设置如表1所示5个设计工况。采用 APSOIS 程序求解惯容系统关键参数μ，ξ，κ的优化设计值如表2所示，同时给出各工况优化设计参数对应的实际减震比γ及耗能变形放大率α。为展示 APSOIS 程序求解惯容系统关键参数的过程，以工况4为例，AP ⁃ SOIS 求解最优适应度值的迭代轨迹如图4所示。

由图4可知，迭代开始时种群中各粒子随机分布，随着粒子群移动次数的增加，粒子群不断搜索到更好的适应度值，整个种群逐渐向最优解靠拢，最终大部分粒子都集中在最优解附近。

4.2  算法性能

为了解自适应权重粒子群算法的性能，考察了种群规模、惯性权重策略、惩罚权重策略对自适应权重粒子群算法求解过程的影响。

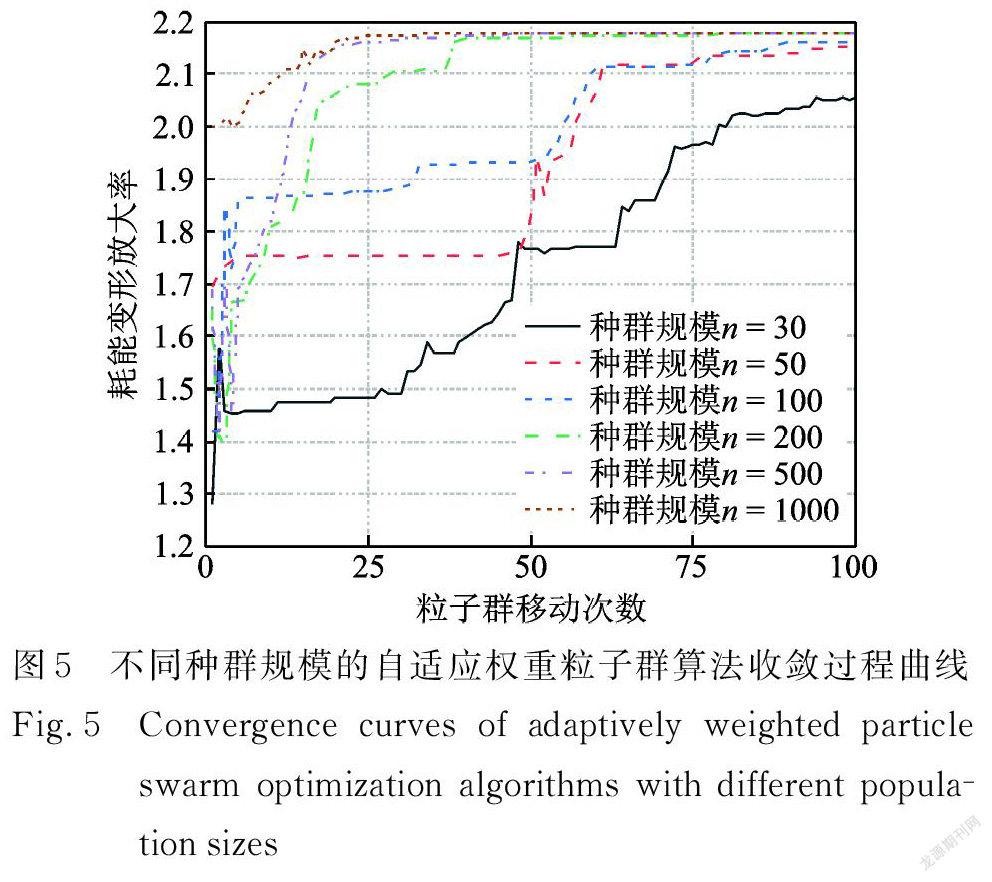
算法收敛曲线。由图可知，随着种群规模增大，种群可获得更好的初始最佳适应度值，且能以更少的移动次数收敛至最优解。由此，本文建议用自适应粒子群算法求解惯容系统优化设计问题时，可取种群规模200，最大移动次数100。

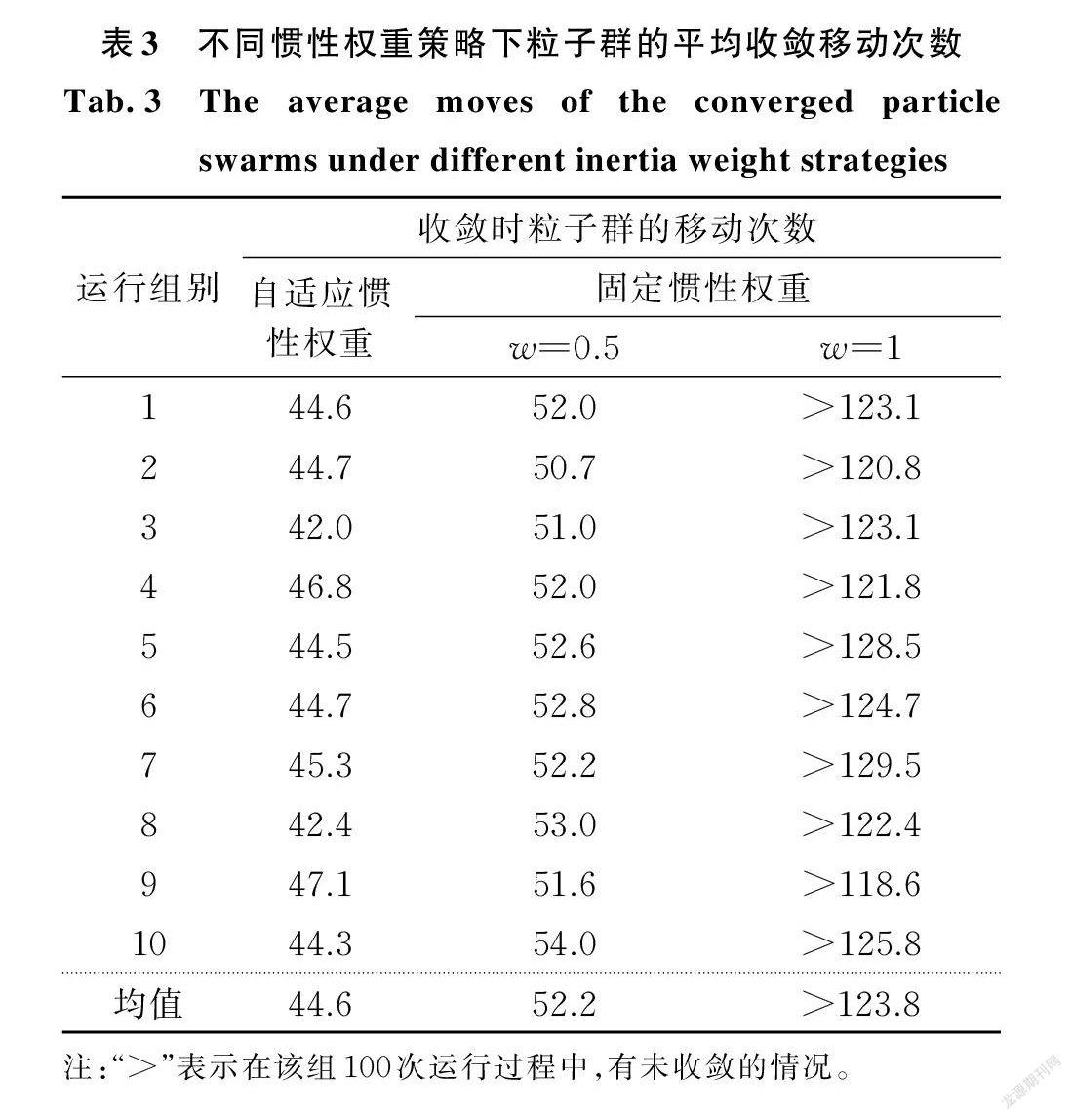
为验证自适应惯性权重策略的优势，以工况4为例，考虑不同的惯性权重策略，即自适应惯性权重、固定惯性权重（w=0.5，1），比较算法收敛时种群的移动次数。三种策略对应算法进行1000次求解（分为10组，每组100次），求解时设定粒子群种群规模为500，最大移动次数为200。收敛时每组所需平均移动次数如表3所示。

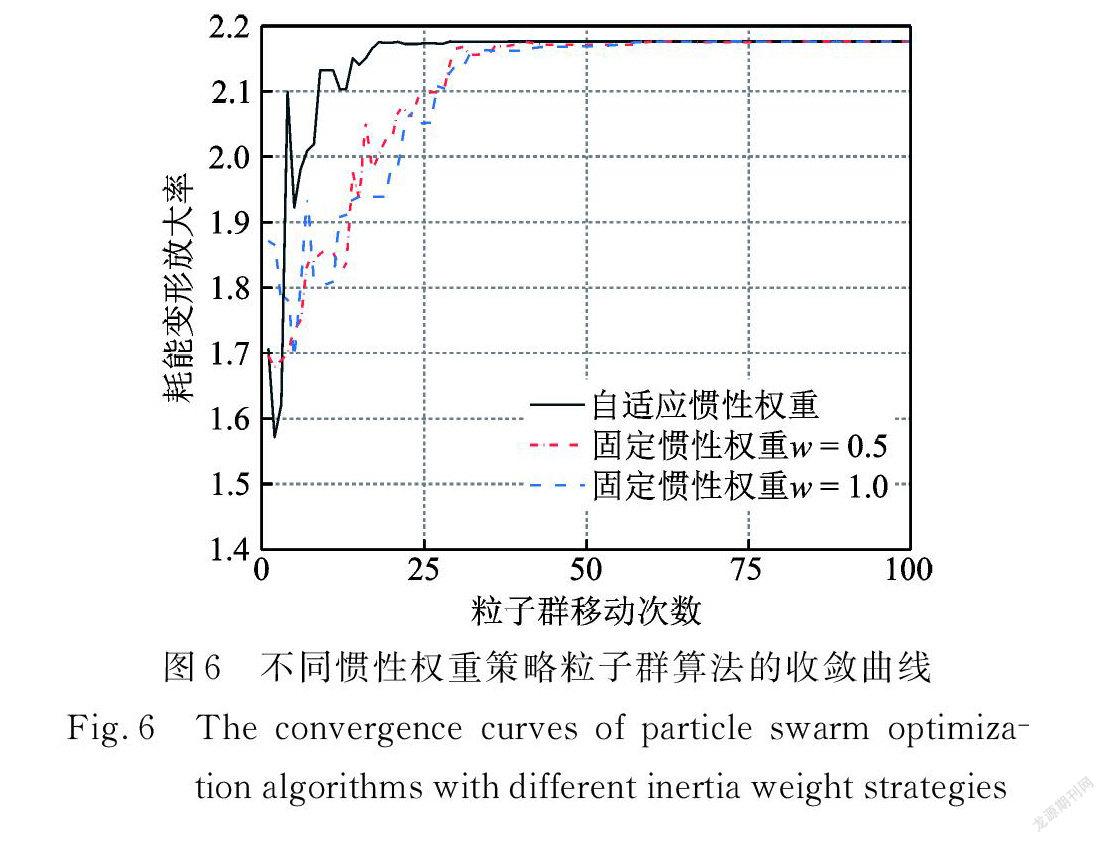
表3中每种策略对应的求解过程（成功收敛的情况）如图6所示。判断收敛成功的条件为：移动次数不超过最大移动次数的前提下，所得结果与种群规模1000、移动次数100次时结果之间相对误差小于0.1%。由表3及图6可知，自适应惯性权重策略下，算法的收敛移动次数小于固定惯性权重策略，表现出更强的求解能力。

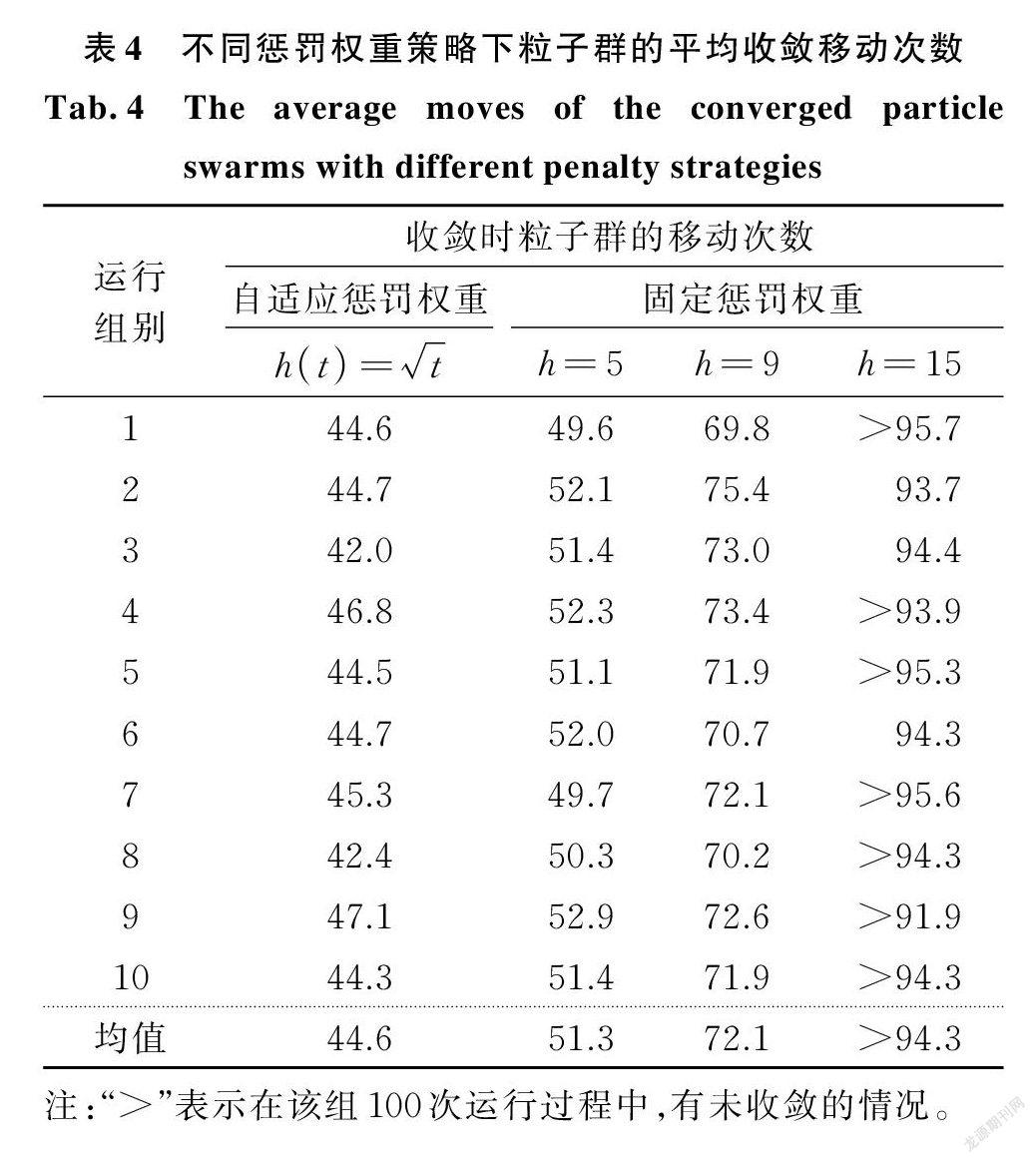
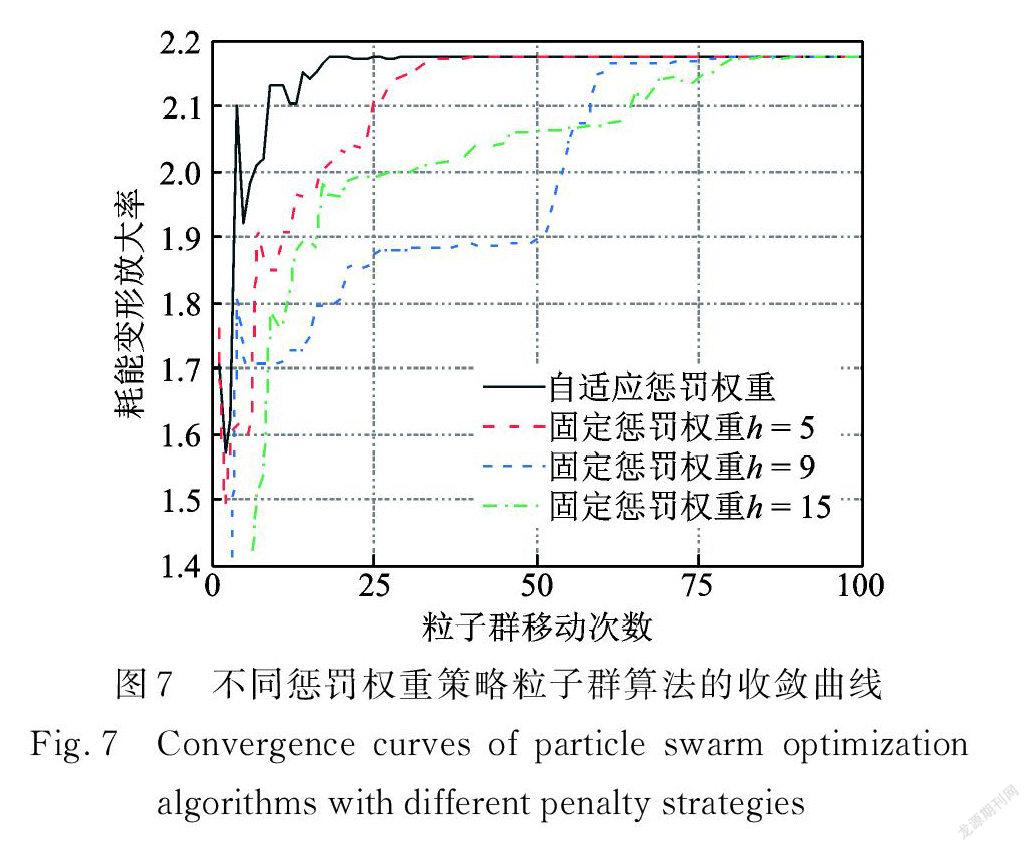
为验证自适应惩罚权重策略的优势，表4对比了自适应惩罚权重与固定惩罚权重为5，9，15时算法的收敛移动次数，相应收敛曲线如图7所示。由表4及图7可知，采用自适应惩罚权重策略的粒子群算法，其收敛移动次数小于固定惩罚权重策略的收敛移动次数。

4.3  减震性能

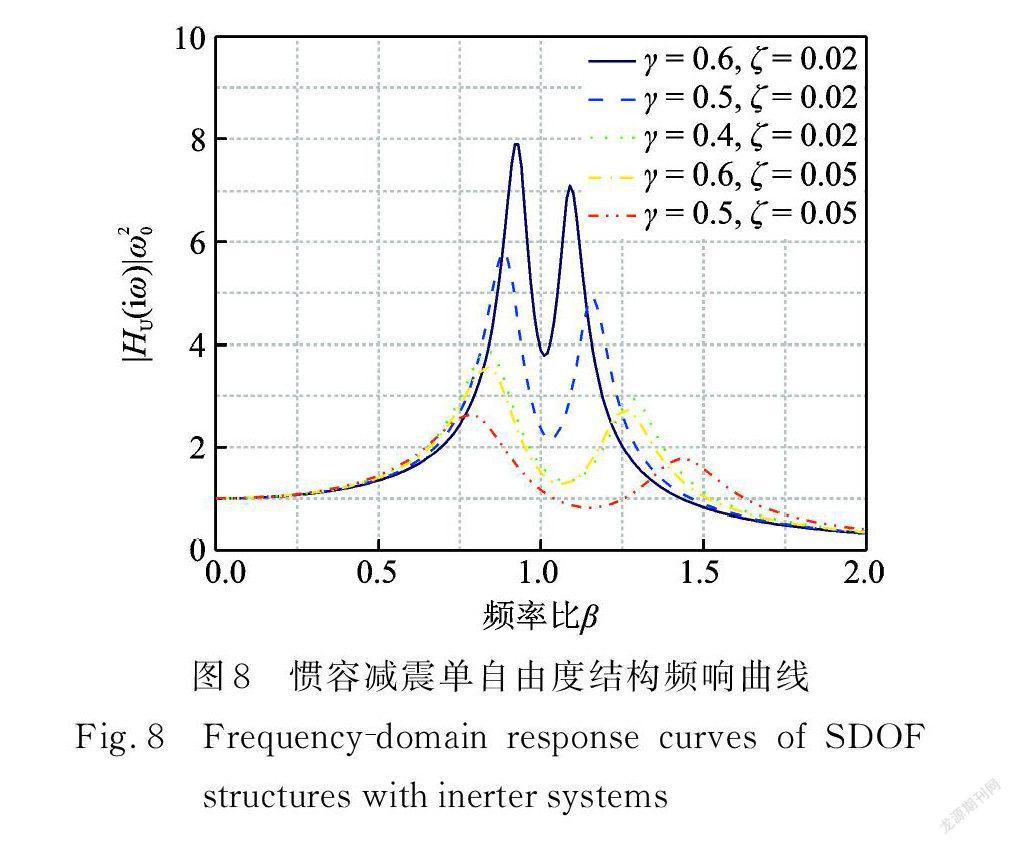
将表2自适应权重粒子群算法优化的惯容系统关键参数代入位移响应频响函数解析表达式（5）可得其频响曲线，如图8所示。基于自适应权重粒子群算法所得参数可以有效调谐并控制单自由度结构的地震响应。

为验证在有效控制地震响应的同时是否充分发挥惯容系统的耗能增效作用，将其与已有简化设计方法进行对比。根据Ikago等[19]提出的单自由度惯容减震结构设计方法，在已知惯容系统的μ后，κ和ξ可以通过下式计算：

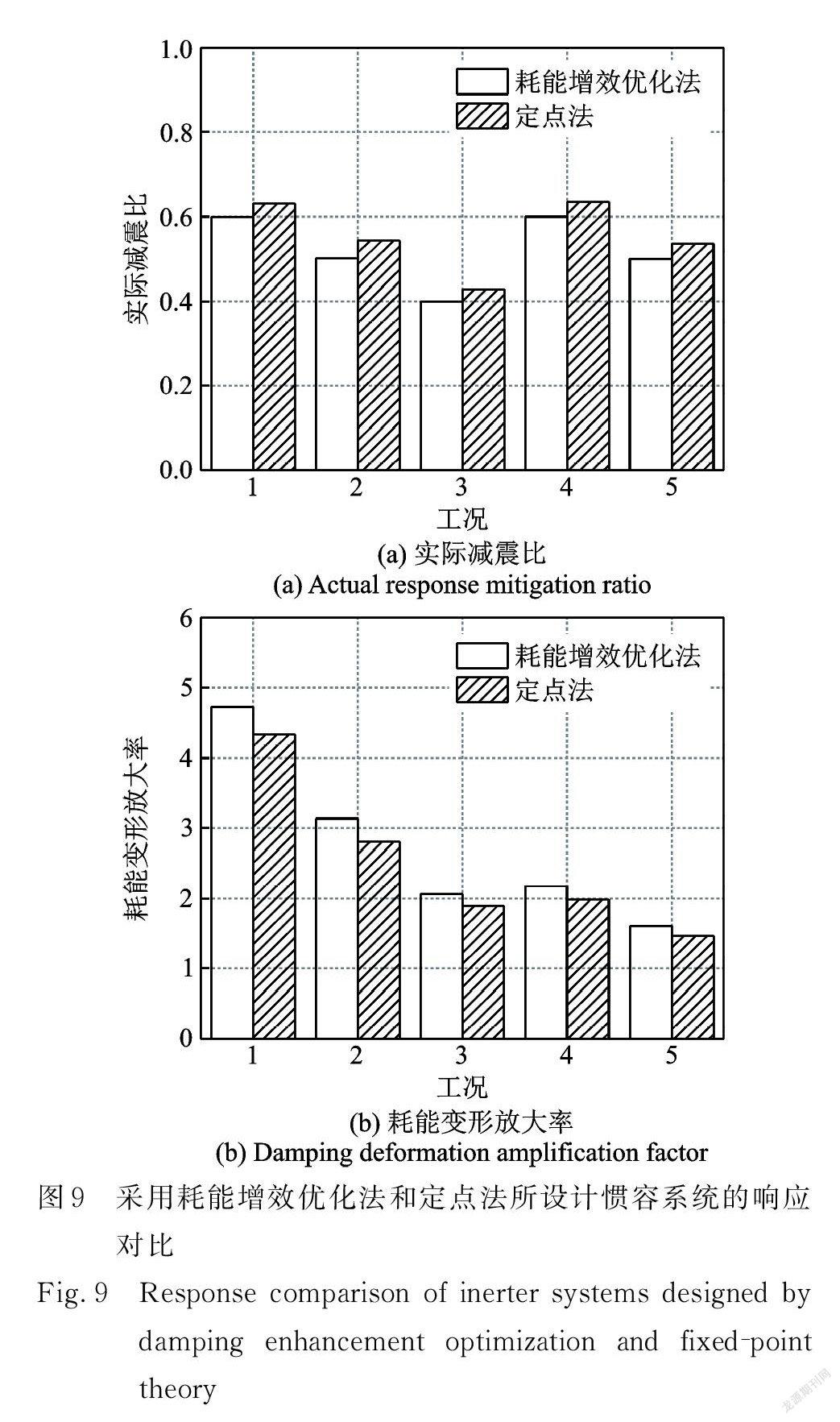
令式（29）中名义阻尼比ξ与表2中数值相等，可反算出对应的惯质比μ，进而根据式（28）计算出刚度比κ。这样可以在名义阻尼比ξ相同的条件下对两种方法的计算结果进行比较。使用Ikago方法得到的详细结果如表5所示。根据表2和5的数据，可得本文方法与Ikago方法在耗能增效程度和减震效果角度的对比情况如图9所示。对比可得，当二者名义阻尼比ξ一样时，在相同的工况下，所编自适应权重粒子群算法所得优化参数计算出的减震比γ与目标减震比γt 更相近，更符合所需减震结构的性能水准，具体大小对比如图9（ a ）所示。另外，如图9（b）所示，自适应权重粒子群算法所求得耗能变形放大率α均大于定点法所得耗能变形放大率，即在名义阻尼比一定的条件下，自适应权重粒子群算法优化的惯容参数能更大程度发挥惯容系统的耗能增效作用。通过与定点法对比证明了自适应权重粒子群算法优化参数设计的惯容减震结构能够充分发挥惯容系统的耗能增效作用。

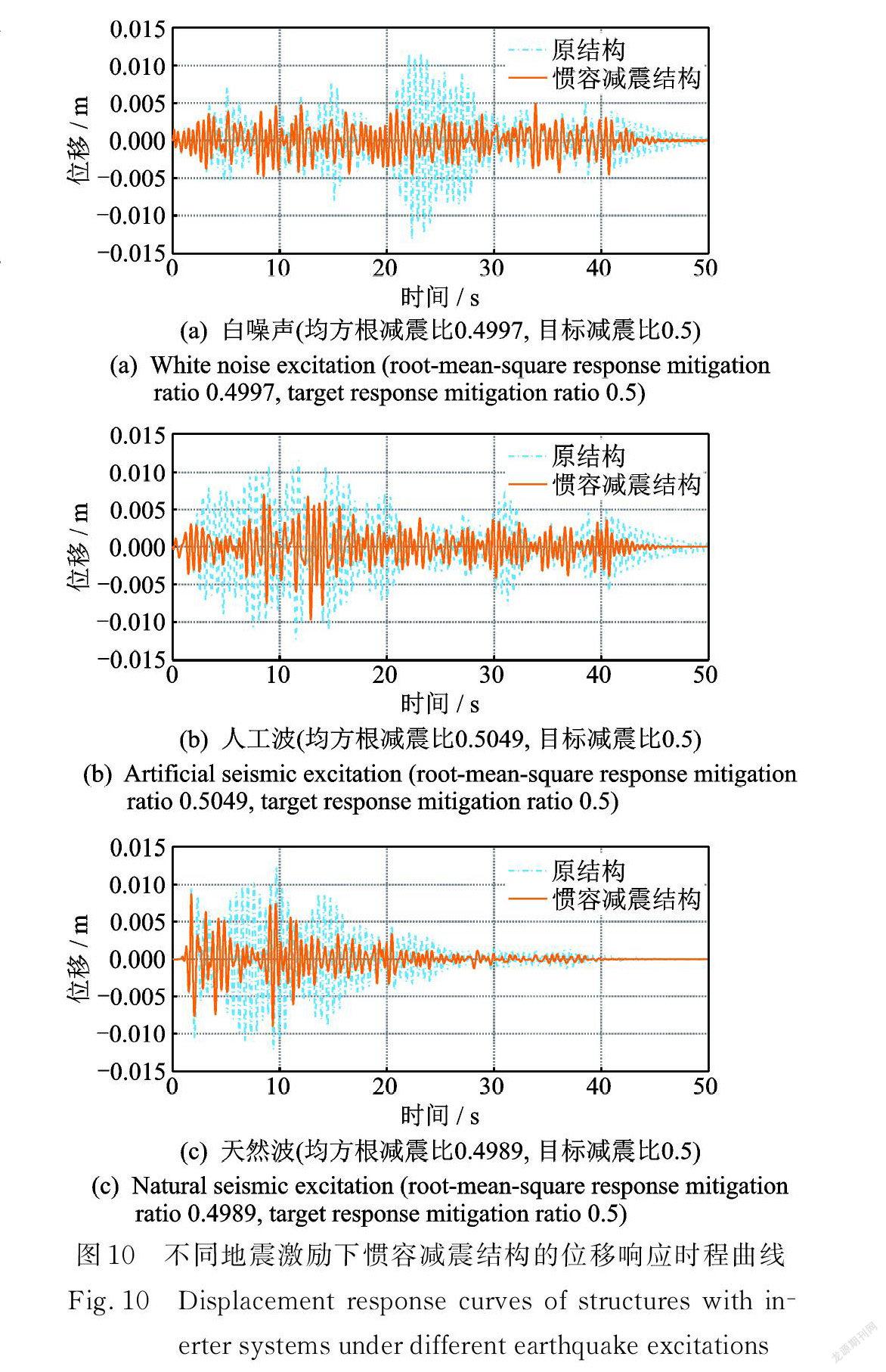
为直观展示慣容系统的减震效果，取工况2的设计参数，将惯容减震结构与原结构进行动力时程分析，通过输入具有不同频谱特性的地震动[14]（白噪声、人工地震波、天然波），计算其位移响应如图10所示。图 10显示在不同频谱地震动下惯容减震结构的位移响应均小于原结构的位移响应，且响应均方根减震比与所设定目标减震比均相近，证明了本文方法的有效性和设计参数的合理性。

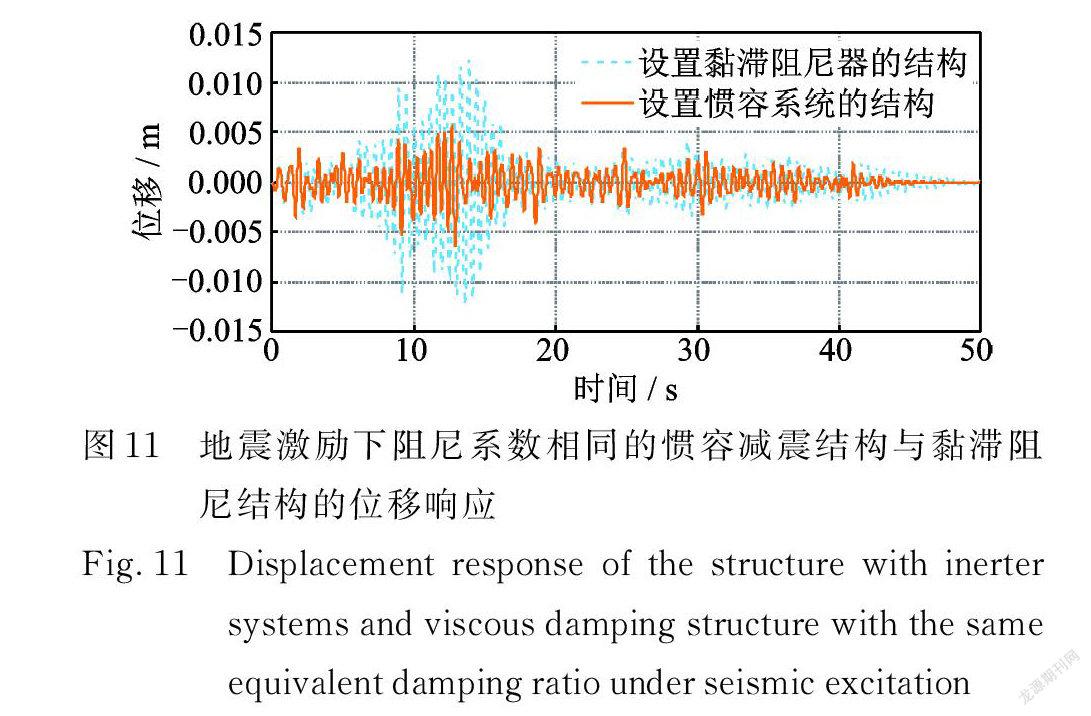
为体现惯容系统内阻尼器的减震效率，取工况2的设计参数，将惯容减震结构和单独设置黏滞阻尼器的减震结构（二者的黏滞阻尼系数相等）进行地震响应对比，结果如图11所示。由图可知，惯容减震结构的响应明显小于黏滞阻尼减震结构的响应，表现出更高的减震效率。

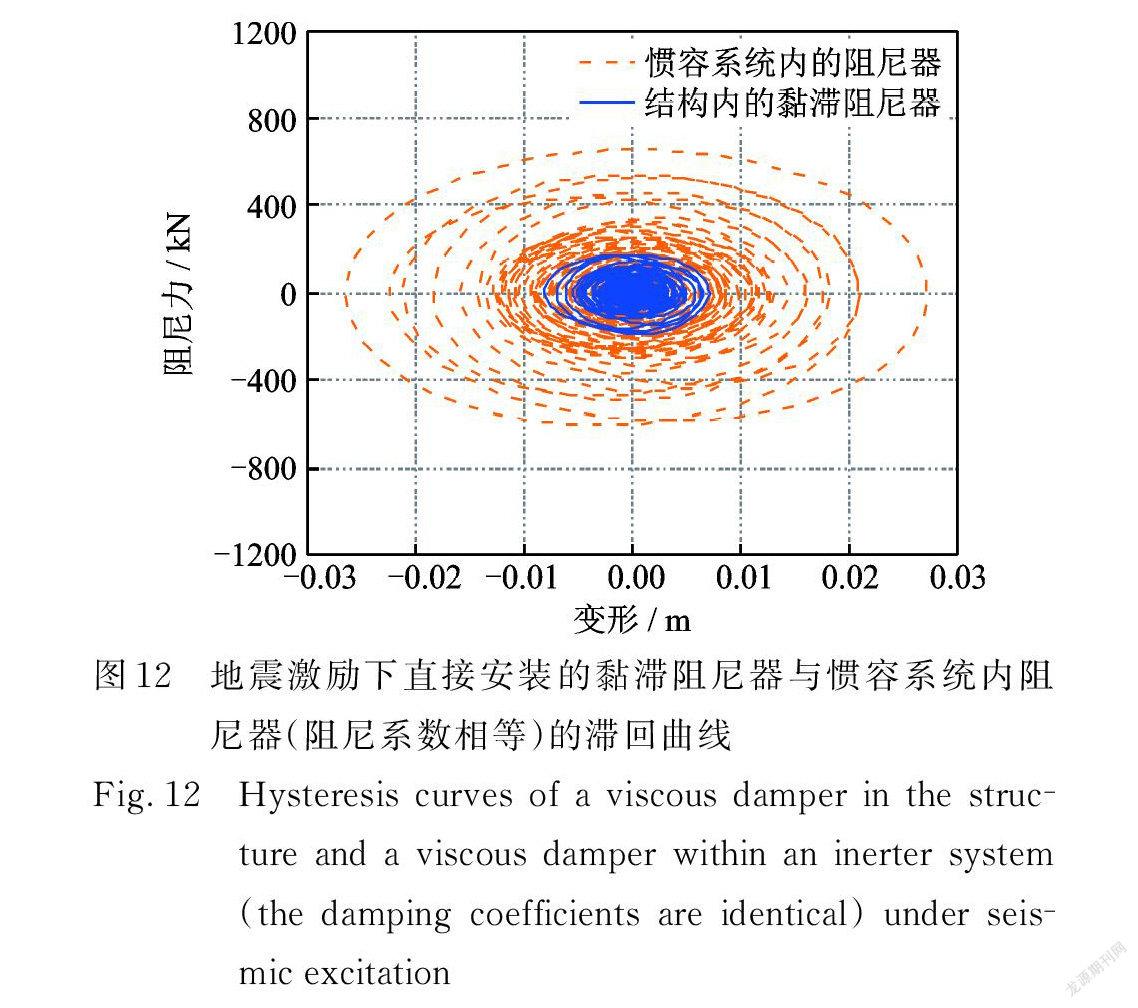
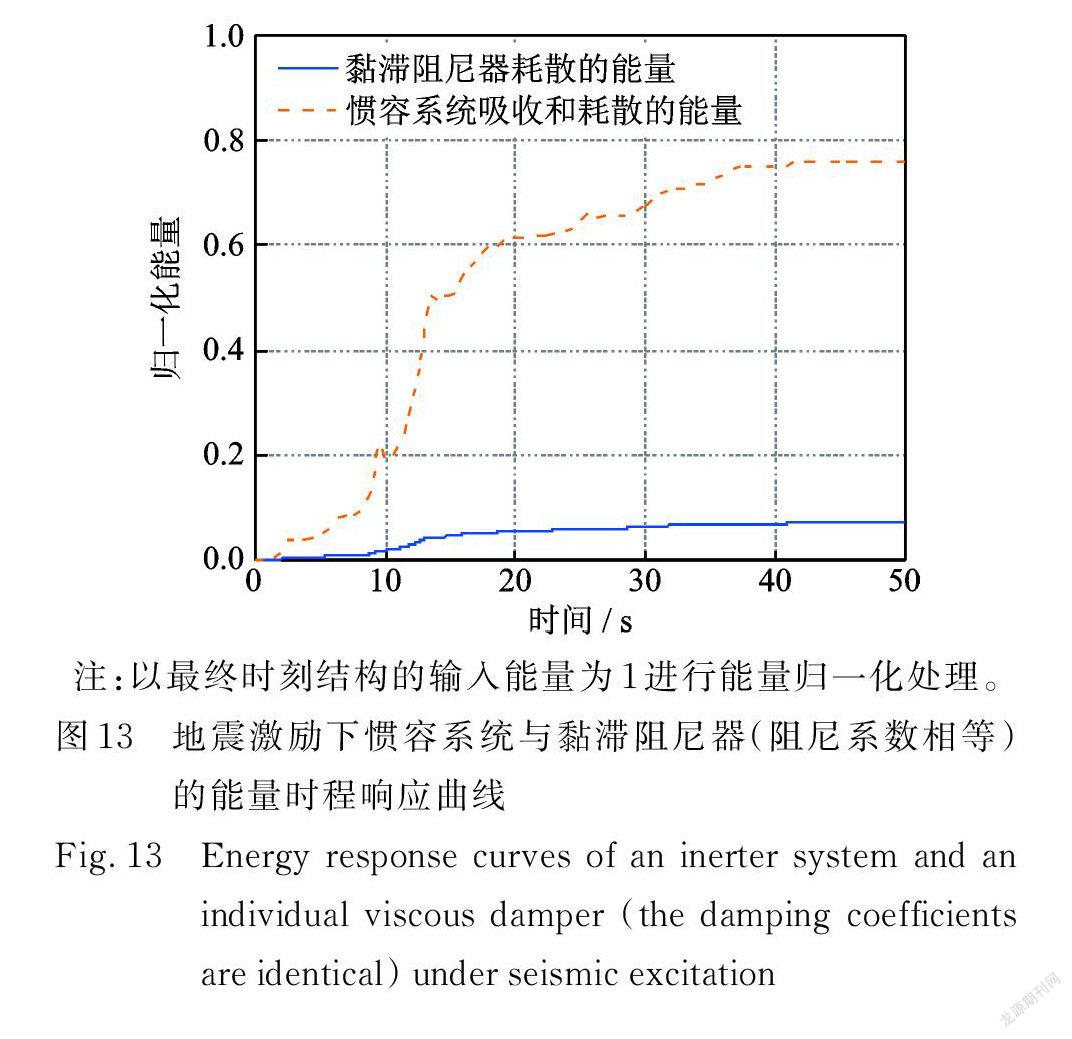
此外，本文还将惯容系统和黏滞阻尼器（二者黏滞阻尼系数相等）同时安装在结构中，以比较两者的耗能情况，结果如图12所示。通过滞回曲线的对比可知惯容系统内阻尼器的变形、阻尼力明显大于设置的黏滞阻尼器，其所耗散能量（滞回曲线所包裹的面积）也显著增加。图 13给出了相应的能量响应曲线，由图可看出在整个地震激励过程中，惯容系统吸收和耗散的能量都显著大于黏滞阻尼器（约10倍）。

5 结论

本文采用自适应权重粒子群算法实现了对惯容系统的耗能增效优化设计。结论如下：

（1）惯容减震系统的最大耗能增效优化设计问题可描述为约束优化问题，约束条件可采用惩罚函数的方式予以考虑。

（2）采用自适应权重粒子群算法求解惯容系统优化问题，无需复杂的数学理论，便于理解及编程实现。

（3）与经典粒子群算法相比，考虑自适应惯性权重和自适应惩罚权重的粒子群算法在求解惯容系统优化问题时具有更好的收敛性能。

（4）虽然本文仅对设置惯容系统的单自由度结构进行了讨论，但将本文方法框架中的响应求解过程和优化目标函数、约束条件等因素根据多自由度结构的特点进行调整后，即可用于多自由度惯容减震结构的优化，相关问题将在后续的研究中进一步探讨。

参考文献：

[1]  Saaed T E，Nikolakopoulos G，Jonasson J E，et al . Astate-of-the-art review  of structural control systems[ J ]. Journal of Vibration & Control，2013，21（5）：919-937.

[2]  Symans M D，Charney F A，Whittaker A S，et al . En ⁃ergy  dissipation  systems  for  seismic  applications ：cur⁃ rent  practice  and  recent  developments [ J ]. Journal  of Structural Engineering，2008，134（1）：3-21.

[3] 李壮壮，申永军，杨绍普，等.基于惯容-弹簧-阻尼的结构减振研究[ J ].振动工程学报，2018，31（6）：157-163.

Li Zhuangzhuang，Shen Yongjun，Yang Shaopu，et al . Study  on  vibration  mitigation  based  on  inerter-spring- damping  structure [ J ]. Journal  of  Vibration  Engineer? ing，2018，31（6）：157-163.

[4] 张瑞甫，曹嫣如，潘超.惯容减震（振）系统及其研究进展[ J ].工程力学，2019，36（10）：8-27.

Zhang  Ruifu， Cao  Yanru，Pan  Chao . Inerter  system and  state-of-the-art[ J ]. Engineering Mechanics ，2019，36（10）：8-27.

[5]  Ikago K，Saito K，Inoue N . Seismic control of single-degree-of-freedom  structure  using  tuned  viscous  mass damper[ J ]. Earthquake  Engineering & Structural  Dy⁃ namics，2012，41（3）：453-474.

[6] 李超，张瑞甫，赵志鹏，等.调谐黏滞质量阻尼器基于遗传算法的参数优化研究[ J ].结构工程师，2016，32（4）：124-131.

Li Chao，Zhang Ruifu，Zhao Zhipeng，et al . Optimum study  of tuned  viscous mass dampers based  on  genetic algorithm [ J ]. Structural  Engineers ， 2016， 32（4）：124-131.

[7]  Faraj R，Holnicki-Szulc J，Knap L，et al . Adaptive in⁃ertial  shock-absorber [ J ]. Smart  Materials &Struc⁃ tures，2016，25（3）：035031.

[8]  Faraj R，Jankowski U，Graczykowski C，et al . Can theinerter be  a  successful shock-absorber？The  case  of a ball-screw inerter with a variable thread lead[ J ]. Journalof the Franklin Institute，2019，356：7855-7872.

[9] 罗建南，景兴建，姜政.采用网络综合分析的最优惯容型减振器辨识方法研究[ J ].振动工程学报，2020，33（6）：1208-1215.

Luo Jiannan，Jing Xingjian，Jiang Zheng . Identification approach of optimum inerter-based absorbers using net⁃ work  synthesis [ J ]. Journal  of  Vibration  Engineering，2020，33（6）：1208-1215.

[10]阎武通，韩冰，文永奎.新型调谐黏滞质量阻尼器对斜拉桥的减震控制分析[ J ].土木工程学报，2016（S1）：66-71.

Yan  Wutong，Han  Bing ，Wen  Yongkui . Seismic  con ⁃ trol analysis  of cable-stayed bridge based  on tuned  vis⁃cous [ J ]. China  Civil  Engineering  Journal ，2016（S1）：66-71.

[11] Pan C，Zhang R，Luo H，et al . Demand-based optimaldesign  of  oscillator  with  parallel-layout  viscous  inerter damper[ J ]. Structural Control and Health Monitoring，2018，25（1）：e2051.

[12] Pan  C，Zhang  R . Design  of structure with  inertersys⁃tem  based  on  stochastic  response  mitigation  ratio [ J ]. Structural Control & Health Monitoring，2018，25（6）：e2169.1-e2169.21.

[13] Zhang R，Zhao Z，Pan C，et al . Damping enhancementprinciple  ofinerter  system [ J ]. Structural  Control  and Health Monitoring，2020，27（5）：e2523.

[14]潘超，张瑞甫，王超，等.单自由度混联Ⅱ型惯容减震体系的随机地震响应与参数设计[ J ].工程力学，2019，36（1）：132-140+148.

Pan Chao，Zhang Ruifu，Wang Chao，et al . Stochastic seismic response and design of structural system with se? ries-parallel-II inertersystem[ J ]. Engineering Mechan⁃ ics，2019，36（1）：132-140+148.

[15] Crandall S H M W D . Random Vibration in MechanicalSystems [M].   New  York： Academic  Press，1963：127-139.

[16] Kennedy  J ， Eberhart  R . Particle  swarm  optimization[C]. ICNN95-International Conference on Neural Net⁃ works . IEEE，1995：1942-1948.

[17]邓爱萍，王会芳.动态改变惯性权重的自适应粒子群算法[ J ].计算机工程与设计，2010（13）：3062-3065.   Deng Aiping，Wang Huifang . Adaptive particle swarm optimizationalgorithm  with  dynamically  changing  iner⁃tia weight[ J ]. Computer Engineering and Design，2010（13）：3062-3065.

[18]周俊，陈璟华，刘国祥，等.粒子群优化算法中惯性权重综述[ J ].广东电力，2013（7）：6-12.

Zhou Jun，Chen Jinghua，Liu Guoxiang，et al . Summa ⁃ ry on inertia weightin particle swarm  optimization algo⁃ rithm[ J ]. Guangdong Electric Power，2013（7）：6-12.

[19] Ikago K，Saito K，Inoue N . Seismic control of single-degree-of-freedom  structure  using  tuned  viscous  mass damper[ J ]. Earthquake  Engineering & Structural  Dy⁃ namics，2012，41（3）：453-474.

Adaptively weighted particle swarm optimization for damping enhanced inerter system

PAN Chao1，HAN Xiao1，ZHANG Rui-fu2，3，ZHANG Xue1，LU Jing-zhou1

（1.College of Civil Engineering，Yantai University，Yantai 264005，China；2.State Key Laboratory of Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China；3.Department of Disaster Mitigation for Structures，Tongji University，Shanghai 200092，China）

Abstract： Damping enhancement is the typical characteristic of the inerter system for seismic response mitigation . To give full play to this characteristic and meet the demand of seismic performance at the same time，it is proposed to maximize the degree of damp⁃ ing enhancement of the inerter system with the performance demand as the constraint condition during the decision of key parame ⁃ ters . The closed-form solution of a single-degree-of-freedom structure with an inerter system under the excitation of white noise is derived based on the theory of random vibration . The mathematical expression of the equivalent constrained optimization problem for damping enhancement maximization is established . Given the complexity of the expression，the particle swarm algorithm，a ro ⁃ bust and simple meta-heuristics method for numerical optimization，is used to solve the problem . The adaptively changed penalty weight is introduced into the particle swarm algorithm to consider the constraints，and the adaptively adjusted inertia weight is used to improve the efficiency for the search of the optimal solution . A computer program of the adaptively weighted particle swarm algo⁃ rithm is developed to solve the design problem of the inerter system for damping enhancement maximization . The design examples reflect the effectiveness of the adaptively weighted particle swarm  algorithm  in solving the optimization problem  of the structure with inerter system . And the dynamic time-history  analyses show that the structural damping performance demands are realized with the designed parameters .

Key words ： inerter  system；damping  enhancement；performance  demand；constrained  optimization；particle  swarm  optimization； adaptive weight

作者简介：潘超（1985—），男，副教授。电话：15953572531；E-mail：panchao@ytu .edu .cn。

通讯作者：张瑞甫（1980—），男，副教授。电话：13585903611；E-mail：zhangruifu@tongji .edu .cn。