S 变换引导变分模态提取的旋转机械故障诊断方法

郭远晶 金晓航 魏燕定 杨友东

摘要：针对信号变分模态分解（VMD）存在分解层数难以确定、目标模态难以选取的问题，介绍了一种信号分解方法——变分模态提取（VME），且提出了基于 S 变换（ST）与 VME 的旋转机械故障诊断方法。VME 将信号分解成两层——期望模态和残余信号，并基于一个新的准则：期望模态与残余信号之间具有最小的频谱重叠。为了使 VME 得到的期望模态包含充分的故障特征，采用 S 变换对信号进行处理，确定故障特征所在的频段，据此选取 VME 期望模态的中心频率初始值。为了从期望模态中提取出故障特征频率，采用平方包络谱（SES）对期望模态进行分析。仿真信号与实际振动信号的分析结果表明，所提出的 ST⁃VME 方法能够成功提取出有价值的期望模态和准确的故障特征频率，实现旋转机械故障诊断，且与 VMD 相比，ST ⁃VME 方法的目标性更强，实施更容易。

关键词：故障诊断；旋转机械；变分模态提取；S 变换；平方包络谱

中图分类号： TH165+.3；TH133.3    文献标志码： A    文章编号：1004-4523（2022）05-1289-10

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.027

引言

齿轮与轴承是旋转机械设备中的重要组成零件，其健康状态对于设备的正常运行具有重要影响。这些零件在工作中经常承受动态载荷甚至过载，容易产生各种类型的故障损伤，因此，对它们进行状态监测与故障诊断是非常有必要的。当齿轮或轴承出现损伤时，损伤处的接触刚度改变，再加上齿轮啮合或轴承元件滚动接触的不平顺性，会激励一系列的冲击。此时若旋转机械设备平稳运行，这些冲击则会在设备振动信号中以周期性的特征呈现，并对振动信号产生调幅⁃调频影响。冲击特征频率与设备的健康状态密切相关，不同的频率指示着设备不同的故障状态，如何从设备振动信号中提取出故障特征频率，是进行旋转机械故障诊断的关键。但由于旋转机械设备中通常包含多个旋转运动的零件，不同零件激励的振动相互耦合叠加，且振动信号会沿着从故障源头到振动传感器的传递路径衰减，因此，从传感器获取的设备振动信号中提取出故障特征并不是一件容易的事情。

目前，旋转机械设备故障特征提取的有效方法是信号分解，其中主要有经验模态分解（EMD）[1⁃3]、局部均值分解（LMD）[4⁃6]和经验小波变换（EWT）[7⁃8]等。这些分解算法各有优点，但也各自存在一些不足之处，如 EMD 和 LMD 存在端点效应、模态混叠、对噪声敏感等问题[9]，EWT 则存在抗噪性差、难以准确估计信号分量频率范围等问题[10⁃11]。鉴于此，Dragomiretskiy等提出了一种信号自适应分解方法——变分模态分解（VMD）[12]，该方法将信号分解成一系列具有不同中心频率的窄带本征模态函数，有着完备的数学理论支撑，且对信号采样要求不高、抗噪性好。VMD 凭借其优越的性能，在旋转机械设备故障诊断领域得到了广泛的研究与应用[13⁃16]。不足之处在于，VMD 在执行过程中需要预先设定模态分解的层数，然而，层数过多会导致过分解，产生虚假模态分量干扰；层数过少则会由于欠分解而导致模态混叠，难以提取目标模态[9] ；此外，VMD 结果中有多个模态，有用的目标模态也不太好选取。为此，2018年，Nazari 等提出了变分模态提取（VME）方法，用于从心电图中提取呼吸信号[17]。 VME 建立的基本理论与 VMD 相似，但 VME 将信号分解成两层——期望模态和残余信号，并基于一个新的准则：残余信号在期望模态的频带内具有尽量少的能量。需要指出的是，VME 在应用时需要预先确定期望模态的中心频率初始值，不然提取出的期望模态难以包含有用的信息。

在旋转机械振动信号处理的实际应用中，包含故障特征的期望模态通常位于某一特定频段内，只需将该层模态提取出来即可，其他层的模态则无需提取，从而避免虚假模态分量的干扰，降低计算量。因此，本文首先采用 S 变换对旋转机械振动信号进行时频表示，获取故障特征所在的频段，以此选取期望模态的中心频率初始值，然后利用 VME 提取出包含完整故障信息的期望模态，最后对期望模态进行平方包络谱分析，提取故障特征频率，实现旋转机械的故障诊断。

1 ST-VME 故障诊断方法

1.1 变分模态提取

假设输入信号 x （t）需要分解成两个信号：期望模态ud （t）和残余信号xr （t），即：

式中ud （t）为围绕中心频率ωd 的紧支撑函数，为了从 x （t）中完整地提取出ud （t），ud （t）与xr （t）需要满足以下准则：

（1） xr （t）与ud （t）之间具有最小的频谱重叠，即xr （t）在ud （t）频率范围内具有最小能量，特别是在中心频率ωd 处的能量应为0；

（2） xr （t）与ud （t）能够完全重构原始信号 x （t）。

因此，期望模态ud （t）的提取问题可以转化为一个受约束的最小化问题，表述如下：

式中α为平衡 J1和 J2的参数。J1用于衡量ud （t）围绕其中心频率ωd 的紧支撑性，定义为：

式中  ? t （⋅）表示关于 t 求偏导数，“*”表示卷积，δ（ t ）为狄利克雷函数，j=为虚数单位。

J2为衡量ud （t）与xr （t）之间频谱重叠程度的惩罚函数，定义为：

其中时域滤波器β（ t ）对应的频域滤波器 β̂（ω）在ω=ωd处取无穷大，使其对频率为ωd的信号成分具有无限的敏感性，而对频率远离ωd的信号成分具有类似 Wiener 滤波器的性能，则 β̂（ω）定义为：

为将上述约束最优化问题（2）转化为无约束最优化问题，引入二次惩罚项和拉格朗日乘子λ（t），构造增广拉格朗日函数：

根据 Parseval 时频域能量守恒定理：

式中 x̂ （ ω）为 x （ t ）的 Fourier 变换，将式（6）写成频域形式：

式中sgn （⋅）为符号函数； d （ω），x̂ r （ω）和（ ω）分别为期望模态ud （t）、残余信号xr （t）和拉格朗日乘子λ（t）的 Fourier 变换；⋅表示内积运算。

利用交替方向乘子法（ADMM），将最优化问题（2）转化为一系列迭代的子优化问题进行求解。在第 n +1次的迭代中，期望模态 d（n）+1可以通过下式进行求解：

根据参考文献[12]，将式（9）写成非负频率区间积分形式，并代入 β̂（ω）=1[α（ω-ω d（n））2]，得到：

经过代数运算，具体过程请参见文献[17]，可以得到期望模态 d 的更新表达式：

中心频率ωd 的更新表达式：

通过对偶上升法获得拉格朗日乘子的更新表达式：

式中τ为更新步长。

根据以上分析，得到 VME 算法的流程如下：

（1）初始化 d（1）和 1，n =0，估计中心频率ω d（1）初始值；

（2） n=n+1，整个算法开始循环执行；

（3）对所有的ω≥0，依据式（11）和（12）分别更新 d 和ωd；

（4）依据式（13）更新；

（5）给定精度值ε，若满足迭代终止条件：

结束整个循环，否则返回步骤（2）。

1.2  中心频率初始值选取

文献[17]指出，VME 期望模态的提取效果对其中心频率ωd 的初始值不太敏感，可以在一个比较宽的范围内选取。但旋转机械故障振动信号的分析结果表明，若要提取出包含故障特征的期望模态，ωd 初始值的选取必须在一个合理范围内，否则提取出的期望模态难以用于故障诊断。因此，本文采用 S 变换对旋转机械故障振动信号进行时频表示，确定期望模态中心频率ωd 的范围，并据此选取一个合适的ωd 初始值。

对于输入信号 x （t），其 S 变换定义为[18]：

式中ω（t，σ（ f ））为高斯窗函数，定义为：

控制高斯窗宽的标准差σ（ f）定义为与信号频率f成反比例的函数，即：

调整比例系数λ的值，可以在 S 变换时频谱中不同频段上获得相对优良的时频聚集性。S 变换分析窗的宽度与信号频率成反比，这使得 S 变换具有类似于连续小波变换的多分辨率特性，适合于非线性时变信号的处理与分析。

旋转机械的齿轮、轴承等零件出现故障损伤时，振动信号中包含有幅值与频率时变的冲击特征。利用振动信号的 S 变换谱可有效展示故障冲击特征[19]，指示冲击特征所在的频率范围，因而能够用于 VME 期望模态中心频率初始值的选取，以使获取的期望模态包含充分而完整的故障特征信息。

1.3 故障诊断实现方法

本文提出的 ST⁃VME 旋转机械故障诊断方法，首先对机械振动信号进行 S 变换，确定故障冲击特征所在的频率范围，从中选取一个频率值f0，得到 VME 期望模态中心频率ωd的初始值ωd0=2πf0；然后对振动信号进行 VME 处理，获得期望模态；最后对期望模态进行平方包络谱分析。

具体针对期望模态ud （t），其平方包络信号为：[20]

式中  ℋ{⋅}表示 Hilbert 变换，平方包络谱 USE （f）定义为uSE （t）幅值谱的平方，即：

式中 ℱ{⋅}表示傅里叶变换。

从平方包络谱 USE （f）中直接提取故障特征频率，实现旋转机械故障诊断。

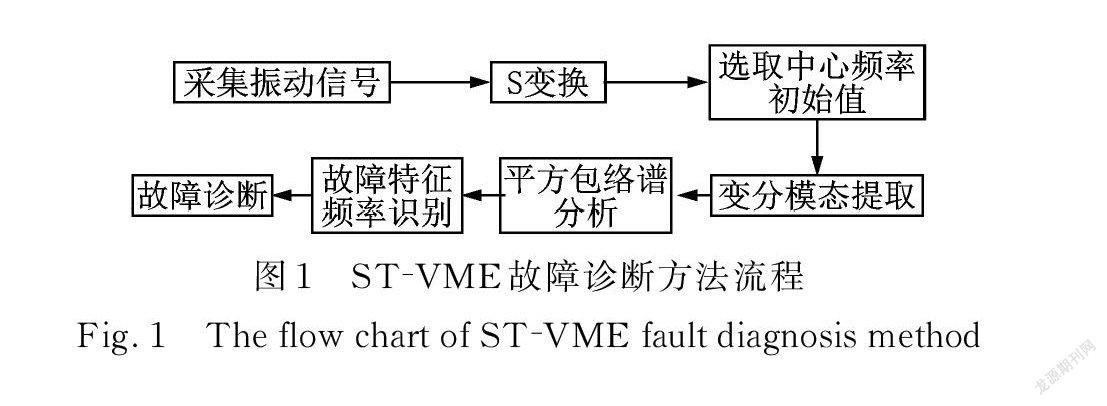
基于 ST⁃VME 的旋转机械故障诊断方法流程如图1所示。

2 仿真信号分析

仿真信号由齿轮局部损伤激励振动信号的数学模型生成。该信号模型由多次谐波、周期性的故障冲击特征与噪声信号组成，定义为：

式中sn （t）为噪声信号；fm为齿轮啮合频率；N 为谐波次数；X（ n ），φn，an （t）和 bn （t）分别表示第 n 次谐波的幅值、初相位、幅值调制函数和相位调制函数；K 和σ分别表示故障冲击特征的个数和幅值衰减指数；tk和 Pk 分别表示第 k 个冲击特征的出现时刻与最大幅值。

当齿轮平稳运行时，调制函数 an （t）和 bn （t）定义为：

式中fr为故障损伤齿轮的转频，An 和αn 分别表示第 n 次谐波幅值调制函数的幅值和相位，Bn 和βn 分别表示第 n 次谐波相位调制函数的幅值和相位。

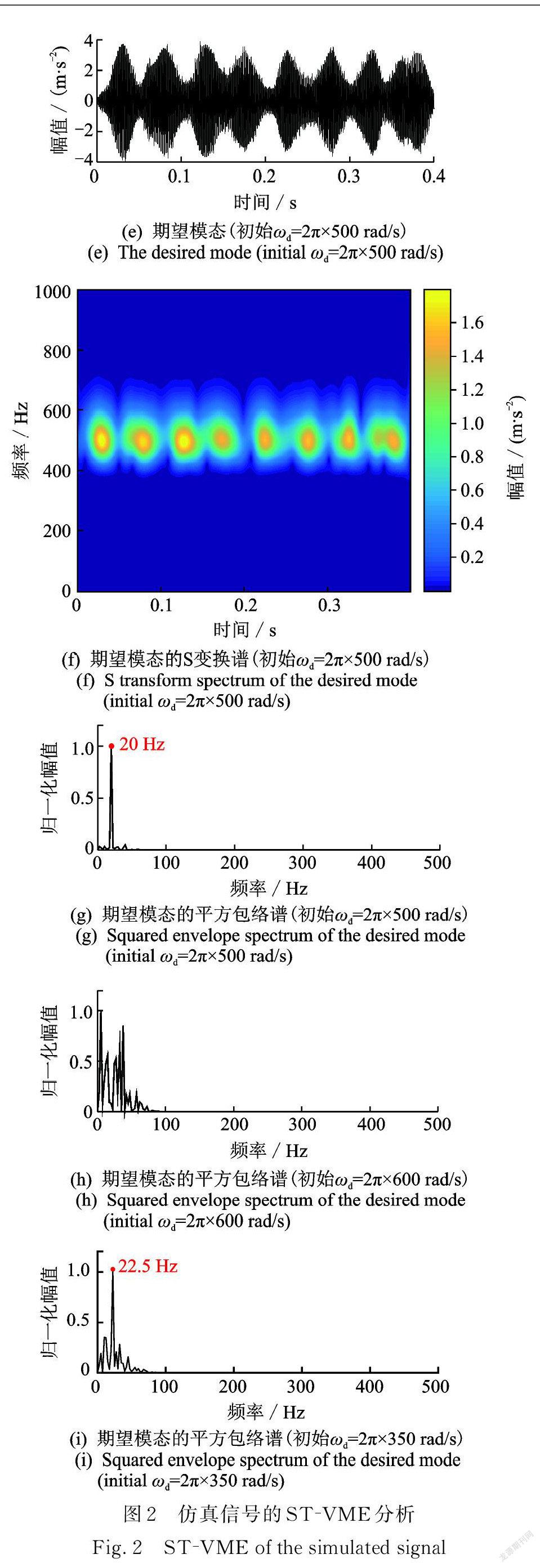
对于一对相互啮合的齿轮，假设局部损伤齿轮的齿数 z=25，转频fr =20 Hz，那么啮合频率fm =z ×fr =500 Hz 。为利用振动信号模型生成仿真振动信号，设定 N=1，X （ n ）=2，φn =π，An =0.25，Bn =0.5，αn =π，βn =π，σ=60π，信号采样频率fs =10 kHz，采样时间ts =0.4 s，数据长度 L=4000。令第1个冲击特征在 t1=0.025 s 时出现，由于损伤齿轮冲击振动所表现的故障特征频率与齿轮转频fr一致，因此在整个采样时间内，冲击特征的个数 K=[（ts -t1）×fr ]≈8；冲击特征的最大幅值 Pk （k=1，2，…，8）序列由均值1.3和标准差0.2的高斯随机序列生成。由此得到无噪的仿真信号如图2（ a ）所示，其 S 变换谱如图2（b）所示。往仿真信号中叠加高斯白噪声，使其信噪比为-8 dB，最终生成齿轮故障的仿真振动信號如图2（ c ）所示，由于信噪比很低，其中的故障特征完全被淹没，无法识别。

仿真信号的 S 变换时频谱如图2（d）所示，可以大致看出在频率500 Hz 处沿时间轴方向存在冲击特征，但受噪声干扰严重，规律不显著。将 VME 期望模态的中心频率初始值选取为2π×500 rad/s，提取出的期望模态如图2（ e ）所示，其 S 变换时频谱如图2（f）所示，可见该期望模态中包含了完整清晰的故障冲击特征，并表现出了显著的周期性。期望模态的平方包络谱如图2（ g ）所示，其中的幅值为归一化幅值，由各个频率成分的幅值除以幅值中的最大值得到，从图2（ g ）可见，其中的故障特征频率为20 Hz，与理论值一致。

事实上，从仿真信号的 S 变换谱图2（d）中可以看出，冲击特征所在的频段大致在400～550 Hz 之间，将中心频率初始值选取为该频段中的任意值， VME 得到的期望模态效果是一样的，而若将中心频率初始值选取在该频段之外，如2π×600 rad/s 或2π×350 rad/s，得到期望模态的平方包络谱如图2（h）或2（i）所示，则提取出的期望模态不能包含故障特征，无法提取出故障特征频率。由此可见，只要中心频率的初始值取在一个合理的范围内，VME 方法对中心频率是不敏感的，都能够提取出包含清晰完整故障特征的期望模态。当然，在实际应用中，并不需要确定中心频率初始值的具体范围，只需利用 S 变换谱选取一个合适的初始值即可。

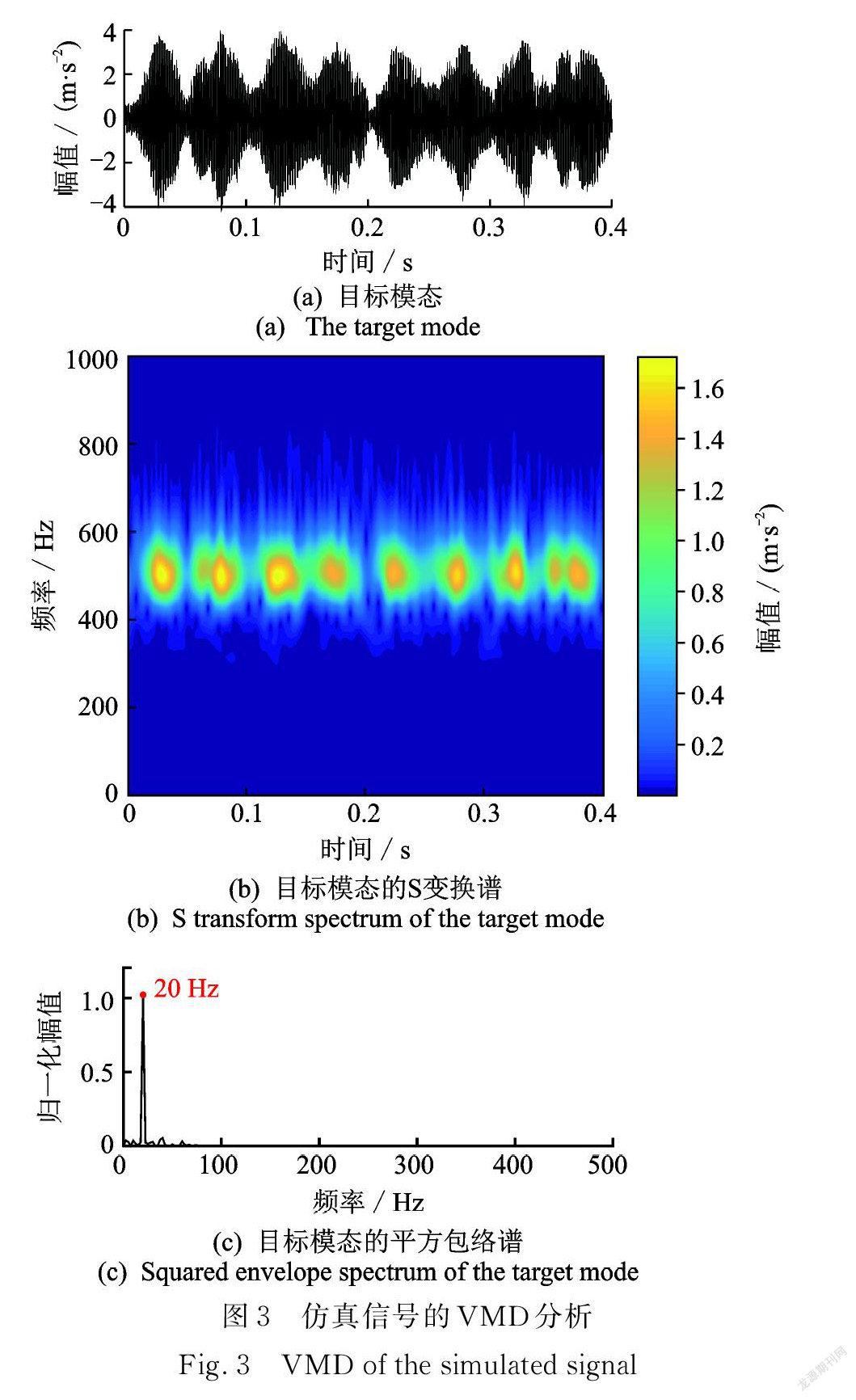
作为比较，采用 VMD 对仿真信号进行处理，其中分解模态的层数设为8，在分解结果中，包含故障特征的目标模态为第2模态，时域波形如图3（ a ）所示，S 变换谱如图3（b）所示，平方包络谱如图3（ c ）所示。通过对比可见，VME 得到的期望模态与 VMD得到的目标模态基本一致，都能够顺利提取出故障特征频率。不过在 VMD 中，合适的模态分解层数不太容易确定，分解结果中有用的目标模态也难以选取，而 VME 则不存在此问题。

此外，对比图2（ e ）与图3（ a ），并计算图2（ e ）所示期望模态与图2（ a ）所示无噪仿真信号之间的均方根误差，结果为0.4917，计算图3（ a ）所示目标模态与图2（ a ）所示无噪仿真信号之间的均方根误差，结果则为0.5148，由此可见，VME 提取的期望模态要比 VMD 提取的目标模态更干净，噪声更少。

从时域波形上来看，相比原始无噪的仿真信号， VME 提取的期望模态和 VMD 提取的目标模态中均存在一定程度的变形，这是由 VME 和 VMD 算法本身所决定的，并不影响平方包络谱中故障特征频率的提取。

3 实际振动信号分析

3.1  试验台齿轮振动信号分析

齿轮箱试验台如图4（ a ）所示，其用于模拟风力发电机以及齿轮箱故障诊断研究。试验研究对象选为一级传动的平行轴增速箱，增速比为2.45，其中的小齿轮上加工有轮齿局部断裂的故障损伤，如图4（b）所示。在运行试验中，驱动电机的转速设为700r/min，加载电机的载荷设为3 N·m，测得平行轴增速箱的输出转速为1347 r/min，计算得到小齿轮的故障特征频率为22.45 Hz，振动信号采样频率设定为5.12 kHz。

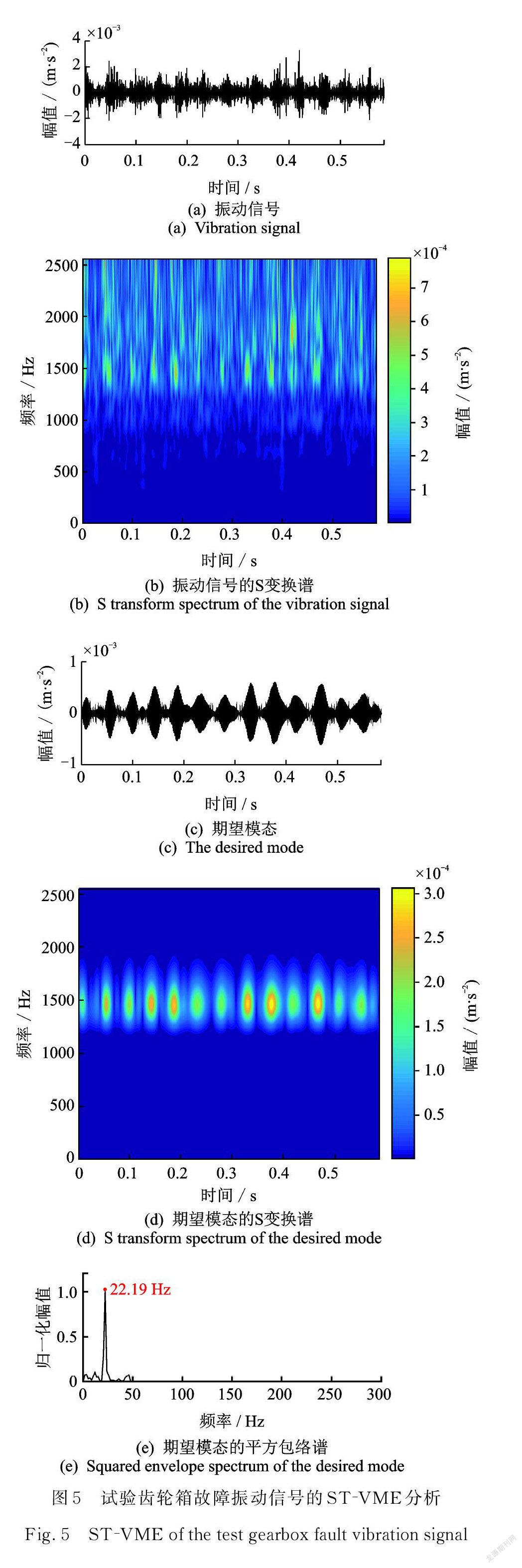
从平行轴增速箱上采集一段数据长度为3000的振动信号，时域波形如图5（ a ）所示，可见其中包含有一些故障冲击特征。振动信号的 S 变换谱如图5（b）所示，可以大致看出在1450 Hz 左右位置处，沿时间轴方向出现间歇性的冲击特征，不过由于噪声干扰比较大，冲击特征并不显著。将中心频率初始值选取为2π×1450 rad/s，VME 获得的期望模态如图5（ c ）所示，S 变换谱如图5（d）所示，可见该期望模态包含了清晰完整的故障冲击特征，有效抑制了噪声干扰。期望模态的平方包络谱如图5（ e ）所示，其成功提取出了试验齿轮的故障特征频率22.19 Hz。

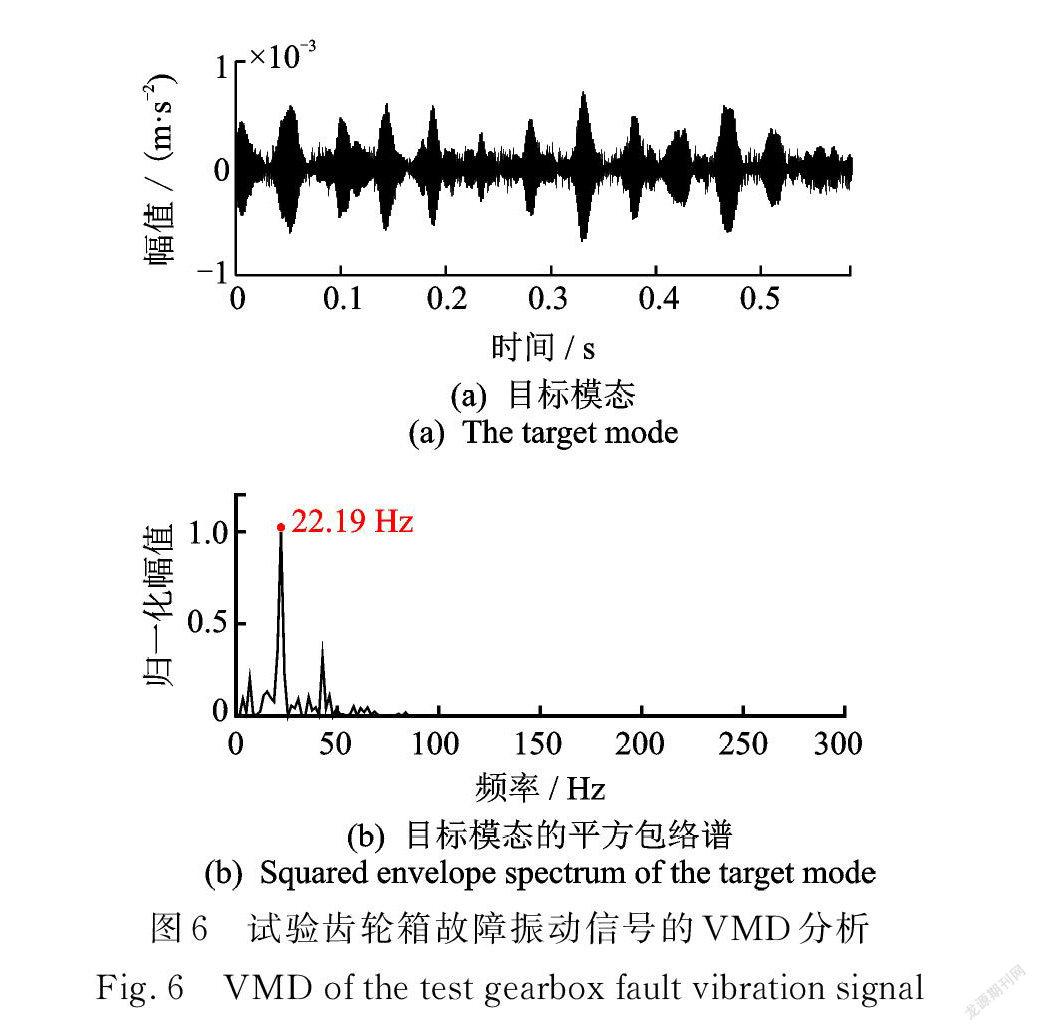
采用 VMD 方法对该组振动信号进行处理，其中分解模态层数设为5，分解結果中包含冲击特征的目标模态为第4模态，如图6（ a ）所示，其平方包络谱如图6（b）所示，可见 VMD 也能够提取出试验齿轮的故障特征频率。不过在 VMD 的执行中，模态分解的层数可能需要多次尝试才能合理确定，有用的目标模态也需要正确地选取。此外，VMD 提取出的目标模态中仍有较大程度的噪声，效果没有 VME 获取的期望模态好。

3.2  风力发电机齿轮振动信号分析

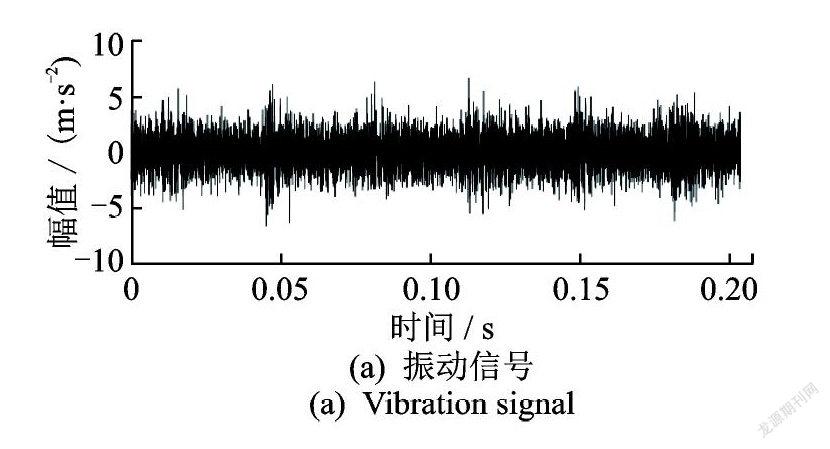
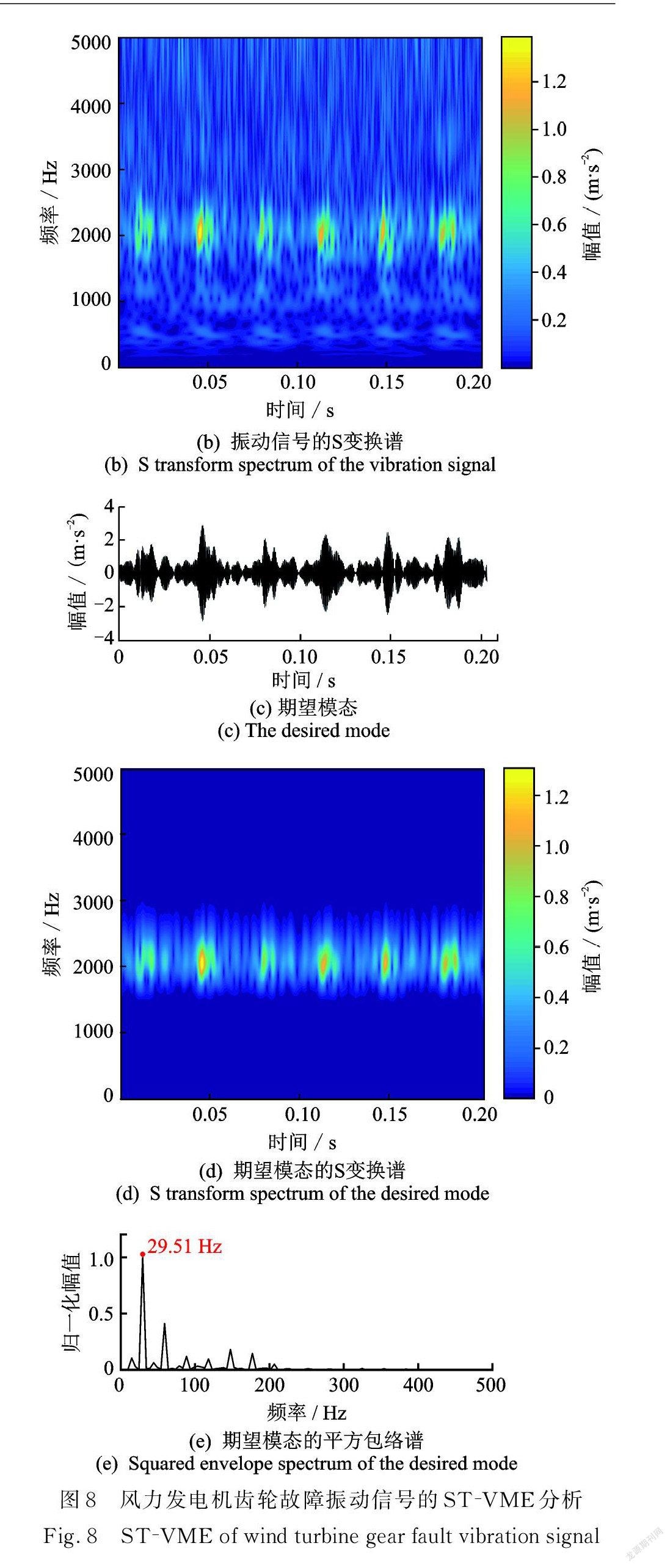
该组振动数据来源于一台风力发电机，其齿轮箱中的一个小齿轮发生了轮齿断裂故障损伤，如图7所示。该小齿轮的参数如下：齿数 z=32，转速 n=1770 r/min，转频fn =29.5 Hz，故障特征频率fg =29.5 Hz 。设定振动信号采样频率fs =97656 Hz，采集到一段长度为19854的振动信号如图8（ a ）所示。该振动信号的 S 变换谱如图8（b）所示，可以看出大约在2000 Hz 的位置处，出现规律性的冲击特征，因此选取2π×2000 rad/s 作为中心频率初始值，VME 提取的期望模态如图8（ c）所示，其 S 变换谱如图8（d）所示，可见其中显著的故障冲击特征，噪声得到了很好地抑制。期望模态的平方包络谱如图8（ e）所示，风力发电机齿轮的故障特征频率29.51 Hz 被顺利提取出来。

采用 VMD 对该组振动信号进行处理，经过尝试，模态分解的合理层数为5，分解结果中有用的目标模态为第1模态，如图9（ a ）所示，其平方包络谱如图9（b）所示，可见 VMD 也能够提取出包含完整故障特征的目标模态和风力发电机齿轮的故障特征频率，不过通过对比可以发现，VMD 得到的目标模态中仍包含有较多的低幅值高次谐波，不如 VME 的期望模态纯粹。

3.3  轴承振动信号分析

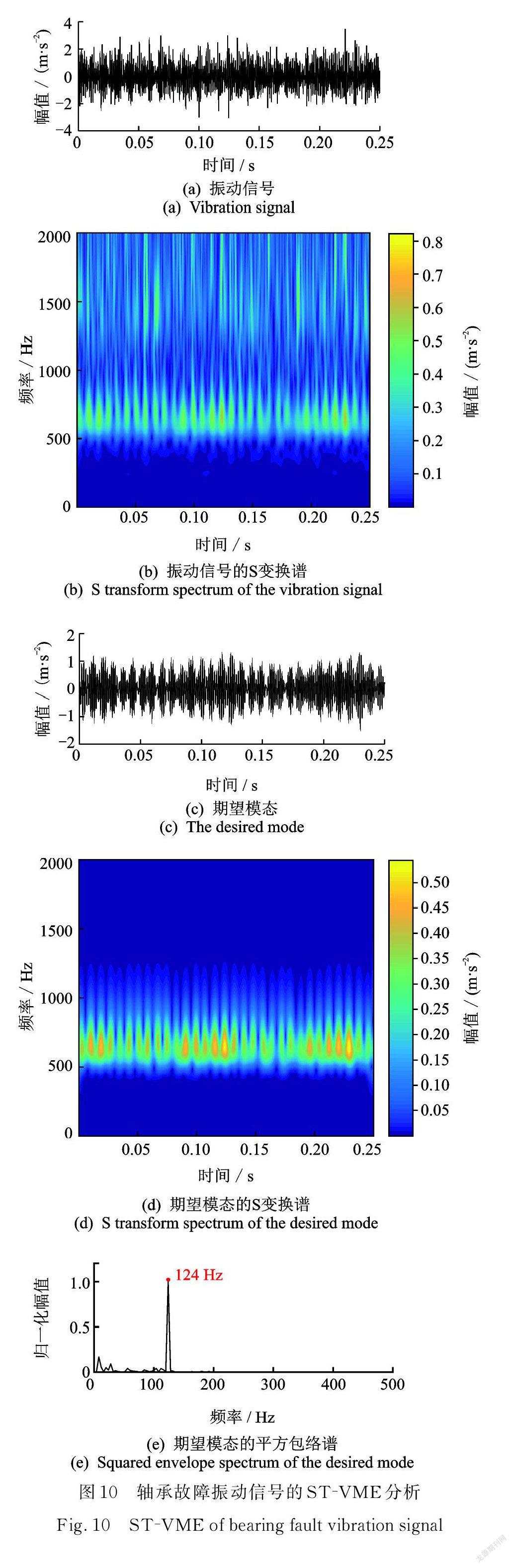
所用的轴承振动数据来源于 Case Western Re ⁃ serve University 电气工程实验室的轴承数据库。研究对象选为试验台驱动端的 NTN 滚动轴承，其内滚道上加工有一直径为0.7112 mm（0.028"），深度为1.27 mm（0.050"）的凹坑，用于模拟轴承的局部损伤故障。选用振动数据的试验台运行工况为：驱动电机功率2.2 kW，转速1730 r/min，加载电机载荷3 N ·m。经过分析该轴承内圈的故障特征频率fBPFI为124 Hz 。振动数据采样频率为12 kHz，得到一段数据长度为3000的振动信号，如图10（ a ）所示。该振动信号的 S 变换谱如图10（b）所示，可以看到大致在频段500～800 Hz 内，沿时间轴方向出现冲击特征，从中选取2π×650 rad/s 作为中心频率初始值，VME 提取出的期望模态如图10（ c ）所示，其 S 变换谱如图10（d）所示，可见其中显著的周期性冲击特征。期望模态的平方包络谱如图10（ e ）所示，提取出的轴承故障特征频率为124 Hz，与实际值一致。

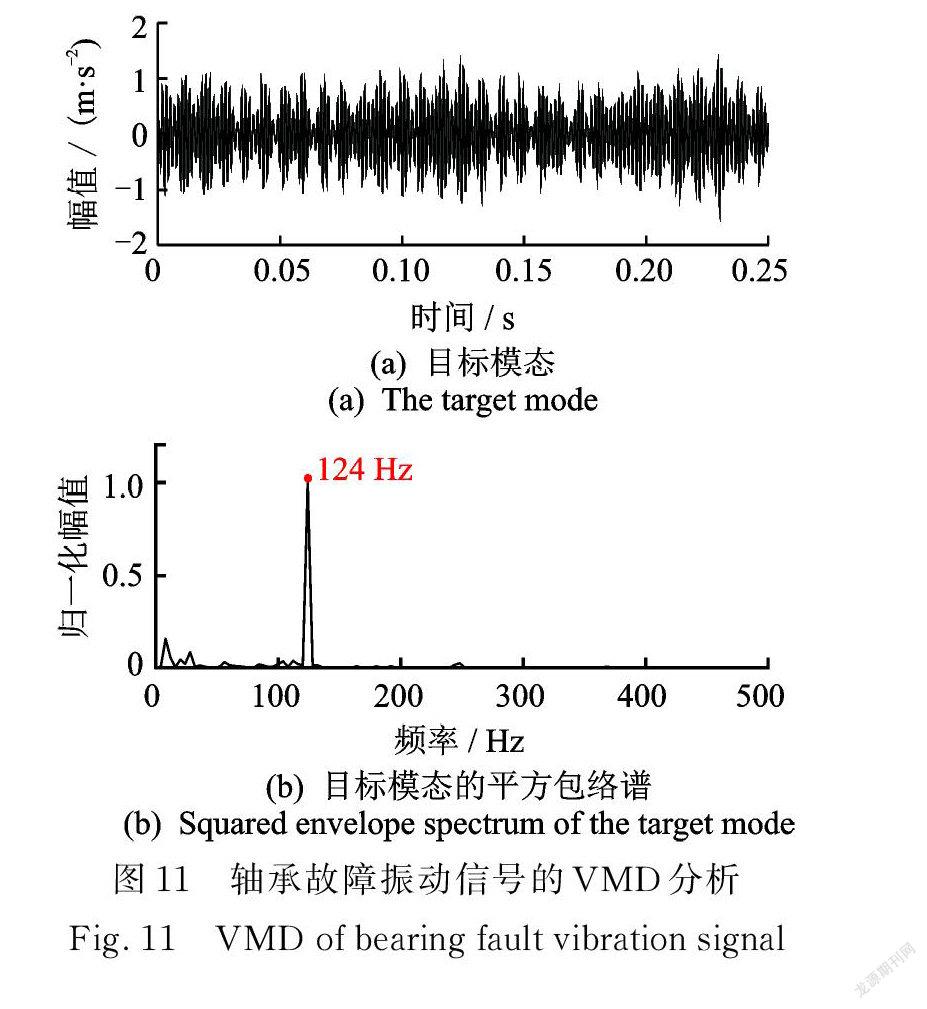
继续采用 VMD 对该组轴承振动信号进行处理，其中模态分解的层数设为5，分解结果中包含故障特征的目标模态为第1模态，如图11（ a ）所示，平方包络谱如图11（b）所示。通过对比可以看出， VME 获取的期望模态与 VMD 提取的目标模态对于轴承故障特征频率的提取效果基本相同，不过 VMD 方法在执行过程中，确定合适的模态分解层数和选取有用的目标模态，均带有一定的尝试性，这在一定程度上影响了 VMD 的使用效率。

4 结论

（1）VME 方法将信号分解成期望模态和残余信号两层，避免了 VMD 方法分解层数难以确定、目标模态难以选取的问题，具有更强的目标性，实施更容易。

（2）S 变换能够有效展示旋转机械振动信号中故障冲击特征所在的频段，成功用于 VME 期望模态中心频率初始值的选取，据此获取的期望模态包含了清晰完整的故障特征，并减少了噪声干扰，效果不亚于甚至优于 VMD 提取的目标模态。

（3）仿真信号与实际振动信号的分析结果表明，本文所提出的 ST⁃VME 故障诊断方法能够有效提取出齿轮或轴承的故障特征频率，实现旋转机械的故障诊断，具有广阔的应用前景。

参考文献：

[1] 李康强，冯志鹏.基于 EMD 和能量算子的模态参数识别在行星齿轮箱中的应用[ J ].振动与冲击，2018，37（8）：1-8.

Li Kangqiang，Feng Zhipeng . Modal parameter identifi⁃ cation based on empirical mode decomposition and ener⁃ gy operator for planetary gearboxes [ J ]. Journal of Vi⁃ bration and Shock，2018，37（8）：1-8.

[2]  Ye X  R，Hu Y  F，Shen J X，et al . An  adaptiveopti⁃mized  TVF-EMD  based  on  a  sparsity-impact  measure Index  for  bearing  incipient  fault  diagnosis [ J ]. IEEE Transactions  on  Instrumentation  and  Measurement，2021，70：1-11.

[3] 李华，刘韬，伍星，等.EEMD 和优化的频带熵应用于轴承故障特征提取[ J ].振动工程学报，2020，33（2）：414-423.

Li  Hua ，Liu  Tao ，Wu  Xing ，et  al . EEMD  andopti⁃ mized frequency band entropy for fault feature extraction of bearings[ J ]. ，2020，33（2）：414-423.

[4] 程軍圣，罗颂荣，杨斌，等. LMD 能量矩和变量预测模型模式识别在轴承故障智能诊断中的应用[ J ].振动工程学报，2013，26（5）：751-757.

Cheng  Junsheng， Luo  Songrong， Yang  Bin ， et  al . LMD  energy  moment  and  variable  predictive  model based  class  discriminate  and  their  application  in  intelli⁃ gent fault diagnosis of roller bearing [ J ]. Journal of Vi⁃ bration Engineering，2013，26（5）：751-757.

[5]  Zheng Z，Jiang W L，Wang Z W，et al . Gear fault diag⁃nosis  method  based  on  local  mean  decomposition  and generalized morphological fractal dimensions [ J ]. Mech ⁃ anism and Machine Theory，2015，91：151-167.

[6]  Liu Z，Zuo M J，Jin Y，et al . Improved local mean de⁃composition  for  modulation  information  mining  and  its application to machinery  fault diagnosis [ J ]. Journal of Sound and Vibration，2017，397：266-281.

[7]  Cao H R，Fan F，Zhou K，et al . Wheel-bearing fault di⁃agnosis of trains using empirical wavelet transform [ J ]. Measurement，2016，82：439-449.

[8]  Chegini  S  N ，Bagheri  A ，Najafi  F . Application  of  anew EWT-based denoising technique in bearing fault di⁃ agnosis [ J ]. Measurement，2019，144：275-297.

[9] 王奉涛，柳晨曦，张涛，等.基于 k 值优化 VMD 的滚动轴承故障诊断方法[ J ].振动、测试与诊断，2018，38（3）：540-547.

Wang Fengtao，Liu Chenxi，Zhang Tao，et al . Fault di⁃ agnosis  of rolling  bearing  based  on  k-Optimized  VMD [ J ]. Journal  of Vibration ，Measurement & Diagnosis，2018，38（3）：540-547.

[10]段晨東，张荣.基于改进经验小波变换的机车轴承故障诊断[ J ].中国机械工程，2019，30（6）：631-637.

Duan  Chendong， Zhang  Rong . Locomotive  bearing fault  diagnosis  using  an  improved  empirical  wavelet transform [ J ]. China Mechanical Engineering，2019，30（6）：631-637.

[11]乔志城，刘永强，廖英英.改进经验小波变换与最小熵解卷积在铁路轴承故障诊断中的应用[ J ].振动与冲击，2021，40（2）：81-90.

QiaoZhicheng，Liu Yongqiang，Liao Yingying . Loco ⁃ motive bearing fault diagnosis using an improved empiri⁃ cal  wavelet  transform [ J ]. Journal  of  Vibration  and Shock，2021，40（2）：81-90.

[12] Dragomiretskiy  K，Zosso  D . Variational mode decom ⁃position [ J ]. IEEE Transactions on Signal Processing，2014，62（3）：531-544.

[13]唐贵基，王晓龙.变分模态分解方法及其在滚动轴承早期故障诊断中的应用[ J ].振动工程学报，2016，29（4）：638-648.

Tang  Guiji，Wang Xiaolong . Variational mode decom ⁃ position method and its application on incipient fault di⁃ agnosis of rolling bearing [ J ]. Journal of Vibration Engi⁃ neering，2016，29（4）：638-648.

[14]徐元博，蔡宗琰，胡永彪，等.强噪声背景下频率加权能量算子和变分模态分解在轴承故障提取中的应用[ J ].振动工程学报，2018，31（3）：513-522.

Xu Yuanbo，Cai Zongyan，Hu Yongbiao，et al . A  fre ⁃ quency-weighted  energy  operator  and  variational  mode decomposition for bearing fault detection [ J ]. ，2018，31（3）：513-522.

[15] Li J M，Yao X F，Wang H，et al . Periodic impulses ex⁃traction  based  on  improved  adaptive  VMD  and  sparse code  shrinkage denoising  and  its  application  in rotating machinery fault diagnosis [ J ]. Mechanical Systems and Signal Processing，2019，126：568-589.

[16] Li H，Liu T，Wu X，et al . An optimized VMD methodand its applications in bearing fault diagnosis [ J ]. Mea ⁃surement，2020，166：1-8.

[17] Nazari M，Sakhaei S M . Variational mode extraction：anew  efficient method to derive respiratory  signals  from ECG [ J ]. IEEE Journal of Biomedical and Health Infor⁃ matics，2018，22（4）：1059-1067.

[18] Stockwell R  G，Mansinha L，Lowe R P . Localizationof the  complex  spectrum ：the  S  transform [ J ]. IEEETransactions on Signal Processing，2002，44（4）：998-1001.

[19]郭远晶，魏燕定，周晓军，等. S 变换时频谱 SVD 降噪的冲击特征提取方法[ J ].振动工程学报，2014，27（4）：621-628.

Guo Yuanjing，Wei Yanding，Zhou Xiaojun，et al . Im ⁃ pact  feature  extracting  method  based  on  S  transform time-frequency spectrum denoised by SVD [ J ]. ，2014，27（4）：621-628.

[20] Borghesani P，Pennacchi P，Chatterton S . The relation ⁃ship  between  kurtosis- and  envelope-based  indexes  for the diagnostic of rolling element bearings [ J ]. Mechani⁃cal  Systems  and  Signal  Processing ，2014，43（1-2）： 25-43.

Fault diagnosis method of rotating machinery using variational mode extraction guided by S transform

GUO Yuan-jing1，JIN Xiao-hang2，WEI Yan-ding3，YANG You-dong1

（1.Zhijiang College，Zhejiang University of Technology，Shaoxing 312030，China ；      2.College of Mechanical Engineering，Zhejiang University of Technology，Hangzhou 310023，China；3.Key Laboratory of Advanced Manufacturing Technology of Zhejiang Province，College of Mechanical Engineering， Zhejiang University，Hangzhou 310027，China）

Abstract： In order to solve the problems existing in variational mode decomposition（VMD） that the number of mode decomposi? tion layers is difficult to determine and the target mode is difficult to select，an improved signal decomposition method，i . e .，varia⁃ tional mode extraction （VME） is introduced . And a fault diagnosis method of rotating machinery based on S transform （ST） and VME is proposed . Based on a new criterion that the spectrum overlap between the desired mode and the residual signal is mini⁃ mized，VME method decomposes the signal into two layers，i . e .，the desired mode and the residual signal . Aiming to obtain the desired mode containing abundant fault features，the signal is processed by S transform to determine the frequency band of the fault features . Consequently，the central frequency initial value of the desired mode of VME is obtained . In order to extract the fault char⁃ acteristic frequency from the desired mode，the squared envelope spectrum （SES） analysis method is applied to process the desired mode . The analysis results of the simulated signal and actual vibration signals show that the proposed ST -VME method can suc ⁃ cessfully extract the valuable desired mode and the accurate fault characteristic frequency to achieve rotating machinery fault diagno ⁃ sis . Besides，compared with VMD，the ST-VME method is more targeted and easier to implement .

Key words ： fault diagnosis；rotating machinery；variational mode extraction；S transform；squared envelope spectrum

作者简介：郭远晶（1987—），男，博士，讲师。电话：（0575）81112562；E-mail：gyjyn@126.com。

通讯作者：杨友东（1970—），男，博士，教授。电话：（0575）81112537；E-mail：yydong@zjut .edu .en。