含行星轮局部故障的行星齿轮箱振动仿真及实验研究

樊家伟 郭瑜 伍星 林云 陈鑫

摘要：针对现有行星齿轮箱局部故障振动仿真模型使用小波变换和加窗振动分离技术进行故障诊断时效果不明显的问题，提出了一种以齿轮啮合冲击响应和齿轮啮合顺序为基础的行星轮局部故障振动仿真模型。以齿轮啮合冲击响应为基础，仿真正常齿和故障齿的单次啮合冲击振动响应；计算每次齿轮啮合的时间点，按照轮齿啮合顺序使用单次啮合冲击振动响应进行拼接，综合考虑振动信号的时变传递路径和太阳轮、行星轮和行星架转频的调制影响；建立了满足加窗振动分离技术故障特征提取的行星轮局部故障振动仿真模型。通过与行星齿轮箱的试验平台实测振动信号和振动仿真信号的分析对比，验证了所建立模型的正确性。

关键词：故障诊断；行星齿轮箱；振动信号仿真；加窗振动分离技术

中图分类号： TH165+.3；TH132.4    文献标志码： A    文章编号：1004-4523（2022）05-1270-08

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.025

引言

在故障诊断领域，合理的仿真信号对新技术和方法的验证有重要意义[1]。行星齿轮箱是故障诊断领域的重要研究对象，其通常包含多个行星轮，每个行星轮都同时与齿圈和太阳轮啮合，因此多个啮合点同时存在，且啮合位置随着时间不断变换。当采用固定位置安装传感器拾取其振动信号时，行星轮和啮合点位置的时变会导致啮合点与传感器之间的传递路径也存在时变性，因此，行星齿轮箱局部故障信号的仿真较为复杂[2]。

基于现象的振动信号仿真模型最早由 Randall[3]提出，使用预期频谱实现对故障齿轮振动的仿真。在行星齿轮箱振动仿真方面，近年来一些学者先后通过分析行星齿轮箱运转中各部件的频率，使用频谱成分实现了行星齿轮箱振动的仿真[4⁃6]，这些研究成果对行星齿轮箱故障诊断方法的研究提供了重要的评价依据。

另一方面，加窗振动分离技术是消除行星齿轮箱振动时变传递路径的有效方法[7⁃9]，可实现对行星轮或太阳轮故障的有效检测；小波变换也是实现齿轮故障诊断的一种常用方法[10⁃11]。然而现有的现象模型中正常齿和故障齿冲击均采用正弦调制产生，使用加窗振动分离技术时，截取到的信号是正弦调制的一部分，

其幅值变化较缓，无法观察到故障冲击特征，使用小波变换也无明显效果。本文在现有模型的基础上，针对该问题提出一种以齿轮啮合冲击响应和齿轮啮合顺序为基础的行星轮局部故障振动仿真模型。

研究中通过对行星齿轮箱振动机理进行分析，以齿轮啮合冲击响应为基础，综合考虑振动信号的时变传递路径和太阳轮、行星轮及行星架转速调制的影响，建立了基于齿轮啮合冲击响应的行星轮局部故障振动仿真模型。通过与实测振动信号的加窗振动分离结果对比分析，验证了所建立模型的正确性。

1 齿轮的啮合冲击响应

齿轮的啮合过程发生在单齿啮合与双齿啮合的瞬间，每次啮合会产生一次冲击响应，引起冲击响应的原因不仅有啮合力的影响，还有啮合刚度的影响[12]。

齿轮传动过程中，轮齿啮合刚度是随啮合点位置的变化而变化的，也即是时间 t 的函数。设啮合刚度 K（t）在单齿啮合区内为 K1，在双齿啮合区内为 K2，则 K（t）可展开为如下所示的傅里叶级数形式[12]：

式中  F 为冲量，是啮合冲击力在单次冲击时间内的积分；ζ为阻尼系数；me1，me2分别为主、被动齿轮的当量质量。研究中，F 设为0.139 N·s；ζ为-0.08； me1，me2分别为2和0.5；固有频率约为1400 Hz。

由式（3）可知，啮合刚度变化会影响齿轮的啮合冲击响应。由于局部故障会使齿轮的啮合刚度减小，导致啮合冲击响应幅值增加，可用其仿真行星轮局部故障对应的冲击响应。

2 故障行星轮振动信号仿真模型

2.1 正常状态下行星齿轮箱振动信号仿真模型

本文以由三个行星轮、一个太阳轮和一个齿圈组成的行星齿轮箱为例，其存在内齿圈与行星轮啮合、太阳轮与行星轮啮合共6个啮合点。实际振动拾取中振动传感器一般固定安装在箱体上。由于传感器安装位置正下方拾取到的啮合振动信号最强，为简化模型，在故障行星轮振动信号模型建立过程中，仅考虑传感器正下方区域的行星轮与齿圈啮合点的振动信号[5]。理想情况下，正常状态每个行星轮与齿圈啮合产生振动冲击响应均相同。

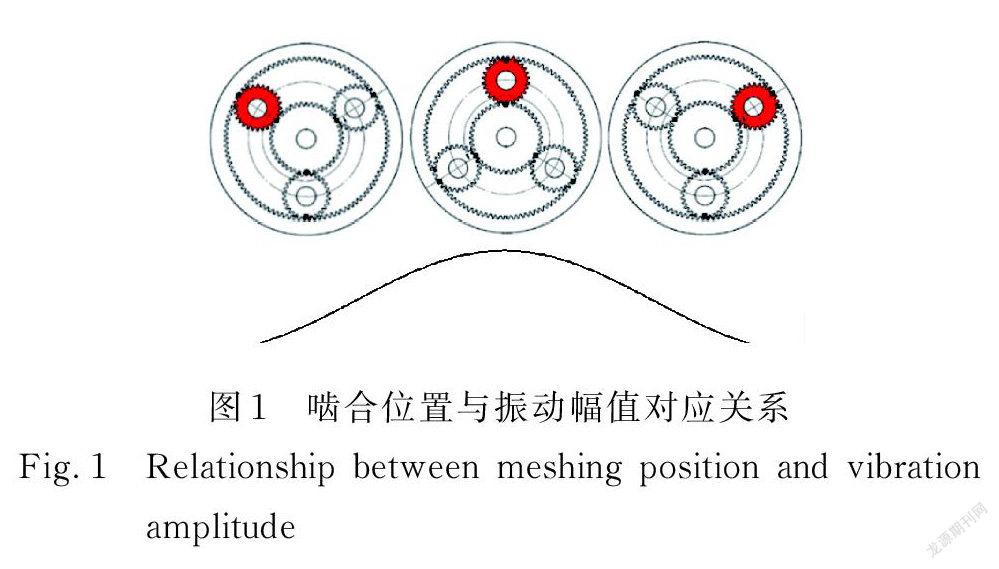
由于行星轮绕行星架中心轴的公转，行星轮在轮系中的位置发生周期性的变化，并导致啮合点与传感器之间的振动传递路径发生变化。如图1所示，当轮系顺时针旋转时，红色行星轮由远及近靠近传感器安装位置、再由近及远远离传感器安装位置，传感器拾取到的振动信号幅值变化为由小到大再从大到小，该时变传递路径引起的幅值变化可以用汉宁窗表示[6，14]。

行星架每旋轉一周，三个行星轮分别通过传感器正下方区域一次，行星轮与齿圈啮合的时变传递路径效应可表示为[6]：

式中 A 为传递函数幅值系数，传递路径最远点幅值为最近点的（A -1） A 倍，N 为行星轮个数，fc 为行星架旋转频率。

依据行星齿轮传动原理，对于行星轮，当行星架转过一定的圈数，行星轮轮齿与齿圈上特定齿（如传感器正下方的轮齿）的啮合会重复出现，定义重复啮合的最小圈数为NReset [15]：

式中 LCM 为求最小公倍数操作，Zr 为齿圈齿数，Zp为行星轮齿数。行星轮整周期啮合次数Nend可表示为：

单齿啮合时间：

式中fm为啮合频率，其倒数为单次啮合时间。根据式（3），计算第 n 个Δt 内的啮合冲击响应rnΔt，按照整周期内的啮合顺序将正常齿单次啮合冲击响应拼接起来，得到未经时变传递路径函数与转速调制的整周期的仿真信号，可表示为：

由式（8）综合考虑时变传递路径、太阳轮、行星轮与行星架转频引起的调制影响，可得到如下正常状态行星齿轮箱振动信号仿真模型：

式中  As，Ap 和 Ac 为太阳轮、行星轮和行星架的调幅系数；φs，φp 和φc 为太阳轮、行星轮和行星架的初始相位；fs，fp和fc 为太阳轮、行星轮和行星架的的转频。研究中，As，Ap 和 Ac 分别设置为0.3，0.2和0.5；φs，φp 和φc 分别设置为π/7，π/5和π/3，通过齿数计算得到太阳轮、行星轮和行星架的转频数值。

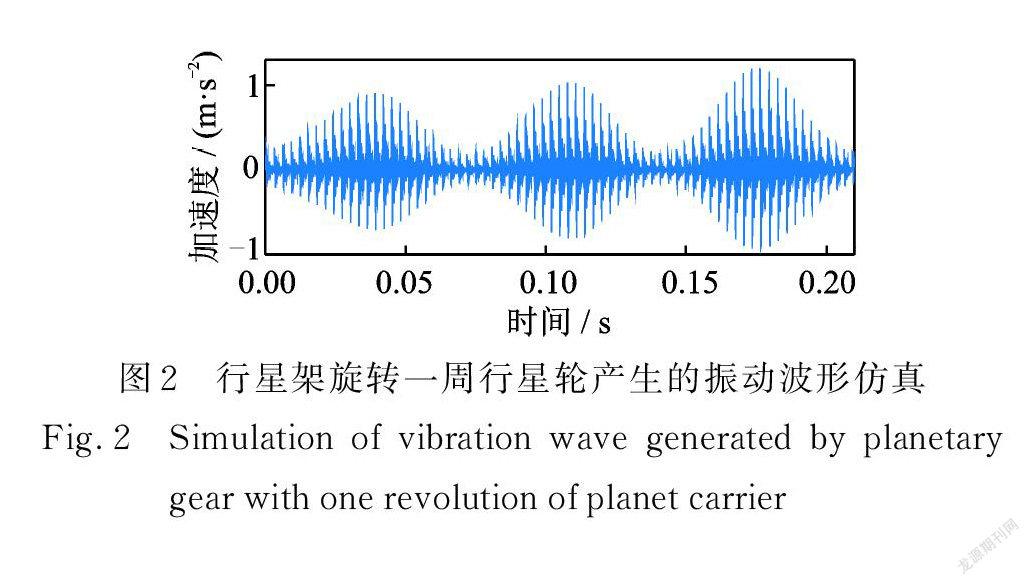
图 2 为行星架旋转一圈时正常状态下传感器拾取的振动仿真信号，反映了 3 个行星轮依次通过传感器正下方前后，由于行星轮时变传递路径的影响产生的3个幅值调制包络。

2.2 故障行星轮振动信号仿真模型

当某个行星轮发生局部故障，其故障轮齿与齿圈的啮合刚度 K（t）发生变化，由式（3）可知其啮合产生的冲击响应也将发生变化。减小式（3）中啮合刚度的数值，其他参数保持不变，即可得到单次啮合时间Δt 内故障齿啮合冲击响应 RΔt 。当故障行星轮所有轮齿与齿圈啮合一次出现一次故障啮合冲击响应，即每Zp次啮合中有一次故障冲击。将式（8）中特定啮合位置的信号替换为故障冲击响应信号，即可得到如下未经时变传递路径函数与转速调制的故障行星轮振动信号仿真模型：

式中Zp为行星轮齿数，Nend为完成一次行星轮整周期所需的啮合次数。

根据行星轮的时变传递路径，当故障轮齿与齿圈啮合点处于传感器正下方区域的齿圈部分时，传感器才能拾取到最强故障冲击响应信号。与正常状态下振动仿真信号相同，考虑时变传递路径、转频对 R（t）的调制可得如下故障行星轮振动信号仿真模型：

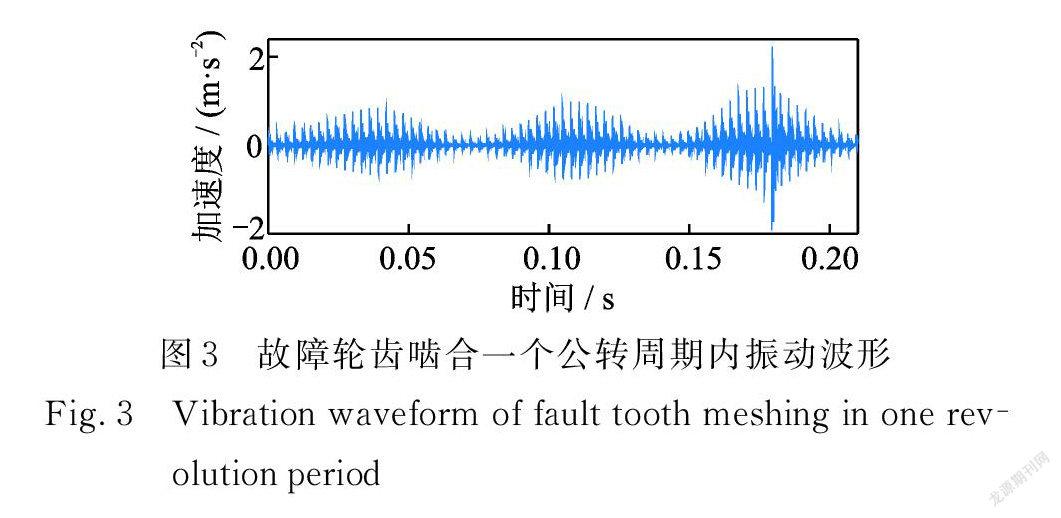
故障行星轮振动信号模型的时域波形如图3所示。与正常状态类似，行星架旋转一周也存在3个等间距的包络，但由于故障齿的存在，每进行一次啮合，传感器会拾取到一次故障齿与齿圈轮齿啮合引起的故障冲击。由于故障齿的刚度减小，其啮合较正常齿啮合产生一个幅值较大的冲击。

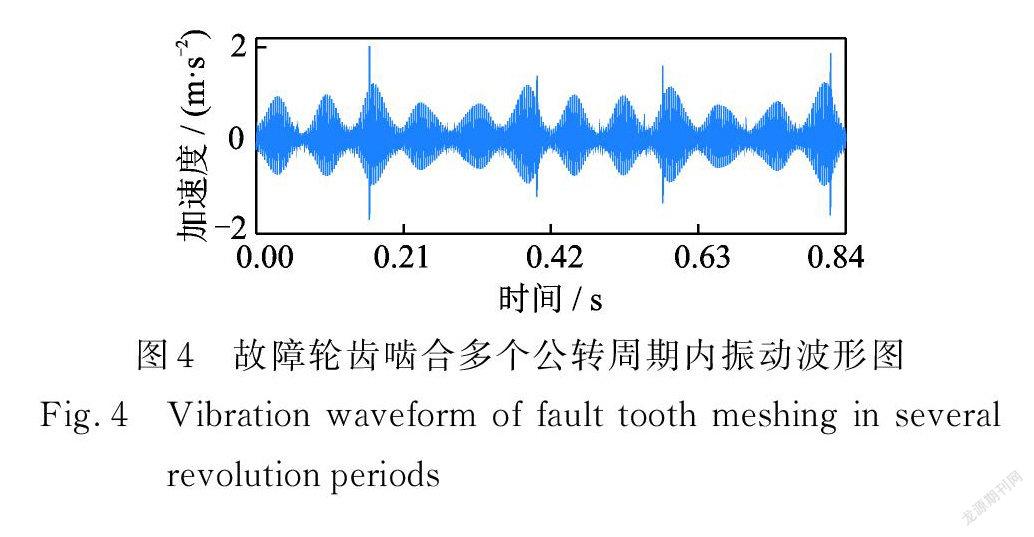
图4为行星架旋转多次的振动仿真信号，可以看出，行星架每旋转一周产生的3个幅值包络中，存在一个突出的故障冲击响应。值得注意的是，由于时变传递路径的影响，每次故障冲击出现的位置和幅值因为啮合位置的变化各不相同。

3 实验验证

3.1 实验简介

为验证本文所建立模型的正确性，使用行星齿轮箱试验平台获取实测振动信号，与仿真模型进行对比分析验证。实验研究对象为如图5为所示75 kW 传动实验台上的 NGW 行星齿轮箱（如图6所示）。

使用3个 DH112压电式加速度传感器及配套电荷放大器拾取行星齿轮箱输入轴（图6位置1）、齿圈（图6位置2）和输出轴（图6位置3）处振动信号，采用电涡流位移传感器（图6位置4）获取转速脉冲信号。

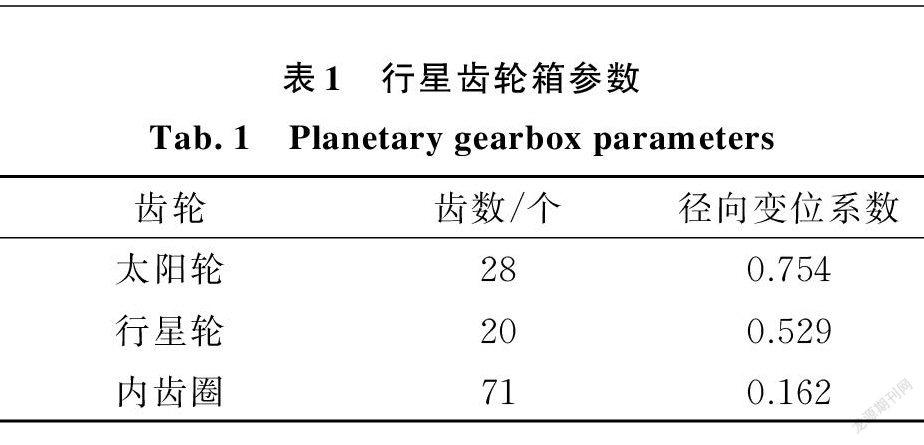
NGW 行星齿轮箱参数如表1所示。

为模拟行星轮局部故障，在一个行星轮上采用电火花加工一个齿根裂纹故障，行星轮系结构及人造齿根裂纹故障行星轮如图7所示。

实验时转速设置为1000 r/min，采样时长为180s，采样频率采用51.2 kHz 。研究中，安装在齿圈上方（图6位置2）的传感器获得的振动信号传递路径最短[5]、信号衰减较少，故使用该处振动信号进行验证。

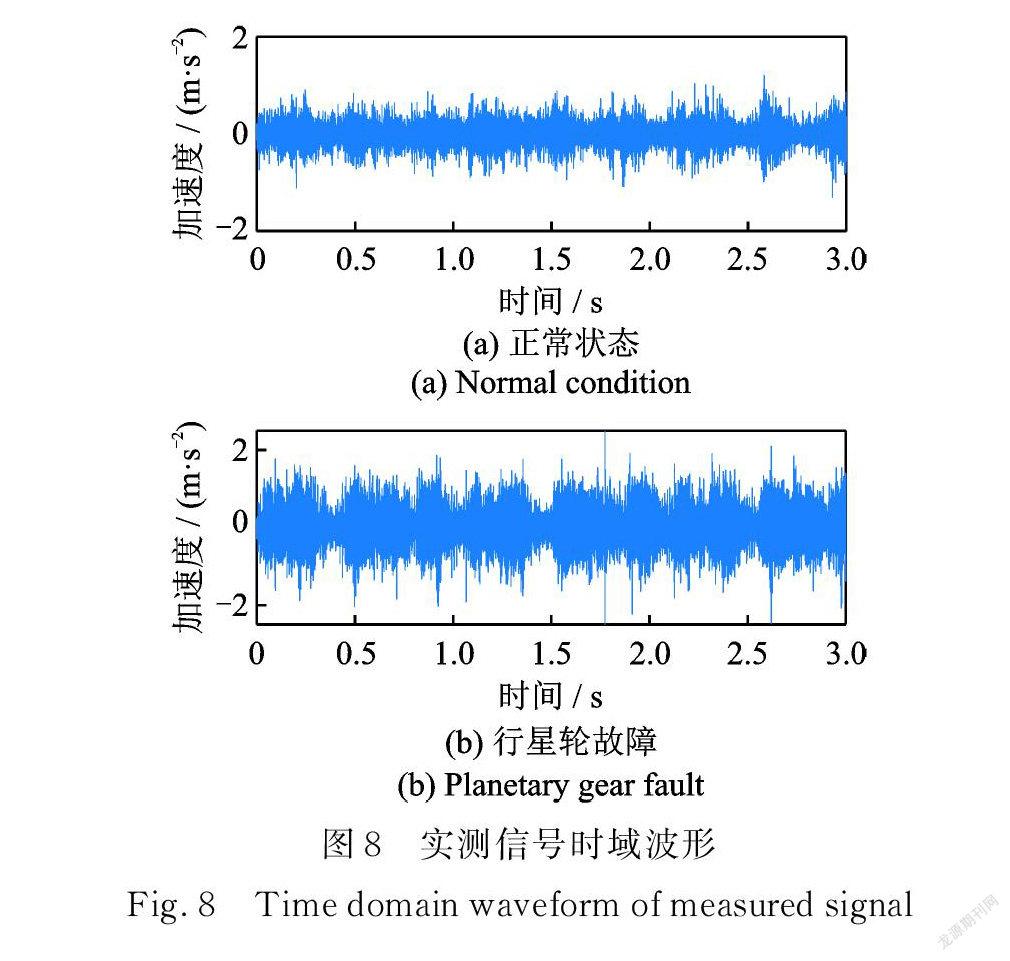
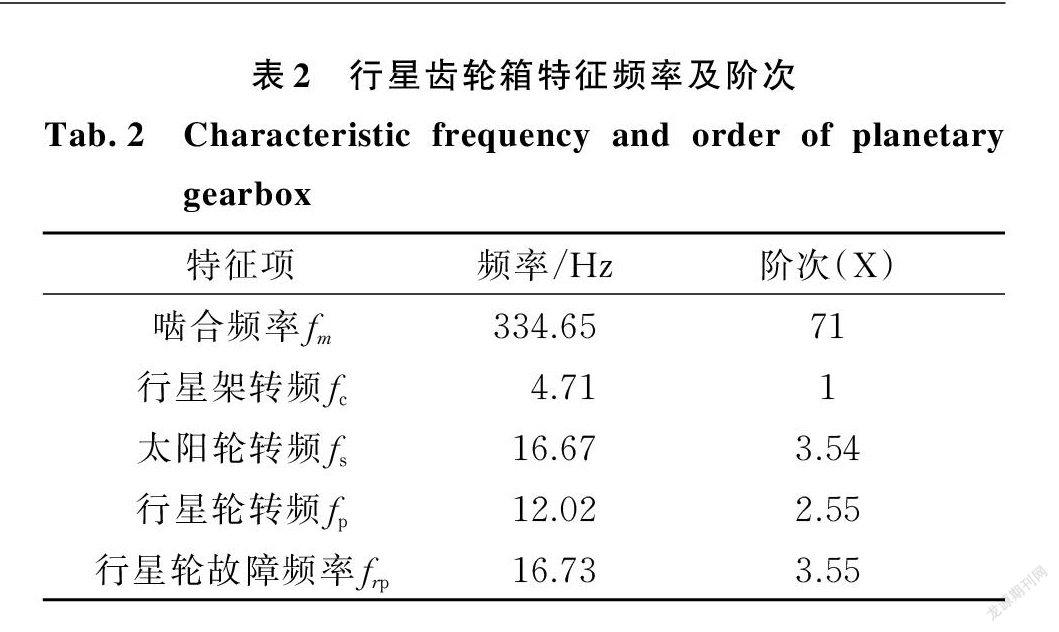
试验中，拾取到的正常状态和行星轮故障状态的振动信号波形如图8所示。由转速1000 r/min 及表1中参数可计算出行星齿轮箱的特征频率及以行星架为参考的特征阶次，如表2所示。

3.2  正常状态下振动仿真信号与实测信号对比分析

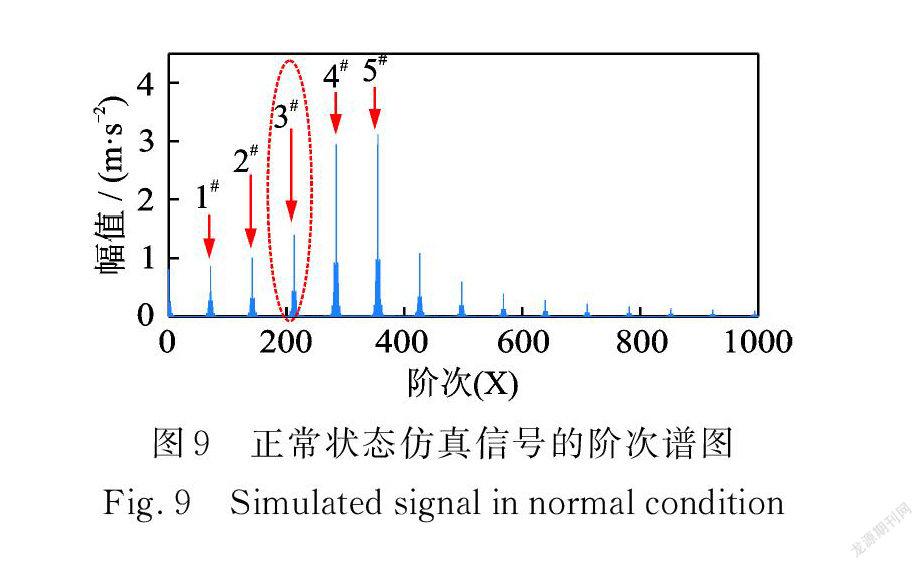
正常状态下振动仿真信号的阶次谱（以行星架转频为参考）如图9所示，图中以1#，2#和3#等分别表示啮合频率fm对应的啮合阶次以及各阶倍频。

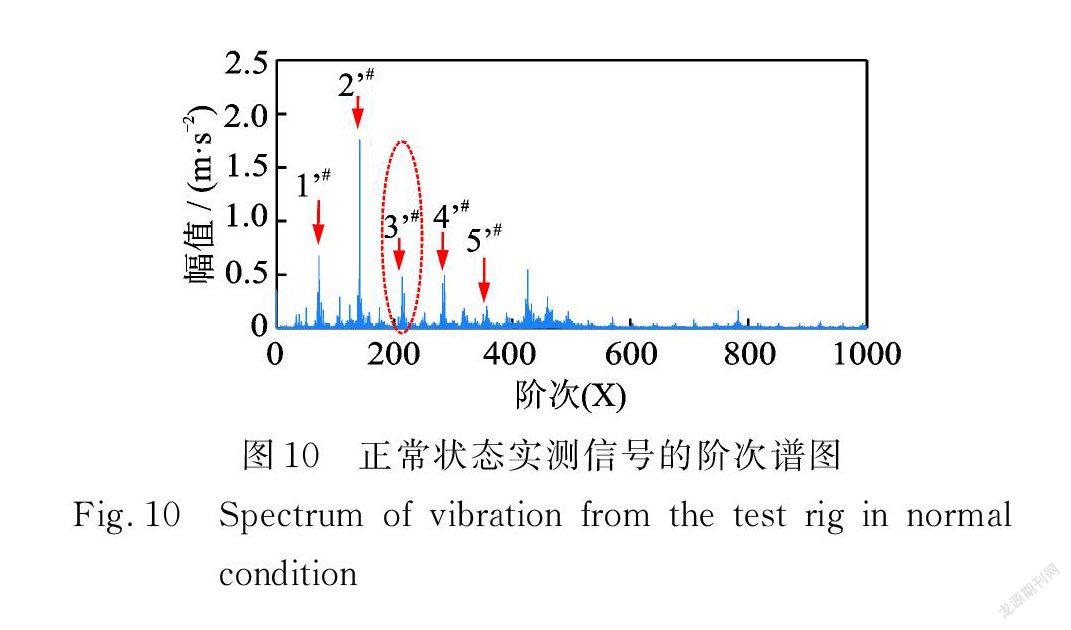
实测正常状态信号阶次谱图如图10所示，可以看出其阶次谱中同样存在啮合频率fm对应的啮合阶次以及啮合阶次的倍频，如1’#，2’#和3’#等。

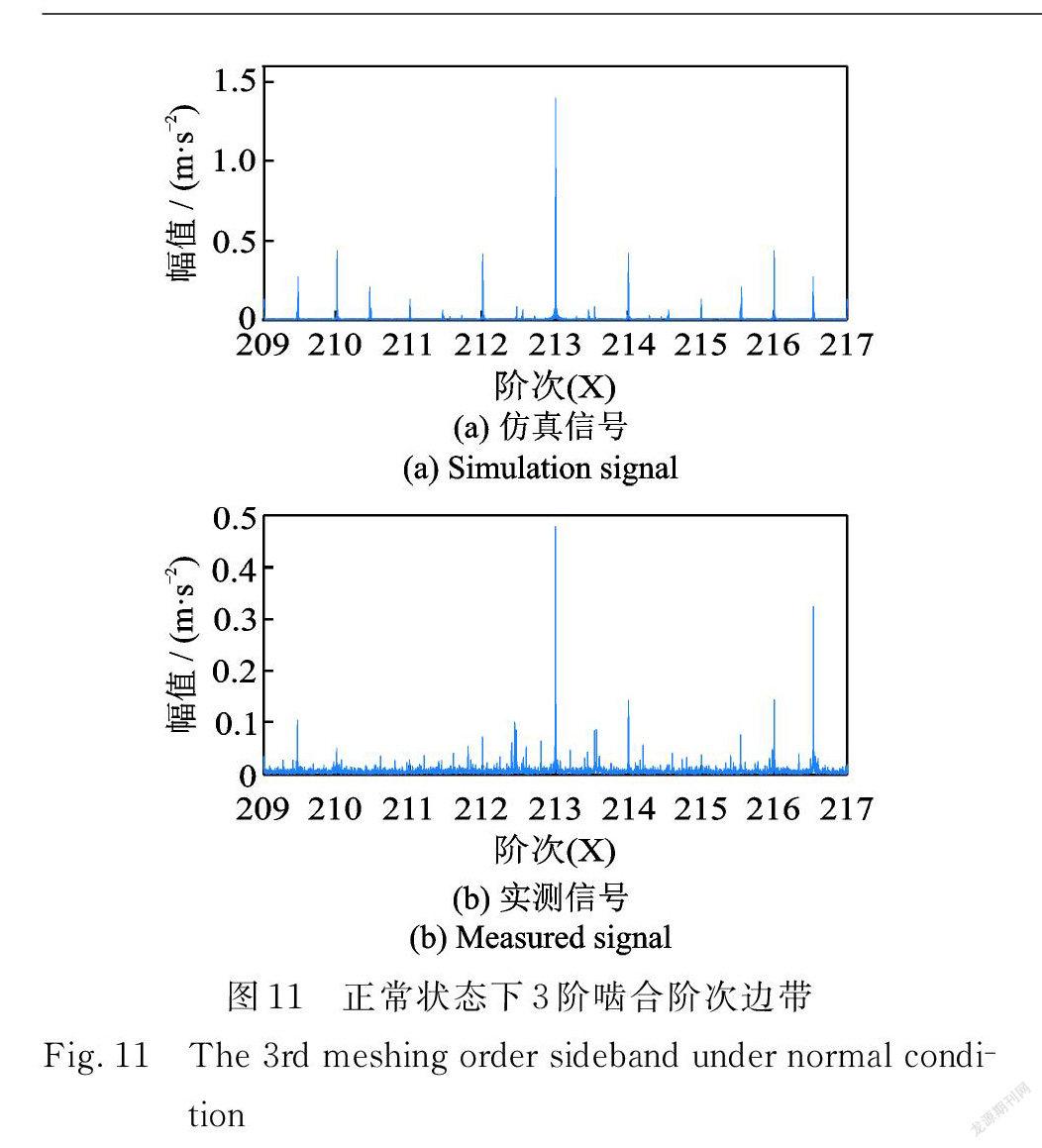
由于实测故障信号啮合频率倍频3fm 对应阶次处的边带成分较丰富，且比其他谐波的边带更清晰。为方便对比，研究中所有信号均采用3fm 处的边带进行局部放大。正常状态下仿真信号与实测信号3阶啮合阶次及其边带如图11所示。可以看出虽然实测信号3阶啮合阶次的边带存在一定的干扰，但其频率规律基本与仿真信号边带吻合。

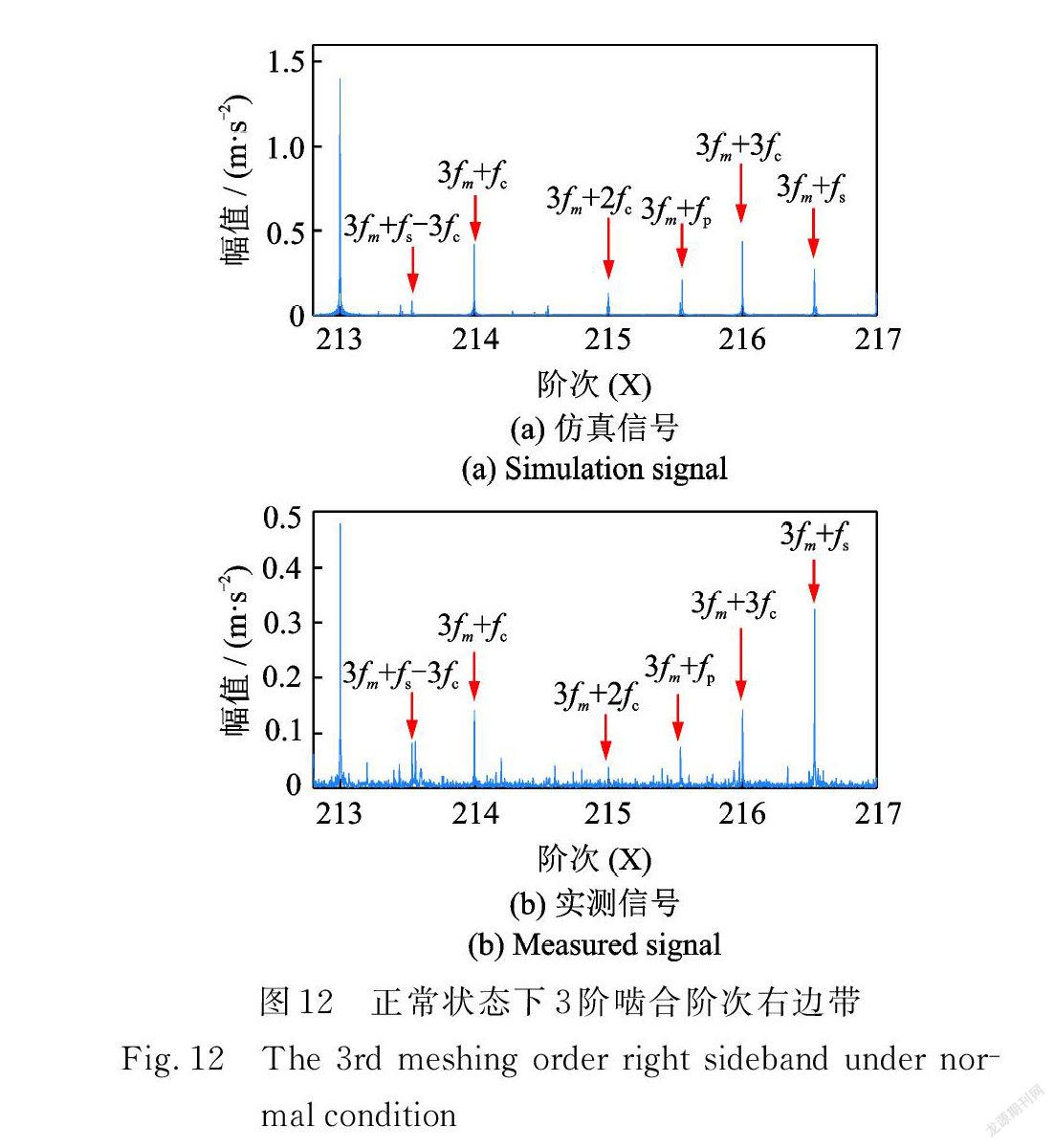
对比正常状态下仿真信号与实测信号3阶啮合阶次边带，为显示其细节，取其右边边带进行分析，如图12所示。仿真信号3阶啮合频率对应阶次的右边带如图12（ a ）依次为：3fm +fs -3fc，3fm +fc，3fm +2fc，3fm +fp，3fm +3fc 和3fm +fs 。实测信号3阶啮合阶次的右边带如图12（b）所示，与仿真信号依次对应，其中3fc 为行星轮时变传遞路径函数出现的频率Nfc （N=3）。边带3fm +fs -3fc 是太阳轮转频和行星轮与齿圈啮合的时变传递路径效应频率的差值调制造成；3fm +fc，3fm +2fc 和3fm +3fc 是由于行星架转频的调制产生；3fm +fp由行星轮转频调制产生；3fm +fs 由太阳轮转频引起。

由于行星齿轮箱的试验传动台包含其他齿轮箱及电机等，并且行星齿轮箱不可避免地存在制造、安装误差，致使传感器拾取到的信号中存在大量系统产生的干扰信号；同时，齿轮箱中包含齿轮、轴、轴承及箱体等零部件，其固有频率各不相同，造成振动信号中共振现象复杂。因此，实测信号与仿真信号阶次谱存在一定差异，但总体上两者的阶次谱基本一致，验证了正常状态下振动信号仿真模型的正确性。

3.3  故障行星轮振动仿真信号与实测信号对比分析

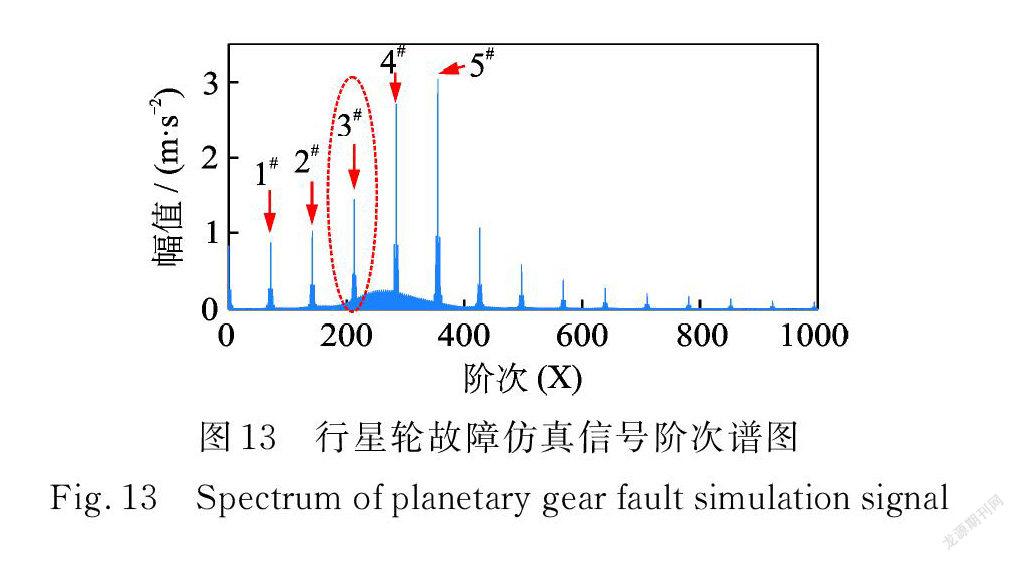
故障行星轮振动仿真信号的阶次谱如图13所示，啮合频率fm对应的啮合阶次以及倍频同样存在。

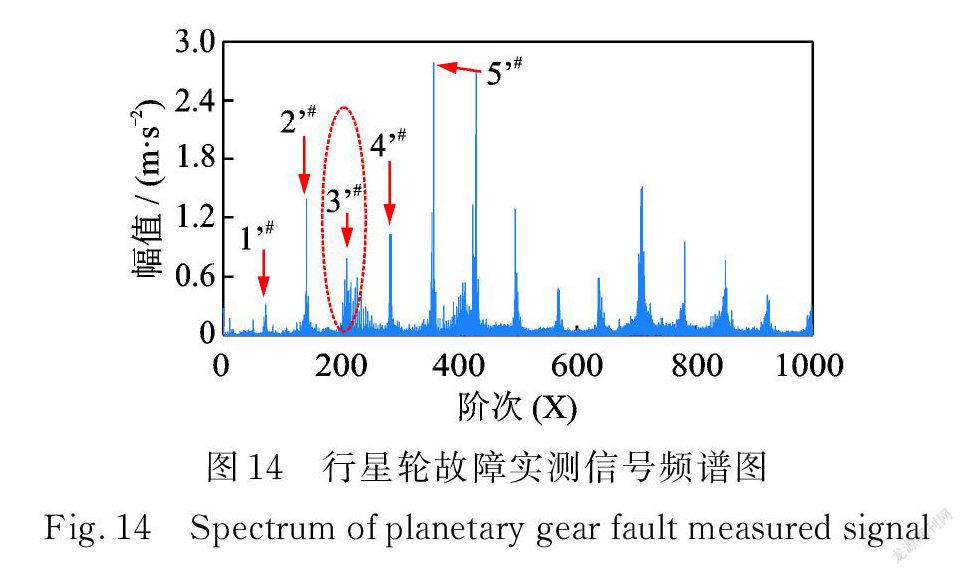
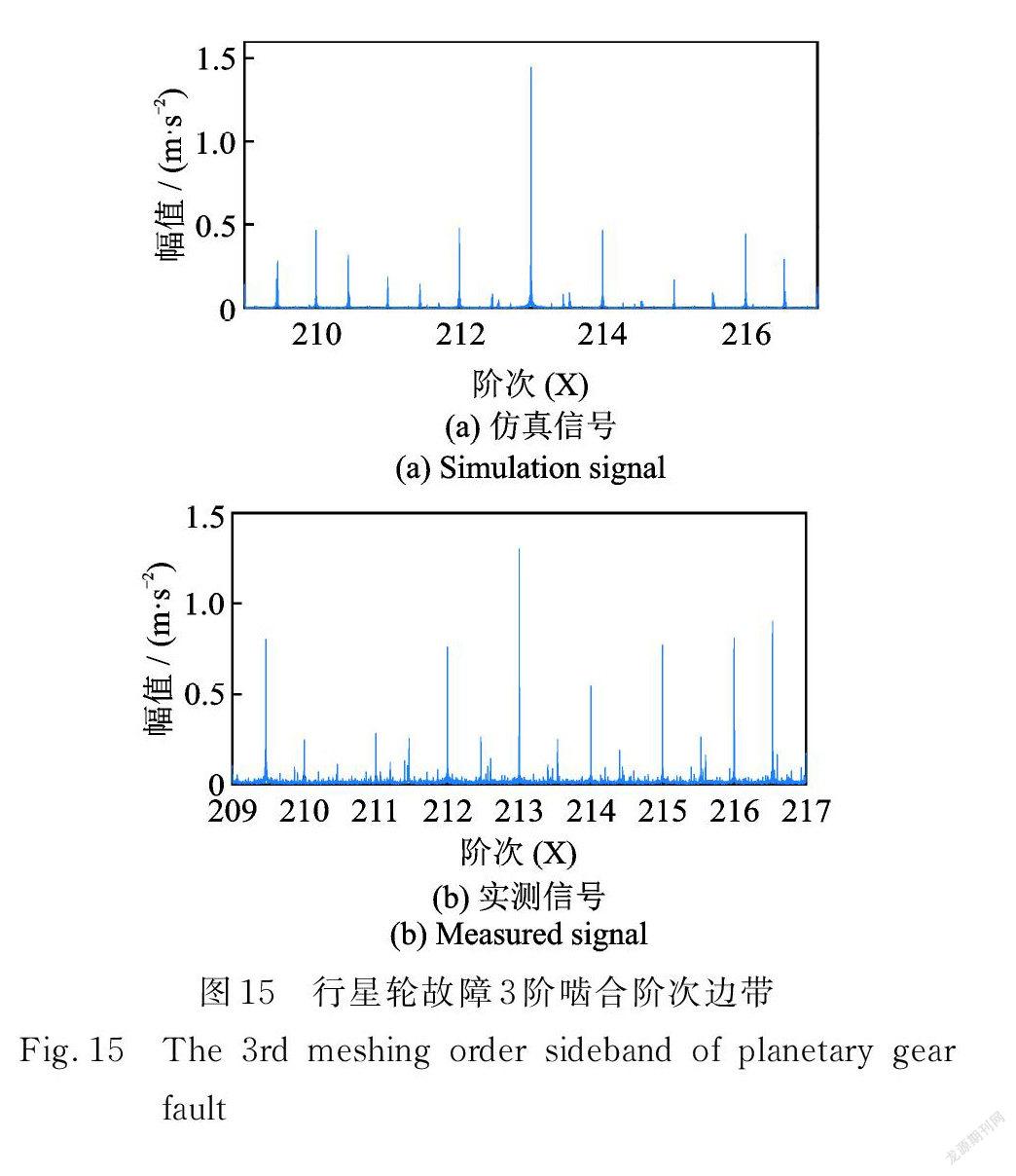
实测行星轮故障振动信号阶次谱图如图14所示，与仿真信号阶次谱相比，两者虽存在一定差异，但总体上实测信号阶次谱与仿真信号阶次谱基本一致。仿真与实测信号3阶啮合阶次及其边带如图15所示，可以看出幅值由于干扰的影响存在一定差异，但两种边带总体吻合。

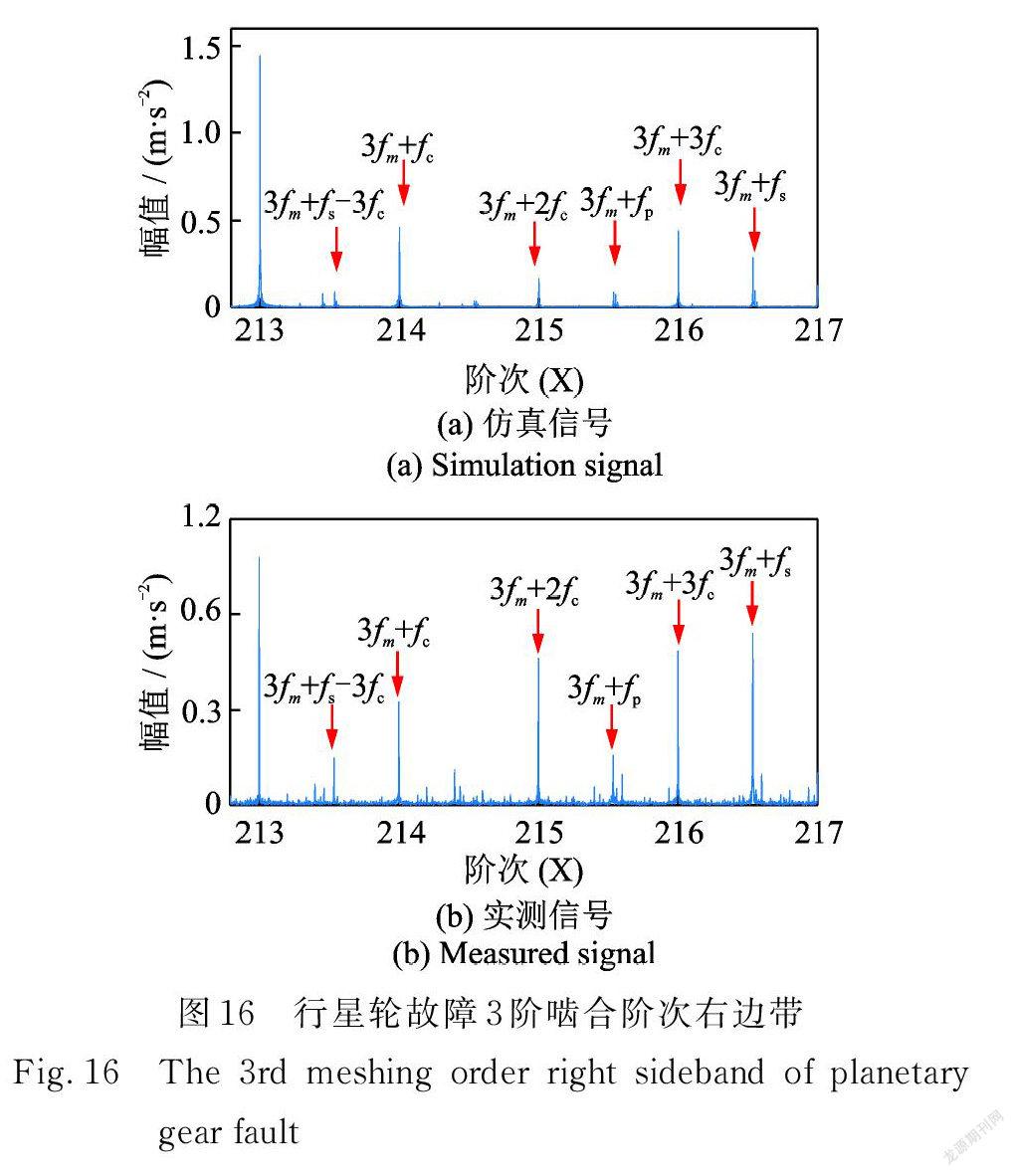
行星轮故障仿真信号与实测信号3阶啮合阶次边带进行对比（只显示右边单边），如图16所示。仿真信号3阶啮合阶次的边带如图16（ a）依次为：3fm +fs -3fc，3fm +fc，3fm +2fc，3fm +fp，3fm +3fc 和3fm +fs 。实测信号3阶啮合阶次的右边带如图16（b）所示，与仿真信号一一对应，边带谱线的形成原因与正常状态下一致。

由于行星齿轮箱振动信号受时变传递路径影响，且试验台干扰源较多，试验用齿轮箱的太阳轮转频fs 阶次为3.53X、行星轮故障特征频率frp阶次为3.55X，在阶次谱图中重叠为一条谱线，正常状态与行星轮故障的阶次谱边带相似，仅幅值有所差别，故仅凭啮合阶次及其倍频的边带判断故障较为困难。使用齿数比为齿圈77、太阳轮43、行星轮17的行星齿轮箱振动仿真信号进行分析对比，可以在啮合频率边带处观察到明显的故障特征谱线。

3.4 基于加窗振动分离技术的特征提取方法试验分析

加窗振动分离技术是可以有效消除时变传递路径影响的方法，其原理与实现具体详见文献[8⁃9，16]。如前言所述，现有行星齿轮箱振动仿真信号模型采用正弦谐波拟合行星轮系的啮合和故障冲击响应成分，导致现有仿真模型使用加窗分离和小波变换技术提取故障齿冲击失效，如文献[5]所提行星轮局部故障仿真模型：

式中fpf为行星轮局部故障特征频率；A，B 分别为故障调幅、调频系数；ϕ和φ为初始相位。

本文所提行星齿轮箱振动信号仿真模型按照实际齿轮啮合顺序拼接单齿啮合冲击响应仿真振动信号，使用加窗振动分离技术在时域波形中加窗截取时，可以截取到故障轮齿啮合的冲击响应，有效提取到故障冲击，使用小波变换也可以增强仿真信号中的冲击响应，加窗振动分离技术主要用于实验分析。研究中加窗振动分离截取的总周期（对应行星轮与特定齿啮合的最小圈数NReset ）为30，同步平均的长度为10个周期（对应行星轮），同步平均次数为20。对实测信号使用同样的参数做加窗振动分离[8，16]，并对其结果进行对比。

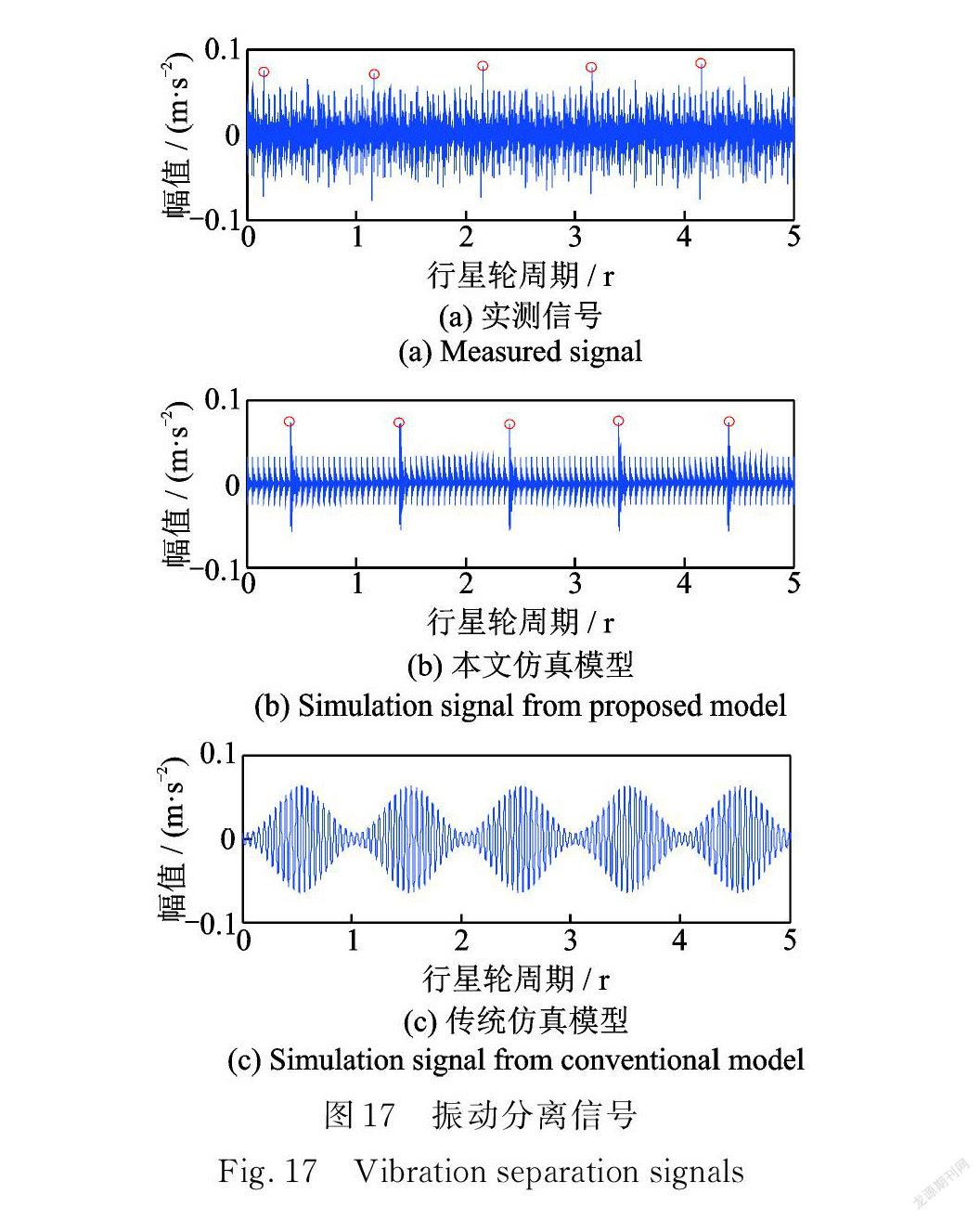
如图17（ a ）所示为实测故障行星轮振动信号使用加窗振动分离技术获取到的行星轮故障振动分离平均信号，可以在分离信号中观察到较明显的周期性故障冲击被有效提取；图17（b）为本文所提仿真模型使用加窗振动分离技术获得的振动分离信号，可以看出其中明显的周期故障冲击成分；图17（ c ）为文献[9]所提的行星轮局部故障振动仿真模型使用加窗振動分离技术获得的振动分离信号，其不含有周期性冲击成分，与图17（ a ）所示实测信号振动分离结果存在较大差别。

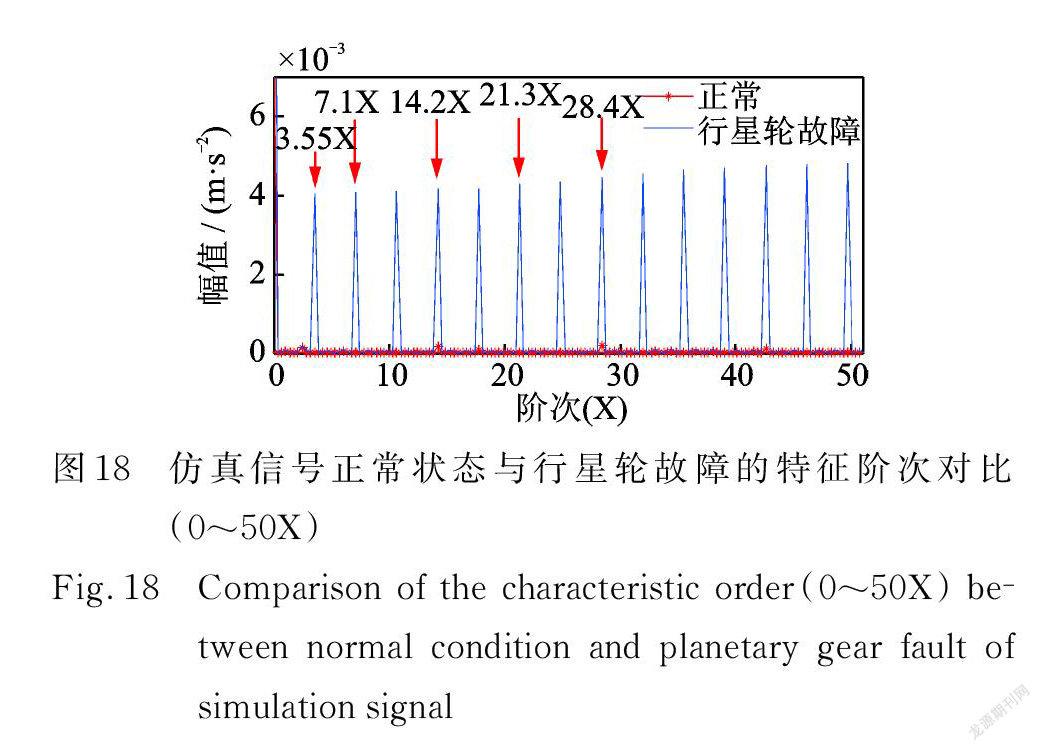
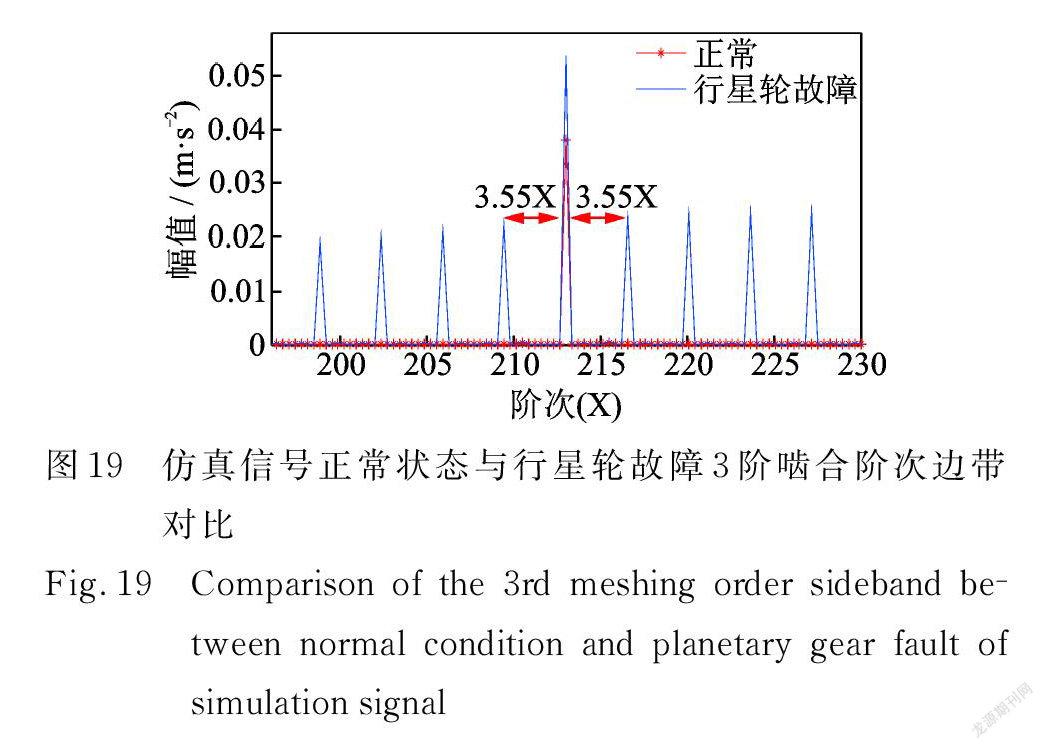
图18为正常状态和行星轮故障仿真信号的振动分离信号的前50X 阶次谱图，可以明显看出行星轮故障阶次3.55X 及其谐波谱线，而正常状态的阶次谱不能观察到明显的故障特征阶次，且幅值与行星轮故障状态差异较大；图19为其3阶啮合阶次（213X）的边带，可以明显看出行星轮故障状态下存在3.55X 及其谐波的边带，而正常状态无边带。

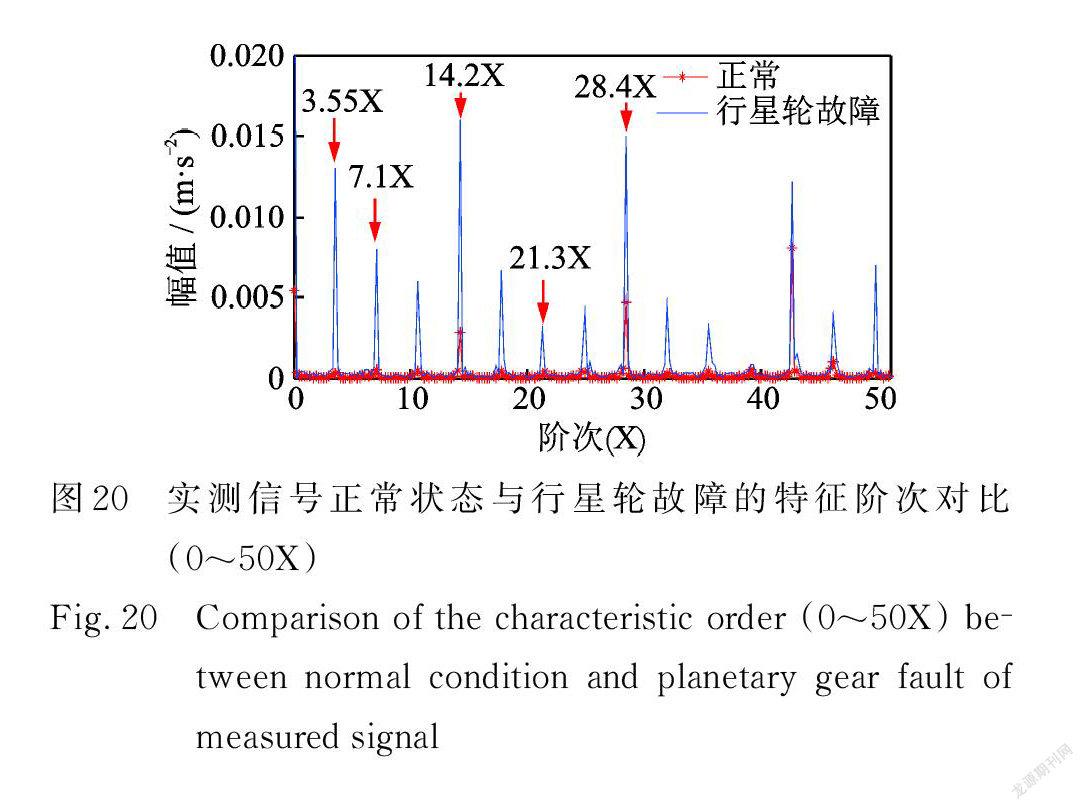
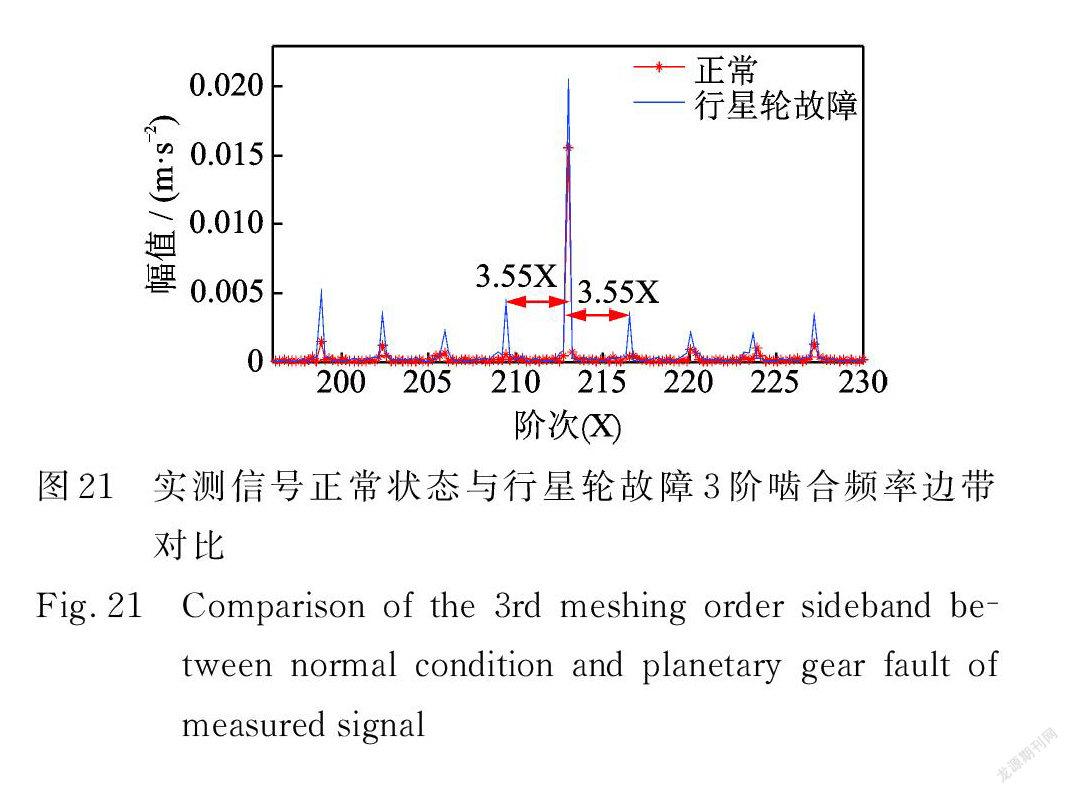
行星轮故障、正常状态实测信号的振动分离信号的前50X 阶次谱图如图20所示，从行星轮故障的阶次谱中可以明显观察到3.55X 阶及其谐波，而正常状态的阶次谱中该阶次频率不明显；图21为3阶啮合阶次（213X）的边带，可以明显看出行星轮故障状态下存在3.55X 及其谐波的边带，而正常状态边带不突出，与仿真信号对比验证了所建立模型的正确性。

4 结论

本文针对现有行星齿轮箱振动信号仿真模型的不足，结合现有模型的优势，以齿轮啮合冲击响应和齿轮啮合顺序为基础，开展了行星轮局部故障振动仿真建模研究，并对所建模型进行了实验及仿真验证，得出如下结论：

（1）使用单齿啮合冲击响应按照轮齿啮合顺序拼接，可以获得与实际振动波形接近的振动仿真模型。

（2）行星齿轮箱中包含多个啮合点，振动建模时仅考虑距离传感器较近的主要振源点便可包含振动信号的主要信息。

（3）行星齿轮箱中存在诸如齿轮、轴、轴承、行星架、箱体等部件，它们的固有频率各不相同，同时也存在齿轮箱整体的固有频率，造成振动信号中共振现象复杂，考虑包含多部件固有频率的振动仿真将是进一步完善模型的方向。

（4）通过对行星齿轮箱传动平台开展试验，以及对实测信号和仿真信号的对比分析，验证了所建立模型的正确性，为加窗振动分离等方法的验证和改进提供辅助与支撑。

参考文献：

[1]  Buzzoni M，Elia G，Cocconcelli M . A tool for validatingand  benchmarking  signal  processing  techniques  applied to machine diagnosis[ J ]. Mechanical Systems and Sig⁃ nal Processing，2020，139：106618.

[2]  Lei Y，Han D，Lin J，et al . Planetary gearbox fault di⁃agnosis  using  an  adaptive  stochastic  resonance  method [ J ]. Mechanical Systems and Signal Processing，2013，38（1）：113⁃124.

[3]  Randall R B . A new method of modeling gear faults[J ].Journal of Mechanical Design，1982，104（2）：259⁃267.

[4]  Feki N，Karray M，Khabou M T，et al . frequency anal⁃ysis of a two⁃stage planetary gearbox using two different methodologies[ J ]. ComptesRendusMecanique，2017：S163107211730205X .

[5] 冯志鹏，褚福磊，左明健.行星齿轮箱振动故障诊断方法[M].北京：科学出版社，2015.

FENG Zhipeng，CHU Fulei，ZUO Mingjian . Vibration Fault Diagnosis Method of Planetary Gearbox[M]. Bei⁃ jing：Science Press，2015.

[6] 雷亚国，汤伟，孔德同，等.基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断[ J ].机械工程学报，2014，50（17）：61⁃68.

LEI Yaguo，TANG Wei，KONG Detong，et al . Vibra ⁃ tion  signal  simulation  and  fault  diagnosis  of  planetary gearboxes based on transmission mechanism analysis[J ]. Journal of Mechanical Engineering，2014，50（17）：61⁃68.

[7]  McFadden P D . A technique for calculating the time do⁃main  averages  of the  vibration  of the  individual  planet gears and the sun gear in an epicyclic gearbox[ J ]. Jour⁃ nal of Sound and Vibration，1991，144（1）：163⁃172.

[8]  Guo  Y ，Zhao  L ，Wu  X ， et  al . Vibration  separationtechnique based localized tooth fault detection of plane? tary  gear  sets ：a  tutorial[ J ]. Mechanical  Systems  and Signal Processing，2019，129：130⁃147.

[9] 赵磊，郭瑜，伍星.基于包络加窗同步平均的行星齿轮箱特征提取[J ].振动、测试与诊断，2019，39（2）：320⁃326.

ZHAO Lei，GUO Yu，WU Xing . Fault feature extrac ⁃ tion of planetary gearboxes based on angle domain win⁃ dowed  synchronous  average  of the  envelope  signal[ J ]. Journal of Vibration，Measurement & Diagnosis，2019，39（2）：320⁃326.

[10]丁康，陈健林，苏向荣.平稳和非平稳振动信号的若干处理方法及发展[J ].振动工程学报，2003，16（1）：1⁃10.

DING  Kang，CHEN  Jianlin，SU  Xiangrong . Develop⁃ ment in vibration signal analysis and processing methods [ J ]. ，2003，16（1）：1⁃10.

[11]胥永刚，赵国亮，马朝永，等.双树复小波和局部投影算法在齿轮故障诊断中的应用[ J ].振动工程学报，2015，28（4）：650⁃656.

XU  Yonggang，ZHAO  Guoliang ，MA  Chaoyong，et al . Application of gear fault diagnosis method based on dual⁃tree  complex  wavelet  transform  and  local  projec⁃ tive  method [ J ]. Journal  of  Vibration  Engineering，2015，28（4）：650⁃656.

[12]姚文席，魏任之.渐开线直齿轮的非线性振动[ J ].中国矿业大学学报，1989，18（2）：4⁃11.

YAO Wenxi，WEI Renzhi . Nonlinear vibration of invo ⁃ lute spur gear [ J ]. Journal of China University of Min⁃ ing& Technology，1989，18（2）：4⁃11.

[13]姚文席，魏任之.渐开线直齿轮的啮合冲击响应[ J ].振动、测试与诊断，1992，12（2）：31⁃34.

YAO Wenxi，WEI Renzhi . Meshing impact response of involute  spur  gear [ J ]. Journal  of  Vibration，Measure ⁃ ment& Diagnosis，1992，12（2）：31⁃34.

[14] Chaari F，Fakhfakh T，Haddar M . Dynamic analysis ofa planetary gear failure caused by tooth pitting and crack⁃ ing [ J ]. Journal  of  Failure  Analysis  and  Prevention，2006，6（2）：73⁃78.

[15] Lewicki D  G，Samuel P D，Conroy J K，et al . Plane ⁃tary transmission diagnostics[ R ]. NTRS-NASA Tech ⁃ nical Reports Server，NASA/CR-2004-213068.

[16]赵磊，郭瑜，伍星.基于振动分离信号构建和同步平均的行星齿轮箱轮齿裂纹故障特征提取[ J ].振动与冲击，2018，37（5）：142⁃147.

ZHAO Lei，GUO Yu，WU Xing . Fault feature extrac ⁃ tion of gear tooth crack of planetary gear⁃box based on constructing  vibration  separation  signals  and  synchro⁃ nous  average [ J ]. Journal  of  Vibration  and  Shock，2018，37（5）：142⁃147.

Vibration simulation and experiment of planetary gearbox with planetary gear local fault

FAN Jia‑wei，GUO Yu，WU Xing，LIN Yun，CHEN Xin

（Faculty of Mechanical and Electrical Engineering，Kunming University of Science and Technology，Kunming 650500，China）

Abstract： In order to solve the problem that wavelet transform and windowed vibration separation technology are not effective in fault diagnosis of existing planetary gearbox local fault vibration simulation models，a planetary gear local fault vibration simulation model based on gear meshing impact response and gear meshing sequence is proposed . The single meshing impact vibration re⁃ sponse of normal teeth and fault teeth is simulated，and the time points of each gear engagement are calculated . The single meshing impact response is used to splice according to the gear meshing sequence . Considering the time-varying transmission path of the vi? bration signal and the modulation effect of the rotation frequency of the sun gear，planetary gear and planetary carrier，the local fault vibration simulation model of the planetary gear to meet the fault feature extraction of the windowed vibration separation tech ⁃ nology is established . The correctness of the model is verified by analyzing and comparing with the simulated and measured vibra⁃ tion signals collected on the planetary gearbox test platform .

Key words ： fault diagnosis；planetary gearbox；vibration signal simulation；windowed vibration separation method

作者简介：樊家伟（1994—），男，博士研究生。电话：18829898005；E ⁃mail：342774912@qq .com。

通讯作者：郭瑜（1971—），男，教授。电话：15911509207；E ⁃mail：kmgary@163.com。