频域组稀疏滚动轴承特征提取方法

王华庆 刘泽源 卢威 宋浏阳 韩长坤

摘要：针对时域非平稳振动信号模式混叠、信噪比低，以及传统稀疏表示算法模型复杂、优化求解算法难以确定，导致故障特征提取难的问题，提出了频域组稀疏和群桥约束改进迭代收缩阈值优化的故障特征提取方法（Group Sparse Representation in Frequency Domain，GSRF）。将振动信号转换至频域并对变量分组，构造施加群桥约束的最小二乘回归模型，准确筛选冲击相关变量；引入迭代重加权系数简化方程，以软阈值收缩优化求解频域稀疏信号；对重构的时域稀疏信号进行包络频谱分析提取故障特征。试验结果表明，提出的频域组稀疏算法优于传统的结合 L21范数约束的组稀疏索套方法，可有效提取微弱故障特征，实现稀疏域下的轴承故障诊断。

关键词：故障诊断；滚动轴承；微弱故障；稀疏表示；特征提取

中图分类号： TH165+.3；TH133.33    文献标志码： A    文章编号：1004-4523（2022）05-1242-08

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.022

引言

滚动轴承广泛应用在石化、军工等领域，作为机械设备的重要传动零件，轴承在高速重载的工况下容易发生损伤失效，影响设备正常运转，因此对轴承早期故障的監测和诊断至关重要[1]。分析振动信号以提取故障特征是常用的诊断方法[2] ，但恶劣工况和复杂传动系统往往使测得的振动信号呈现非高斯非平稳、模式混叠、信噪比低的特性，故障特征被噪声淹没[3]。因此从早期微弱轴承故障信号中提取特征信息具有重要意义。

稀疏表示在故障诊断方向应用广泛，求解过程可以大致分为确定数学模型和优化求解两部分[4]。其数学模型是范数约束的最小二乘逼近函数，Hou 等[5]对希尔伯特解调信号施加 L1约束增强了分解结果的稀疏性，实现了未知转速的轴承故障诊断。 Zheng 等[6]引入 L1、组2范数及无穷范数约束目标函数，在保证重构信号的稀疏性的同时提升了降噪效果，增强了早期微弱故障特征。优化求解算法可以大致分为贪婪算法、优化约束法、逼近算法、同伦算法。经典的贪婪算法包含由Mallat等提出的匹配追踪（Matching Pursuit，MP）及由 Pati 等改进的正交匹配追踪算法（Orthogonal  Matching  Pursuit， OMP），其重构信号往往是近似解[7⁃8]。优化约束法将原目标函数（不光滑或不可导等不易快速求解的问题）转换为光滑的或可求导问题，优化后的目标函数和原目标函数不同，简化了求解过程。其代表算法为梯度下降和交替方向乘子法（Alternating Direc⁃ tion of Method of Multipliers，ADMM）[9]。逼近算法将非光滑约束问题拆解为多个简单子问题，利用逼近算子分别求解这些子问题以提高求解效率。经典算法包括收缩算子、增广拉格朗日算法、受控极小化（Majorization Minimization，MM）、迭代收缩阈值算法（Iterative  Shrinkage ⁃ Thresholding  Algorithm ， ISTA）等[10⁃12]。

组稀疏回归模型在求解中协同约束组内、组间变量，促进分解的稀疏性。An 等[13]提出多尺度周期组索套，利用多级小波子带构建稀疏模型，通过 MM 优化非凸罚函数，在小波域提取周期脉冲，实现强噪干扰下的特征提取。Zhao 等[14]构建稀疏多周期组套索模型，使用 MM 解耦多重故障，实现了低信噪比复合故障信号的诊断。Zhao 等[15]基于增强稀疏组 Lasso 惩罚，自适应选择确定参数，并在 MM 优化中嵌入周期先验，直接提取时域脉冲，实现了微弱故障信号的诊断。

虽然上述方法成功提取了故障特征，但仍存在如下问题。1）模型过于复杂，多数模型为提升分解结果会引入多项罚参量，容易降低组内、组间变量选择的一致性。2）优化保凸能力弱，复杂非凸模型求解对优化算法要求高，当惩罚项不易平滑时将显著增加计算复杂度。

为解决上述问题，提出了基于频域的组稀疏特征提取方法，以组稀疏保证分解稀疏性的同时保留脉冲相关信息。轴承故障信号是故障特征信号与噪声的耦合信号，时域降噪难以实现解耦，将信号变换到傅里叶正交空间，有利于实现信号解耦，降低噪声，提取冲击信号。因此，先建立冲击敏感的数学模型并转换至频域的振动信号按组划分，再对分组后的频域信号施加群桥约束以选取冲击相关特征变量，引入迭代重加权系数，简化目标函数方程便于 ISTA 优化求解，最后重构稀疏时域信号，在包络谱上提取出信号故障特征。 GSRF 对同一惩罚项施加多种约束来保证变量筛选的一致性和稀疏性，利用权重系数凸优化回归模型，降低运算难度，通过对轴承早期故障信号的分析验证了所提方法的有效性。

1 基本原理

1.1 稀疏表示

用于生物信息、数理统计、信号处理等领域的数据维数通常很大，对信号做稀疏表示有利于缓解数据的存储、传输、提取的压力。稀疏表示简单理解为原信号是用少量基原子线性组合而成的[16]，即：

式中振动信号 Y ∈ Rn，观测矩阵 D∈ Rn × m 可为字典集或变换矩阵，稀疏系数 a ∈ Rm，噪声ε∈ Rn。

常用的稀疏表示模型可以总结为：

式中 p >0，惩罚系数λ>0。式（2）表示常用的范数约束求解，当 p=0时，是多项式复杂程度的非确定性问题，难以直接求解，Donoho与Candes等证明 p=1时，式（2）转变为索套算法（Least absolute shrinkage and selection operator，Lasso ），在满足一定稀疏性条件下，与p=0有同样的稀疏解。

1.2 桥组稀疏

传统 Lasso 算法仅能解决组内变量选择问题，稀疏性不强，Yuan 等在 Lasso 基础上引入组间变量选择，Huang 等又加入了桥惩罚项，进一步提高了运算速度与稀疏性，广泛应用在数据分析统计中[17⁃18]。

其原理为，对 n 维1列的信号 y =（y1，y2，…，yn ）′，有 n 维 d 列设计向量 Dk =（ D 1k，D 2k，…，Dnk ）′（k=1，…，d），A1，…，AJ 表示设计向量 D 的已知分组（1≤ J ≤ d），以aAj =（ak，k ∈Aj ）′表示第 j 组的回归系数，有桥组稀疏目标函数为：

式中惩罚系数λ>0，桥惩罚系数γ>0。式（3）是非凸问题，需转化为便于求解的凸函数。

1.3 迭代重加权

任意向量 e ∈ Rn，其p 范数可定义为：

对式（4）变形：

利用式（6）及权重 w 即可以将式（3）中的非凸问题转变为凸优化求解[19]。

1.4 近端算子

有函数f（x ）=g（ x ）+h（x ），其中 g（ x ）是可导凸函数，h（x ）不可导，其最小值可由迭代循环求解：

式中  t 为步长，常取李普希兹常数的倒数；∇g （ x ）为梯度。式（7）可写为不动点迭代形式：

式中prox稱为近端算子，在广义梯度下降更新求解中广泛应用，下文将结合迭代重加权的思想进一步优化约束。综上所述，确定了数学回归模型和优化求解算法，便可通过迭代运算求近似解。

2 基于频域组稀疏的特征提取

2.1 组稀疏

传统稀疏约束对向量内全部变量进行筛选，没有考虑变量间关系，组稀疏将 n 维向量 x 内变量分组，示意图如图1所示。

图1中，xgi表示第i组变量，每组变量数量可以根据信号特点划分，若不同组间无重复的变量可认为是非重叠组，反之认为是重叠组划分，即当i≠j 时，非重叠组中xgi与xgj无相同元素，重叠组中xgi与xgj有相同元素。重叠组稀疏不仅约束组内变量，还影响组间变量的选择，显著增强每次迭代对冲击相关变量的筛选能力，使重构时域信号具有更强的稀疏性[20]，冲击特征更明显。

为解决时域非平稳振动信号模式混叠、信噪比低及分解结果不稀疏的问题，将待处理信号转换到频域。引入重叠组稀疏后，数学回归模型写为：

式中 x 为待求解的稀疏信号，y 为转换至频域的原始振动信号，惩罚系数λ>0。2范数平方项保证重构信号和原信号的一致性，对组变量xg施加1范数约束以增强冲击特征选取能力[21]。

2.2 组桥约束

为进一步提高分解结果的信噪比，引入群桥约束组的变量[22⁃23]，式（9）写为：

式（3）中桥惩罚系数取0<γ<1时可以强化冲击相关变量的选择能力，此处依据经验选取群桥系数γ=0.5，但式（10）是非凸优化问题，结合1.3节介绍的迭代重加权，式（10）转化为：

上式形似式（2）的基础 Lasso 问题。据1.4节介绍，式（12）的前一项可视为 g（ x ），后一项可视为 h（x ），对 g（ x ）二阶泰勒展开并配方后，目标函数式（12）存在近端算子：

式（13）有数值解，更新可得稀疏信号 x。

2.3 基于频域桥组稀疏的故障诊断方法

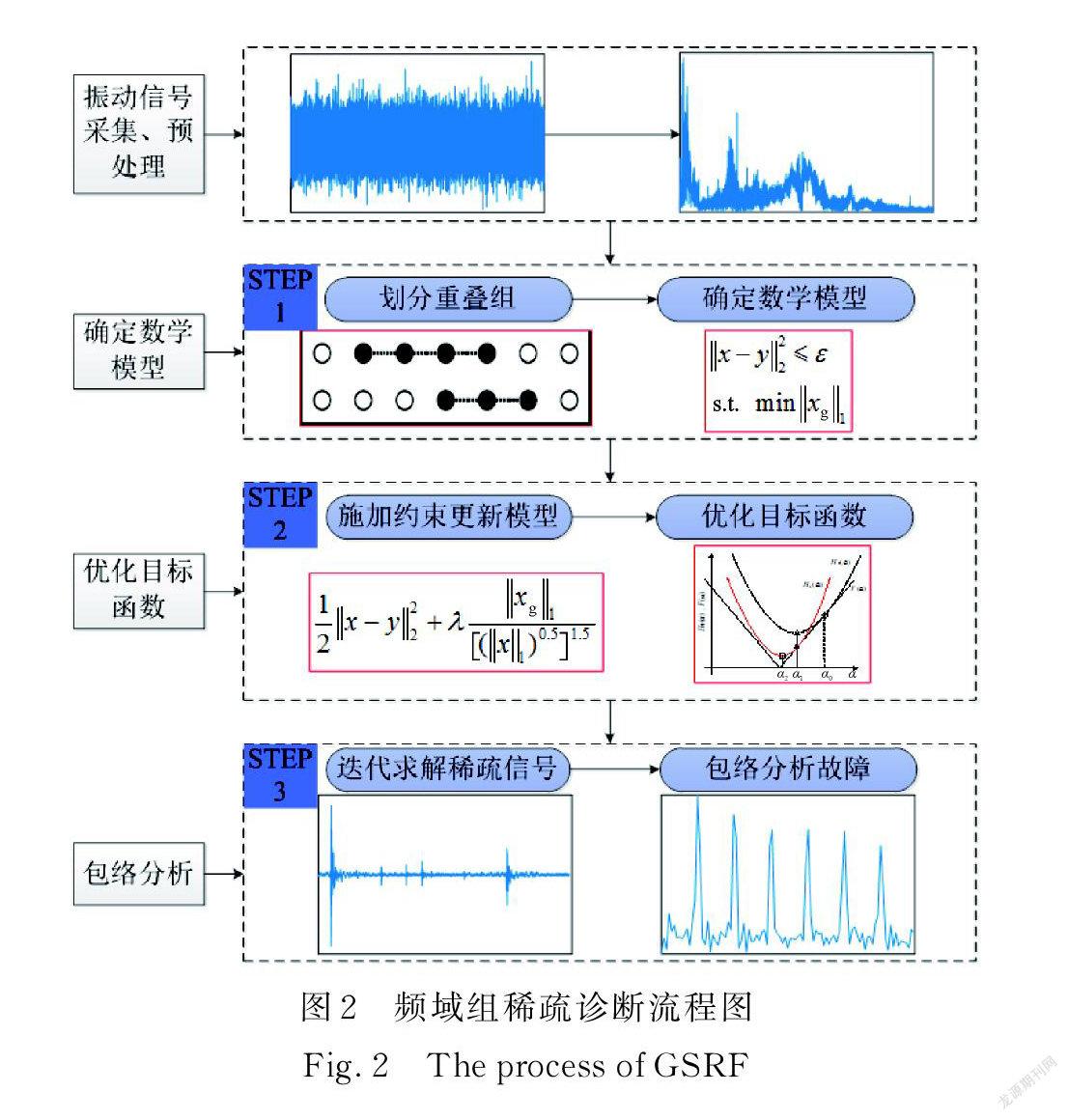
针对轴承的早期微弱故障，提出了以重叠组、群桥约束为基础的稀疏模型，以迭代重加权和迭代收缩阈值为优化算法的微弱故障特征提取方法，其具体实现步骤如图2所示流程图。

所提方法为减弱非平稳时域噪声干扰在频域进行特征提取，主要步骤如下：

（1）对转换到频域的振动信号内的变量按照重叠组划分，确定最小二乘结合 L1范数约束组变量的基础数学模型。

（2）施加群桥约束，进一步强化筛选冲击敏感的组间及组内变量，并引入迭代重加权系数简化目标函数，将非凸问题转化为形如加权 Lasso 的凸函数。

（3）对优化后的数学模型采用 ISTA 迭代更新求解频域稀疏信号，再转换回时域，最后对时域稀疏信号进行包络谱分析，提取故障特征频率，实现故障诊断。

3 实验分析与验证

为验证 GSRF 的有效性，分别采用公开轴承故障数据及课题组试验台数据，与传统非重叠组结合 L21范数约束的 Lasso 算法做了对比分析研究。

3.1 实验验证一

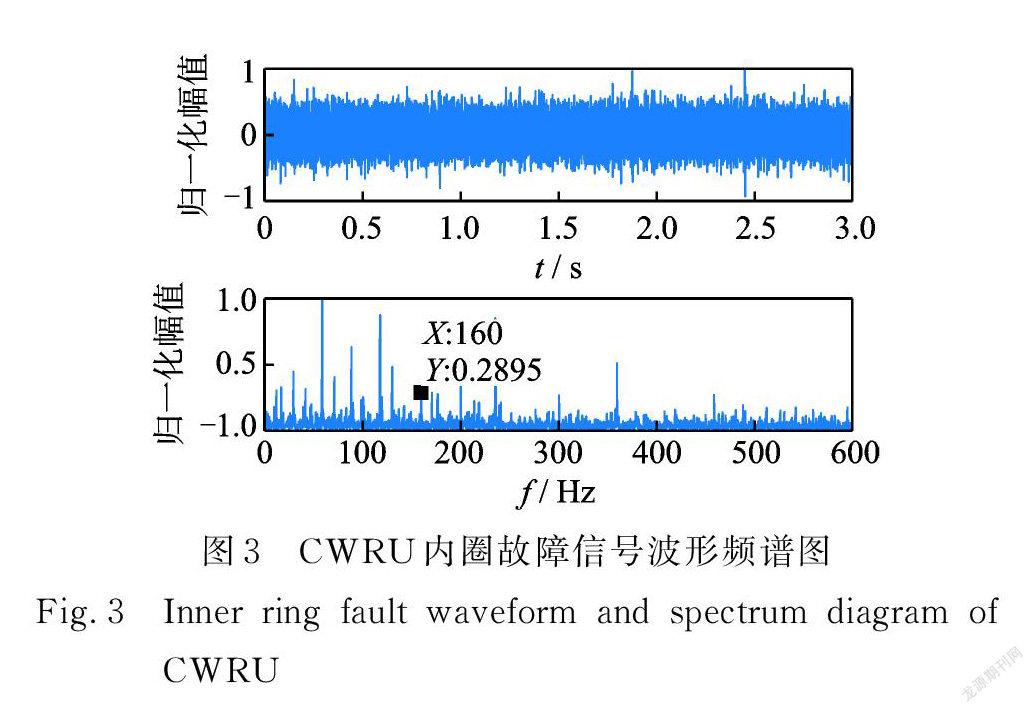
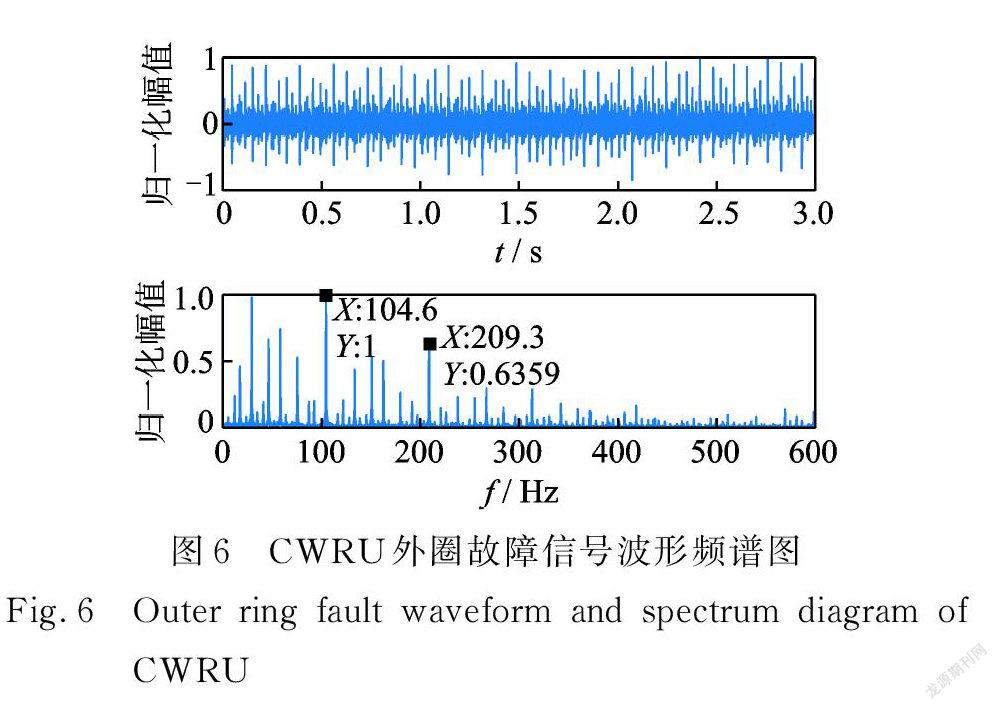
采用凯斯西储大学公开数据集中的 SKF 深沟球轴承，故障类型为内圈及外圈故障，采样频率12×103 Hz，内圈故障直径为0.014 in（0.356 mm），电机转速为1772 r/min，计算内圈故障特征频率约为159.9 Hz；外圈故障直径0.021 in（0.533 mm），电机转速1750 r/min，外圈故障频率约为104.55 Hz。

如图3所示，内圈故障特征频率完全被噪声淹没，分别以谱峭度、非重叠组结合 L21范数约束的 Lasso （传统方法）和频域群桥组稀疏（GSRF）做分析，图4为时域重构信号对比图，图5为包络谱对比。

所提方法综合考虑轴承转速、采样频率及频域分辨率的影响，选取频域信号的重叠组变量系数为20。图4中（ a ）为谱峭度，（b）为传统方法，（ c ）为 GSRF 。由图3和4对比可知，谱峭度和传统方法恢复的时域信号更稀疏，GSRF 处理后的时域信号与原始振动信号相比无明显变化。图 5（ a ）为谱峭度稀疏信号包络谱，（b）为传统方法稀疏信号包络谱， GSRF 包络谱如图（ c ）所示。对比包络谱，谱峭度和传统方法实现了故障特征增强，但对噪声成分的抑制效果较弱，GSRF 在增强故障特征的同时，较好地抑制了故障无关频率成分。

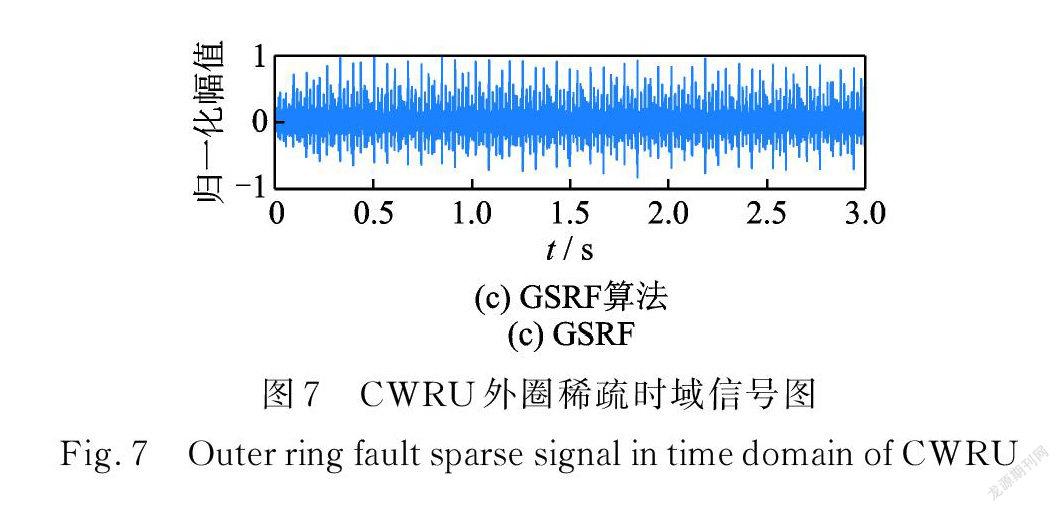
冲击明显，包络谱上特征频率受噪声干扰。图 7，8中（ a ），（b），（ c ）分别是谱峭度、传统方法及 GSRF 的分析结果。对比可知，传统方法处理后的信号在时域上更稀疏，GSRF 则在频域上消除了更多噪声干扰。综合分析认为 GSRF 在稀疏分解中尽可能多的保留了冲击信息，有效消除了故障无关成分的

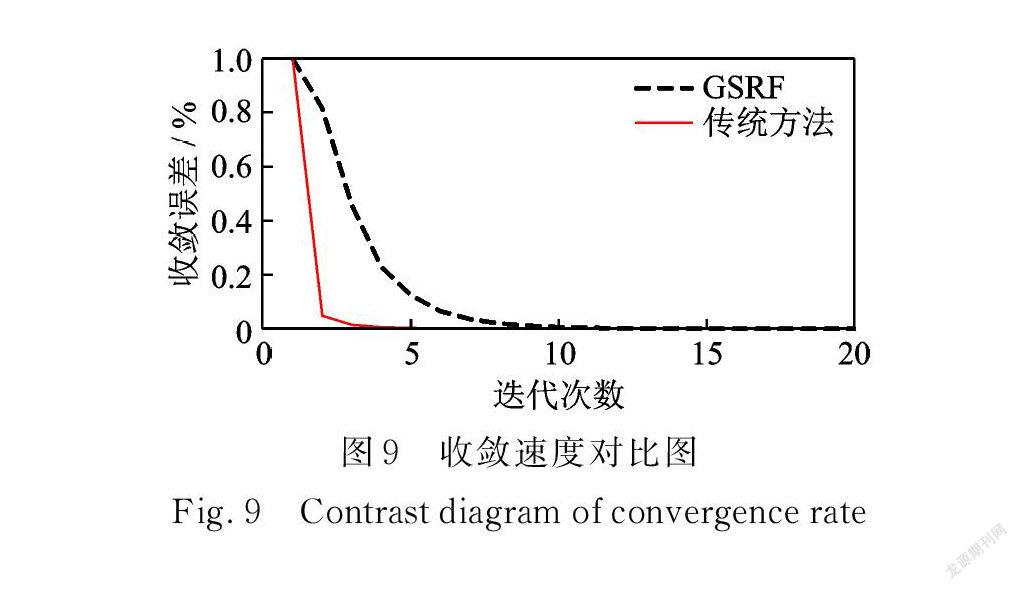
图9中，计算复杂的 GSRF 收敛相对更慢，也能在10步内收敛。表 1记录计算时间，分析认为 GSRF 对变量的细致筛选会降低运算速度，但却能显著提升诊断结果的准确性。

3.2  实验验证二

在如图10所示的试验台上采集振动信号，对 N205EM 圆柱滚子轴承做水平和竖直方向的数据采样，采样频率为105 Hz，电机转速为1300 r/min，线切割加工内、外圈故障宽度均为0.3 mm，深度为0.05 mm，计算内、外圈故障特征频率分别为145.84，86.32 Hz。

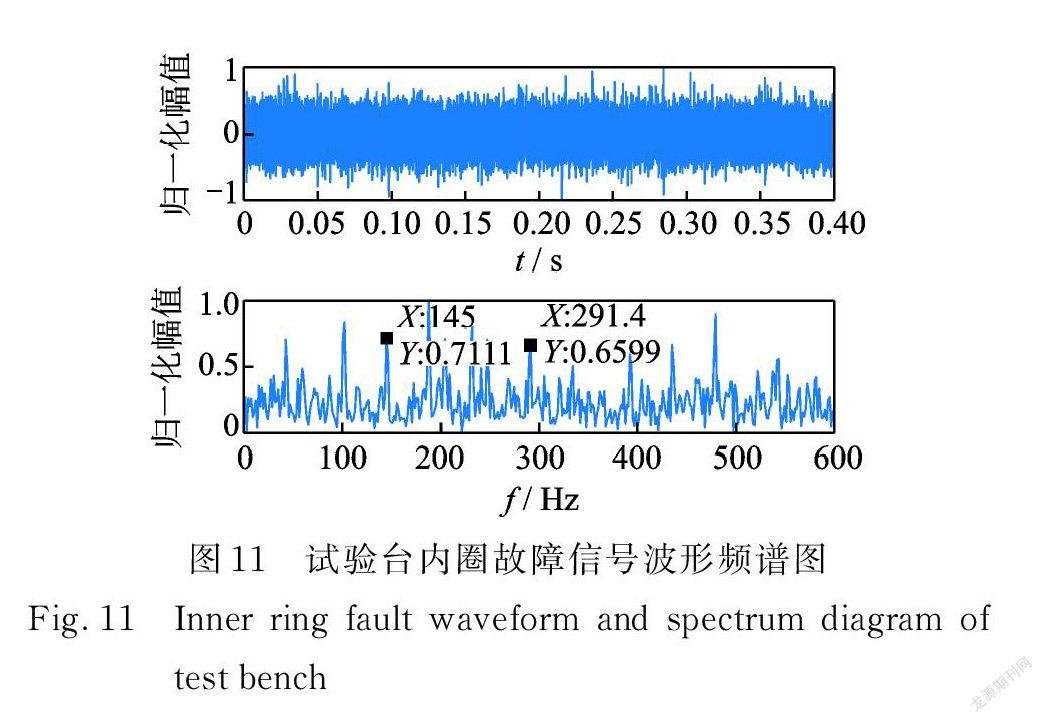
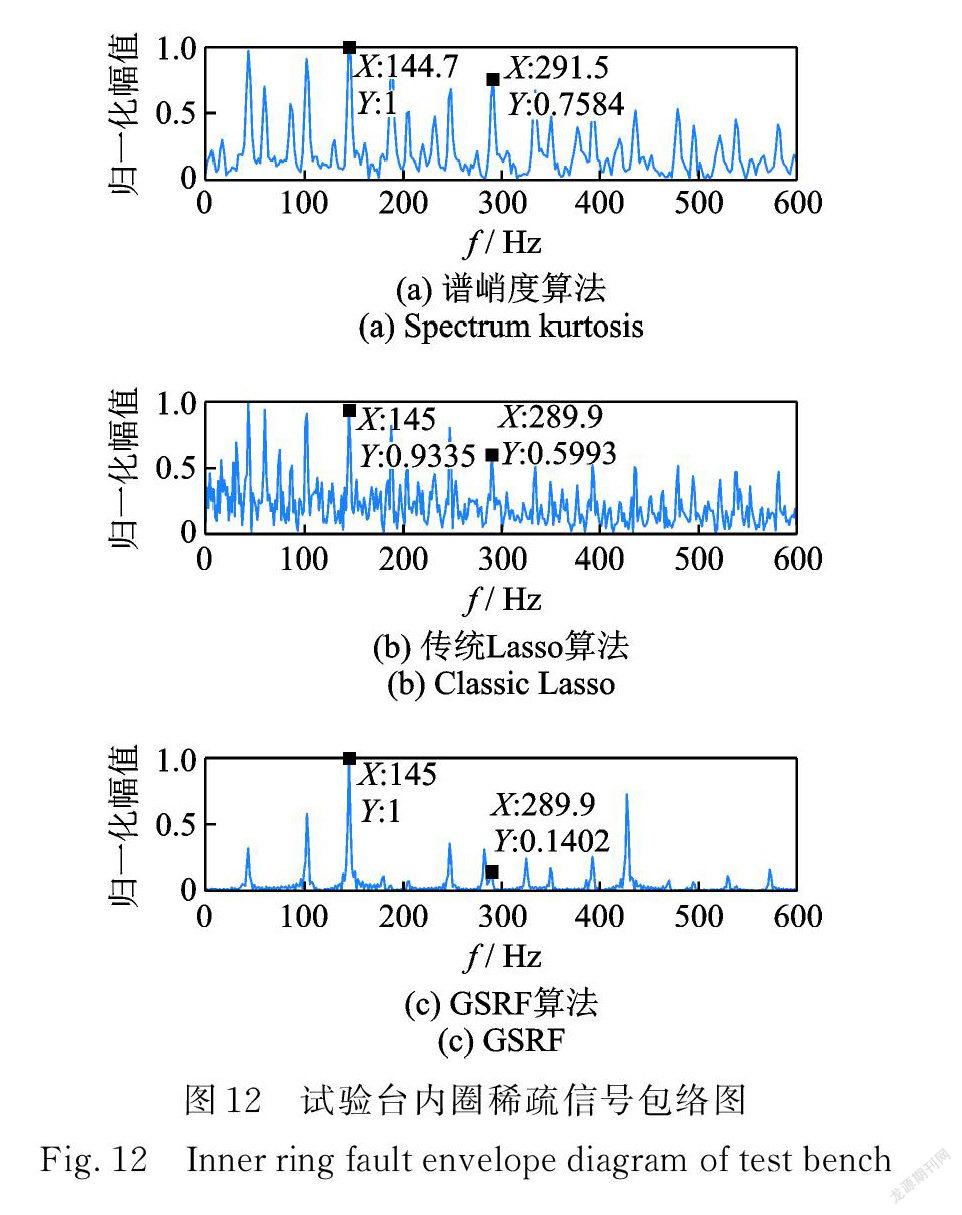
内圈故障信号时域频谱如图11所示，故障特征频率已被噪声淹没。综合考虑轴承转速、采样频率及频域分辨率的影响，对频域信号按每组20个变量划分重叠组，处理结果如图12所示。谱峭度和传统方法的包络谱分析在图12（ a ），（b）中故障特征频率较原信号有一定增强，但仍无法消除其他噪声成分的干扰，GSRF 处理的结果在图12（ c ）中则有效抑制了非平稳噪声。

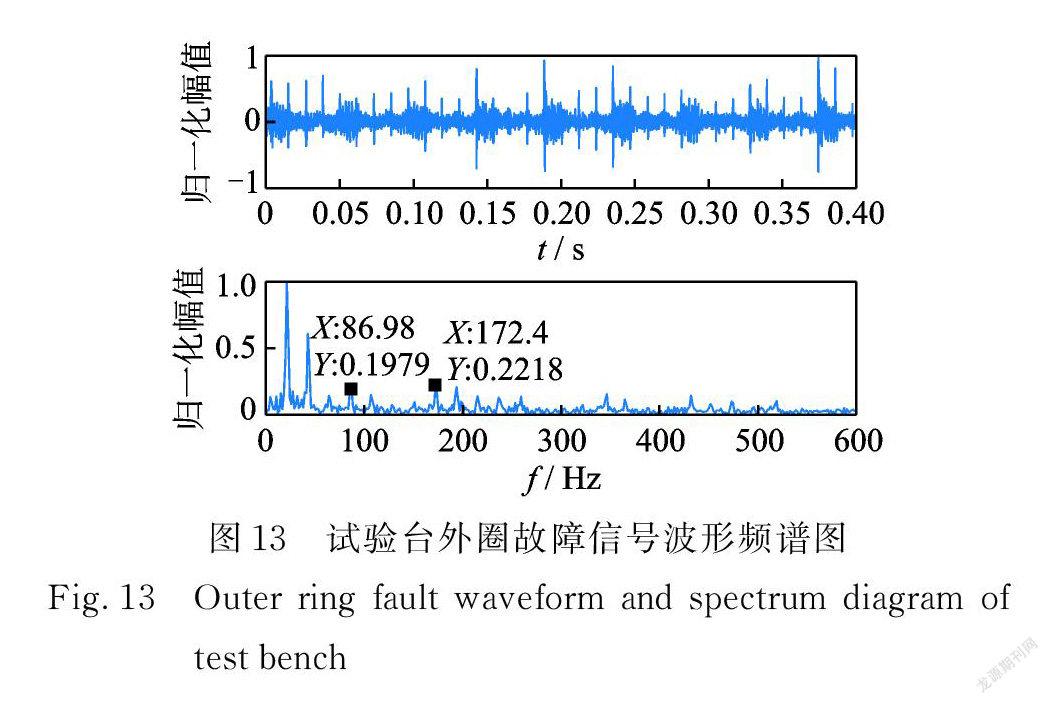
图13为外圈故障信号的波形频谱图，故障特征频率86.32 Hz 明显被淹没。图 14（ a ），（b）是分别应用谱峭度和传统方法处理后的结果，冲击特征频率及其高次谐波明显被增强，但无法消除旁瓣噪声的影响，在图14（ c ）中故障特征频率及其高次谐波明显且消除了干扰。表2为传统方法与 GSRF 计算时间对比结果，GSRF 在没有显著增加运算时间的情况下获得了更好的故障识别效果，实现了微弱故障的诊断。

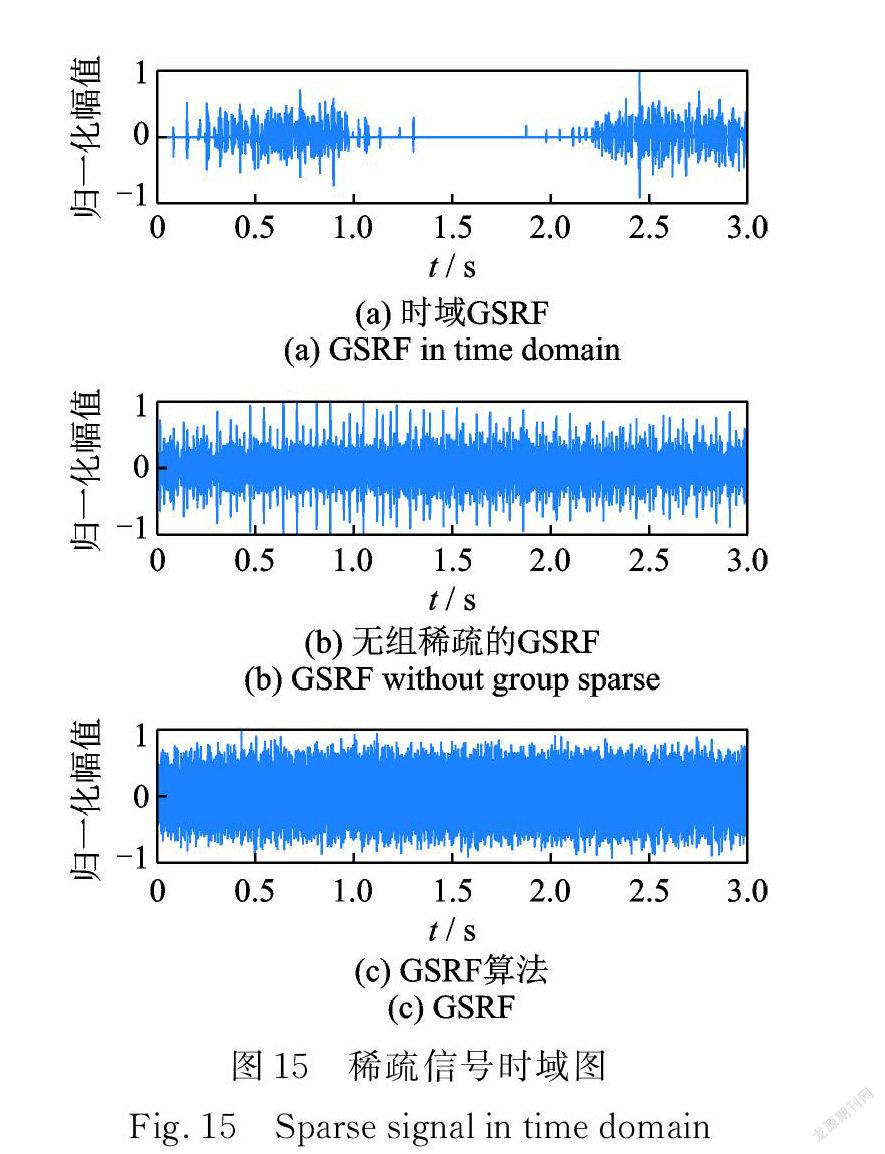
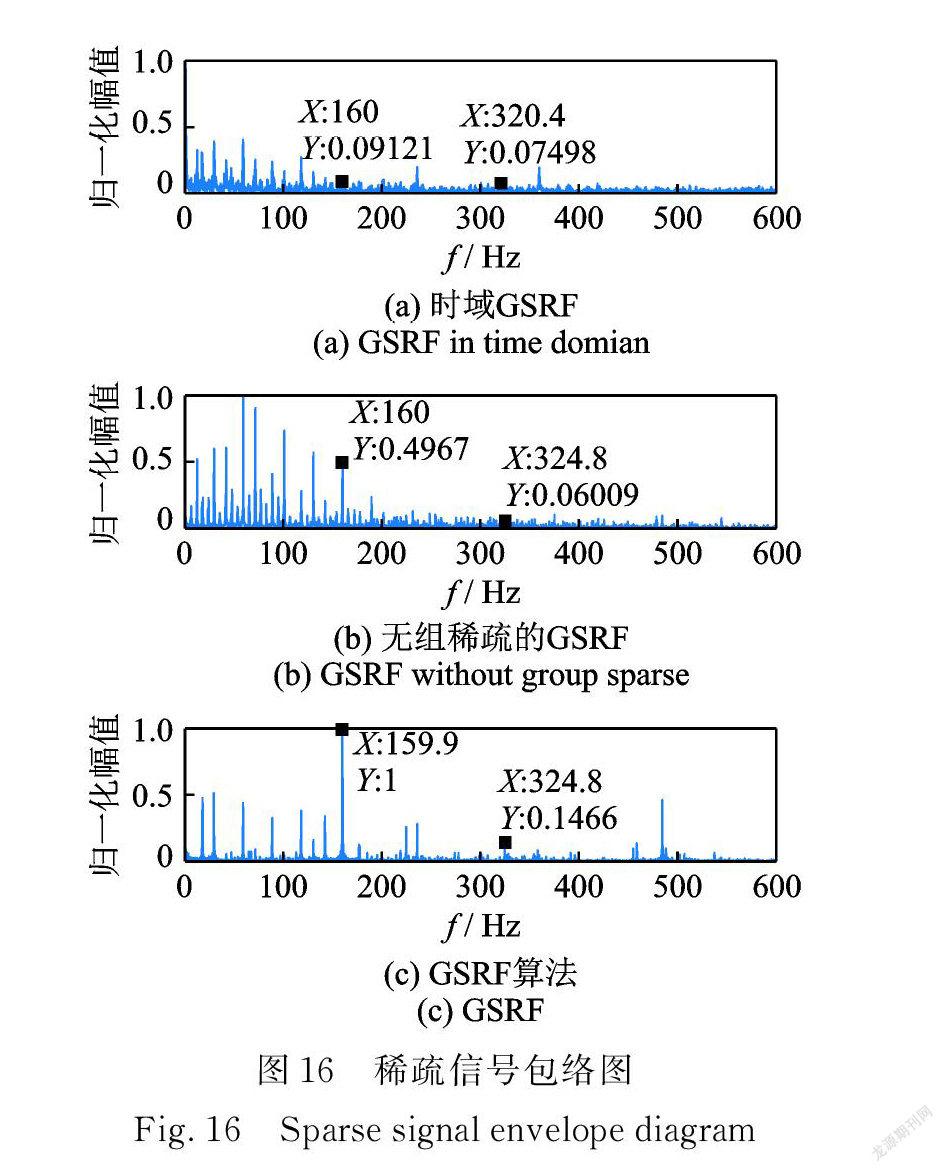
图15和16讨论了域变换和重叠组因素对分解结果的影响。图 15和16中：（ a ）是时域重叠组桥稀疏算法分解结果；（b）是频域无重叠组的桥稀疏算法结果，（ c ）是 GSRF 算法处理结果。

图15（ a ），16（ a ）显示，时域运算分解结果稀疏性较强，但故障信息丢失较多，对比图3，15（b）和16（b），无重叠组的桥稀疏算法增强了冲击特征，但无法实现信号与噪声的解耦，不能提取故障特征频率，而 GSRF 在增强故障特征的同时，抑制了故障无关频率成分，有效提取了故障特征频率。

4 结论

确定以最小二乘结合 L1范数约束的基础数学回归模型，根据故障信号冲击特点引入组稀疏及群桥约束，提出了基于频域组稀疏结合群桥约束的故障特征提取方法。实验分析结果表明：GSRF 将低信噪比信号转换至频域进行稀疏表示，可以减弱时域非平稳噪声扰动带来的模式混叠影响，提高了特征提取精度。组稀疏和群桥正则化按频率差别筛选组内、组间变量，在完整保留故障冲击信息的同时滤除了无关频率成分，进一步增强了故障特征。通过引入迭代重加权系数优化非凸目标函数，显著降低运算复杂度，便于使用 ISTA 求解。与传统非重叠组结合 L21范数约束的 Lasso 方法对比，验证了所提方法具有较强的特征提取能力和噪声鲁棒性。

参考文献：

[1] 陈是扦，彭志科，周鹏.信号分解及其在机械故障诊断中的应用研究综述[ J ].机械工程学报，2020，56（17）：91-107.

Chen Shiqian，Peng Zhike，Zhou Peng . Review of sig⁃ nal decomposition theory and its applications in machine fault diagnosis [ J ]. Journal of Mechanical Engineering，2020，56（17）：91-107.

[2] 魏永合，聂晨，李宏林. LMD 与优化 OMP 算法的滚动轴承故障诊断方法研究[ J ].沈阳理工大学学报，2020，39（3）：61-66.

Wei Yonghe，Nie Chen，Li Honglin . Study on fault di⁃ agnosis method of rolling bearing based on LMD and op⁃ timized  OMP  algorithm [ J ]. Journal  of  Shenyang  Li⁃ gong University，2020，39（3）：61-66.

[3] 李华，刘韬，伍星，等. EEMD 和优化的频带熵应用于轴承故障特征提取[ J ].振动工程学报，2020，33（2）：414-423.

Li  Hua ，Liu  Tao ，Wu  Xing ，et  al . EEMD  andopti⁃ mized frequency band entropy for fault feature extraction on  bearings [ J ]. Journal  of  Vibration  Engineering，2020，33（2）：414-423.

[4] 李清泉，王歡.基于稀疏表示理论的优化算法综述[ J ].测绘地理信息，2019，44（4）：1-9.

Li Qingquan，Wang Huan . Sparse representation-based optimization：a  survey [ J ]. Journal  of  Geomatics，2019，44（4）：1-9.

[5]  Hou F，Selesnick I，Chen J，et al . Fault diagnosis forrolling bearings under unknown time-varying speed con⁃ ditions with sparse representation[ J ]. Journal of Sound and Vibration，2021，494：115854.

[6]  Zheng  K ，Bai  Y ，Xiong  J ，et  al . Simultaneously  lowrank and group sparse decomposition for rolling bearing fault diagnosis[ J ]. Sensors，2020，20（19）：1-27.

[7]  Liang K，Zhao M，Lin J，et al . An  information-basedK-singular-value  decomposition  method  for  rolling  ele⁃ ment  bearing  diagnosis [ J ]. ISA  Transactions ，2020，96：444-456.

[8]  Zhang X，Liu Z，Wang L，et al . Bearing fault diagnosisbased  on  sparse  representations  using  an  improved OMP  with  adaptive  Gabor  sub-dictionaries [ J ]. ISA Transactions，2020，106：355-366.

[9]  Wang B，Liao Y，Ding C，et al . Periodical sparse low-rank  matrix  estimation  algorithm  for  fault  detection  of rolling  bearings [ J ]. ISA  Transactions ， 2020， 101：366-378.

[10] Zheng  Kai ，Yang  Dewei，Zhang  Bin ，et  al . A  groupsparse representation method in  frequency domain with adaptive  parameters  optimization  of&nbsp; detecting  incipient rolling  bearing  fault [ J ]. Journal  of  Sound  and  Vibra ⁃ tion，2019，462：114931.

[11] Zhang W，Yu D，Yan X，et al . Weak multiple fault de⁃tection  based  on  weighted  morlet  wavelet-overlapping group sparse for rolling bearing fault diagnosis[ J ]. Ap⁃ plied Sciences，2020，10（6）：2057.

[12] DiwuZhenkun，Cao Hongrui，Wang Lei，et al . Collab ⁃orative  double  sparse  period-group  Lasso  for  bearing fault diagnosis[ J ]. IEEE  Transactions on Instrumenta ⁃ tion and Measurement，2021，70：1-10.

[13] An B，Zhao Z，Wang S，et al . Sparsity-assisted bearingfault diagnosis using multiscale period group Lasso[ J ]. ISA Transactions，2019，98：338-348.

[14] Zhao  Z ，Wang  S ，Sun  C ，et  al . Sparse  multiperiodgroup  Lasso  for bearing multifault diagnosis[ J ]. IEEE Transactions  on  Instrumentation  and  Measurement，2019，69（2）：419-431.

[15] Zhao Z，Wu S，Qiao B，et al . Enhanced sparse period-group Lasso for bearing fault diagnosis[ J ]. IEEE Trans ?actions on Industrial Electronics ，2019，66（3）：2143-2153.

[16]王华庆，任帮月，宋浏阳，等.基于终止准则改进 K-SVD 字典学习的稀疏表示特征增强方法[ J ].机械工程学报，2019，55（7）：35-43.

Wang  Huaqing，Ren  Bangyue，Song  Liuyang，et  al .Sparse representation method based on termination crite⁃ ria improved K-SVD dictionary learning  for feature en⁃ hancement [ J ]. Journal  of  Mechanical  Engineering，2019，55（7）：35-43.

[17] Yuan M，Lin Y . Model selection  and  estimation in re ⁃gression with grouped variables[ J ]. Journal of the Royal Statistical Society：Series B，2006，68（1）：49-67.

[18] Huang J，Ma S，Xie H，et al . A group bridge approachfor  variable  selection [ J ]. Biometrika，2009，96（2）：339-355.

[19] Wang  X ，Wang  M . Adaptive  group  bridge  estimationfor high-dimensional partially linear models[ J ]. Journal of Inequalities and Applications，2017，2017（1）：1-18.

[20] Li  G ，Liu  X ，Chen  K . Integrative  multi-view  regres⁃sion：bridging  group-sparse  and  low-rank  models [ J ]. Biometrics，2019，75（2）：593-602.

[21] Park  C ，Yoon  Y  J . Bridge  regression ：adaptivity  andgroup selection[ J ]. Journal of Statistical Planning & In⁃ ference，2011，141（11）：3506-3519.

[22] Burrus C  S，Barreto J A，Selesnick I W . Iterative re ⁃weighted  least-squares  design  of FIR  filters [ J ]. IEEE Transaction on Signal Processing，1994，42（11）：2926-2936.

[23]刘建伟，崔立鹏，罗雄麟.组稀疏模型及其算法综述[ J ].电子学报，2015，43（4）：776-782.

Liu  Jianwei， Cui  Lipeng， Luo  Xionglin . Survey  on group sparse models and algorithms[ J ]. Acta Electroni⁃ ca Sinica，2015，43（4）：776-782.

Fault feature extraction using group sparse representation in frequency domain

WANG Hua-qing1，LIU Ze-yuan1，LU Wei2，SONG Liu-yang1，HAN Chang-kun1                  （1.College of Mechanical and Electrical Engineering，Beijing University of Chemical Technology，Beijing 100029，China；

2.Institute of Engineering Technology，Sinopec Catalyst Company Limited，Beijing 101100，China）

Abstract： A fault feature extraction method based on group sparsity and improved iterative shrinkage threshold optimization in fre ? quency domain （GSRF） is proposed to solve the issues in rolling bearing diagnosis about difficulty in mathematical model determi⁃ nation，sparse constraints and optimization algorithm selection . The vibration signals are converted into the frequency domain and the variables  are divided by  overlapping rules . The  least square regression model with  group bridge  constraint is  constructed to screen impact related variables accurately . The iterative reweighting coefficient is introduced to simplify the equation，so that the sparse signal in frequency domain can be solved by iterative shrinkage-thresholding algorithm . The envelope spectrum analysis of reconstructed sparse signal in time domain is carried out to extract the fault features . The experimental results show that the pro⁃ posed algorithm is superior to the traditional group sparse LASSO combined with L21 norm constraint . GSRF can effectively ex⁃ tract weak fault features and achieve bearing fault diagnosis in the sparse domain .

Key words ： fault diagnosis；rolling bearing；weak fault；sparse representation；feature extraction

作者简介：王华庆（1973—），男，教授。电话：13801023830；E-mail：hqwang@mail .buct .edu .cn。

通讯作者：宋浏阳（1988—），女，副教授。E-mail：xq _0703@163.com。