面向时变阻尼比-位移双目标的防屈曲支撑减震体系设计方法

吴 山，何浩祥，陈易飞

（北京工业大学工程抗震与结构诊治北京市重点实验室，北京 100124）

引言

结构消能减震技术是通过在主体结构的合适部位加入阻尼器，提供附加刚度和阻尼，从而起到提高结构抗震性能和安全性的作用。附加有效阻尼比是评价阻尼器减震效果的重要参数，合理确定附加有效阻尼比是消能减震设计的关键环节。

中国《建筑抗震设计规范》（GB 50011—2010）［1］规定采用阻尼器在结构预期位移下滞回一周耗能与减震体系在预期位移下的总应变能作比的方法计算附加有效阻尼比，可称为应变能法。该方法需要根据指定的阻尼器恢复力模型推算预期位移下的滞回耗能。文献［2］规定，防屈曲支撑（BRB）和软钢阻尼器应采用双线性模型或Bouc-Wen 模型模拟。吴克川等［3］推导并得到了预期位移下双线性模型滞回环面积解析解，在此基础上得到BRB 附加有效阻尼比计算公式。王维凝等［4］提出了理想弹塑性模型阻尼器的耗能表达式。尽管双线性模型被普遍用于BRB 的理论分析和有限元模拟，但由于其不能准确反映阻尼器的平滑屈服段特性，因此拟合精度较差，难以在各级位移下精确表征阻尼器耗能。Bouc-Wen 模型可以通过形状控制参数调控屈服段尖锐程度，从而准确表征多种类型阻尼器在平滑屈服段和各级位移下的滞回耗能［5-9］，因此研究该模型的能量解析表达具有重要的理论和工程意义。然而传统的Bouc-Wen 模型是隐式形式［10］，难以直接对其滞回环面积进行求解，因此目前尚无基于Bouc-Wen模型的附加有效阻尼比解析解，亟需对该模型滞回环面积进行解析推导，得到以BRB 为代表的位移型阻尼器阻尼比精确计算公式。

粗略的整体附加有效阻尼比可通过结构响应幅值求得，但幅值法计算结果往往大于真实值［11］。阻尼比与结构响应密切相关，且在时域是连续变化的。时变阻尼比不仅可以更加精确地表征减震性能，还能够反映阻尼比的变化规律和趋势。近年来，国内学者对时变阻尼比进行了大量研究工作。文献［12-15］将基于双线性模型的应变能法演变为时变方法，即分别计算每个时刻的时变附加有效阻尼比，并建议采用时变阻尼比均值评价减震效果。但按每个时刻计算能量并没有充分满足结构滞回耗能要求，计算精度较低。翁大根等［11］提出将阻尼器耗能与固有阻尼耗能作比计算附加有效阻尼比，即模态阻尼耗能法，该方法物理意义明确、计算精度高、操作简便且适用于各种类型的阻尼器，摆脱了应变能法在计算机理和阻尼器模型方面的局限，是一种优势明显的新计算方法。但目前该方法是对两种能量在整个时程内的累积结果作比，阻尼比的时变特性体现不充分，因此有必要对其进行改进［16］。

此外，目前的减震结构设计通常采用基于位移的设计方法，更关注结构安全性，但对结构减震性能的评估不够精细，缺乏对关键部位、楼层及整体的附加阻尼比精确和动态评估的方法，导致对阻尼器的选型、性能分析和量化评价并不全面，亟需提出更丰富的设计目标和方法。

鉴于此，本文对时变附加有效阻尼比计算方法进行研究及对Bouc-Wen 模型进行显式化解析，推导了滞回曲线面积解析解，进而提出基于该模型的应变能法计算公式；对模态阻尼耗能法进行改进，提出分时间段对阻尼器耗能和固有阻尼耗能进行求和后作比，更能体现阻尼比的变化趋势。之后对两种计算方法进行了对比，对时间段取值范围进行讨论。提出了以层间位移角和附加有效阻尼比为双目标进行减震设计的方法和流程。最后，结合采用BRB 的钢筋混凝土框架减震结构对定量阻尼比双目标设计方法的可行性和先进性进行了验证。

1 时变附加有效阻尼比计算公式

为了根据附加有效阻尼比进行结构减震设计，本文首先对阻尼比计算方法尤其是基于Bouc-Wen模型显式解的滞回能量解析计算进行研究。后文双目标设计需要根据每层层间位移角和附加有效阻尼比对该层阻尼器性能参数进行调控，因此在阻尼比算法中给出了每层附加阻尼比的计算公式。

1.1 基于Bouc-Wen 模型的应变能法

文献［1］规定的阻尼器附加给主体结构的有效阻尼比计算公式如下：

式中ζa为附加有效阻尼比；为第i个阻尼器在结构预期层间位移下往复循环一周所消耗的能量；Ws为减震体系在预期位移下的总应变能。

上述附加有效阻尼比计算方法采用结构响应幅值进行计算，属于包络法，结果偏于保守，精度较低［2］。此外，附加有效阻尼比与结构层间位移响应密切相关，因此在地震激励下是时变的，以每一时刻结构响应为依据，计算得到的时变附加有效阻尼比更符合实际情况，具有更高的精度。

假设高层结构每个楼层均为等效单自由度体系，根据式（1）可推得阻尼器提供的楼层时变附加有效阻尼比公式如下：

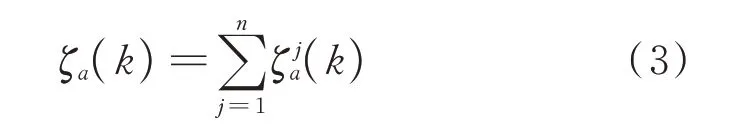
式中n为结构总楼层数。Ws(k)可通过下式计算：

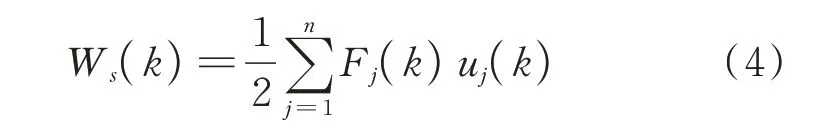
式中Fj(k)和uj(k)为第k时刻第j层结构体系层间剪力和层间位移。需要指出的是，式（1）中应为阻尼器滞回一周耗能，采用第k时刻阻尼器位移反推阻尼器滞回一周耗能是一种近似估算方法，因此建议对和Ws(k)的时程结果进行分段求和，求解时段内的附加有效阻尼比。

应变能法根据结构层间位移反推阻尼器预期位移下滞回一周耗能，因此须建立阻尼器位移和该位移下滞回耗能的计算公式，下面对第k时刻阻尼器在结构预期层间位移下滞回一周总耗能进行推导。阻尼器采用Bouc-Wen 模型模拟，假设一个楼层内采用的阻尼器力学特性均相同，则单个阻尼器时变的阻尼力-位移关系可用下式表示：

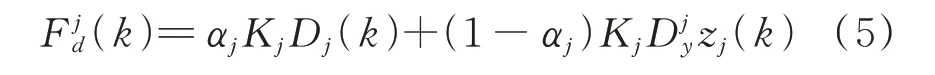
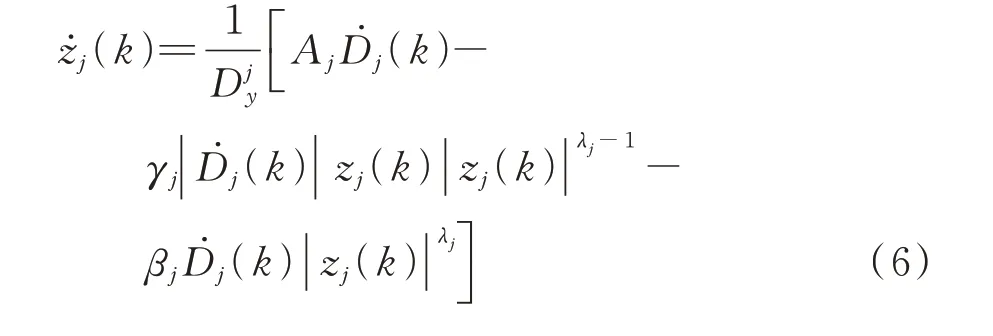
式中Aj，γj和βj为控制滞回曲线外形的参数，λj控制屈服尖锐程度。

假设BRB 与框架梁夹角为θ，则结构第k时刻第j层层间位移uj(k)与该层阻尼器轴向位移Dj(k)之间存在如下变换关系：

由式（5）和（6）表示的阻尼器阻尼力-位移关系为隐式表达式，难以直接对其在预期位移下滞回一周的能量求解，需先进行显式化解析。

令式（6）中的λj=1，去掉绝对值符号，用分段函数形式表示为：

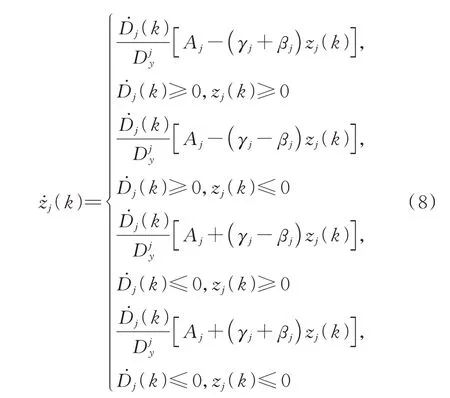
对上式进行变换得到内变量zj（k）和阻尼器轴向位移Dj(k)之间的微分表达式如下：

下面根据γj和βj的关系分别进行讨论。

（1）当γj≠±βj时，式（9）对Dj(k)积分可得：

式（12）对Dj(k)求积分，得到第j层第i个阻尼器的滞回环面积为：

（2）当γj=-βj时，式（9）通过对Dj(k)积分可得下式：

其中，

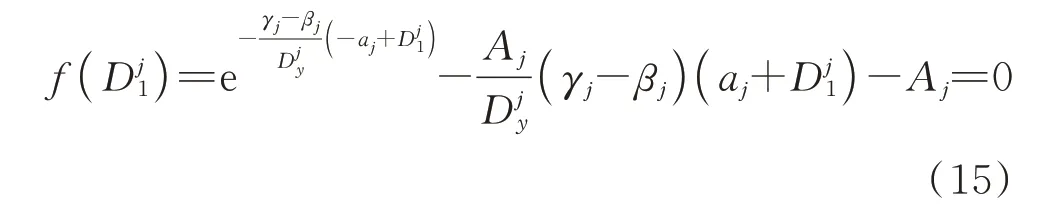
此时，第j层第i个阻尼器滞回环面积可通过积分得：

（3）当γj=βj时，式（9）通过对Dj(k)积分可得下式：

其中

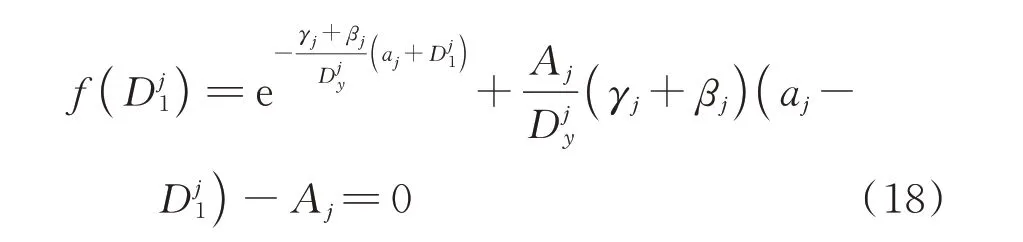
此时第j层第i个阻尼器滞回环面积为：

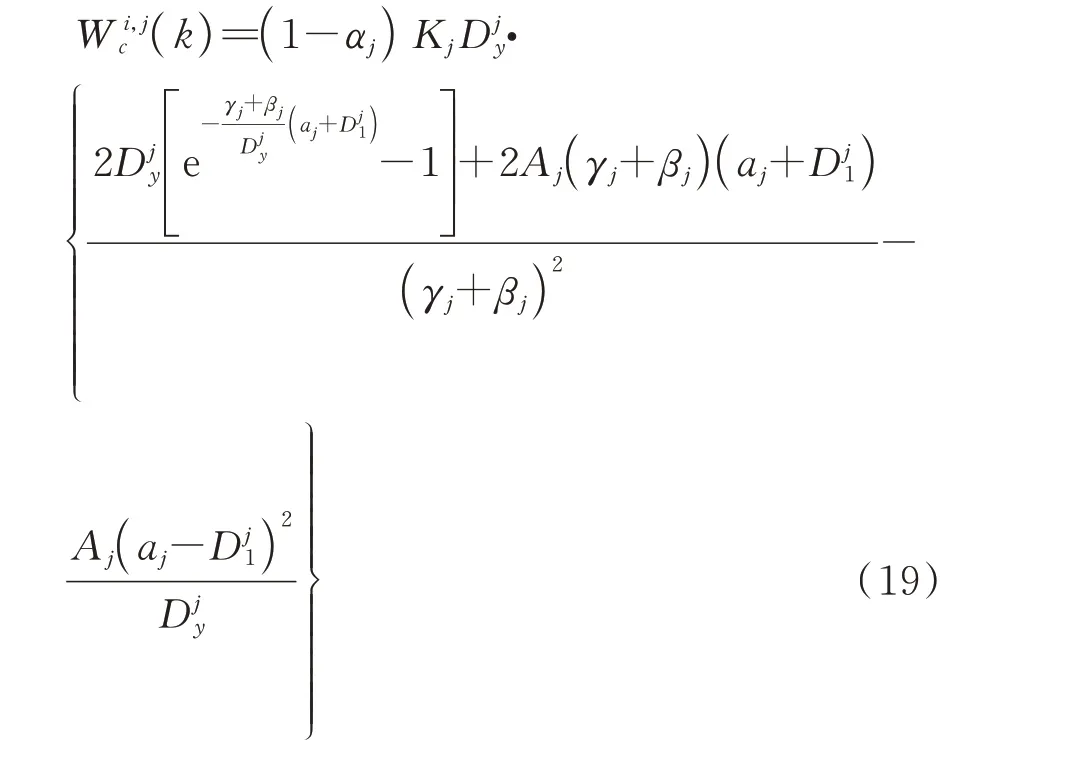
第j层阻尼器总耗能为：

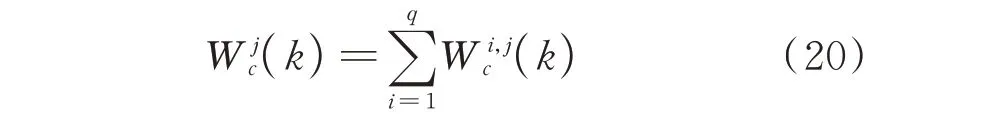
式中q为第j层阻尼器总数。

上文根据γj和βj的关系分情况推导了阻尼器在预期位移下滞回一周耗能解析解，计算附加有效阻尼比时应先对阻尼器荷载-位移曲线进行拟合，得到恢复力模型后根据γj和βj的关系选择滞回耗能表达式进行求解，在本文的BRB 模型中，γj=βj=0.5，即γj=βj的工况。选取合适的阻尼器滞回耗能公式后，根据结构层间位移计算，再根据层间剪力和层间位移计算减震体系总应变能Ws(k)，将两者代入式（1）计算附加有效阻尼比。

需要指出的是，该方法主要适用于计算BRB、金属阻尼器以及磁流变阻尼器等适合用Bouc-Wen模型表征的阻尼器附加有效阻尼比。

1.2 基于模态阻尼耗能法的附加阻尼比计算

为了克服传统应变能法求阻尼比需要指定的阻尼器恢复力模型且不完全适用于位移相关型阻尼器的局限，文献［11］提出一种基于模态阻尼耗能的时变附加有效阻尼比计算方法，但该方法在计算能量过程中积分区间存在一定缺陷。本文将对该方法进行改进和拓展。

消能减震体系的单自由度计算模型如图1所示。ks，cs和ms分别为主体结构的刚度、阻尼系数和质量，kd和cd分别为消能部件的刚度与阻尼系数。结构在地震作用下的动力方程为：

图1 消能体系单自由度计算简图Fig.1 Simplified diagram of the SDOF damping system

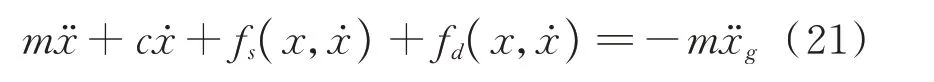
时变附加有效阻尼比可以表征任意时间段内阻尼器提供的阻尼比，进而准确评价阻尼器的动态减震效果。为了计算时变附加有效阻尼比，需要用时间段Td对地震动持时分段，对每一段分别求积分得到减震体系能量。将地震动持时按时段［k，k+Td］划分，其中k为时刻，并对式（21）各项在该时段内积分，获得单自由度体系的相对能量反应方程为：

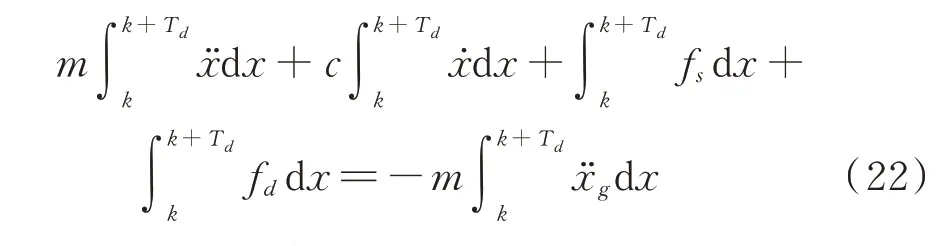
由于结构在真实地震下很少呈现完整的滞回曲线，并考虑到高阶振型周期的影响，Td可以取为结构第一阶自振周期T1的1.0～1.8 倍。将上式写为能量的形式，可进一步得到下式：

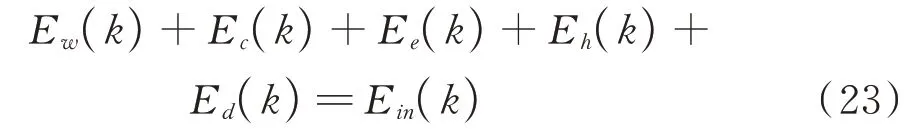
式中Ew（k）为结构动能；Ec（k）为结构固有阻尼耗能；Ee（k）为结构弹性应变能；Eh（k）为结构滞回耗能；Ed（k）为消能部件耗能；Ein（k）为地震输入能量。

由此可以得到n层减震结构体系在地震作用下的能量方程：

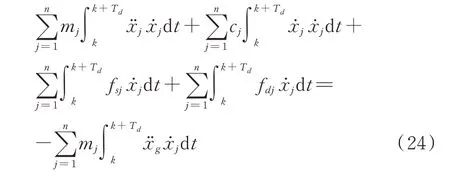
对于单自由度消能体系，基于能量等效原则，采用等效黏滞阻尼力做功表示阻尼器做功：

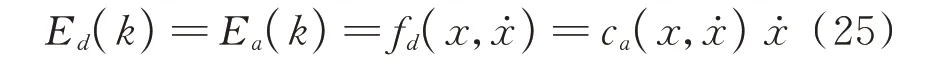
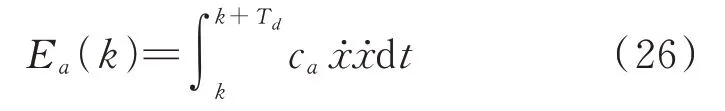
记ζ0为结构的固有阻尼比，阻尼器附加有效阻尼比为ζa(k)，由于阻尼比计算公式中结构势能对于ζ0和ζa(k)是一致的，故存在如下比例关系：

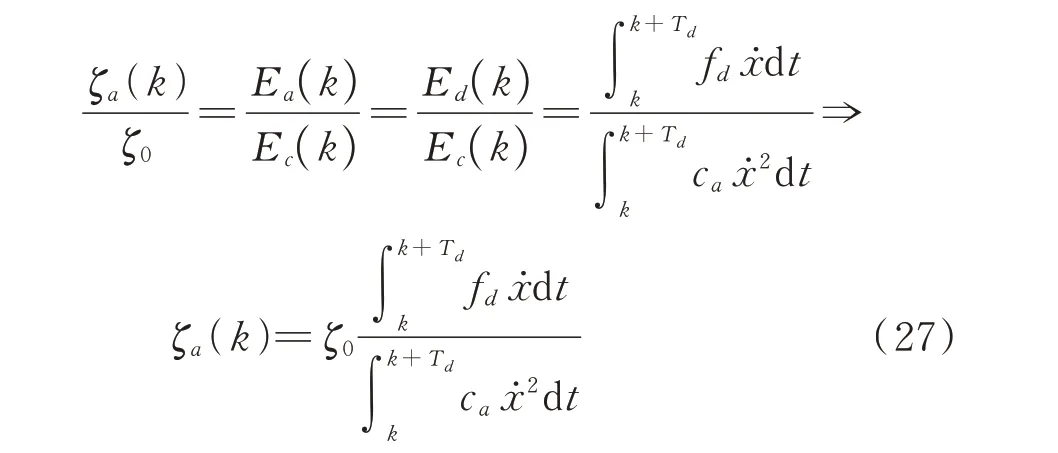
同理可得n层消能减震体系总附加有效阻尼比：

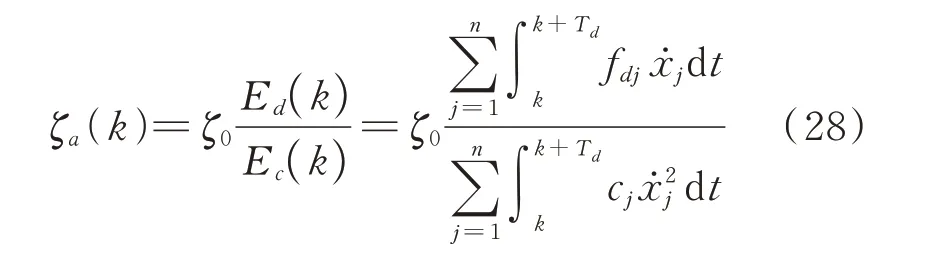
由上式可得消能减震体系第j层的阻尼器的附加有效阻尼比为：

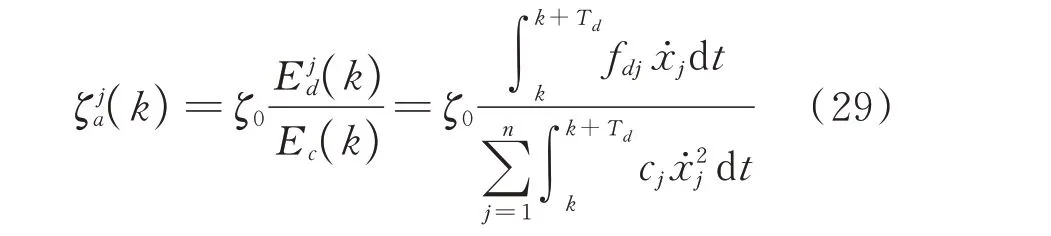
与应变能法相比，该方法不需要阻尼器恢复力模型，通过在有限元模型中提取能量即可求得附加有效阻尼比，因此该方法适用于所有类型的阻尼器，且计算精度高，计算简便。

2 双目标设计方法的设计流程

前文推导了两种阻尼比计算方法，下节对两者进行了比较，由于模态阻尼耗能法物理意义清晰，机理明确，计算精度高，因此在双目标设计中选用该方法计算阻尼比，工程设计中可根据需求对两种方法进行选择。需要指出的是，由于模态阻尼耗能法的机理具有普适性，因此该设计方法适用于采用各种阻尼器的减震结构，本节以BRB 减震体系为例进行展示。为了改进传统基于位移的设计方法难以充分考虑减震效果的不足，提出面向阻尼比-位移双目标设计方法流程如图2所示，采用两个基本设计目标：（1）各层层间位移角幅值θj小于层间位移角限值θ0；（2）减震结构总附加有效阻尼比ζa高于目标附加有效阻尼比ζa0。具体设计流程为：

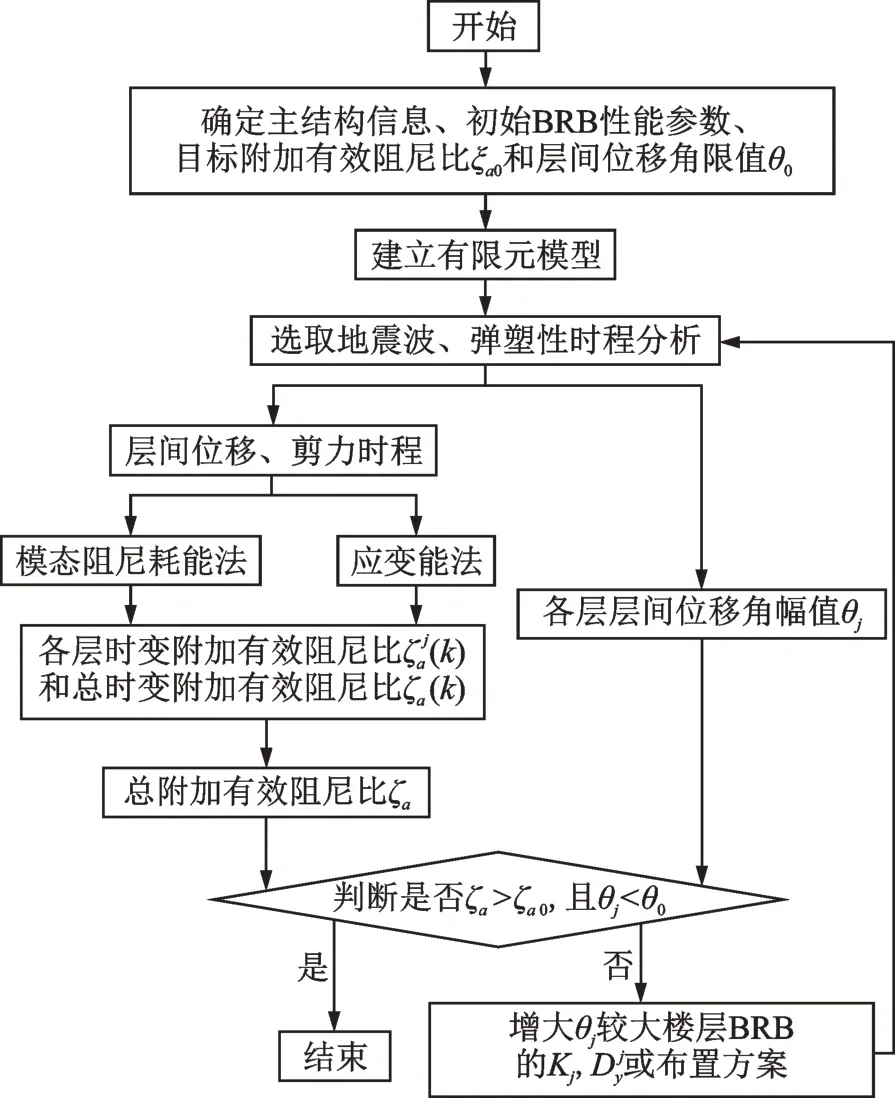
图2 双目标减震设计流程图Fig.2 Flow chart of double objective seismic design

（1）确定主体结构的层高、空间布局、梁柱配筋方案和材料性能等基本信息，BRB 的初始性能参数和布置方案，设定性能评价标准目标附加有效阻尼比ζa0和层间位移角限值θ0；

（2）基于有限元平台建立减震体系模型，选取合适的地震波对结构进行弹塑性时程分析；

（3）提取结构各层的层间位移和层间剪力时程，各层层间位移角幅值θj；

（4）根据时程结果，利用式（29）或式（1）～（20）（应变能法或模态阻尼耗能法）计算各层的时变附加有效阻尼比，进而得到总时变附加有效阻尼比ζa(k)，根据文献［11］建议，对总时变附加有效阻尼比ζa(k)取平均值，得到结构总附加有效阻尼比ζa；

（5）判断结构性能是否满足预期设计目标要求，若θj＜θ0，且ζa＞ζa0，则结构满足要求，设计结束，否则对层间位移角θj较大楼层的BRB 性能参数进行调整，通过增大Kj或的方法提高BRB 屈服力，达到增大该层BRB 附加有效阻尼比并减小层间位移角的目的，之后返回步骤（2）进行迭代计算。

3 算例分析

3.1 有限元模型

为了对比两种阻尼比计算方法，并验证面向阻尼比-位移双目标设计方法的有效性，选取一典型的含BRB 的钢混框架减震结构进行计算分析。该结构共8 层，每层高度为4 m。8 度抗震设防，场地类别为Ⅱ类，抗震等级为一级。设计地震分组为第二组，设计基本地震加速度值为0.15g。框架梁截面尺寸为700 mm×1000 mm，采用C30 混凝土，弹性模量为3.0×104MPa，抗压强度标准值为20.1 MPa，钢筋弹性模量为2.0×105MPa，屈服强度为413 MPa，极限强度为620 MPa，配筋率为0.96%；框架柱截面尺寸为900 mm×900 mm，采用C35 混凝土，弹性模量为31500 MPa，抗压强度标准值为23.4 MPa，配筋率1.62%。基于SAP2000 建立如图3所示有限元模型，梁柱采用杆系单元模拟，弹塑性变形用塑性铰单元模拟。无控结构第一周期为0.638 s。在初步设计方案中，每层沿两水平方向各布置4 个BRB 选用Plastic-Wen（Bouc-Wen）模型，SAP2000中该模型的γ，β，A和λ为固定值，分别为：0.5，0.5，1及1，可调整的参数如表1所示。

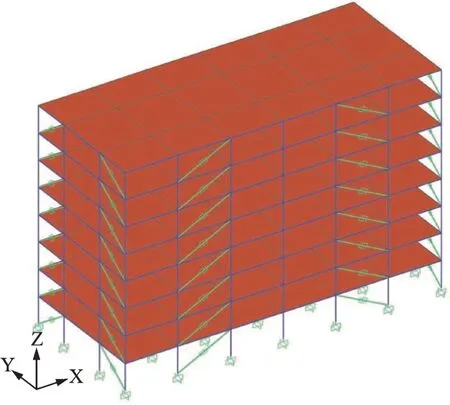
图3 框架结构有限元模型Fig.3 Finite element model of frame structure

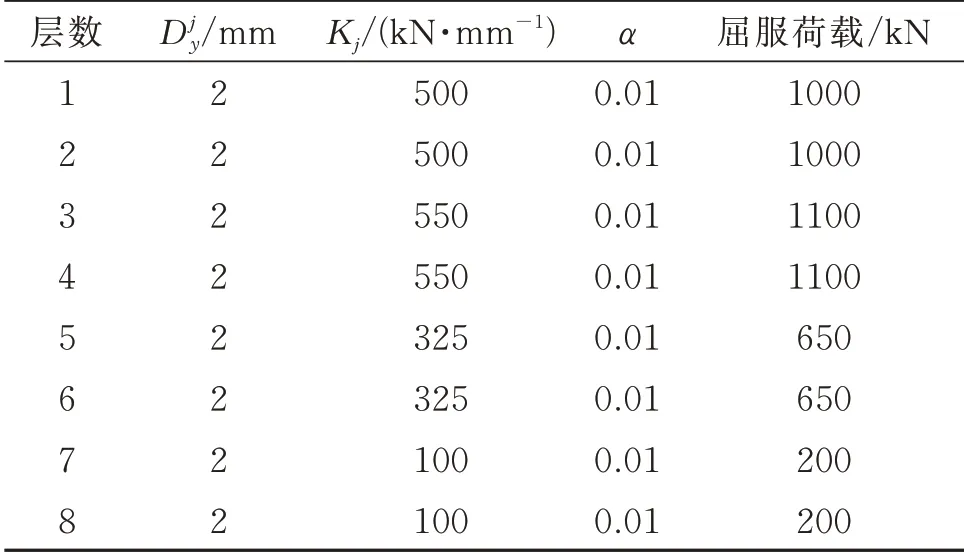
表1 BRB 初始性能参数Tab.1 BRB initial performance parameters

3.2 两种计算方法对比分析

对减震体系模型第一阶振型方向（Y方向）输入El Centro 波，并基于结构的响应采用式（1）和（28）分别计算BRB 提供的附加有效阻尼比，对结果进行对比分析。模态阻尼耗能法中的结构固有阻尼累积耗能和消能部件累积耗能均可在SAP2000 中直接提取，减震体系第一周期T1=0.566 s，Td取0.8T1，1.0T1，1.5T1和2.0T1，采用应变能法和模态阻尼耗能法分别计算结构时变附加有效阻尼比，其中应变能法中的阻尼器耗能和减震体系总应变能按照同样的时间段求和计算，两者对比结果如图4所示。

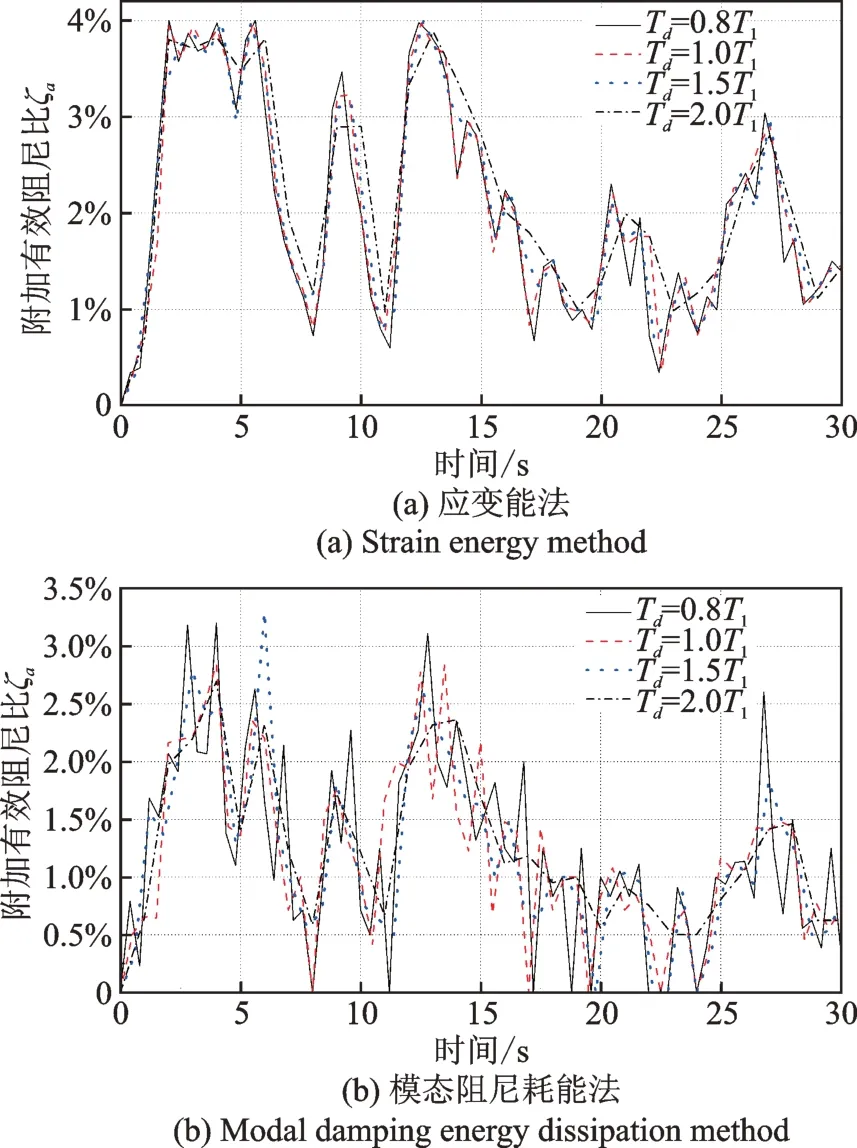
图4 应变能法和模态阻尼耗能法的计算结果Fig.4 Results of strain energy method and modal damping energy dissipation method

将两种方法得到的时变附加有效阻尼比变化趋势进行对比，可见两种附加有效阻尼比均在2.5 s 左右达到峰值，并具有类似的演变趋势，但基于模态阻尼耗能法的结果更加细致且幅值略小。当Td取不同值时两种方法得到的时变附加有效阻尼比平均值和最大值如表2所示。为了排除个别地震动为计算结果带来的偶然性，对结构输入3 条天然波和2 条人工波，按Td=1.0T1算得两种方法的结果如表3所示。可以看出，时间段Td对两种方法的平均值和应变能法的最大值影响较小，对模态阻尼耗能法的最大值影响相对明显。应变能法的平均值和最大值均大于模态阻尼耗能法的平均值和最大值。此外，文献［11］对时变附加有效阻尼比的取值问题进行了讨论，建议采用平均值来评价阻尼器的减震效果，本文结果表明平均值是稳定的，验证了该建议的合理性。

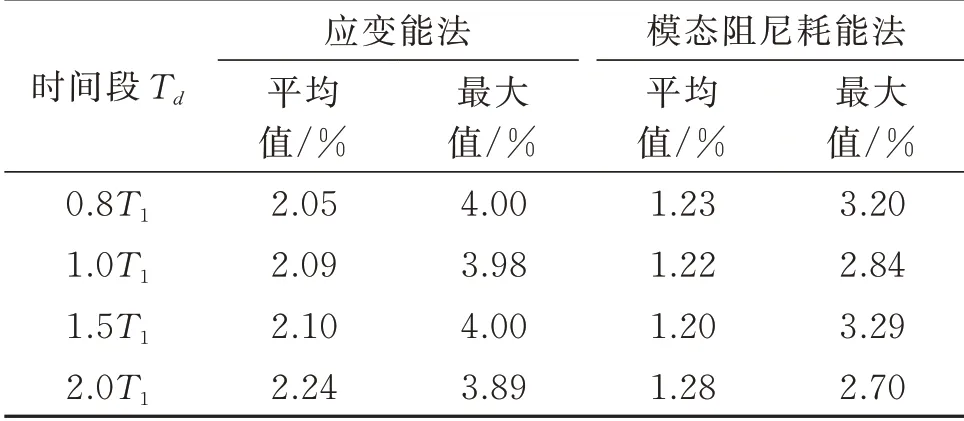
表2 不同方法的附加有效阻尼比对比Tab.2 Comparison of additional damping ratio obtained by different methods

表3 不同地震波下的附加有效阻尼比对比Tab.3 Comparison of additional damping ratio under different seismic waves

综上，应变能法可被视为一种近似估算方法，而模态阻尼耗能法物理意义明确，各能量表征准确，且对滞回耗能特性更敏感，故将该方法视为附加有效阻尼比的精确算法。此外，应变能法的结果偏大，阻尼器性能将被高估，是偏于不安全的。

3.3 模态阻尼耗能法的Td取值讨论

模态阻尼耗能法的本质在于对减震结构消能部件耗能和固有阻尼耗能分别在每个时间段Td内求和并作比，因此时间段Td的合理范围对求解精度起着至关重要的作用。从滞回耗能的机理来看，Td不能小于结构第一自振周期，但其上限值需要通过减震分析和经验来确定。以El Centro 波工况为例，取Td范围为0.5T1～2.0T1计算时变附加有效阻尼比，平均值和最大值如图5所示。应变能法的最大值偏大且对滞回时段不敏感，而模态阻尼耗能法的最大值与结构响应时变特性密切相关，准确地反映了考虑不同滞回时段长度下阻尼比的变化。随着时间段Td逐渐增大，两种方法平均值一直呈稳定状态，进一步验证了采用时变附加有效阻尼比平均值评价减震结构性能的合理性。经综合分析，认为Td的合理取值范围为1.0T1～1.8T1。

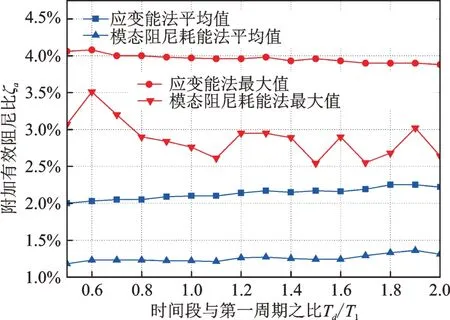
图5 时间段Td的影响Fig.5 Effect of time step Td

3.4 设计分析

对算例中的有限元模型按照图2 中的设计流程进行附加有效阻尼比定量设计。实际工程设计中，目标附加有效阻尼比ζa0应根据工程需求而定，本文取5%，层间位移角限值θ0取1/250。由于模态阻尼耗能法的物理意义明确且精度高，采用该方法计算结果的平均值作为耗能部件附加有效阻尼比取值。

根据选择实际反应谱与目标反应谱接近的3 条天然地震波作为地震激励。目标反应谱、3 条天然波的反应谱和平均谱如图6所示，RSN1489，RSN1511 和RSN1528 三条天然波均为1999年中国台湾集集地震，震级7.62，分别由TCU049，TCU076 和TCU101 站点测得。将3 条天然波峰值加速度（PGA）调幅至400 cm/s2，BRB 的附加有效阻尼比ζa取3 条波计算结果的平均值，各层层间位移角θj取响应时程最大值。

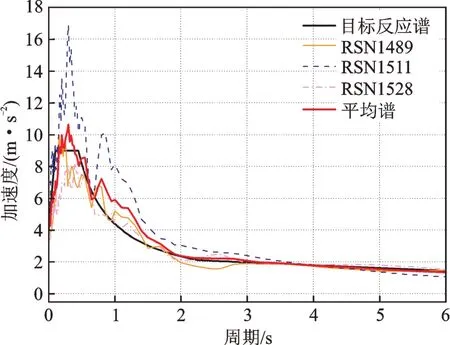
图6 目标反应谱和选取地震波的反应谱Fig.6 Target response spectrum and response spectrum of selected waves

将设计流程按迭代轮次进行展示和分析。

（1）减震体系的阻尼器初始性能参数见表1，通过式（28）和（29）计算得到的附加有效阻尼比如表4所示，各轮设计层间位移角幅值如图7（a）所示。

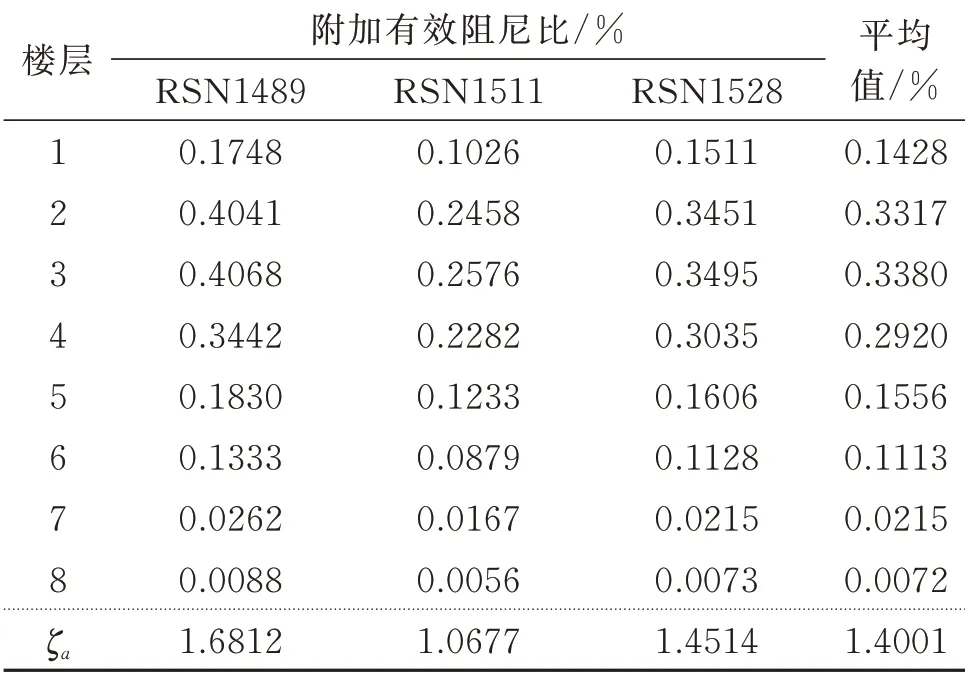
表4 第一轮设计的附加有效阻尼比Tab.4 Additional damping ratio of the first round design

图7 设计效果Fig.7 Design effect

由第一轮设计结果可知，BRB 提供的附加有效阻尼比为1.4%，与目标附加有效阻尼比5%存在较大差距，且2～4层层间位移角超限。采用保持其他参数不变，加大支撑弹性刚度的方式提高BRB 屈服力，进而提高附加有效阻尼比。结合层间位移角幅值选取调整阻尼器参数的楼层，1～6 层的层间位移角较大，下一轮应对这些楼层的BRB 弹性刚度进行加强，使结构变形更加均匀。考虑到8 层层间位移角较小，且该层BRB 提供的阻尼比较小，出于经济性考虑，将8层的阻尼器撤除。各轮设计的BRB 弹性刚度如表5所示，BRB 提供的附加有效阻尼比如表6所示。

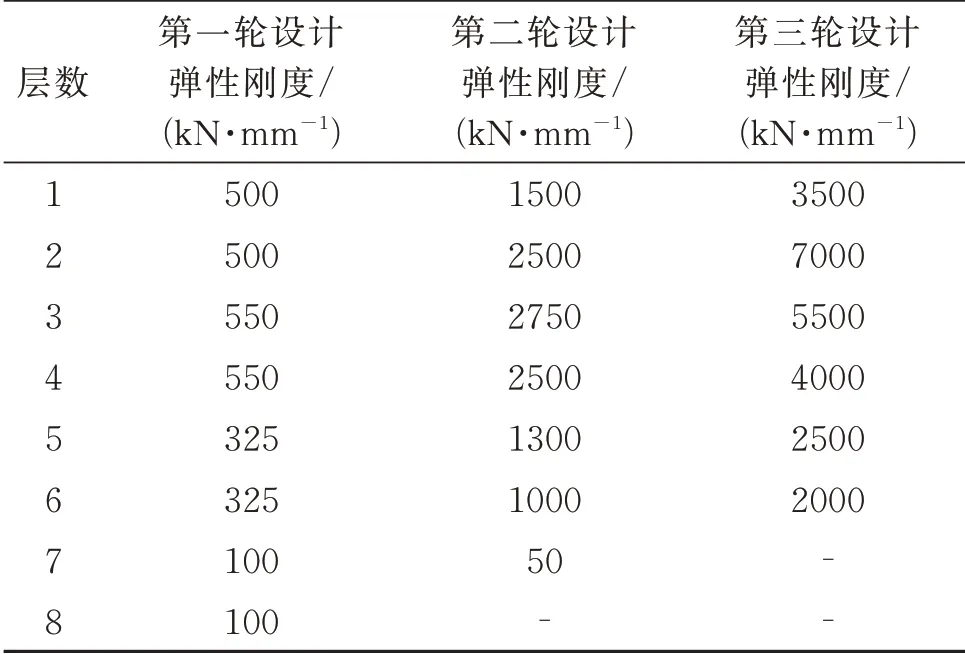
表5 各轮设计中BRB 的弹性刚度Tab.5 BRB elastic stiffness of the all rounds design

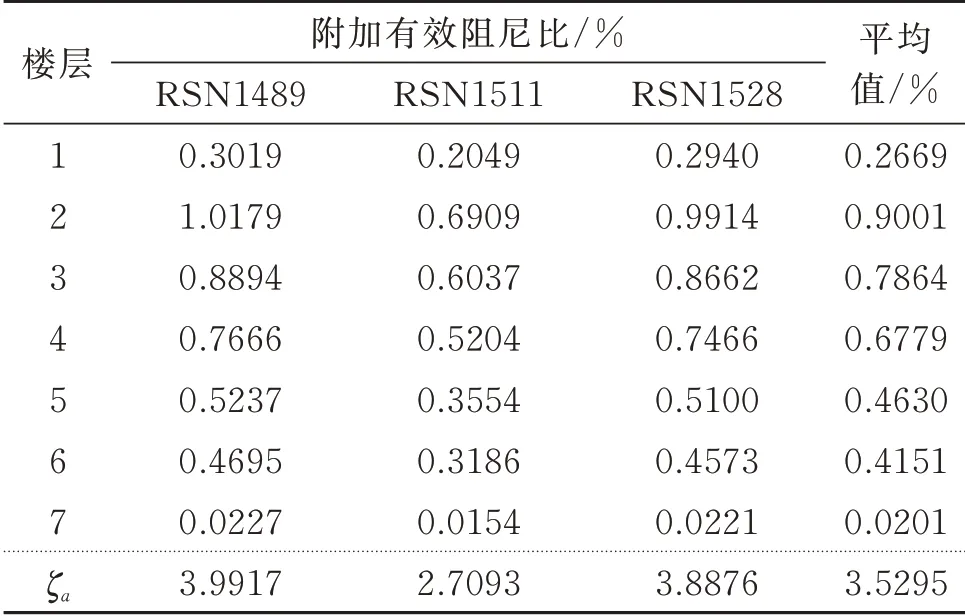
表6 第二轮设计的附加有效阻尼比Tab.6 Additional damping ratio of the second round design

（2）通过第二轮设计，附加有效阻尼比得到大幅提高，同时各层层间位移角幅值已符合要求，但阻尼比没达到预期目标，需要进行第三轮设计。

在第二轮设计中，层间位移角已满足要求，若采用传统基于位移的设计方法已可完成设计，但此时附加有效阻尼比仍然偏低，阻尼器的减震性能没有得到充分发挥。而面向阻尼比-位移双目标的设计方法对结构设计提出了更高的要求，可以进一步调控动力响应和减震性能，使结构体系具有更大安全储备。双目标之间是相互协调和促进的关系。

由于7 层阻尼器附加有效阻尼比较小，且层间位移角偏于安全，因此撤除该层阻尼器。考虑到2层层间位移角较大，出现变形不均匀现象，应着重加强该层阻尼器出力。

（3）第三轮BRB 提供的附加有效阻尼比如表7所示。可见附加有效阻尼比已经达到预期附加有效阻尼比，且层间位移角幅值小于层间位移角限值，设计流程结束。

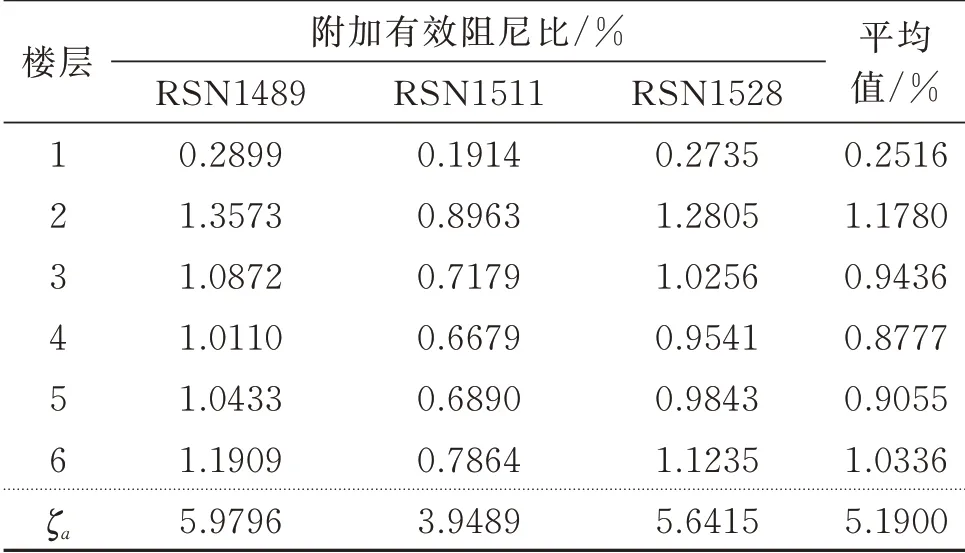
表7 第三轮设计的附加有效阻尼比Tab.7 Additional damping ratio of the third round design

经过优化调整，附加有效阻尼比大幅提高，各层平均附加有效阻尼比如图7（b）所示，层间位移角显著减小且沿结构高度方向分布更均匀，提取三轮设计中RSN1486 波下10～20 s 间第2 层层间位移和附加有效阻尼比时程如图8 和图9所示，可见设计后的结构层间位移明显衰减，附加有效阻尼比显著提高，设计效果明显。通过算例分析，可见本文提出的双目标设计方法是合理可行的。

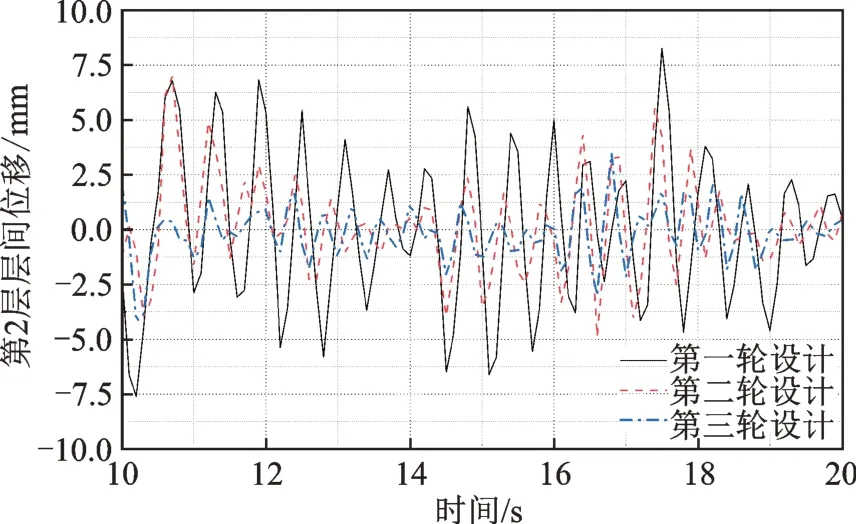
图8 第2 层层间位移时程Fig.8 Story drift time history of the second story

需要指出的是，本文设计变量为BRB 弹性刚度，也可以通过调整BRB 的屈服位移或数量来调整各楼层BRB 出力，即设计变量不是唯一的，此处不做过多展示。另外，结构层间位移角等性能指标与主体结构的梁柱尺寸、配筋方案和空间布局等因素相关，本节中算例仅为简化展示方案，工程设计应根据结构实际情况制定阻尼器布置方案，本文附加有效阻尼比取阻尼比时程平均值属于偏于保守的设计方法，最终的动态附加有效阻尼比最大值已达到1.26%，如有需求也可采用最大值或其他统计值表征附加有效阻尼比，目标附加有效阻尼比和层间位移角限值同样应根据实际工程需求制定。

4 结论

针对目前减震结构传统附加阻尼比计算方法的局限性，本文推导了基于Bouc-Wen 模型显式解的滞回能量解析公式，进而建立了时变阻尼比计算方法，最终提出了面向阻尼比-位移双目标的减震体系设计方法和流程，结合算例对设计方法的可行性和先进性进行了验证。主要结论如下：

（1）应变能法是一种阻尼比的估算方法，计算精度较差，计算结果偏大，不利于结构安全，而模态阻尼耗能法物理意义明确，是一种精确计算方法，两者计算结果在时域上变化趋势是相同的。

（2）随着时间段Td增大，两种方法的平均值均缓慢增大，应变能法最大值下降，模态阻尼耗能法最大值下降过程中伴随局部上升。当时间段Td取值大于结构第一周期T1时，统计结构耗能更完整且充分，但Td过大则无法充分体现阻尼比时变特性，因此建议Td在1.0T1～1.8T1之间取值。

（3）模态阻尼耗能法的平均值与最大值相比受时间段Td影响更小，稳定性高，建议采用该方法的平均值表征阻尼器的减震效果。

（4）通过增大某楼层阻尼器屈服力或数量的方法可以提高该层阻尼器的附加有效阻尼比，降低层间位移角幅，且可实现量化评估，验证了本文提出的双目标设计方法的合理性与可行性。