基于EKF的初始状态自适应室内融合定位算法*

胡文强， 胡建鹏， 吴 飞， 陆雯霞

(上海工程技术大学 电子电气工程学院,上海 201620)

0 引 言

随着5G的商用落地，室内定位技术再次引起人们的广泛关注[1]。日益增长的生活与商业需求的位置服务刺激了室内定位系统和相关技术的快速发展。典型的室内定位技术包括Wi-Fi、蓝牙、射频识别(radio frequency identification,RFID)、超宽带等。Wi-Fi定位的网络覆盖广，可满足大多数室内定位需求，但其信号易受环境干扰，导致定位结果波动较大。行人航位推算(pedestrian dead reckoning,PDR)定位方法利用惯性传感单元(inertial measurement unit，IMU)实现航位推算定位，目前移动终端设备支持良好，但存在较大的惯性累积误差[2]。

为提高上述单一定位系统的性能，研究人员对有关Wi-Fi与PDR的融合定位系统与技术进行了探讨与分析。文献[3]中Wi-Fi定位采用了一种改进的WKNN算法，PDR定位算法使用了多重约束条件的步态检测和在线步长估计方法，最后将扩展卡尔曼滤波(EKF)作为Wi-Fi和PDR定位的融合滤波器。文献[4]提出了一种鲁棒约束性的卡尔曼滤波(KF)来增强基于位置服务的性能并用于Wi-Fi/PDR组合导航算法。文献[5]采用的是一种基于最小二乘法的实时测距误差补偿模型和基于加权最小二乘法的自适应Wi-Fi精细时间测量定位算法，并利用紧耦合融合定位算法进行融合。文献[6]提出了一种基于自适应粒子滤波的室内行人Wi-Fi与PDR 组合定位算法，通过自适应因子自动调节观测量对粒子分布的影响。文献[7]在Wi-Fi定位上将空间搜索限制与均值滤波相结合来提高计算效率和定位性能，PDR部分提出了一种带有相关处理和测量噪声姿态确定的EKF算法以获取长期航向，并将一种自修正KF融合定位算法运用到Wi-Fi/MEMS融合阶段。

上述研究通过融合方法仍存在如下问题：1)忽略了包括始发位置与初始航向角在内的初始状态确定过程，这样可能会导致定位系统在有限时间内无法快速收敛；2)在使用EKF算法进行融合时，Wi-Fi数据的误差衡量往往使用了自定义的固定值，没有很好的将真实环境下Wi-Fi数据波动所带来的影响反馈给EKF系统。为此，本文在基于EKF的室内Wi-Fi/PDR融合定位算法基础上，提出了一种初始状态自适应的解算方法和一种基于邻近状态RSSI欧氏距离的改进EKF算法，降低了因初始值设定不当而导致的误差，同时能够根据定位环境与迭代所反馈的信息进行动态调整，从而提高了最终的定位精度。

1 单定位系统方法

1.1 基于WKNN的Wi-Fi指纹定位

Wi-Fi指纹定位包括两个阶段：采集指纹库的离线阶段和匹配定位的在线阶段[8]。

离线阶段通过移动终端收集特定Wi-Fi的信号强度数据，首先将待测区域划分为几个网格，用每个网格的顶点作为参考点(reference point，RP)；将每个RP经过优化后的特征信息(包括坐标信息、Wi-Fi信号强度值等)作为一组位置指纹数据[9]。

在线阶段利用接收到的信号强度数据通过匹配算法得到当前移动终端的位置。在线阶段使用WKNN算法，WKNN通过不同指纹节点的贡献比来给每个指纹分配权重，提高了KNN的算法精度[8]。未知点的估算坐标为

(1)

式中x,y为RP的坐标，wi为第i个样本点的权值。

1.2 PDR定位

PDR定位算法根据行人状态(位置、航向角等)的变化，实时累积计算行人的位置[10]。PDR的定位过程为：二维平面内，行人的运动轨迹可以通过步长和方向角计算得到，若已知tk-1时刻的位置坐标为Ptk-1=(Etk-1,Ntk-1)，则tk时刻位置坐标为

(2)

式中dtk-1为tk-1时刻到tk时刻之间的行走步长，θtk-1为tk-1时刻的航向角。通过式(2)可以推算出每一步的状态信息。

在步频检测上，PDR可采用峰值检测法，通过检测加速度计输出信号的波峰来识别行人步数，对两个连续波峰的搜索即确定为一步[11]。而在步长推算上，本文通过Weinberg步长估计模型来推算行人步长

(3)

式中k为步长比例因子，amax和amin分别为行人行走一步时所检测到的最大加速度和最小加速度。

2 基于EKF的Wi-Fi/PDR融合定位算法

在EKF融合定位系统中，本文在初值确定上采用了初始多点协同卡尔曼滤波的方法，融合系统在EKF的迭代过程中对相邻两个状态的RSSI欧氏距离进行度量，并反馈给EKF系统的下一状态，从而降低了Wi-Fi数据波动对系统所造成的影响，获得了精确而又稳定的融合定位结果，本文的系统流程如图1所示。

图1 Wi-Fi/PDR融合定位算法流程

2.1 初始状态的解算

KF初值偏差可能会导致滤波计算的前若干步结果产生较大偏差，即使进入收敛状态后，也可能因为初值设置不当，导致结果不能收敛到状态的真实值。因此，本文采用了基于KF的初始位置和多点KF的航向角解算方法。

通过对KF公式的迭代推导[12]，可得第k次的迭代结果为

(4)

假设可以获取初始m个定位点，其中,第i个定位点的Wi-Fi扫描次数为ki，则可以得到滤波后的定位点Li为

(5)

其中,初始位置为L0，而初始航向角为θ0

(6)

2.2 基于相邻状态RSSI距离反馈的EKF算法

由于EKF算法的初始协方差矩阵为自定义常量，但复杂环境下的动态系统，其协方差矩阵不会为固定值，这里采用了以相邻状态下的RSSI欧氏距离为基础的噪声反馈机制[13]。

行人行走过程中，对相邻两步的RSSI信号指纹进行欧氏距离的求解，在每个系统中，它会保持在稳定的取值范围里面，记为[Dmin,Dmax]，然后将其线性放缩到了一个定位精度的阈值范围，即[Smin,Smax]，最后将其动态作为EKF的观测协方差矩阵的参数，以此来动态衡量Wi-Fi的噪声。

通过上一步的距离差决定下一步的观测协方差矩阵的协方差值，如式(7)所示

(7)

式中Dk为未知点与第k个状态的RSSI与上一个状态的欧氏距离。

通过多组实验测量可以得到在一个固定环境下Dk的取值范围为[Dmin,Dmax]，而该系统的定位精度范围为[Smin,Smax]，对其进行尺度缩放，则有

(8)

EKF的具体过程如下所示:

系统状态方程、观测方程分别为

(9)

(10)

由Wi-Fi指纹定位给出融合系统的初始位置(x1,y1)，初始协方差矩阵为P1，系统过程噪声协方差矩阵Q由行人航位推算方法各要素的平均误差组成，观测噪声协方差矩阵由Wi-Fi指纹定位的平均误差组成。融合定位系统状态值如下

(11)

(12)

EKF线性化与初始化完成后，滤波主要过程如下所示

X′k=AXk-1

(13)

P′k=APk-1AT+Q

(14)

Kk=P′kHT(HP′kHT+R)-1

(15)

Xk=X′k+Kk(Zk-HX′k)

(16)

Pk=(1-KkH)P′k

(17)

3 算法验证与分析

本文选取某校电子电气工程学院大楼7楼作为实验场所，在地面标定1 m×1 m方格，并以其顶点作为实验样本采集点，如图2所示。实验选取了8个TP-LINK型号为TL—WR886N的路由器作为定位信标，采用华为荣耀8作为PDR和Wi-Fi数据的采集工具，分别采用Wi-Fi定位、PDR定位和基于EKF的Wi-Fi/PDR融合定位算法进行定位实验。实验的行走轨迹为L型路线，起始坐标为(2,1)，终点坐标为(14,13)，总共行走步伐为30步，总计31个位置状态，实验采用了固定步长的行走方式，每一步的距离为0.8 m。

图2 实验场景

3.1 初始状态的分析实验

对于初始位置，在初始航向角已知的情况下(设为0°)，以1 m为间隔，将初始位置偏差值设置为1～10 m，对于其中1，5，10 m轨迹的偏移情况如图3(a)所示。由输出的轨迹图可见，虽然在开始时会有较大的偏离，但最后都能收敛到正常值附近。往往位置偏差的距离越大，收敛的迭代次数也会越大，但是偏差超过一定界限以后，收敛次数会相对稳定下来，如表1所示。

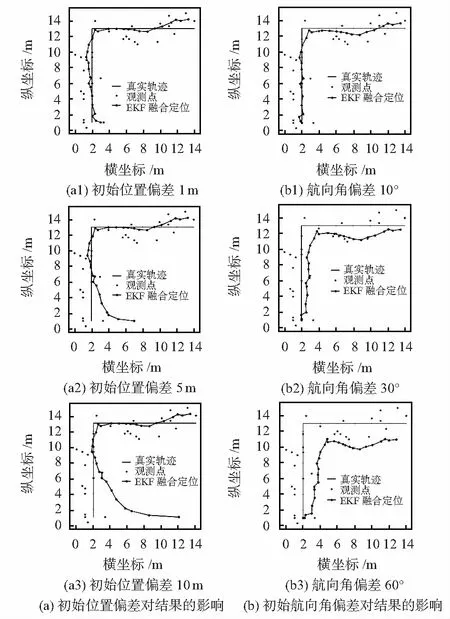
图3 位置与航向角偏差对结果的影响

表1 位置偏差与其对应的收敛迭代次数

对于初始航向角，在初始位置已知的情况下(设为(2,1))，以5°为间隔，将初始角度偏差值设置为10°～60°，对于其中10°，30°，60°轨迹偏移情况如图3(b)所示。通过输出的轨迹图可见，初始航向角的偏差不会影响输出结果的收敛速度，但结果会产生持续的偏差，偏差结果会以较慢的速度向正常值附近逼近，所以可以通过平均定位误差来衡量航向角偏差对结果造成的影响，如表2所示。通过数据可以发现，航向角偏差越大，平均误差也会越大，当前实验数据的Wi-Fi定位精度为1.92 m，而在航向角偏差达到45°时，30步迭代后的误差值为1.99 m，此时融合定位的系统误差大于单个系统的误差。

表2 航向角偏差及其对应的平均误差

通过对以上数据的分析，可以得出：通过EKF对Wi-Fi与PDR进行融合定位时，需要满足以下条件可以视为一组可接受的初始状态

Δs≤3m and Δθ≤40°

(18)

如果EKF融合定位系统比单一系统至少要提高30 %的精确度，并以此视为一组良好的初始状态，则需要满足以下条件

Δs≤3m and Δθ≤30°

(19)

3.2 初始状态的解算实验

实验分析了式(6)中m取值不同时初始状态的偏差情况，对5组实验数据进行求解得到表3的结果，初始位置的平均偏差为Δs=0.11 m，满足式(19)。航向角的偏差情况与其算法复杂度如图4所示，随着m增加，航向角初始状态越好，尽管随之复杂度也会增加，但m=5时算法耗时也在20 ms内，不会影响最终的用户体验。

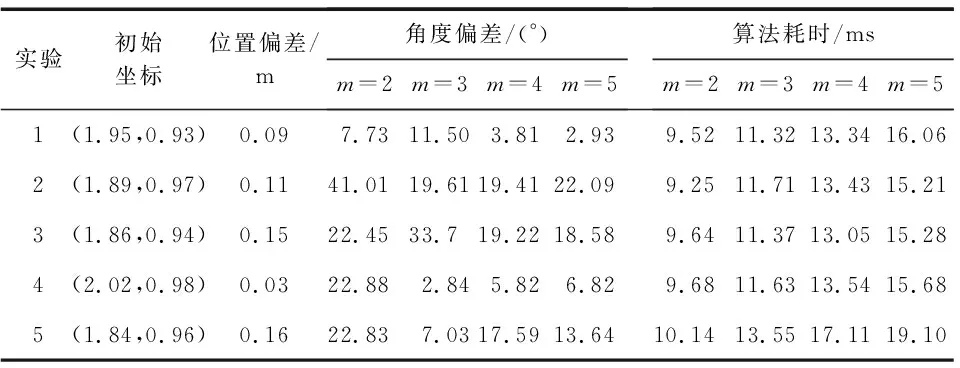
表3 初始状态解算实验结果

图4 不同m取值的算法解算结果

通过本文提出的初始状态解算方法，定位结果能够快速收敛，4步内即可达到收敛状态，输出图像逼近真实轨迹，如图5所示。

图5 多点协同KF的初始状态解算方法

3.3 改进的EKF算法

图6 定位轨迹对比

图7 定位误差对比

结果表明Wi-Fi定位虽然能够输出一个绝对定位值，但数据波动较大，其平均定位精度为1.92 m ，PDR定位在短时间内可以保持良好的精确度，但随着迭代次数的增加，累积误差会越来越大，在30步内其平均误差为1.19 m，但到达终点时误差为2.21 m。

4 结束语

本文提出的改进EKF算法能很好地融合了Wi-Fi与PDR的优势，其平均精度为0.97 m，相较于其他EKF算法，其精度有较为明显的改善，其输出结果比其他EKF算法平均精度的1.14 m改善了17.2 %，表明本文所提方法能够有效抑制误差，提高定位精度。