基于Spar平台结构参数量测的不确定度分析*

李 敏， 曹 乐， 黄经纬

(上海工程技术大学 电子电气工程学院，上海 201620)

0 引 言

Spar平台用于深海石油的钻探、生产、储存和卸载，一般包括上部模块和柱体模块两部分，可作业于水深400 m以上[1,2]。由于其自身具有深吃水和大惯性的优点，Spar平台在工作条件下不会引起较大的垂荡和纵摇运动。然而，当遇到长周期的涌浪或近共振周期时，仍会造成平台的失稳[3]。参数失稳是一种可能引起海洋结构物过度运动的现象[4]。Hong Y P等人[5]通过一系列的测试模型对Mathieu不稳定问题进行研究，提出当垂荡频率与纵摇固有频率相近或为其2倍时，会发生较大的参数纵摇。Jameel M等人[6]通过应用Spar平台的不稳定三维图，得到增加初稳性高可减小参数的失稳区域。同时，减小初稳性高的变化可进一步避免Spar平台陷入不稳定。桑松等人[7]通过采用理论分析与数值模拟相结合的方法，表明垂荡运动幅值的增大是Spar平台发生Mathieu U S不稳定现象的主要原因。Nallayarasu S等人[8]通过采用面板法对平台的水动力响应进行了数值模拟，研究结果表明，水线面面积的减小有利于增大垂荡运动的固有周期，从而增加Spar平台的稳定性。李伟等人[9]采用1︰120的Spar平台制作模型，在规则波中进行垂荡—横摇—纵摇耦合运动响应试验，指出当入射波浪频率在垂荡固有频率附近变化时，平台的运动响应幅度会发生跳跃现象。为了使Spar平台更加稳定，可参考Spar浮标的结构设计，即增大纵摇运动的固有频率，但尚未判断结构尺寸参数对纵摇运动固有频率不确定度的影响程度[10]。基于以上分析，目前大部分文献通过数值分析或实验验证的方法讨论了影响Spar平台稳性的敏感参数，并没有对这种影响进行量化分析。

为了解决上述问题，本文通过建立Spar平台垂荡—纵摇运动响应模型，考虑由建造过程中引起的结构尺寸的不确定性，并基于所选样本的随机模型分析了不确定的结构参数对Spar平台纵摇固有频率的影响，得到其中的关键因素，帮助设计人员在Spar平台的设计初期提供建议或优化参考。

1 模型建立

为了定性分析Spar平台结构参数对纵摇运动固有频率的影响，本文将Spar平台在运动过程中的排水体积、阻尼等因素作为一个常量。根据图1中所给Spar平台模型，忽略波浪力的影响，重点研究Spar平台在垂荡运动作用下引起的纵摇运动。首先，考虑Spar平台的纵摇运动特征，其微分方程[11]表示为

(1)

式中I55为纵摇运动的转动惯量，A55为纵摇运动的附加转动惯量，ξ5(t)为纵摇角，B55为阻尼系数，Δ为浮体排水量，dGM0为浮体在静水中的初稳性高。转动惯量与附加转动惯量表示如下

(2)

(3)

式中kyy为回转半径，l为平台长度，ρ为海水密度，D为平台直径，dKG为K与G的距离，Df为平台吃水深度。

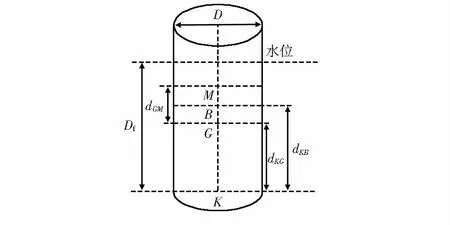
图1 Spar平台结构模型

另外，纵摇回复刚度K55的大小由浮体排水量Δ与浮体初稳性高dGM0的乘积决定。随着平台的运动，浮体初稳性高和瞬时排水量发生改变，即Spar平台在长周期浪涌情况下的纵摇运动回复力矩将发生变化。

垂荡位移ξ3(t)可以表示为

ξ3(t)=ξ3cos(ω3t)

(4)

式中ξ3(t)为垂荡位移，ξ3为其幅值大小，ω3为垂荡运动的频率。

初稳性高dGM表示为

(5)

式中η(xw,yw,t)为瞬时波面上升高度。

浮体排水量表示为

(6)

忽略高次谐波项，不计波面升高的影响，纵摇回复刚度表示为

(7)

将式(7)代入式(1)中，并对其进行无量纲化处理，纵摇运动方程可表示为

(8)

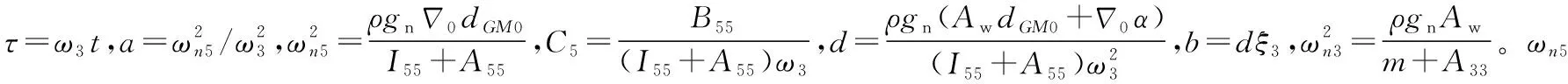
(9)

2 不确定度分析

基于Spar平台纵摇运动固有频率的确定性模型，根据输入参数的不确定性对输出参数进行量化分析。图2给出了基于样本随机建模的详细过程，输出参数的可变性是通过随机选择的许多不同输入参数组合进行评估，主要包括以下2个步骤：首先,根据输入参数的概率分布函数，通过收敛性分析量化输入参数的不确定性，当输入参数收敛于一个确定值时即可选定输入参数组合的数量；然后,利用已经建立的确定模型将输入参数的不确定性映射到输出参数上，并根据结果对输出参数的可变性进行量化。

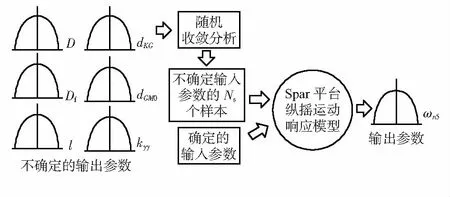
图2 基于样本的随机模型

根据输入参数的概率分布函数可表示其不确定性，并通过蒙特—卡洛采样方法生成参数的随机样本，基于该样本即可利用确定性模型对输出参数的不确定性进行分析。

Spar平台的动态响应主要取决于海浪运动及平台自身结构参数，由于海浪运动为不可控因素，本文仅考虑平台结构尺寸对其动态响应的影响。因此，本文根据输入参数平台直径D,排水深度Df,长度l,dKG,初稳性高dKG0及回转半径kyy的分布情况对输出参数纵摇运动固有频率ωn5及参数d的不确定度进行分析。由于以上输入参数为设计建造过程所确定，其不确定度可根据实际平台尺寸来设置。假设各输入参数对应的选值集合均满足均值为μ，标准差为σ的正态分布，本文将均值作为输入参数的设计值，标准差表示平台建造过程中的设计误差，输入参数的不确定度Cov定义为对应标准差与均值的比值，即Cov=σ/μ，显然，标准差越大、均值越小的输入参数的不确定度越大，而确定参数的不确定度为零。

通过对输入参数与输出参数进行随机收敛分析进一步确保所选样本具有代表性，从而确定样本个数。在随机收敛分析过程中，输入与输出参数的均值与方差均会随着样本数量的增加，收敛到相应的设计值与计算值，因此，可通过随机收敛分析的方法确定样本的个数Ns。参数样本选定后，将各个样本分别代入所建立的输入、输出参数的确定性模型中，从而获得输出参数的不确定性，进而评估可变输入参数对输出参数不确定度的影响。

由于输入参数具有可变性，通过确定性模型计算得到的输出参数才具有不确定性，本文定义四分位差IQR来量化输出参数的这种不确定性，该值代表输出参数分布中25%概率位置对应值P25与75%概率位置对应值P75的差值

IQR=P75-P25

(10)

3 收敛性分析

根据输入参数的概率分布函数可表示其不确定性，并通过相应的抽样方法生成参数的随机样本，基于该样本即可利用确定性模型对输出参数的不确定性进行分析。因此，本文根据输入参数平台直径D,排水深度Df,长度l,dKG,初稳性高dGM0及回转半径kyy的分布情况对输出参数纵摇运动固有频率ωn5的不确定度进行分析。为了使输出参数的分布更具代表性，需要大量输入参数样本对输出参数进行评估，由于该过程计算量较大，无法直接应用于实际操作中。因此，本文通过收敛分析方法确定能代表输入参数组合分布的最少样本数量，同时保证输出参数的稳定分布。

表1给出了一种经典Spar平台的主要参数，由于测量过程中存在误差，很难得到相关参数的准确值，因此将基于该平台设计值选定输入参数组合的样本数量：D=37.2 m,l=212.9 m,Df=198.1 m,kyy=59.2 m,dKG=89.0 m,dGM0=10.08 m，且将以上输入参数的不确定度Cov均设为0.01。

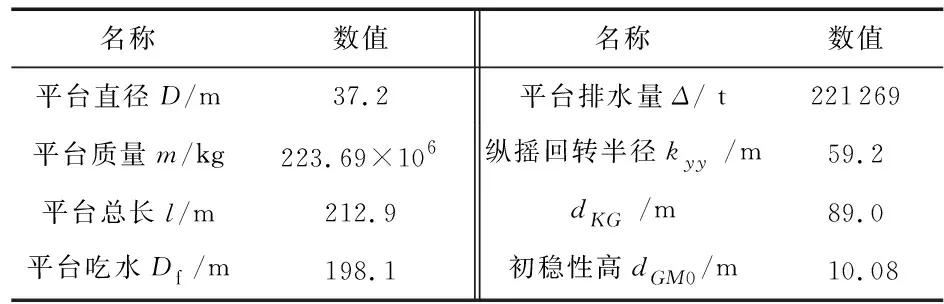
表1 Spar平台主体尺度参数

输入输出参数通过利用随机收敛方法对不同数量下的样本进行分析。输入参数的随机收敛分析如图3所示。

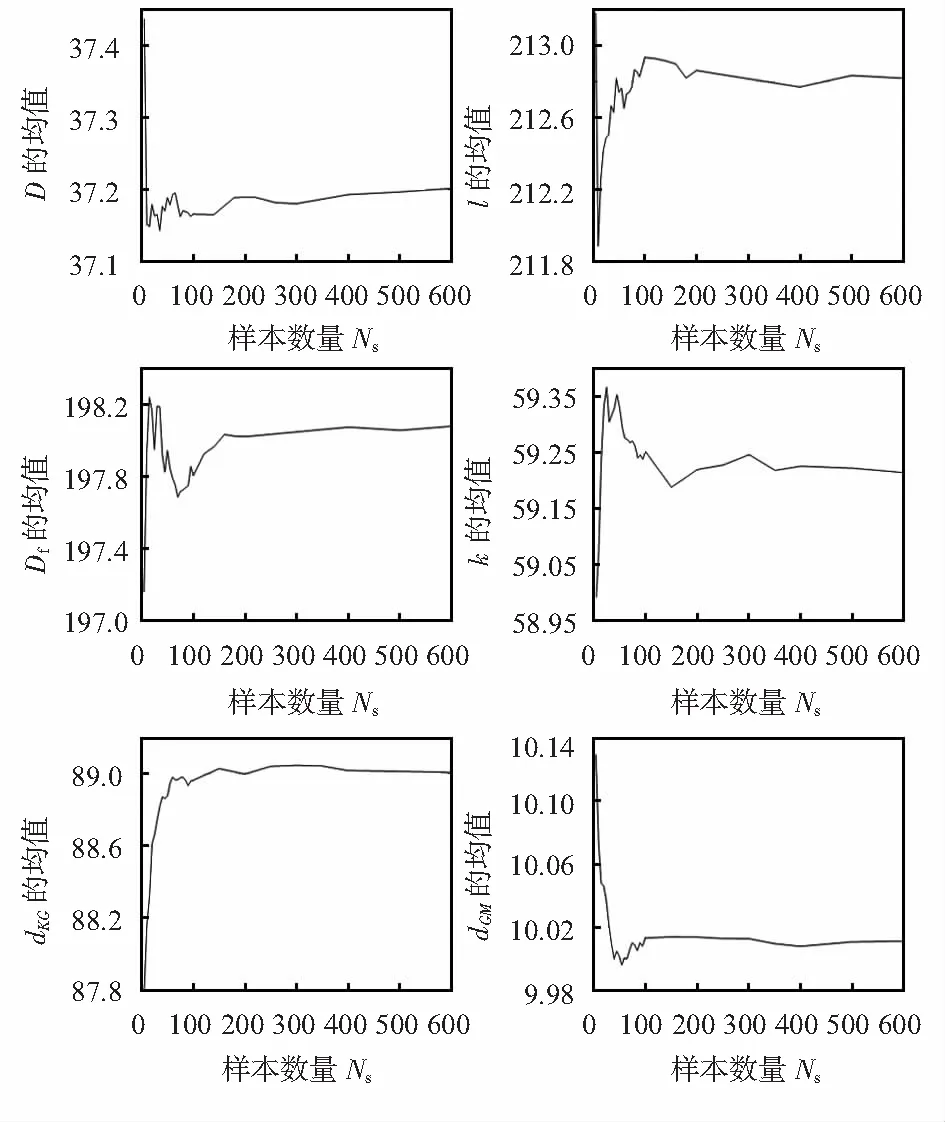
图3 输入参数的均值收敛分析

观察图3可发现，当输入参数的样本数量Ns<300时，输入参数的均值波动较大；当Ns=300时，输入参数虽仍有一定的波动，但波动范围均控制在1%以内。因此，300个样本可以保证输入参数的均值稳定地收敛至给定值。对于输入参数标准偏差的收敛分析如图4所示，由于标准差为均值的高阶函数，当输入参数样本数仍取300时，标准差并不会像均值呈现出很好的收敛态，波动依然很大。此时，必须增大样本数量以保证输出参数的稳定分布。当样本数量增大到500时，输入参数(D,l,Df,kyy,dKG,dGM0)的标准差分别在0.14%，2.28%，0.57%，1.8%，1.19%，0.99%，波动幅度均在2.5%以内。

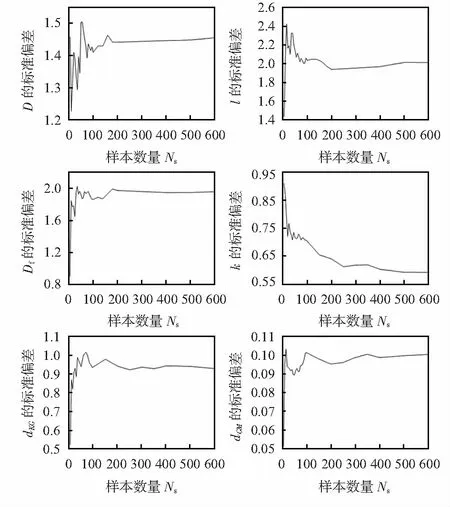
图4 输入参数的标准差收敛分析

同样，对确定模型下的输出参数进行收敛性分析。由图5很容易得到，当样本数量Ns=300时，输出参数的均值很容易收敛到给定值，该样本数量下完全满足输出参数的稳定分布。为了同时满足其标准差的波动幅度也收敛至较小范围内，如图5(b)所示，当样本数量增大至500时，输出参数的标准差波动幅度可收敛至4%以内，能够作为代表性样本。根据以上收敛性分析，选取样本个数Ns=500，能够进行后续分析。

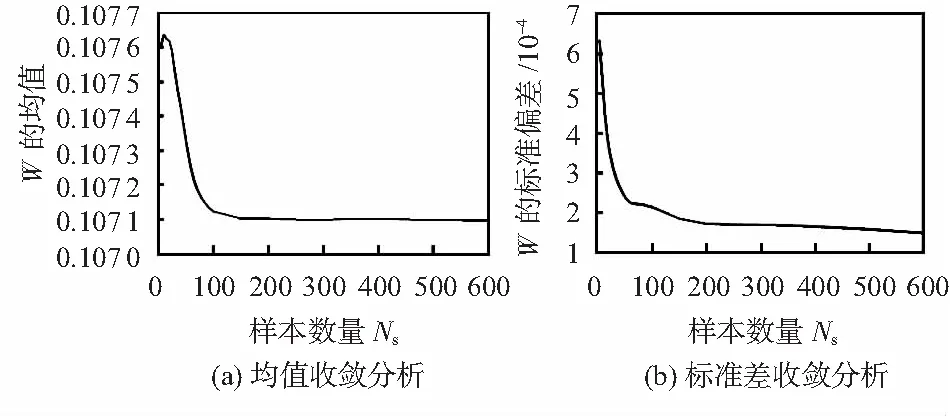
图5 输出参数的均值收敛与标准差收敛分析

4 输出参数不确定性分析

图6给出了输出参数的分布情况，显然，该分布已经不满足正态分布的定义，这是由于所构建的模型中含有非线性因素。其中，P5,P25,P50,P75分别为输出参数分布直方图中5%,25%,50%,75%概率位置对应值。由式(10)计算可知，输出参数ωn5的分布情况与IQR的大小一致。因此，可以用IQR来量化表征输出参数的不确定性。

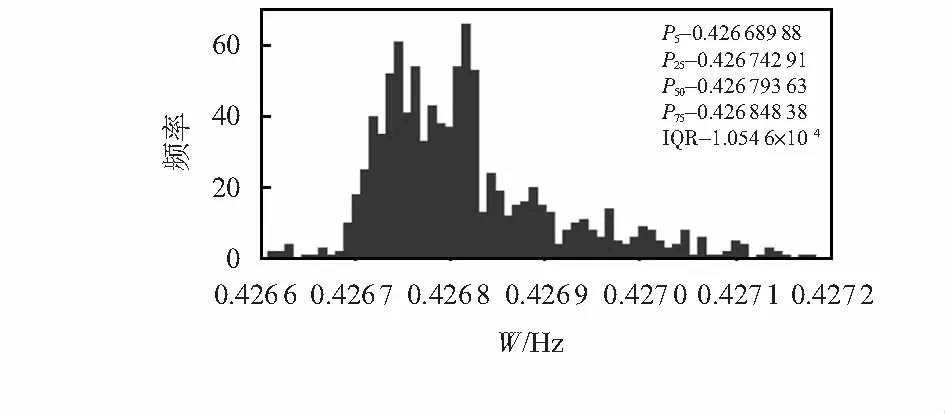
图6 输出参数ωn5的直方图分布

为了分析输入参数对输出参数不确定性的影响程度，可采用控制变量法将多变量问题转化为单变量问题，从而研究被改变的输入参数不确定度Cov对输出参数的影响。将变化的输入参数Cov的范围设定为0.01～0.11，其他输入参数的Cov均保持0.01，根据输出参数ωn5的IQR与输入参数D,Df,l,dKG,dGM0及kyyCov函数的对应关系，得到图7中不同输入参数的Cov对不同输出参数IQR的影响。观察图7输出参数ωn5的IQR的影响分布图，当平台直径D的Cov从0.01增大到0.11时，ωn5的IQR的变化范围最大，表明纵摇固有频率ωn5受平台直径D的影响最大。同时，改变平台初稳性高dGM0的Cov时，ωn5的IQR也会受到较大影响，当dGM0的Cov从0.07增长至0.09时，输出参数ωn5的IQR由0.000 197 8增长至0.000 397 1，继续增大Cov到0.11，此时输出参数IQR的增长速率达到1.45 %。其余输入参数Df,l,dKG和kyy对ωn5的IQR几乎没有影响。

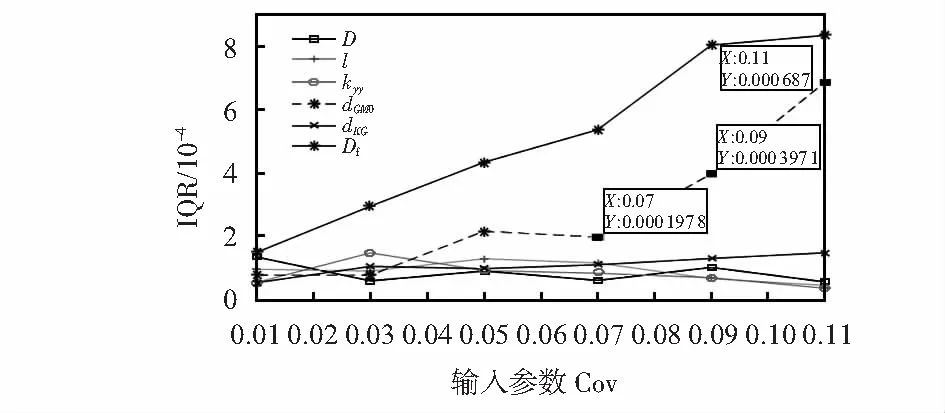
图7 不同输入参数Cov对应的ωn5的IQR

5 结 论

本文采用不确定度分析方法，建立了基于随机采样的不确定度分析模型，通过该模型评估了Spar平台直径、排水深度、平台长度、初稳性高及回转半径对纵摇固有频率的影响。研究表明:平台直径与初稳性高的改变对Spar平台纵摇固有频率的影响较大。鉴于以上建议，目前正在建造或直到今天建造的Spar平台被认为是相对良好的设计。对于不稳定的运动问题，这些Spar平台的典型特征可能没有大的问题。但是，当要进行新设计或修改现有的Spar设计时，本文介绍的结构参数的不稳定性分析方法和上述建议可以向设计人员提供参考。