基于轨道检测参数的高速列车车体振动预测方法*

卑王璐, 钟倩文, 郑树彬, 罗文成， 彭乐乐

(1.上海工程技术大学 城市轨道交通学院, 上海 201620；2.常州路航轨道交通科技有限公司，江苏 常州 213000)

0 引 言

中国轨道列车运行呈高速化与重载化发展趋势，由轨道磨损、不平顺等因素而引发的车辆振动愈发加剧[1]，强烈振动变化会影响列车运行舒适度。针对该问题，有必要对高速列车车体振动进行准确预测，但影响车体振动因素众多且其相互耦合关系复杂，所以如何利用好既有的轨检车检测轨道数据，建立快速预测评估模型，准确预测车体振动情况，对高速列车的稳定运营具有重要的意义。

徐磊、陈双喜、Li X等人建立传统车辆—轨道动力学模型[2～6]并施加轨道不平顺激励求得车体振动响应预测，但以经验轨道谱不平顺作为激励难以与现场实际应用达成一致。包学海等人依据多体动力学理论，郭训等人根据有限元分析理论，分别建立了几种车辆—无砟轨道—路基的耦合振动模型[7～9]，仿真出不同车速下或者轨道扣件不同工况下对车辆加速度的影响，但由于不同车辆建模参数各不相同，故只以车辆动力学建模预测振动，其精度难以保障。

机器学习的方法对列车振动分析具有高效率、高鲁棒性的特点。Qian K等人建立了基于神经网络和多体动力学模型的车辆振动加速度预测模型[10]。耿松建立了轨道不平顺状态下的神经网络车辆振动预测模型[11]。Xie J 等人用深度信念网络[12]对傅里叶变换处理后的振动信号进行特征提取训练。徐硕建立了基于PCA-SVM方法的车体振动状态分类预测模型[13]。而以上的机器学习预测方法都缺乏结合车辆动力学理论有效筛选振动相关检测参数的前提，对车体振动的预测准确性有限。

针对上述研究分析，本文一种提出利用实际轨道参数进行CART回归树预测振动的方法。首先,使用Simpack仿真建立了车体振动和轨道几何参数的联系，然后,根据GJ—5轨检车实测轨道几何参数，使用CART回归树建立了车体振动预测模型。将预测值同实际振动值进行实验验证，并就模型评价指标与BP神经网络、Interactions线性回归和线性支持向量机(support vector machine,SVM)进行比较，证明了本文预测方法的准确有效性。

1 CART回归树预测模型

回归树算法使用局部数据对周围复杂数据点进行建模从而简化建模复杂度。其通过决策点的建立来分割预测的相关数据，并使用回归算法对分割后的局部数据进行训练，相较于其他回归算法，回归树比较适合对复杂数据与非线性数据的建模[14]。

1.1 CART回归树生长

CART回归树构建原则是从根节点开始将样本集的属性与数特征节点比较，根据比较结果将样本集划分成不同的子节点。每个子节点再根据样本子集的值范围继续进行比较，直到叶节点为最终决策结果。其针对连续数据的分裂准则是回归方差[15]，选择回归方差最小的数据作为最优分裂点，最后预测结果就是所有叶节点的平均值。

将与车体振动相关的样本数据集划分为L个单元α1,α2,…,αL,且每个单元αl都有一个固定的输出振动加速度值Cl。故回归树模型可表示为

(1)

模型输出值与测量值之间的平均误差为

(2)

根据分裂原则，平均误差在Cl为所有实际车体振动值的平均值时达到了最优

Cl=ave(yi|xi∈αl)

(3)

1)最优切分变量和最优切分点的寻找

假设数据集第i个变量x(i)作为切分变量和其取值s为切分点，则该数据集可定义为2个区域

α1(i,s)={x|x(i)≤s},α2(i,j)={x|x(i)>s}

(4)

为寻找最优的i和s，定义c1,c2为区间的均值并求解如下

(5)

2)回归树归纳算法

将数据集经过式(4)～式(5)求解出最优解(i,s)，以此划分区域并在各自子区间中确定区间的输出值

α1(j,s)={x|x(j)≤s},α2(j,s)={x|x(j)>s}

(6)

(7)

根据上述步骤递归地对划分出的2个子空间，继续进行划分，直至节点变为纯性节点。最终，将输入空间划分为L个区域形成决策树为

(8)

1.2 CART回归树剪枝

为防止CART决策树的建树过程中出现过拟合现象，利用使用k折交叉验证法[16]，来测试回归树生长产生的子样本分支是否需要修剪。首先，将数据集分为k组，以k-1组训练集使树生长，最后，用1组验证集测试其分支规则是否重现并决定剪枝。重复k遍模型验证遍历，并最终平均k组预测值得到最终估计预测值。

1.3 模型评价指标

为更直观地描述模型预测效果，采用拟合度(R-squared)、平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)等模型评价指标对预测算法进行评价。公式如下

(9)

(10)

(11)

2 实验数据获取

2018年，GJ—5轨检车在广深Ⅱ线采集了37种参数，为筛选其中与车体振动强相关参数，本文使用SIMPACK建立车辆动力学模型，以轨道激励的形式仿真车体振动同轨道不平顺的关系，从中筛选出预测模型样本数据集。

2.1 车辆动力学建模

本文通过SIMPACK建立了高速车辆动力学模型[17]，简化车辆系统为车体、构架和轮对等为7个刚体，各构件自质心左右、前后对称等。建模过程中将轨道状态视为激励源，以施加轨道谱激励的形式，通过车轮向系统输入。车辆模型重要参数如表1所示，车辆简化动力学模型如图1所示。

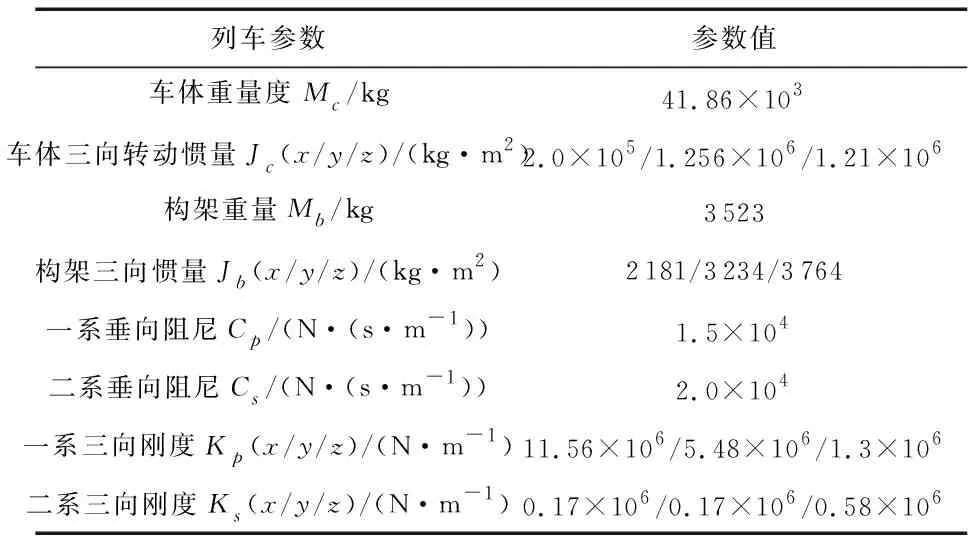
表1 车辆模型重要参数

图1 车辆简化动力学模型

2.2 车体振动仿真分析

由于中国尚未建立统一轨道功率谱标准，因此，为分析轨道不平顺对车体振动的影响，选取常用的德国高速轨道谱[18]激励输入所建立的模型，分别更改其中的3种不平顺谱为低速谱值，对比其输出的车体振动变化如图2～图4所示。

图2为横向不平顺谱值更改时的仿真车体振动特性图。可知横向不平顺的变化，大幅度会影响车体横向振动，其余2个方向振动几乎无影响。

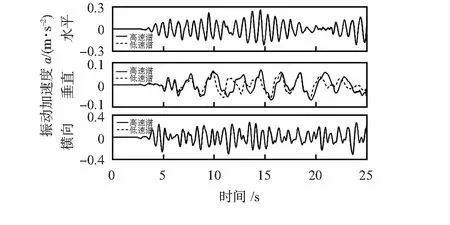
图2 横向不平顺车体振动对比

图3为垂向不平顺谱值更改时的仿真车体振动特性图。可知垂向不平顺的变化，对车体水平和垂向振动有较多影响，对横向振动几乎没有影响。

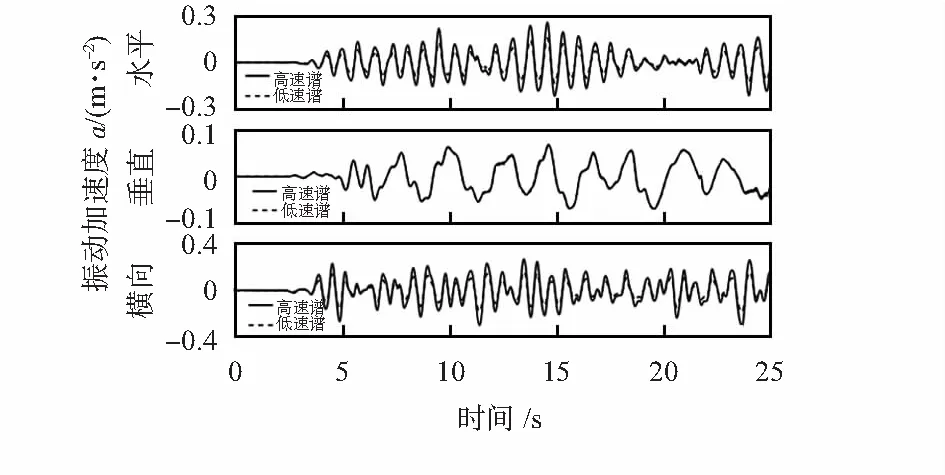
图3 垂向不平顺车体振动对比

图4为水平及轨距不平顺谱值更改时的仿真车体振动特性图。可知水平及轨距不平顺的变化，对三向车体振动均有一定且较大的影响。

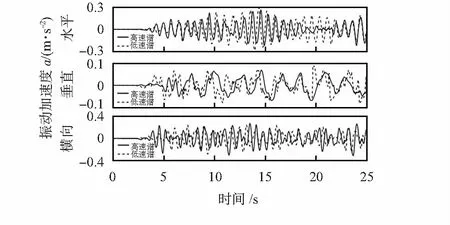
图4 水平及轨距不平顺车体振动对比

综上所述可知，轨道不平顺功率谱对车辆三向振动都有较大的影响。而轨道不平顺实际就是由对线路实际测量尺寸的随机波样本，从空域、时域、幅值域等方面的描述。以此为依据，从既有轨检车检测参数中筛选轨道几何检测类共30种检测参数，作为机器学习预测模型的样本数据集，如图5所示。

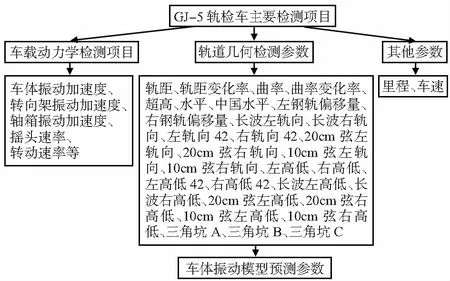
图5 GJ—5轨检车检测内容

3 实验与分析

视GJ—5轨检车采集的轨道几何检测参数为训练集，使用CART回归树算法并采用10折交叉验证进行树剪枝，设置该算法模型的最小叶节点样本数为12，建立了CART回归树的车体振动预测模型。并以同样的训练集，分别训练并建立BP神经网络模型、Interactions线性回归模型和线性SVM模型，同本文模型的评价指标进行对比如表2～表4所示。

表2 车体水平振动预测模型评价指标

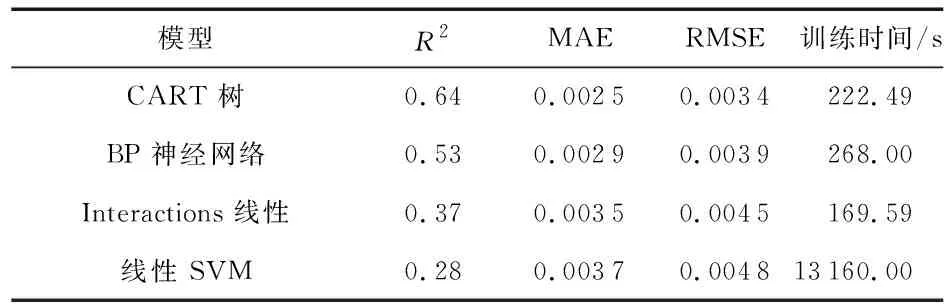
表3 车体垂直振动预测模型评价指标

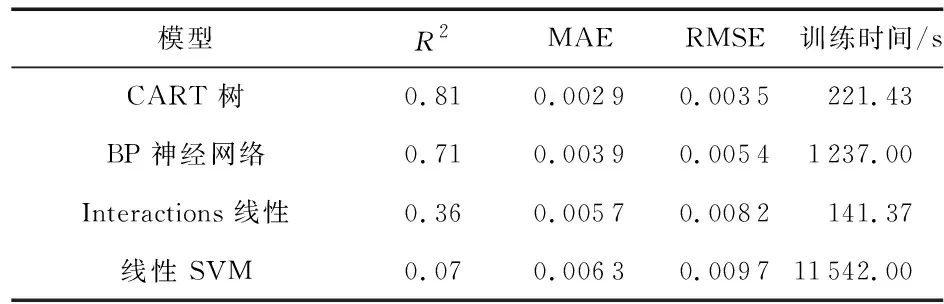
表4 车体横向振动预测模型评价指标

由表2～表4可看出：在3个方向的车体振动预测中，CART回归树预测模型的拟合度都最高，误差值都最低。该预测模型的拟合度水平方向可达0.88，MAE最小误差达0.002 5，RMSE最小误差达0.003 4，且模型预测时间较短。证明采用CART回归树算法在预测精度方面是一种较好的能够反映车体振动情况的方法。

此外将CART回归树模型预测的车体三向振动加速度与该线路高速列车100 km/h状况下实际振动加速度对比如图6所示。从图6中可直观地看出：CART回归树预测的车体三向振动值整体变化趋势与实际值保持一致，能够较好地反映车体振动情况。仅在加速度振动趋势突变处有一定偏差，其原因可能是由于样本数据集缺乏超限情况而造成的，此数据取自轨检车实测轨道几何参数，因此,需在实验室进一步补充各种超限工况进行改进与完善。

4 结 论

针对有效预测高速列车车体振动的问题，提出一种基于轨道几何检测参数的CART回归树车体振动预测方法。使用Simpack仿真建立了车体振动和轨道几何参数的关系，然后筛选GJ—5轨检车实测轨道几何参数作为样本数据，利用CART回归树算法，训练数据集并构建了车体振动预测模型。同其他预测模型对比，CART回归树预测模型在精确度和训练时间上有一定优势，对车体振动预测及保证列车乘坐舒适度具有重要参考意义。下一步将考虑优化模型精确度并增加超限工况数据进行更为准确的预测。