基于地磁匹配技术的室内定位系统设计*

孙建港， 周诗超， 刘 威， 温 鹏， 李 凯

(中北大学 信息与通信工程学院，山西 太原 030051)

0 引 言

在卫星信号可达的室外环境，全球定位系统(global positioning system，GPS)可以满足人们对室外精确定位的需求，然而GPS信号受建筑物遮挡和多径效应的影响，在室内环境下的卫星信号强度明显减弱，难以为室内人员提供准确定位服务。针对室内环境高精度定位需求，研究人员提出了基于几何关系原理的定位技术，例如WiFi[1]、无线超宽带(ultra-wideband，UWB)[2]脉冲、超声波[3]、伪卫星[4]、5G[5]等。该类型定位在无电磁干扰及视距等较为严格[6]的环境下通过计算发射端与接收端之间的时间差来确定位置信息，具有较高的定位精度；基于增量估计原理的定位技术，例如惯性导航[7]、视觉里程计导航[8]等，该类型定位在光线变化较弱、不考虑累积误差的条件下通过积分、匹配等方式测量前后历元间的位置、姿态变化来获取当前位置，具有精度高、可扩展性强的特点；基于指纹匹配的定位技术，例如信道状态信息(channel state information，CSI)[9]、磁场[10]等，该类型定位将待定位点的磁场数据指纹与定位区域的指纹特征进行对比，选择合适的匹配方法确定目标位置，一般不受时间和遮挡物影响，可以很大程度上降低定位系统的投入成本，为减少静态室内环境中的定位误差提供了方向。

在办公区域、医院隔离防护等复杂室内环境中，由于建筑钢筋水泥和铁质管道环境等因素的影响使得室内环境的地磁指纹信号源差异性较大，磁场信号适合作为位置指纹进行定位。以地磁信息为基础的室内定位技术作为一种无长期积分误差，不易被干扰的自主导航方式，在可用性、抗干扰性、自主性方面具有的天然优势。常用的地磁定位匹配算法主要有两大类，一类是相似度度量算法[11]，例如平均绝对偏差(mean absolute deviation,MAD)算法、均方差(mean square deviation,MSD)算法、绝对误差和(sum of absolute difference,SAD)算法等；另一类是基于迭代最近点算法的扩展[12]，例如迭代最近等值线点(iterated closest contour point,ICCP)匹配、迭代最近双等值点(double ICCP,DICCP)匹配算法等。

为满足室内复杂环境的定位需求，本文设计了以目标区域的三轴磁场数据为基础，利用小波分析与Kalman滤波相结合的方式对磁场数据进行优化处理，采用SAD算法对运动路径磁测序列进行匹配的室内定位系统。

1 室内定位系统设计

基于地磁匹配技术的室内定位系统，根据匹配特征量采集预先规划的定位区域所拥有的三轴地磁场数据，计算各点的地理坐标、三轴磁场强度的均值及方差，绘制能够反映地磁场分布情况的地磁基准图。当物体在定位区域内运动时，磁阻传感器实时记录运动路径的磁场数据，构成实际磁测序列，将磁测序列与地磁基准图数据进行算法匹配，搜索得到满足匹配条件的基准点，将基准点按时间顺序依次连接，从而得到物体运动轨迹，实现室内定位功能。

室内定位系统包含两部分，即硬件部分和软件部分。硬件部分包括地磁基准数据采集模块、传感器运动数据采集模块、无线传输模块；软件部分包括数据预处理模块、地磁基准图构建模块、地磁匹配模块。

室内匹配定位分为3个阶段。第一阶段为线下训练过程，使用地磁基准数据采集模块采集目标区域的地磁场数据，通过无线传输模块将数据传输至上位机，数据预处理模块对磁场数据进行滤波降噪，经地磁基准图构建模块，建立准确的地磁基准图；第二阶段为在线匹配过程，通过传感器运动数据采集模块，采集运动路径磁场数据，得到磁测序列，经由上位机的数据预处理模块处理后，通过地磁匹配模块将磁测序列与地磁基准图数据库的数据进行判定、匹配，获得实时匹配定位点；第三阶段为定位信息输出过程，由上位机输出物体运动轨迹的位置信息。

2 磁场数据预处理

2.1 地磁数据校正

当数据模块不处于水平面时，首先,需要计算出水平姿态角，然后,将采集模块的测量值投影于水平坐标系，设传感器俯仰角为θ，横滚角为γ，则坐标转移矩阵为

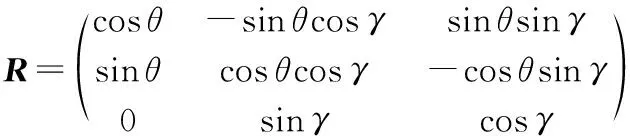
(1)

将传感器测量的磁场分量转移到地平坐标系内，则有

(2)

2.2 小波分析

设基本小波函数为ψ(t)，并对其进行伸缩和平移获得小波函数，其公式为

(3)

式中a为伸缩因子，b为平移因子。

X(t)的连续小波变换形式为

(4)

式中ψ′(t)为ψ(t)的共轭函数。

X(t)离散小波变换计算公式为

(5)

2.3 Kalman滤波算法

在所采地磁数据噪声满足高斯分布的情况下，可使用Kalman滤波对信号进行降噪处理。

状态更新方程为

X(k+1)=ΦX(k)+ΓW(k)

(6)

式中k为离散时间，系统在时刻k的状态为X(k)∈Rn；W(k)∈Rr为输入的白噪声；Γ为噪声驱动矩阵；Φ为状态转移矩阵。

状态更新的具体描述过程如式(7)所示

(7)

观测更新方程为

Y(k)=HX(k)+V(k)

(8)

式中Y(k)∈Rn为对应的观测信号；H为观测矩阵；V(k)∈Rr为观测噪声。

观测更新的具体描述过程如式(9)所示

(9)

上式用来计算对状态更新值的修正量，该修正量是由时间更新的质量优劣P(k+1|k)、观测信息的质量优劣R、观测与状态的关系H以及具体的观测信息Y(k)所确定。

2.4 小波与Kalman滤波融合

在采集过程噪声未知的情况下，Kalman滤波算法缺少计算必要的观测噪声方差R，本文采用小波分析对磁场数据进行分层处理，滤除原始信号的噪声得到小波去噪信号，再将原始信号与小波去噪信号进行做差处理，即可得到Kalman滤波所需的观测噪声估计值W(k)，根据噪声估计值可计算得到观测噪声方差值R。将估计噪声方差作为输入量进行Kalman滤波，重新对待处理磁场信号进行融合滤波处理。小波分析与Kalman融合滤波流程如图1所示。

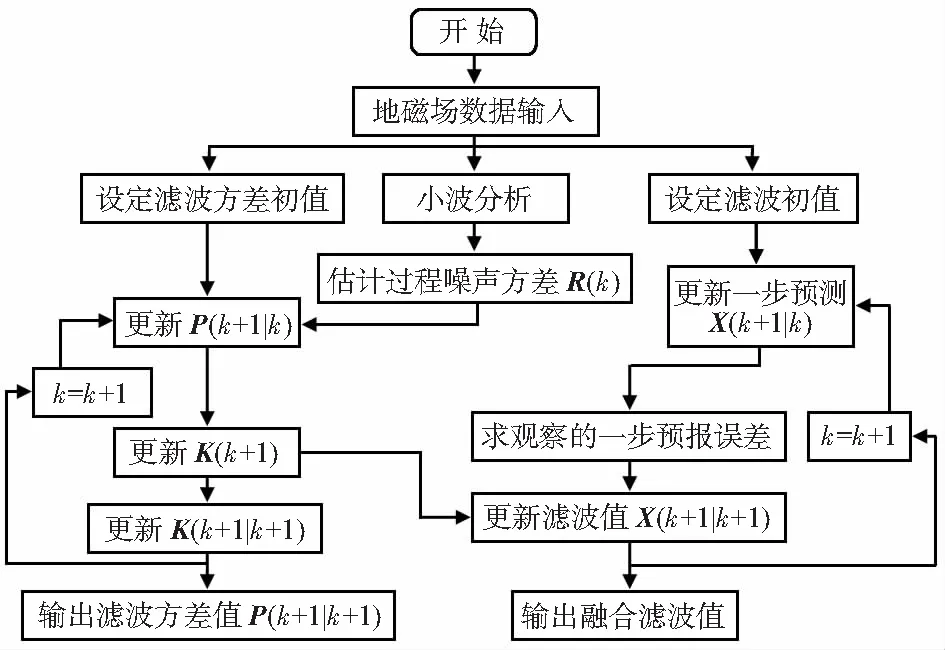
图1 小波与Kalman融合滤波流程

3 实验过程

3.1 地磁信息统计特性分析

不同的地理位置具有稳定且唯一的地磁数据特征，同一地点不同时间的磁场强度在某一区间内进行浮动变化，一般不超过10 μT，因此，可以将地磁场强度作为定位依据。利用地磁指纹图测量模块对目标区域进行多次测量，在各个定位点采集约15 s的三轴磁场数据，部分数据如图2所示。当处于静止状态采集基准点磁场数据时，信号较为平稳，当从一点移动至另一点时，运动时间间隔较短，采样频率较低，此过程采集到的磁场数据起伏较大，信号表现为尖峰、突变。采集到的同一点数据包含随机误差，放大观察可以发现采集过程中的磁场数据在一定范围内变化，其统计特性符合高斯分布。

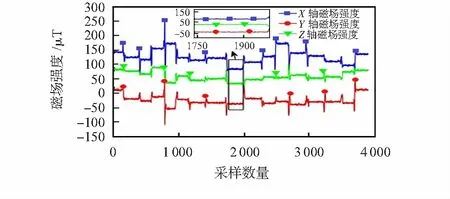
图2 三轴磁场数据

3.2 融合滤波

对已采磁场数据进行降噪处理，根据不同噪声频率采用小波进行多层分解，以X轴磁场分量数据为例，选择db5小波基函数进行5层分解，如图3(a)所示。将高频脉冲噪声、异常值进行分离，通过将原始信号与小波去噪后的信号做差，可得到小波分析滤除的估计噪声值，根据估计噪声值计算Kalman融合滤波的过程噪声方差。由于已验证磁场数据统计特性符合高斯分布，现结合Kalman滤波对地磁数据进行滤波处理，对于状态方程、观测方程进行定量分析。

由于状态量和观测量均为三轴磁场分量，则观测矩阵H为1；磁场强度在某一区间内变化微弱，则状态转移矩阵Φ可看作1。V=[v1,v2,…,vn]为未知的系统观测噪声，其方差式采集过程中的噪声信号方差，即小波分离的噪声信号，将所采磁场数据分量X=[x1,x2,…,xn]代入更新方程，最终得到Kalman与小波融合滤波后的磁场分量数据，结果如图3(b)所示。

图3 数据融合

3.3 构建地磁基准

本文所测地磁数据是在没有障碍物的区域内进行测量，但室内环境中有很多盲区无法进行测量，因此选择插值方式构建地磁基准图。选择面积约为100 m2的不规则展区作为实验场地，场地内陈列多种仪器设备，能够代表普通室内环境用于地磁匹配定位场景。使用地磁基准数据采集模块每间隔60 cm采集三轴磁场数据，每个基准点采集时长不低于15 s，采样频率为200 Hz，通过求取平均值获取基准点的磁场强度数据，共计452基准点。运用等值线的形式来图像化描述地磁场模型，不同插值方式的效果如图4所示，可以看出,地磁场数据的分布情况和变化规律。

依据表1可以看出，在数据的定量分析结合实际效果来看，克里金插值法最为合适。

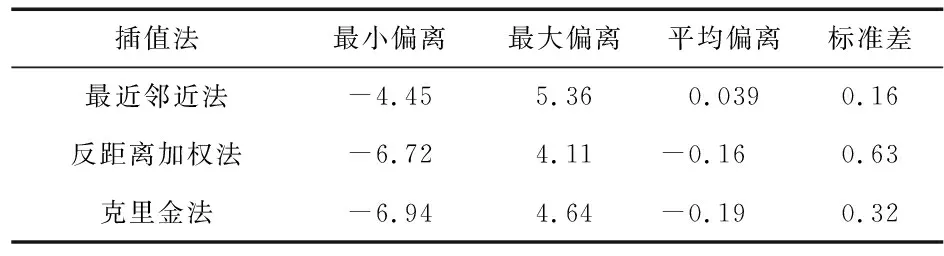
表1 常见插值方法指标比对 μT

选择克里金插值法将原始网格数据进行精细化处理，对数据进行密集网格插值，构建三维地磁基准图，网格交叉点为插值后的基准点。插值结果如图5所示。在后续定位过程中，将行走路径采集的磁场数据与地磁基准图数据进行比对分析，实现定位功能。

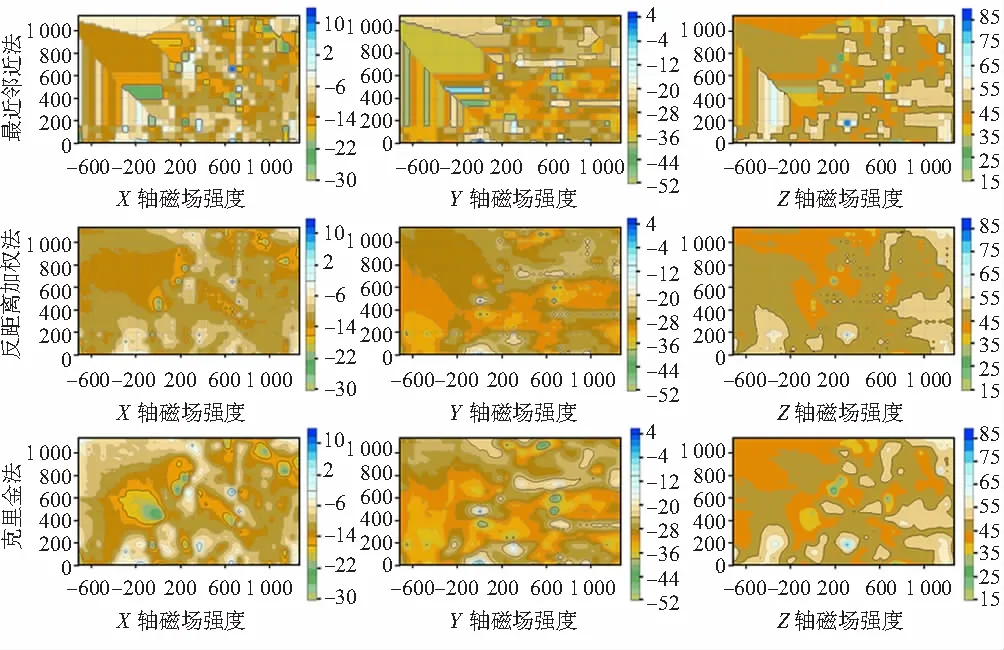
图4 等值线基准

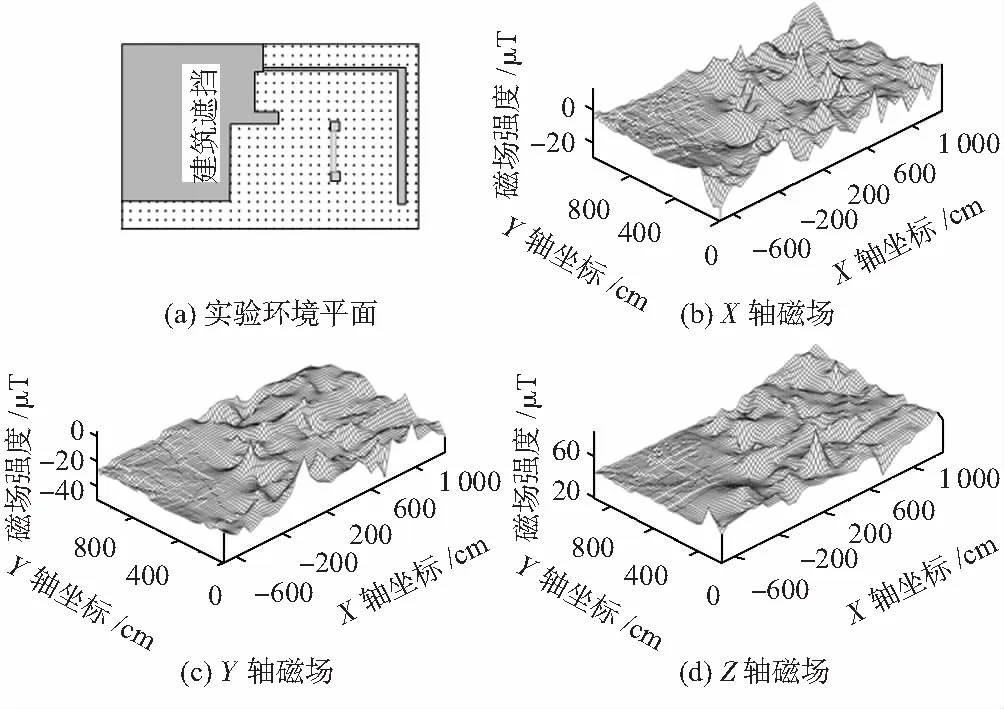
图5 三维地磁基准

4 实验验证

通过搭载MPU9250的传感器运动数据采集模块，对物体运动路线的磁场数据进行定点连续采集，同样经过数据预处理模块处理后，得到较为平稳的磁测序列，将磁测序列数据在地磁基准图中进行遍历、匹配得到符合匹配算法的运动路径基准点，连接各基准点得到传感器运动路径。

4.1 地磁匹配算法

本文选择使用基于相似度度量准测的SAD算法，其核心思想是将磁测序列中待匹配点与基准图的基准点对应数值之差进行绝对值求和，在遍历所有基准点之后，选择最小值作为最优匹配点[13]。

计算公式为

(10)

式中Csad为第i个基准图与待匹配磁测序列匹配点的绝对差值；Bi为地磁基准图的基准点；A为待匹配磁测序列匹配点；M,N为序列所对应坐标的行列数。

由于所采磁测序列为固定单点磁场数据集合，选择将处理后的磁场分量与三轴磁场基准图数据库数据进行做差进行绝对值求和，即为

Csad=|Bx(i)-Bx(A)|+|By(i)-By(A)|+

|Bz(i)-Bz(A)|

(11)

式中Bx(i)、By(i)、Bz(i)为磁场基准图中第i个基准点的三轴磁场强度值；Bx(A)、By(A)、Bz(A)为磁测序列中待匹配点的三轴磁场强度值，选择Csad最小值所对应基准点最为最优匹配点，最终将最优匹配点进行连接，对比理论路线进行定位误差分析。

4.2 路径磁场匹配

在已采地磁基准图信息的区域内做无规则运动，传感器经过19个基准点，每个基准点停留15 s，各个基准点之间的欧氏距离为1.2 m,1.8 m或2.4 m。将所采平稳点序列经降噪滤波处理后与理论路径基准点的磁场数据进行SAD算法匹配，磁测路径为实际运动路线，理论路径为预设轨迹，可作为先验信息可计算实际磁测路径的定位误差。如图6(b)所示，将磁测路径坐标与理论路径坐标对比发现2个坐标匹配点出现匹配异常，定位误差分别为0.6 m和1.34 m，匹配准确度约89 %。通过定位点磁场数据进行分析，两点地理位置较近使得部分磁场数据的空间差异性较弱，从而出现错误匹配。

图6 匹配定位

5 结束语

面对当前高精度的室内定位导航需求，设计了基于地磁匹配技术的室内地磁匹配系统，采集室内约100 m2的无规则区域的地磁场数据，通过小波变换分解磁场信号得到估计噪声，结合Kalman滤波对磁场数据进行降噪处理，分析对比不同插值方法，选择克里金插值法构建地磁基准图，使用SAM算法对定位区域内运动采集得到的19个磁测序列进行匹配，最大定位误差为1.34 m，平均精度为0.93 m，匹配准确率约为89 %，其结果表明，该系统可满足室内定位基本需求。