基于改进猴群算法优化ADRC的PMSM矢量控制策略*

易灵芝， 王艺皓， 李 旺， 陈 章， 李进泽

(1.湘潭大学 自动化与电子信息学院,湖南 湘潭 411105；2.大功率交流传动电力机车系统集成国家重点实验室,湖南 株洲 412001； 3.中车株洲电机有限公司,湖南 株洲 412001)

0 引 言

永磁同步电机(permanent magnet synchronous motor，PMSM)广泛应用于电动汽车、航空航天、智能机器人等行业[1]。相较于三相异步电动机，有更高的功率因数和硬机械特性[2,3]。为提高PMSM控制性能，文献[4]利用CKMTOA-KELM最优回归模型对扩展状态观测器中扰动量进行预测，有效提高了电机抗干扰能力;文献[5]通过使用离散终端滑模控制律提高了永磁直线电机的位置跟踪性能;文献[6]设计了一种基于指数趋近律的滑模控制器，在PMSM启动时能较快达到预定转速;文献[7]使用重复控制的PMSM矢量控制方案，通过周期性地补偿误差，改善电机控制性能。针对比例—积分(proportional integral,PI)控制调速系统很难满足电机高精度控制问题[8]，学者韩京清保留了PI控制优点，提出了自抗扰控制(active disturbance rejection controll,ADRC)技术[9]。但由于跟踪微分器与非线性状态误差反馈率中的Fal(e,α,δ)函数存在拐点,导致ADRC输出信号抖动、抗扰动性较差。

综上所述，本文提出了一种基于改进的猴群算法(im-proved monkey algorithm，IMA)优化改进ADRC的PMSM控制策略。该策略有效减少ADRC控制器[10]对参数设置的依赖；通过构造出新型非线性函数，显著降低ADRC输出补偿时的信号抖动。

1 基于改进型ADRC的PMSM调速控制系统

1.1 ADRC原理

跟踪微分器能准确地提取出给定信号中的微分信号，进而消除系统的初始误差[11]。以二阶系统为例，其离散形式[12]为

(1)

式中v(t)为电机的参考转速，r为速度因子，h为采样步长，v1(k)为函数v(t)在kh时刻的值，h0为跟踪微分器的滤波因子。

扩展状态观测器能够将电机所受到的总扰动以一种新的状态变量的形式输出，并且可以对此状态变量进行实时观测。其表达式如下所示

(2)

非线性误差反馈律[13]表达式如下

(3)

式中 选择合适的β参数可得到系统精确的控制量u0，实现控制目标。

1.2 ADRC的改进原理

为避免ADRC控制系统出现抖振现象，需Fal(e,α,δ)函数在原点以及分段点处尽可能平滑。当e>0时，对Fal(e,α,δ)函数求导，得到该函数在变量大于0时的微分形式为

(4)

在分段点δ处Fal′(e,α,δ)的取值为

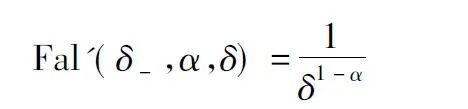
(5)

Fal′(δ+,α,δ)=αδα-1

(6)

当Fal(e,α,δ)在分段处可导时，存在Fal′(δ-,α,δ)=Fal′(δ+,α,δ)，此时α与δ需要满足

=αδα-1

(7)

求解后可得α=1，当α=1时，Fal函数将变为线性的恒值函数，不满足ADRC对最优控制函数非线性特性的需求。当α≠1时，将无法满足式(7)的要求。为此，本文提出在原有函数的基础上利用反正切函数、二次函数、三次函数以及差值拟合法构造出新型非线性Fal函数，构造思路如下：

新型控制函数在|e|>δ时表达式仍然为

nFal(e,α,δ)=sign(e)|e|α

(8)

当|e|≤δ时,新型控制函数的表达式为

nFal(e,α,δ)=a1·arctane+a2·e2+a3·e3

(9)

为保证函数在全部定义域内连续可导，需要满足如下条件

(10)

将式(8)、式(9)代入式(10)，得到式(10)中的系数为

(11)

将式(11)中系数代入式(9)中，即可确定新构造的最优控制函数表达式。

1.3 基于改进型ADRC的PMSM调速控制系统原理

对PMSM数学模型进行推导

(12)

为得到系统控制量以及扰动量信息，对式(12)进行进一步等效变换

(13)

式中f(t)为系统不可观测扰动。

基于改进ADRC控制器的PMSM控制调速系统如图1所示。

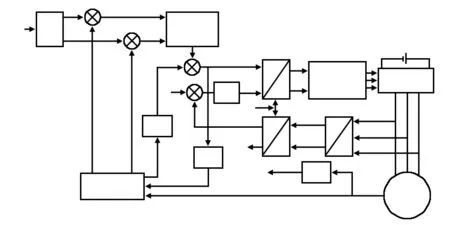
图1 基于改进型ADRC控制器的PMSM调速系统框图

2 IMA优化改进型ADRC的PMSM控制系统

2.1 猴群算法原理

猴群算法(monkey algorithm,MA)通过模拟猴群的“攀爬”、“观跳”、“空翻”等动作抽象出算法寻优步骤[14,15]。

攀爬过程：MA通过“伪梯度”的操作来实现该步骤。猴群中第i只猴子的位置为攀爬步长为为随机向量，向量中元素的产生规则为

(14)

式中R为介于0～1的随机数。Xi所对应适应度函数的伪梯度函数值f′i(Xi)为

(15)

式中f′ij(Xi)为目标函数值。通过伪梯度函数值可得到候选解位置

(16)

观跳过程：当观跳视野长度为s2时，可基于旧解Xi与视野长度s2产生候选解，产生规则为

(17)

空翻过程：空翻过程决定MA算法的搜索范围，空翻过程的候选解为

(18)

2.2 MA算法的改进

1)引入反向学习

为了扩大算法的搜索空间，引入反向学习策略。反向学习的表达式为

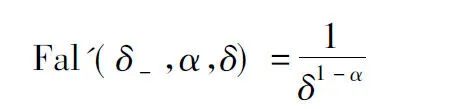
(19)

式中分别为猴群个体i在j维上的位置值和反向位置值；aj与bj分别为j维的下界与上界。

2)引入自适应权重系数

为了提高MA算法的全局寻优能力与局部寻优能力,参数的自适应计算公式如下

(20)

式中分别为s1与s2的最大值与最小值； (s4-s3)max,(s4-s3)min分别为(s4-s3)的最大值与最小值；Max_iter为最大迭代次数。

3)引入混沌正余双弦搜索机制

Logistic映射公式为

Zk+1=μZk(1-Zk)

(21)

式中Zk为(0,1)空间的数值；μ为Logistic映射控制参数，取值范围为[0,4]。当候选解取值范围为[lb,ub]时，实数域空间与(0,1)空间的转换关系为

X=lb+(ub-lb)Z

(22)

式中Z为Logistic映射后得到的数值；X为在[lb,ub]范围内Z所对应的实数值。

以候选解作为初始最优值，采用正余双弦算法进行搜寻，搜寻公式为

(23)

式中S为得到的新解；S*为搜寻过程中得到的最优值；r1取值如式(24)所示

(24)

式中τ为正常数；h为当前搜寻次数；H为预设的总的搜寻次数。Metropolis接受准则计算公式为

(25)

3 仿真与实验分析

3.1 仿真结果分析

为证明所提方法的有效性，使用MATLAB搭建了IMA算法优化改进型ADRC的PMSM仿真模型。PMSM参数如表1所示。

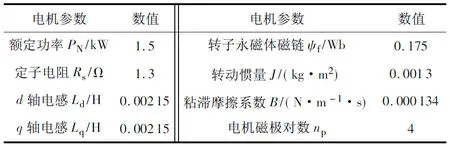
表1 永磁同步电机参数设置

1)高速工况下突加负载:给定PMSM转速为1 000 r/min，运行至0.2 s时突加10 N·m负载转矩。仿真结果如图2、图3所示。

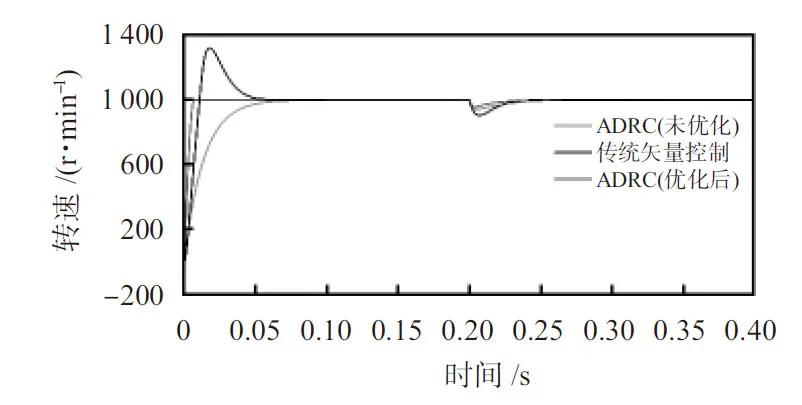
图2 突加负载时的转速波形

图3 突加负载时的转矩波形

2)高速情况下改变参考转速:给定PMSM初始转速为1 000 r/min，运行至0.2 s时将参考转速设置为-1 000 r/min。仿真结果如图4、图5所示。

图4 改变参考转速时的转速波形

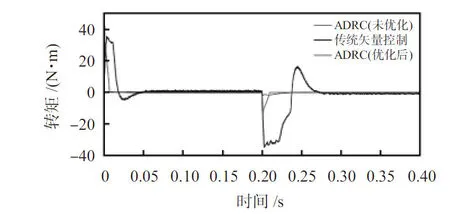
图5 改变参考转速时的转矩波形

3)低速工况下突加转矩:仿真设置为给定PMSM转速为100 r/min，运行至0.2 s时突加负载转矩10 N·m，仿真结果如图6所示。

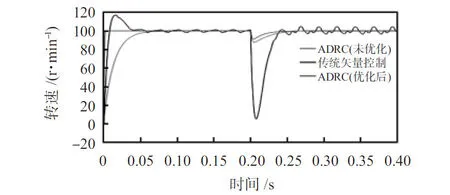
图6 突加负载时的转速波形

3.2 实验结果分析

本文以TMS320F28035DSP芯片为基础，搭建了PMSM控制系统实验平台。该实验平台主要由控制电路板、两台参数一致的电机、示波器、电脑、断路器组成。且安装有扭矩传感器、速度传感器。本文所提出的控制算法和软件程序在CCS软件中编程实现，并通过仿真器下载到F28335DSP芯片中。在空载的情况下启动进行实验。

分析图7，当负载发生突变时，基于IMA优化改进型ADRC控制器的PMSM转速恢复至参考值的时间相较于传统ADRC来说更短，且能够有效降低电机在转矩突变时所带来的转矩脉动。

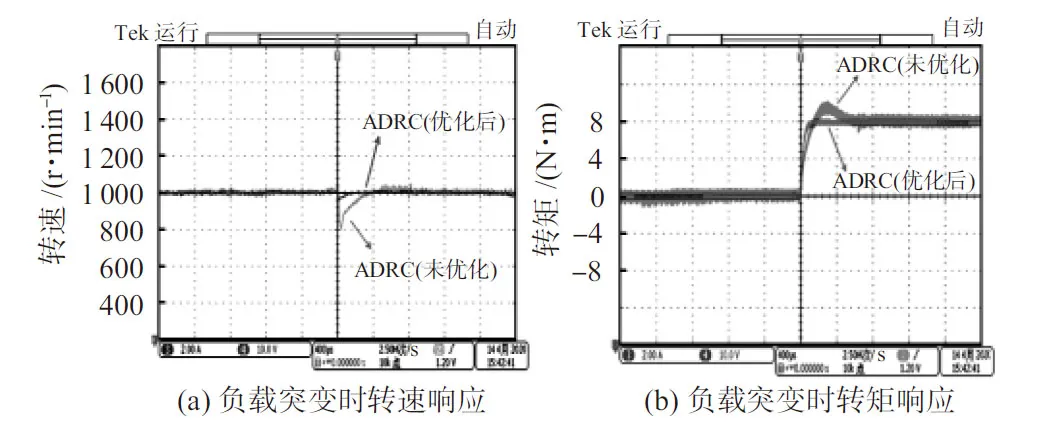
图7 负载突变时转速与转矩的响应测试

4 结 论

为了提高PMSM控制系统的鲁棒性和动态响应速度，本文提出了一种利用差值拟合法对ADRC的控制函数进行重构，得到了一种新型的ADRC控制器的方法，并将其应用于PMSM的性能调节。此外，考虑到ADRC控制器待整定参数较多，本文采用MA算法对其进行整定，并针对传统MA算法的不足，提出系列改进策略。最后通过实验结果分析可知，本文所提ADRC控制器改进策略可明显提高PMSM控制系统的控制精度与鲁棒性。