基于SAD-PE的自动睡眠分期模型

李令环, 奚峥皓, 曹 乐, 张文艳

(上海工程技术大学 电子电气工程学院,上海 201620)

0 引 言

早期睡眠分期主要是通过专家进行手动分期,由于不同睡眠时期之间的相似性较高,导致不同专家的判读结果一致性只有83 %左右。针对人工睡眠分期效率低、准确性不高的问题,研究人员提出自动分期的方法。睡眠自动分期模型大多是由一个睡眠特征空间再结合机器学习算法组成。现阶段睡眠特征提取大多是基于时域[1]、频域和非线性特征[2]。其中，使用较多的机器学习算法有决策树(decision tree,DT)[3]、随机森林(random forest,RF)[4]、支持向量机(support vector machine,SVM)[5]等。

睡眠脑电(electroencephalography,EEG)是研究人脑活动以及诊断和监测神经系统疾病的重要来源。其中,中枢性睡眠呼吸暂停和额叶癫痫等疾病常见于N1期与N2期,许多神经系统疾病(如帕金森氏病)则多出现在REM期。因此,N1期与REM的检测在睡眠分期中具有特殊的意义。但是,N1期的低识别率是众多分期模型普遍存在的问题,一方面是N1期比其他时期样本量少,另一方面是N1期与REM期背景波相似,二者存在非线性特征混叠现象[6],这就导致易将N1期误分类为REM期。研究人员正在设计出越来越多细粒度的特征信号解决这一问题。

睡眠EEG具有非平稳性和易受噪声扰动的特性[7]。因此,在进行分期前,本文提出一种基于符号化振幅差值(symbolic amplitude difference,SAD)的预处理方法,并对符号化结果计算排列熵 (permutation entropy,PE)。接着将符号化重构子向的均值作为权重加入到PE的计算,得到符号化振幅差值排列熵(SAD-PE),并给出影响SAD-PE特异性的尺度因子的计算模型。然后提取31个多域特征,并通过ReliefF算法计算SAD-PE和31个特征的贡献度排名并降维。最后选择贡献度累积超过90 %的特征组合送入分类器中进行自动分期。

1 数据来源

本文实验数据来自Sleep-EDF数据库。SC库的数据(sc4002e0,sc4012e0,sc4102e0和sc4112e0)是包括受试者全天活动的数据,而ST库的数据(st7022j0,st7052j0,st7121j0和st7132j0)则是在医院采集的整晚睡眠数据。由于顶尖波是N1期的一个标志,而在中枢/额叶脑区经常出现顶尖波,并且睡眠EEG中的大部分节律可以在Fpz-Cz通道捕捉,因此,本文选择Fpz-Cz通道的数据进行睡眠分期。该数据集中W,N1,N2,N3和REM期占比大约为68 %,2.6 %,16.7 %,5.4 %和7.2 %[8]。本文将数据库中SC和ST库中的样本分别标记为SC1，SC2，SC3，SC4和ST1，ST2，ST3，ST4,表1列出了本文使用的实验数据。

表1 各睡眠时期的数量

2 特征提取方法

2.1 SAD-PE

随着睡眠深度的增加,大脑活动由强变弱,图1为5个睡眠阶段振幅差值(amplitude difference,AD)的计算结果。

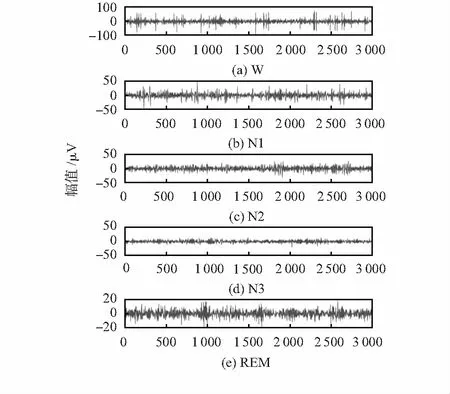
图1 各睡眠阶段的AD

由图1可知,REM期的AD基本在20 μV以下。而N1期,超过20的点明显多于REM期。为了更好地描述AD的分布,本文设置阈值T,统计各睡眠阶段AD大于T的点的个数,记为n。本文将阈值设置在20附近,步长 1,逐点统计不同阈值下n的平均值。

结果显示,N1期与REM期在不同阈值下呈现出较为明显的差别。在T>21时,REM期n的个数出现小于1的情况,而N1期仍存在较多大于21 μV的点。本文提出用SAD-PE 进一步刻画这一特性。具体计算过程为:假设睡眠EEG信号X=(X1,X2,…,Xn),n=1,2,3,…,N,其中，N=3 000,对睡眠EEG相邻两点求差并取绝对值得到AD。然后将AD进行符号化,公式如下

(1)

本文取比例因子a调整AD的带宽。a的选取一定程度上决定了SAD-PE的特异性。假定符号化后的EEG为Xi=(x1,x2,…,xn),n=1,2,3,…,N。当嵌入维数为m时,对符号化结果进行相空间重构可得到

i=1,2,…,N-(m-1)

(2)

(3)

(4)

Pwi=Pi×wi

(5)

(6)

式中 log以2为底,HSAD-PE(m)达到最大值时为log(4m),将HSAD-PE(m)进行标准化,得到SAD-PE

(7)

2.2 SAD-PE的参数计算

传统PE计算时,建议取3,4,5,6,7[9]。计算SAD-PE时,取m=3(43=64),排列模式数量少,无法全面表征EEG的振幅波动性,取m=7(47=16 384)没有意义,因此,本文给出当m取4,5,6时,ST1连续1 h睡眠EEG的SAD-PE曲线，如图2所示。

图2 不同m值下的SAD-PE曲线

当m取4,5,6时，基本上不影响整体变化趋势,为了提高计算速度,取m=4。本文将8个样本在α取不同值时，得到的SAD-PE绘制如图3、图4。

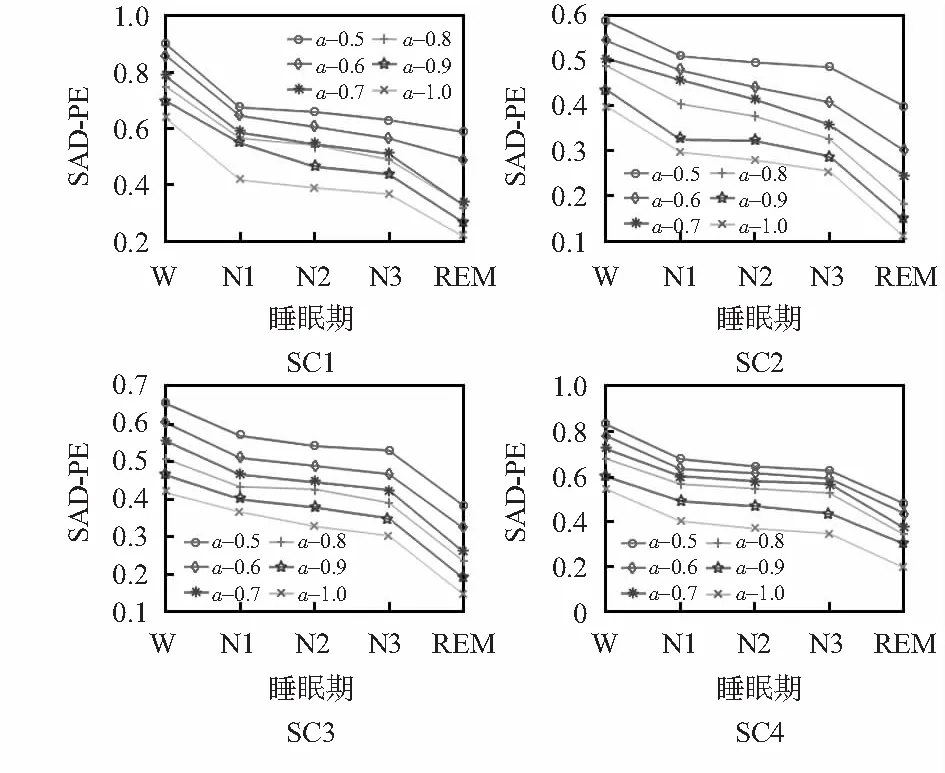
图3 SC样本在a取不同值时的SAD-PE

图4 ST样本在a取不同值时的SAD-PE

SC样本与ST样本总体趋势表现出一致性,均随着睡眠深度的增加,SAD-PE逐渐变小,这符合大脑活动由强变弱的生理过程。为了确定a为何值时,SAD-PE在睡眠各期,尤其是在N1期与REM期特异性最高,本文结合现阶段研究成果中[8,10]的混淆矩阵,定义评价指标(evaluation index,EI)

EI=W1×|HSAD-PEN1-HSAD-PEREM|+W2×|HSAD-PEN1-HSAD-PEN2|+

W3×|HSAD-PEN2-HSAD-PEN3|+W4×|HSAD-PEN2-HSAD-PEREM|

(8)

为减小数据不平衡对分类准确度的影响,W1,W2,W3,W4的值根据睡眠时期数量占比确定。本文以W1为例

(9)

(10)

同理求出W2,W3,W4。本文W1,W2,W3,W4分别取0.500 6,0.077 8,0.240 9,0.180 7。基于式(8),计算样本的EI平均值,如表2所示。

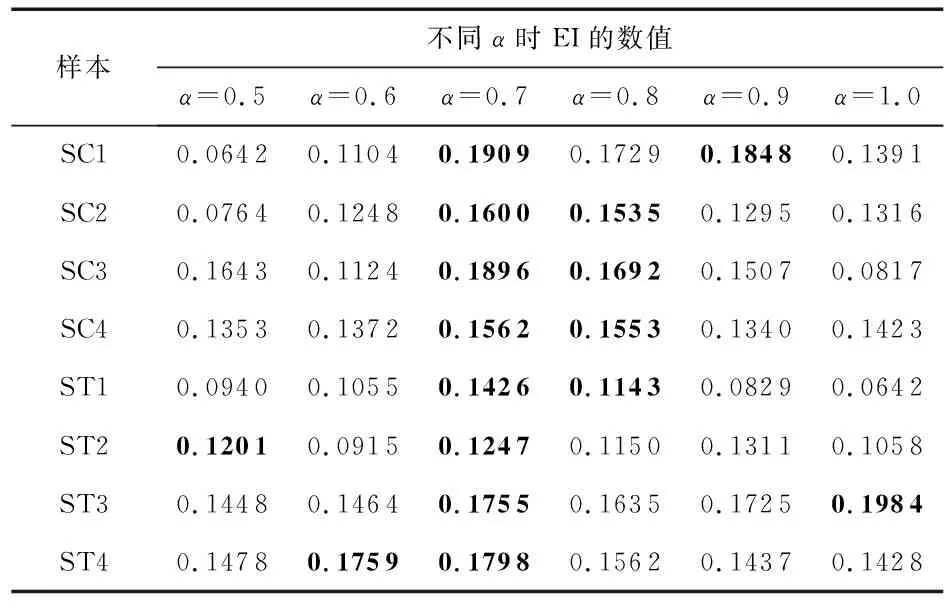
表2 a取不同值时EI的平均值

在a=0.7时,各样本EI值均处于前2名,本文在后续特征提取时,取a=0.7。

3 实验验证与结果分析

3.1 基于ReliefF的特征贡献度验证

本文从时域、频域、时频和非线性4个方面提取31个特征,加入a=0.7时的SAD-PE,一共32个特征用于自动分期。本文用ReliefF算法验证SAD-PE的贡献度并进行特征降维。在ReliefF算法运行50次后,结果显示,排名靠前的20维特征向量累积贡献量达90.65 %。为了提高计算效率,本文选择20维特征向量进行模式识别。将20维特征重新用ReliefF算法运行50次,表3给出了具体特征和归一化的特征贡献度值。

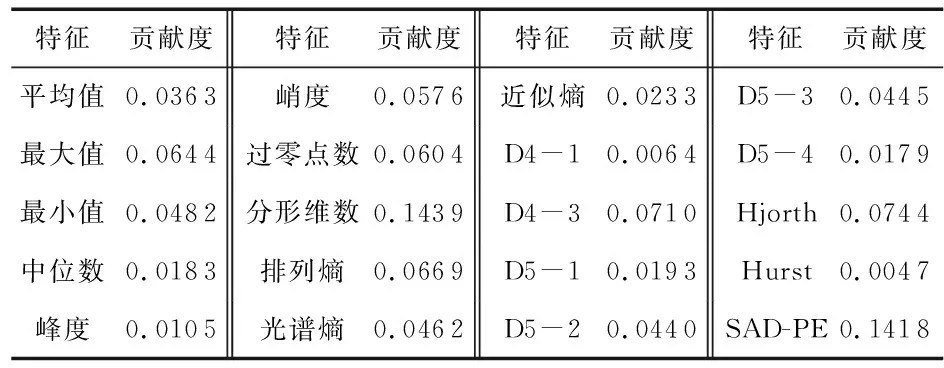
表3 特征和特征贡献度值对照表

其中，D4—1,D4—3,D5—(1—4)表示基于Daubechies小波分解的睡眠EEG信号的D4,D5层细节子频带系数。本文提出的SAD-PE的特征贡献度排名靠前,表明其能够作为睡眠自动分期的有效特征。

3.2 评价指标

使用召回率Rec、精度Pre,F1-Score(F1)三个指标来评价各个睡眠时期的性能。用K系数和准确性Acc评价整体分类性能,公式如下

(11)

(12)

(13)

(14)

(15)

式中TP,TN,FP和FN分别为真阳性,真阴性,假阳性和假阴性。假设每类的真实样本个数为T1,T2,…,TN,而预测每类样本的个数为P1,P2,…,PN,总样本个数为N,则Pe计算公式如下

(16)

3.3 结果与分析

在8个样本的睡眠EEG中截取5 760组数据作为本文数据集。每次随机抽取3 840组数据作为训练集,其余1 920组数据作为测试集,将表3中的20个特征输入到C4.5,RF和SVM中进行分类测试。经过10 次验证,将结果最佳的1组如表4～表6。由表可知：C4.5、RF、SVM分类的Acc分别为85.68%,87.50%,86.72%，Kappa分别为80.31 %,82.54 %,81.84 %。

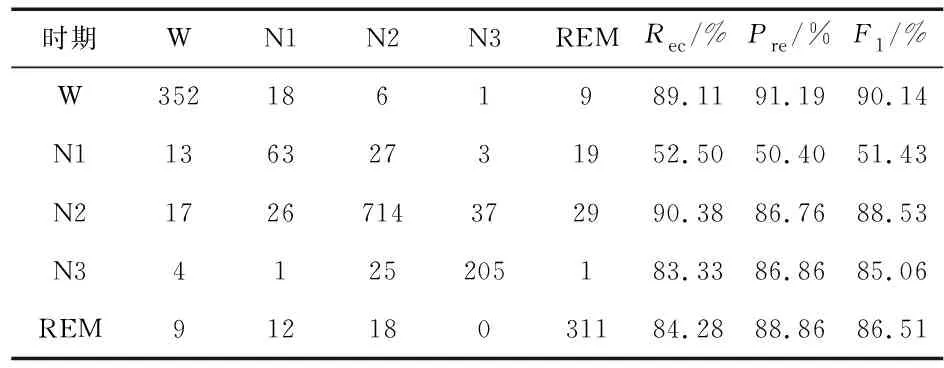
表4 C4.5分类结果混淆矩阵

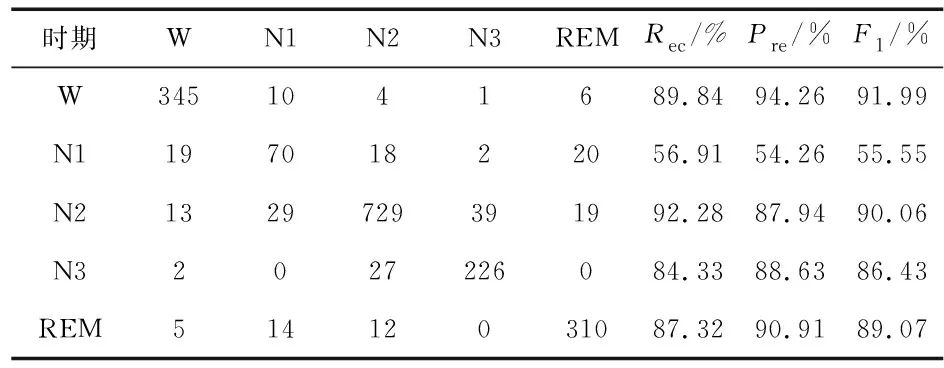
表5 RF分类结果混淆矩阵

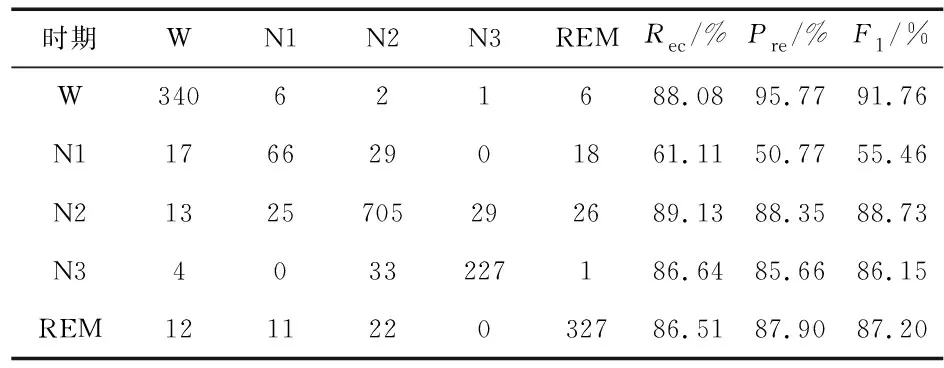
表6 SVM分类结果混淆矩阵

其中,识别率最高的是W期,准确度都在90 %以上,因为W期脑电活动丰富,本文提出将子向量的均值作为权重加入到SAD-PE的计算中,扩大了W期与其它时期的差异性。 N2期、N3期和REM期准确度和都在85 %以上,因为N2和N3期的特征波形为振幅最大的睡眠纺锤波,而REM期因为锯齿波的存在,导致REM期AD在一个相对平稳的范围,使得N1期、N2期和N3期的SAD-PE都大于REM期。N1期的分类准确度在50 %以上,相较于其他时期识别率较低。但是,本文所提方法在N1时期的分类准确度仍高于列表7中列出的其他模型。

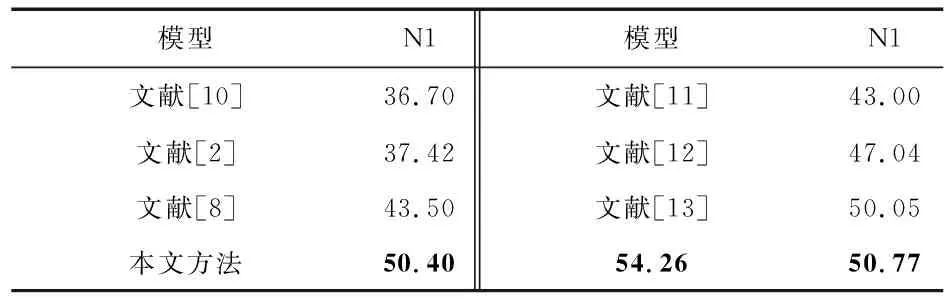
表7 N1期分期准确度比较 %

对比实验中,3个分类器中表现最好的是RF,其为87.50 %,为82.54 %,本文将RF的结果与相同实验条件下的已有分期模型进行对比,如表8所示。

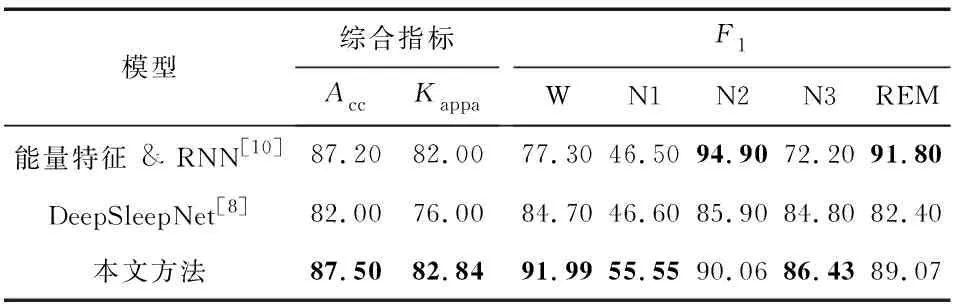
表8 结果对比 %

本文的Acc和Kappa略高于现有成果。值得一提的是在N1期的分类准确度明显高于其他模型,归因于本文对PE的改进。首先,在确定值时,结合误分类程度和原始数据占比给出EI的计算模型,一定程度上减小了数据不平衡对分类结果的影响;其次,考虑到N1期大脑仍处于比较活跃的状态,AD变化较REM期更明显,且REM期出现的锯齿波使得AD分布在较小范围,提出将重构子向量的均值作为权重更新PE的计算结果,从而扩大N1期与REM期的差异,一定程度上解决了N1期与REM期在非线性特征提取时出现特征值混叠的问题。

4 结 论

提出一种SAD的预处理方法,将睡眠EEG相邻两点的振幅差值进行4符号化。并针对传统PE算法只保留重构子向量顺序结构、丢失波形振幅信息的问题,提出将重构子向量均值作为权重,添加到PE的计算中,得到SAD-PE。然后,结合8位受试者的真实睡眠EEG绘出不同值下的SAD-PE,并给出了影响SAD-PE特异性的计算模型。利用ReliefF算法验证SAD-PE的有效性并进行降维,将降维后的20个特征送入3种分类器中进行自动分期。结果表明,本文所提基于SAD-PE的自动睡眠分期模型可以有效地表征睡眠EEG的振幅波动性,并且对N1期的识别准确度高于现有方法,给分析N1期与REM期相关的异态睡眠提供了新的思路,具有较好的应用前景。