改进麻雀搜索算法在WSNs覆盖优化中的应用*
徐光宪, 丁瑞峰
(辽宁工程技术大学 电子与信息工程学院,辽宁 葫芦岛 125105)
0 引 言
随着5G通信技术和人工智能的快速发展,进而推动了移动通信技术和移动设备的更新换代,这使得无线传感器网络(wireless sensor networks,WSNs)的应用越来越广泛[1],在航空、环境 、农业、医疗等领域取得显著的成果。在WSNs中首要解决的问题就是覆盖质量,而传统的随机节点部署会造成节点密度大和覆盖率低等问题,进而影响网络通信性能。因此,如何高效地部署传感器节点成为一个重要的研究话题[2]。
近年来,群智能优化算法在解决WSNs的覆盖质量问题上取得了显著成果。文献[3]提出使用萤火虫算法的WSNs覆盖最大化方法;于文杰等人[4]提出基于外推人工蜂群算法的节点部署优化方法;胡小平等人[5]提出改进灰狼优化算法(improved gray wolf optimization algorithm,IGWOA)在WSNs节点部署中的应用;张亮等人[6]提出基于模糊粒子群优化算法的WSNs的节点部署优化方法;宋婷婷等人[7]提出基于改进鲸鱼优化算法(improved whale optimization algorithm,IWOA)的WSNs覆盖优化方法。上述各类研究方法中,虽然对WSNs节点部署取得了一定成果,但在实际应用过程中,在要求高覆盖率、高收敛性、高精度等方面仍有待提高。
本文为了使节点部署达到较高的覆盖质量,在麻雀搜索算法(sparrow search algorithm,SSA)[8]的基础上,提出一种混合策略改进的SSA(mixed-strategy SSA,MSSA)的覆盖优化方法。首先,利用反向学习策略,解决种群初始化问题;其次,利用鲸鱼算法的随机搜索策略改进麻雀发现者的位置更新方式,提高种群的全局搜索能力,最后,利用萤火虫算法对麻雀个体进行扰动更新,使其具有跳出局部最优的能力。
1 WSNs的覆盖模型
假设WSNs监测的目标区域是经过离散化的面积为L×M的二维平面,在此二维平面部署具有一样感知半径R和通信半径Rc的N个同构传感器,Z={z1,z2,…,zN}为所有传感器节点的集合。WSNs中节点感知模型使用布尔模型[9],假设某个传感器节点zi的位置坐标为(xi,yi),被监测点Tj的位置坐标为(xj,yj),则传感器节点与被监测点的欧氏距离为
(1)
用p(zi,Tj)表示传感器节点zi对Tj是否感知,当Tj的位置在以传感器节点zi为圆心的圆内时,则表示被感知记为1;否则记为0,数学表达式为
(2)
假设多只传感器对同一个目标点协同探测时,WSNs对目标点的感知质量为
(3)
群智能算法对求最小值问题有显著的效果,因此,将求高覆盖率问题转换为求最小值问题,目标函数表示为
(4)

2 SSA
SSA过程主要包括发现者模型和追随者模型,同时还设置了一定比例的个体作为预警机制,其中,发现者和警戒者的比例各占整个种群的10 %~20 %。发现者在种群中起引领作用,为整个种群寻找觅食区域和提供飞行方向,而追随者则是通过追随发现者来获取食物,警戒者负责食物区域周围的警戒。在觅食过程中,三者位置会不断更新,进而获取最优食源,最优食物的位置即为寻得的最优解。
2.1 发现者的位置更新方式
(5)

2.2 追随者的位置更新方式
(6)
式中Xp和Xworst分别为当前发现者最优和全局最差位置。A为每个元素随机赋值为1或-1的矩阵,并且A+=AT(AAT)-1。n为种群个数,当i>n/2时,这表明第i个追随者适应度函数值较低,即没有获得足够的食物,此时追随者变为发现者需要去其他区域寻找食物。否则,向当前发现者最优位置Xp移动。
2.3 警戒者的位置更新方式
(7)
式中Xbest为当前全局最优位置。β为随机正态分布的步长因子。K为种群的步长控制系数,其中,K的区间为[1,1]。fi为麻雀的适应度值,fg和fw分别为当前全局最佳和最差适应度值。ε为防止分母取零的最小常数。当fi>fg时,表示作为警戒者的i只麻雀不在全局最优位置,意识到危险逃到Xbest的附近。当fi=fg时,表示作为警戒者的i只麻雀在全局最优位置,意识到危险逃到自身附近。
3 MSSA
3.1 反向学习策略初始化种群
在种群初始化时,大部分智能优化算法都是在搜索空间内随机生成初始种群,这种随机生成初始种群个体的位置多样性不足,影响最终的全局最优值的输出。因此,本文利用反向学习策略[10]初始化种群弥补不足,其策略如下:


图1 反向学习策略前后种群位置
3.2 发现者位置更新策略的改进

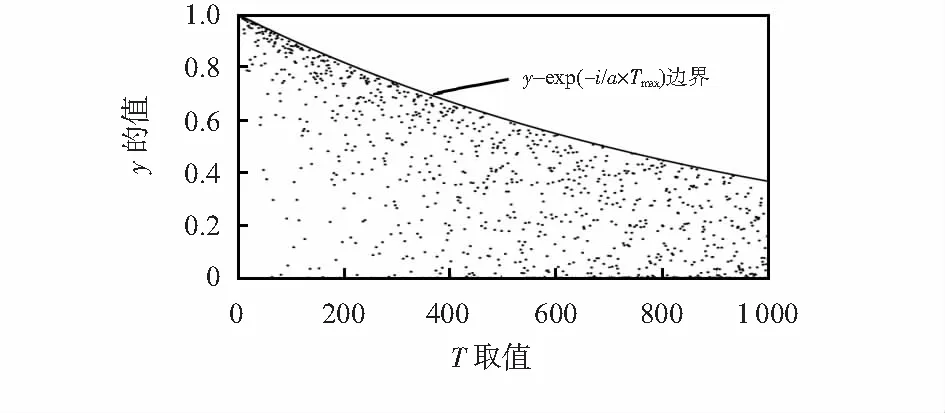
图2 函数y和麻雀位置更新的变化趋势
为了解决上述问题,利用鲸鱼算法[11]中的随机搜索策略进行改进,公式如下
(8)
式中Xrand为一个随机的鲸鱼位置,A=2ar1-a,C=2r2,a=2-2t/Tmax。其中,r1和r2为[0,1]均匀分布随机数;a为从2到0线性递减的收敛因子。A作为步长系数是鲸鱼算法寻优过程的重要参数,主要取决于收敛因子a。

图3 步长A的更新方式
如图3可知,改进后麻雀个体搜索方式可以从自身的正反两个方向进行位置更新,大大提高了前期麻雀算法的搜索空间,同时提高了后期种群的收敛速度,能够使麻雀种群更快的收敛。所以,发现者的位置更新改进为
(9)
3.3 追随者位置更新策略的改进

(10)
改进后的模型在最优解位置周围随机移动,使得其局部搜索能力提高,最终会收敛于最优解的位置。
3.4 萤火虫扰动策略
为了避免算法陷入局部最优的问题,在麻雀每代个体位置更新后用萤火虫算法[12]对麻雀个体进行位置扰动更新,使其具有跳出局部最优的能力。扰动后的麻雀个体与扰动前的麻雀个体进行适应度函数的对比,如果更优则更新麻雀位置。萤火虫扰动位置更新模型为
(11)
式中xi为最优麻雀的位置,xj为剩余所有麻雀的位置,β0为最大吸引度,γ为一般取1的光强吸收系数,ri,j为麻雀位置xi与xj之间的空间距离,α∈[0,1]为步长因子,rand为[0,1]区间服从均匀分布的随机数。原步长因子是个常数变量,不能满足算法前期广泛搜索,后期精细搜索的要求,因此,将扰动步长因子α改进,改进后公式为α=2/πarccos(t/Tmax),且如图4所示。
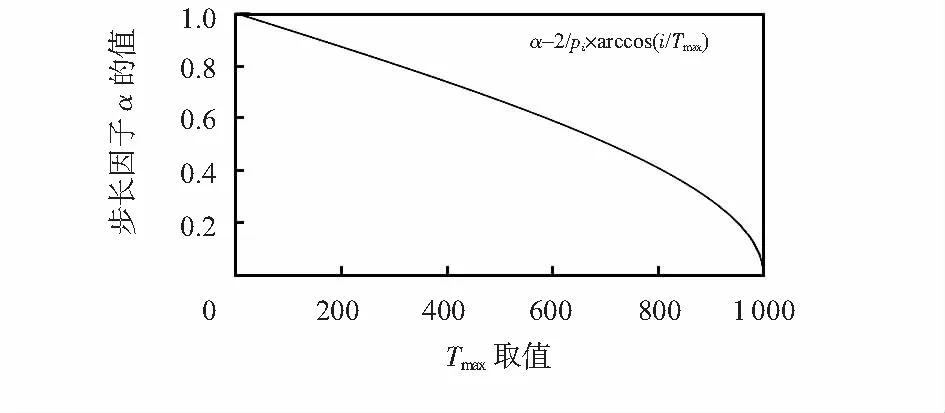
图4 非线性步长因子
3.5 基于MSSA的覆盖优化过程
将麻雀觅食过程运用到覆盖优化问题中节点位置寻优过程中,麻雀位置的每代更新为节点的位置更新,利用目标函数值的好坏激励麻雀位置更新,使其取得最优解。
Step1 输入监测区域、WSNs和MSSA的相关参数。
Step2 利用反向学习策略初始化种群。
Step3 根据式(4)计算种群适应度值,对适应度值进行排序,找出位置最优和最差的个体。
Step4 麻雀发现者、追随者、警戒者分别根据式(9)、式(10)、式(7)进行位置更新。
Step5 将所有麻雀与最优位置麻雀利用萤火虫扰动公式(11)进行位置更新。
Step6 重复Step3,判断迭代循环次数是否满足结束条件,若达到,算法执行结束,输出结果。否则,跳转到步骤4继续进行。
4 仿真实验与分析
4.1 实验环境
为了验证MSSA在WSNs覆盖优化问题中节点部署的实际情况,利用MATLAB环境进行了仿真,将MSSA,SSA和文献[5]中的IGWOA和文献[7]中的IWOA的节点部署情况进行对比。
4.2 实验结果
4.2.1 监测区域为20 m×20 m覆盖优化对比
实验参数设置为监测区域为的20 m×20 m二维平面,种群个数为40,传感器节点数为24,感知半径为Rs=2.5 m,通信半径为Rc=5 m,迭代次数为1 000次。表1为各算法平均覆盖率优化结果对比。图5为覆盖优化迭代收敛曲线,图6为各算法优化后的WSNs的节点部署。

表1 平均覆盖率优化结果对比
由表1可知,MSSA与SSA、IGWOA和IWOA的优化结果相比,覆盖率分别提升了16.30 %、6.55 %和4.28 %。从图5中可知,MSSA在迭代319次陷入局部最优,经过萤火虫算法扰动后,跳出局部最优,在迭代493次达到全局最优解,且所求覆盖率优于其他算法。从图6中各算法优化后的节点部署可知,SSA优化后的节点部署中覆盖盲区较大,IGWOA和IWOA优化后的盲区相对较小,而MSSA优化后的结果使传感器节点分布更均匀。
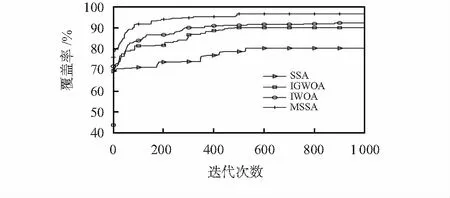
图5 覆盖优化迭代收敛曲线
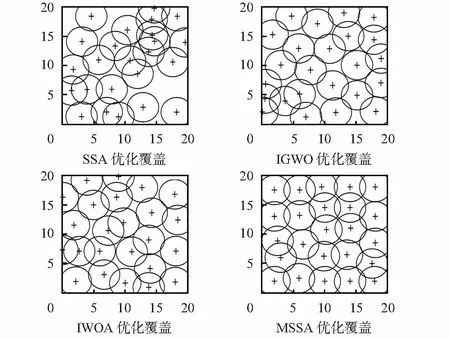
图6 各算法优化后的节点部署
4.2.2 监测区域为100 m×100 m覆盖优化对比
实验参数设置为监测区域100 m×100 m的二维平面,种群个数为40,传器节点数为40,感知半径Rs=10 m,通信半径Rc=20 m,迭代次数为1 000次。表2为各算法平均覆盖率优化结果对比。图7为覆盖优化迭代收敛曲线,图8为各算法优化后的WSNs节点部署。
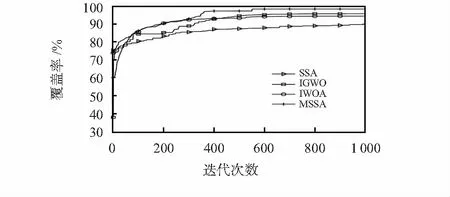
图7 覆盖优化迭代收敛曲线

图8 各算法优化后的节点部署
由表2可知,MSSA与SSA、IGWOA和IWOA的优化结果相比,覆盖率分别提升了7.44 %、2.62 %和3.93 %。由图7可知,MSSA在收敛速度上不断向最优值靠近,在362代陷入局部最优,通过萤火虫扰动跳出局部最优后,在556代达到全局最优。通过图7和图8可知,MSSA在求最优解和节点部署的效果方面都要优于其他算法。

表2 平均覆盖率优化结果对比
从上述在两种不同监测区域的实验结果表明,MSSA在优化WSNs覆盖问题上,能够很好地解决节点冗余、覆盖率低等问题,相比于其他算法具有一定的优势。
5 结 论
本文对于WSNs中随机节点部署时容易造成WSNs覆盖质量率低的问题,在SSA的基础上提出MSSA,对该问题进行优化。首先,利用反向学习策略初始化种群,增加种群的多样性和遍历性;其次,借鉴WOA中随机搜索策略对SSA中发现者位置更新进行改进,提高算法的全局搜索能力;同时,对追随者位置更新中的收敛于零点的部分进行优化,提高算法局部搜索能力;最后,利用萤火虫扰动策略对最优麻雀个体进行扰动更新,使算法具有跳出局部最优的能力。实验结果表明:MSSA相比于其他算法具有适应性强和收敛性较为稳定的特点,同时也使得区域覆盖面积有了显著的提高,减少了节点冗余度。

