DRNN在多传感器泥石流监测系统中的应用*

徐根祺, 曹 宁, 谢国坤, 马 婧, 南江萍, 张佳绮

(1.西安交通工程学院 机械与电气工程学院,陕西 西安 710030; 2.西安交通工程学院 土木工程学院,陕西 西安 710030;3.中国葛洲坝集团第三工程有限公司,陕西 西安 710119)

0 引 言

在地质灾害防治过程中，为了分析泥石流监测系统的实时数据信息和准确预测其发展变化趋势，需要在灾害常发地收集有效信息[1～3]，利用无线传感器网络(WSNs)在线实时监测是目前主要采用的方法[4]。泥石流灾害监测系统中所需传感器众多，这些传感器以分布式无线传感器网络的形式搭建而成[5～7]。崩塌、滑坡等地质灾害产生的固体松散物质会对网络的正常工作造成干扰甚至破坏网络节点，传感器及电池板上长期堆积的灰尘也会造成传感器采集数据不准确、采样周期改变或数据丢失等情况[8～10]。

针对网络故障导致的数据异常问题，利用集中化的全局通信方式成本太高；采用分散式，基于相邻传感器节点间不同数据信息的故障进行判断[11～12]的方法，需要所有传感器测量同一变量为前提，然而，传感器监测的并非都是同一变量；基于图形的方法隔离网络中的故障点，利用时间序列与时间窗口之间的相互关系对故障节点进行判断，精度无法得到保证。

为了解决当前研究中存在的问题，本文利用回声状态网络(echo state network，ESN)在整个传感器网络上搭建一个大型的分布式递归神经网络(distributed recurrent neural network，DRNN)，网络节点间使用局部通信的方式，每个传感器节点只配置较少的神经元，只有相邻节点之间进行通信。当有传感器节点发生故障而导致数据异常时，相邻节点使用DRNN的预测值向其他节点传输数据，泥石流监测预警系统使用预测值对泥石流的发生概率进行预测，从而保证泥石流监测预警系统在恶劣环境下的预报精度。

1 ESN

ESN的内部神经元之间以线性变换的方式进行连接[11]。ESN在递归层中的连接权值矩阵随机生成后保持不变，并且在训练过程中，只改变与输出单元的连接权值[12,13]。训练完成后，连接权值将不再改变，输出和下一时刻的网络状态由当前时刻的输入和内部状态决定，因此，该网络的训练复杂度较低[14,15]。

fxt+1=F(fxt,fut)

(1)

fyt+1=F(fyt,fut)

(2)

若系统F(·)与外部输入状态fut无关，且∀(fx0,fy0)，若满足∀ε>0，∃δ(ε)>0,当t≥δ(ε)时，d(fxt,fut)≤ε恒成立，则称系统满足“回声状态条件”。

2 DRNN

2.1 理论基础

设传感器节点数为M，第m个节点上的输入神经元数为Km，隐含层神经元数为Nm，输出神经元数为Lm。输入神经元数、内部神经元数、输出神经元数分别为

(3)

分别将输入、隐含层和输出表示为以下列向量的形式

(4)

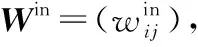
x(n+1)=f(Winu(n+1)+Wx(n))

(5)

式中x(n+1)为各传感器数据，f为内部神经元的激活函数f的向量函数f=tanh，选取双曲正切函数作为激活函数，输入与输出之间为线性关系。

2.2 DRNN结构

为节省占用的内存，因此，在全网络内仅搭建一个DRNN，从而仅利用相邻节点间的通信，实现“回声状态条件”。和ESN一样，DRNN在递归层中使用随机生成且保持不变的神经单元——储备池，并且在训练过程中只改变与输出单元的连接权值。

每一个网络节点都分布有神经元，将神经元之间的连接限制在传感器节点附近，这样就可以在传感器网络上布置一个DRNN，DRNN的所有内部连接权值随机生成后不再改变。此外，为了进一步减少节点间的通信，仅在同一个传感器节点上施加输入，输出与所有传感器节点相连，输出单元从储备池的部分区域和邻近节点的储备池获取输入。

由于激活向量分布在多个传感器节点上，不同节点之间也会有连接，因此，需要为其指定存储空间，以存储相邻传感器节点上神经元的输入权值。输出神经元仅向前激活相邻节点的神经元，而不对其权值进行更改。作为之前指定的存储相距较远节点数据的相邻神经元，需要使用相同的时间间隔来处理数据，利用代理神经元可以满足这样的需求。将更新后的连接权值传送到相邻的代理神经元，相邻节点就可以使用该权值。该权值被使用以后，代理神经元存储的数据就会自动删除。这样就可以避免因两个节点之间通信失败而导致数据传输错误。

2.3 初始化DRNN

2.4 训练DRNN

以输入和输出神经元的时间序列作为训练数据。通过训练DRNN来预测邻近故障节点上的传感器数据。 首先，通过采集内部网络状态获取权值矩阵M和输出矩阵T。当训练数据传输到输入神经元时，采样过程完成;然后，从每一阶段的训练数据中，选取DRNN的一个内部激活向量和一个输出激活向量，采样到的数据存储在更新后的矩阵M和T中。通过隐含层神经元个数N，输出神经元个数L和训练步数S，最终得到S×N阶权值矩阵N和S×L阶输出矩阵T。在每个传感器节点上使用Mj和Tj来改变输出权值。Mj仅包含输入神经元、内部神经元和输出神经元的权值，Tj包括输出神经元的输出权值。利用式(6)计算每个节点的输出权值矩阵

(Wout)T=M-1T

(6)

3 实 验

3.1 数据来源

根据在陕西省山阳县12个地质灾害监测点布设的传感器，分别通过雨量传感器、土壤含水率传感器、孔隙水压力传感器、地声传感器、次声传感器和泥位传感器对相应的泥石流灾害影响因子数据进行监测[16]，选取其中1 000组数据用于网络训练。采用MATLAB软件进行仿真，仿真平台由6个传感器节点搭建而成，这6个节点排列在2×3的网格上，每个节点都有1只传感器，且各节点均可与邻近的节点进行通信，其结构如图1所示。

图1 传感器节点结构

3.2 实验分析

模拟10 %的传感器节点发生故障时的情形。开始使用100组数据进行训练，逐渐增加训练数据，最终达到1 000组，训练效果如图2所示。图中显示，土壤含水率传感器发生故障时系统预测泥石流发生概率的归一化根均方误差(normalized root mean square error,NRMSE)、孔隙水压力传感器发生故障时,系统预测泥石流发生概率的NRMSE和所有传感器分别发生故障时,系统预测泥石流发生概率的平均NRMSE。

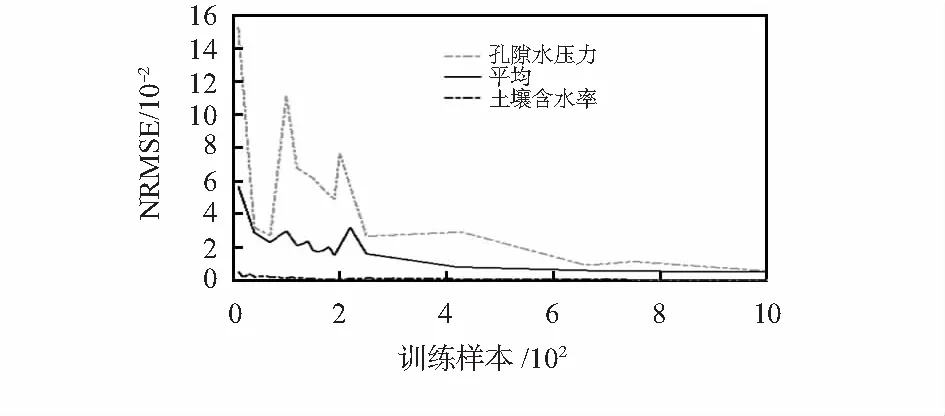
图2 不同训练样本的预测效果对比

土壤含水率传感器故障和孔隙水压力传感器故障时，泥石流发生概率预测值的NRMSE和平均绝对百分比误差(mean absolute percentage error,MAPE)的变化情况如表1所示。

表1 部分传感器故障时的NRMSE与MAPE对比

表1数据表明:当样本数据较少时，孔隙水压力传感器数据短时间内变化很大，该传感器数据对应的预测值MAPE变化较大,而NRMSE变化较小，因此,采用NRMSE对故障进行衡量更加可靠。对于数值变化较小的土壤含水率传感器数据，对应预测值的NRMSE和MAPE都较小，但显然用NRMSE来表征故障更合理。

将储备池神经元的数量从1个逐渐增加至30个，每个节点上的储备池神经元个数从1个增加到30个的NRMSE变化情况如图3所示。土壤含水率传感器故障和孔隙水压力传感器故障时，不同数量储备池神经元对应泥石流发生概率预测值的NRMSE和MAPE对比情况如表2所示。

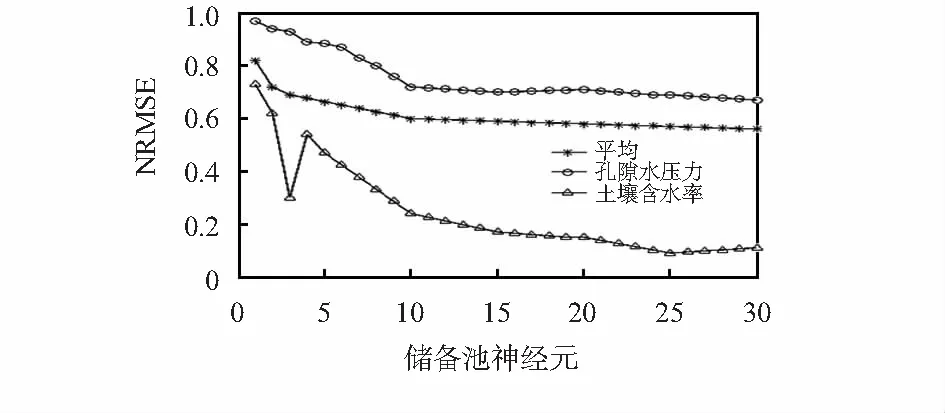
图3 不同储备池神经元数量的预测误差对比

表2 不同数量储备池神经元的NRMSE和MAPE对比

结合图3和表2可以看出，当只有孔隙水压力传感器发生故障时，储备池神经元数量较少的情况下，随着储备池神经元数量的增加,NRMSE逐渐减小，当储备池神经元数量增加到一定程度时，最终NRMSE趋于稳定；当只有土壤含水率传感器发生故障时，储备池神经元数量较少的情况下，NRMSE的变化并无明显规律，随着储备池神经元数量的增加，NRMSE逐渐减少，当储备池神经元数量增加到一定程度后，NRMSE反而呈上升趋势；对于所有传感器发生故障时的平均NRMSE，当随储备池神经元数量达到10时，平均NRMSE已经稳定，继续增加储备池神经元数量，预测效果并无明显变化。以上分析表明,为每个传感器节点分配一个ESN(采用全局通信的方式)，每个ESN上有120个内部神经元，相当于DRNN的每个节点上有20个内部神经元，对于泥石流发生概率为64.8 %的实验样本，分别从链路质量10 %开始，一直到链路质量100 %,对两种模型进行训练，结果如图4所示。表3列出了DRNN和ESN不同链路质量对应的NRMSE和MAPE。

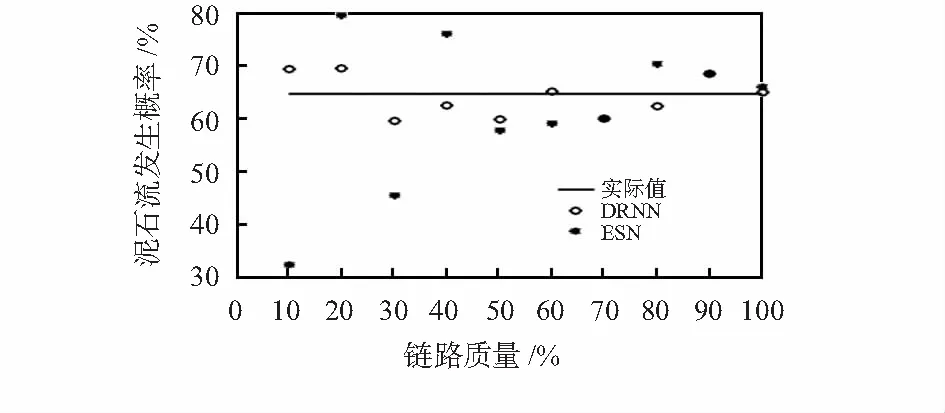
图4 不同链路质量预测结果

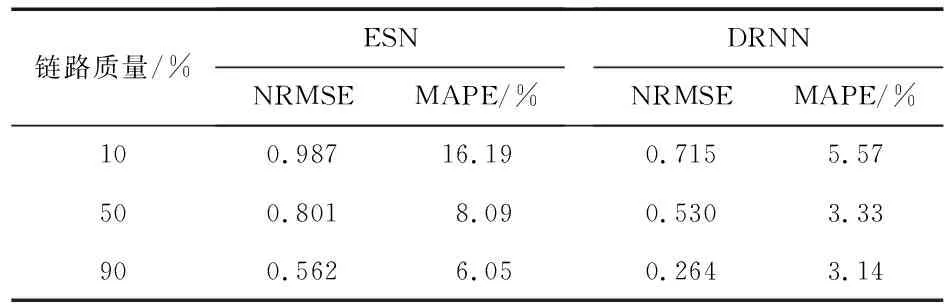
表3 不同链路质量的NRMSE和MAPE对比

从图4和表3中明显可以看出，当链路质量从10～100 %变化时，DRNN的预测结果始终在实际值附近变动，而ESN虽然最终的预测结果也很接近实际值，但是对于链路质量较差的情况，预测结果偏离实际值较远，预测效果并不理想。也就是说，随着链路质量的下降，使用ESN预测值的预测结果迅速发散。只有当几乎所有的传输数据都正常时，ESN才具有较好的效果。

采用十折交叉法进行验证，NRMSE如图5所示。从1 %的故障传感器开始，逐渐增加故障传感器的数量。从图5中两种不同方法的NRMSE对比曲线可以看出，当只有很少的传感器发生故障时，使用异常数据对泥石流发生概率进行预测和使用DRNN预测值对泥石流发生概率进行预测，误差NRMSE几乎一致且非常小。随着传感器故障数的增加，使用DRNN预测值对泥石流发生概率进行预测的NRMSE缓慢增加，当50 %的传感器节点发生故障时，NRMSE为0.35左右，直到传感器故障节点数超过90 %以后，NRMSE才急剧增加；而使用故障传感器反馈的异常数据对泥石流发生概率进行预测的NRMSE很快便达到0.5以上，最终几乎达到0.9。

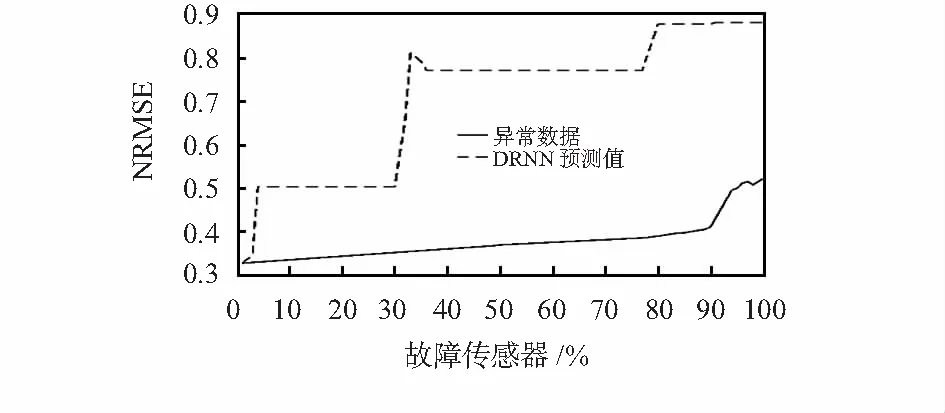
图5 DRNN预测值和异常数据预测效果对比

4 结 论

本文将DRNN引入多传感器泥石流灾害监测预警系统，当有节点发生故障或其他原因导致数据传输异常时，通过训练DRNN识别故障传感器，同时依据相邻节点信息对传感器数据进行预测，并利用预测值代替异常数据对泥石流发生概率进行预测。该方法保留了ESN计算复杂度低的优点，整个训练过程中，只有加法、乘法和激活函数tanh(x)的运算。

1)训练样本越多，DRNN训练效果越好，本文的研究仅基于1 000组的训练样本，故研究结果具有一定的局限性；

2)DRNN的训练效果取决于储备池神经元的数量，但并非储备池神经元数量越多，DRNN的训练效果就越好；

3)当链路质量下降时，DRNN依然具有比较好的预测效果；

4)对于由于恶劣环境因素影响而发生故障的情况，DRNN具有较好的可靠性。