ARCS动机模型的教学实践与思考
孔伟伟 毛亚玲


目前大部分习题课都是以教师教授为主,学生是知识的被动接受者,造成学生不喜欢学习数学,认为数学学科难度较大.如何更好地激发学生学习数学的兴趣和动机,努力提高数学习题课的教学质量,成为数学教师必须重视的一个问题,为此,笔者以整体视角设计以“轴对称图形”为主题的习题课,借助“折纸活动”以兴趣为引领、问题为驱动,让学生在解决形式多样的问题过程中,维持学生的学习动机,增强学生学习数学的信心.
1ARCS动机模型模型简介
ARCS动机模型是由J.M.Keller提出来的,它从四个方面激发学生的学习动机,即注意(Atten-tion)、相关性(Relevance)、自信(Confidence)和满足感( Satisfaction).注意即借助多种形式吸引学生的注意,唤醒学生的学习动机;相关性指教学既要紧密联系学生生活实际,也要建立在学生已有的知识经验上,才能引发学生数学学习的自然和自觉;自信是数学问题解决的心理前提,在教学中,基于学习需要将问题梯度化、教学目标明确化,使学生都能参与活动,不断激发学生的自信心;满足感就是通过学生自身努力,使学习结果和自己的期待一致,从而产生继续学习的欲望.
2“轴对称图形”习题课教学中ARCS动机模型的设计应用
《义务教育教学课程标准》在课程标准中指出:“了解数学的价值,提高学习数学的兴趣,增强学好数学的信心,养成良好的学习习惯,具有初步的创新意识和实事求是的科学态度”.ARCS动机模型的目的和课程标准目标是吻合的.笔者特以苏教版八年级上册第二章“轴对称图形”的习题课为例展开分析和思考.
2.1 注意策略
习题课的引入要怎样才可以做到吸引学生的注意?若设置的情景简单,门槛低,这样大家容易参与.可以借助视频、问题、实验操作等多种形式,这样可以使抽象的内容具体化,复杂的内容简单化,解题内容活动化,激发学生的求知欲,
环节1 实验操作引起注意
动手操作请你利用提前准备好的长方形纸片进行折叠,你可以得到哪些图形?
设计意图“低起点”的动手折纸,对于学困生,通过直观的“做”,获得心理感知经验,唤醒对数学认知的自觉追求,对于学优生而言,提出能引起思维的半开放问题,让他们在发现和提出问题中,激发求知欲,让每一位学生都能参与课堂活动.
2.2 相关性策略
在学生的注意力被唤醒之后,教师应该将其学习动机继续保持下去,这就需要“相关性策略”,一切教学手段和方法都应该符合学生的认知规律,以学生已掌握的知识为基础,精心设计形式多样、难度适宜的探究活动,通过对原有知识的迁移,从而解决新的问题.此环节从原来“折”的基础上,改变活动为“画”图形,“说”发现,“证”结论,这样的变化让学生感知在折纸过程中数学无处不在,维持学生的学习动机,
环节2 建立相关引发诉求
活动2 请用笔将你的折痕画出来,并给每个顶点标上字母,写出你的发现,
问题1你来说说你是怎么折叠的?通过折叠你可以得到什么?
追问1借助图1你能不能折出等腰三角形?
可以折出多少个?只需要满足什么条件?
追问2 ADCF的形状?怎样证明?
设计意图活动2从“折”到“画”,不断地增加、提高“识”:重叠的角和边都是相等的,折紙的本质就是构造轴对称图形,这样的设置也给学生提供了更多的表现机会,维持学生的学习热情.问题1的设置与学生生活经验关联,可以让所有的学生都能表达出自己不同的想法,克服学生的畏难心理,进一步激发学生的学习动机.追问1、2的解决将与学生所学习的“垂直平分线的性质”“角平分线的定义”相关联,从而总结由“垂直平分线”“角平分线+平行”联想到等腰三角形,学生在实验操作的过程中,清晰、直观地看到各种情况的演变,培养其知识对接能力,激发学生更深层次的学习诉求.
2.3自信策略
2011年新课标中对学生的情感态度提出:“感受成功的快乐,体验独自克服困难、解决数学问题的过程,有克服困难的勇气,具备学好数学的信心”,教学中的“自信”策略可以是:教师肯定学生的提问和质疑、赞扬学生的发言和见解、重视学生的探究方法.本节习题课给学生提供这样一个空间:让学生通过折叠等腰三角形这一根主线,把这一章所学内容全部串联起来,在这个过程中,学生既利用已有知识解决了问题,也对本章进行了梳理.在理清本章知识脉络的同时增强学生学习的自信,从而体验成功的快乐,
环节3问题引导增强自信
活动3在学生的折叠作品中选出两个具有代表性的成果,呈现折叠前后的完整图形,
问题2图3是沿着长方形对角线进行折叠,观察图形,你有什么发现?
追问1 AAEB和AC,ED全等,可以怎样证明?ABED是等腰三角形除了全等还有其他方法可以证明吗? 追问2在图4中,AEFG也是等腰三角形,你可以怎样证明?由此你能得到什么结论?
问题3刚刚利用折叠我们得到了一般的等腰三角形,你能折叠出等边三角形吗?
追问1说说你是怎样想到这样折叠的?请你证明你所折叠是等边三角形,
呈现学生两种不同的折叠方法:
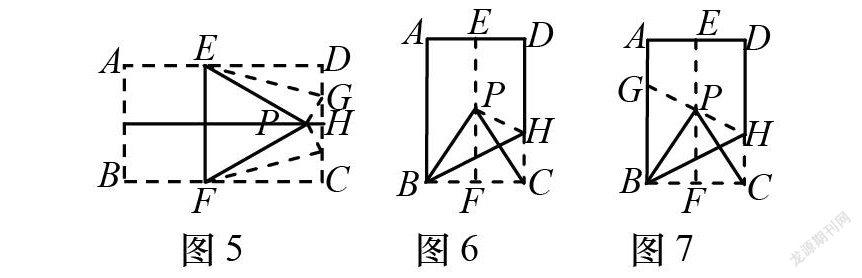
设计意图问题2的设置是建立在学生自己“做”的基础上提出的,教师引导学生提出接下来要探究的主题,学生对自己提出的问题去解决的动机大于教师.在经历追问1后学生熟悉教师的教学“套路”:发现等腰三角形.理论证明,这种熟悉无形之中为学生增加自信,追问2更让学生发现到从特殊(折痕为长方形对角线)到一般(上下两点连线为折痕)的结论:任意沿着长方形对边上下两点连线折叠,重合部分若是三角形,必为等腰三角形,解决这样的问题能够让学生产生挑战更高目标的期望.问题3是一个高难度的挑战,此环节由学生上台分享不同的方法,及时给予激励性评价,培养学生对成功的自信,帮助学生建立其对成功的积极期望.学生的两种不同的方法(如图5.图6)分别是建立在活动2图2的基础上折叠得到的等边三角形,这样可以把复杂的数学问题变得简单,帮助学生树立自信.
4 满足感策略
如何更长时间地保持学生的学习动机?通过及时的反馈和适时的鼓励等方式让学生建立满足感是关键.此环节根据学生已有的数学经验,在让学生亲历问题解决的历程中获得不同层面的最大满足感.
环节4 问题升华获得满足
活动4 我们通过图6已经折出了等边三角形,你能在此基础上折叠得到更大的等边三角形吗?
问题4如图6所示,你可以得到哪些结论?
追问1图6中还有其他的600的角吗?
追问2如图7,怎样说明AGBH是更大的等边三角形?
设计意图活动4的设计是建立在刚才的等边三角形基础上再次通过动手“做”获得更高的目标.而这个环节中设计的4个问题由低到高,这就使得不同层次的学生都能“做”有所获;就问题导向来说,开放与定向同时并存,一步步向目标靠近,问题4让学生在回答的过程中发现“∠GBH= ∠PBH=∠HBC= 30°”.
进而发现可以通过折叠将一个直角三等分,学生在此过程中获得了目标以外的惊喜,追问1指向明确,直达问题的核心,在此过程中要让学生充分表达自己的见解來获得满足,要对学生充分肯定,使学生对自己的成就产生满足感,追问2从理论上验证学生操作的正确性,这样的研究性问题,让学生在克服困难中获得成功的内部体验.
3 教学反思
在本课的教学设计中,以“折纸”引入,符合学生的“最近发展区”,“低起点”的动手操作,唤醒学困生的无意注意的感知行为;通过“画”对称轴,引出折纸的本质——垂直平分线和角平分线,关联学生所学知识和认知经验;折纸由“线”到“形”的转变,由“特殊到一般再到特殊”的完成,完全依赖于学生的动手操作,维持了学生的学习信心;最后在折出等边三角形的图形中发现和探究出更大的等边三角形,让学生获得学习的满足感.
课程标准提出:“教师在教学活动中应该思考:如何引导学生积极参与教学过程?如何组织学生探索?如何使学生愿意学,喜欢学,对数学感兴趣?”ARCS动机设计模型恰恰为此提供了一条有效的思路,学生化变被动接受为主动探索,在活动探究过程中培养学生的求知欲和对数学的兴趣,
值得思考的是:ARCS动机模型是否适用于所有的数学课?笔者认为ARCS动机设计模型的使用在具体的教学中还需要考虑教学的具体内容、学生学情和成长环境,教师更应该精心选择素材,在教学实践中将该模型应用地恰到好处,真正发挥教师的主导地位,学生的主体地位.
参考文献
[1]孙朝仁.ARCS模型对初中段数学实验设计的启示[J].数学通报,2016 (10):11
[2]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012(本文系南京市教育科学研究“十三五”规划课题“基于ARCS模型的初中数学习题教学策略研究”(课题编号:L/2018/182)的阶段性研究成果之一)

