舰炮打击目标优选新方法研究*

解维河 孙卫国 孙东彦

（1.海军大连舰艇学院导弹与舰炮系 大连 116018）（2.中国人民解放军91040部队 青岛 266000）

1 引言

舰炮在作战中承担的作战任务具有多样性，承担着打击不同目标的使命。在舰炮作战使用中，优选打击目标是决定其任务能否完成的关键，也是指挥员在作战中决策的关键要素，尤其是当战场出现新的威胁目标时，如何根据目标特征准确、快速确定目标的威胁等级排序是作战使用的关键难题，目标等级排序和优选影响因素很多，具有很多不确定性随机因素［1～2］。通过将勾股模糊集和基于正弦函数的直觉模糊集相似度相结合，提出基于余弦函数的勾股模糊集相似度，并引入四种勾股模糊相似度测量公式，将此新方法应用到舰炮打击目标优选决策中，能够根据不同等级目标特征进行威胁判断打击优选，尤其是对战场上出现的新的目标，不需要对所有目标因素重新排序，根据新目标出现特征确定其客观指标隶属度，快速计算出目标威胁顺序，便于指挥员迅速决策，为舰炮打击目标决策提供一种全新的方法。

2 预备知识

2013年以来，Yager等学者在直觉模糊集［3］的基础上提出了勾股模糊集［4～5］（Pythagorean fuzzy sets）。勾股模糊集将隶属函数区域从三角形扩大成四分之一圆，并且延续了直觉模糊集的优势，在处理决策问题中更有适应性和灵活性［6～7］。2018年杨勇等利用正弦函数建立了直觉模糊集的相似度测量［8］，并通过具体实例与之前的相似度测量公式进行了比较，收到了更好的效果。

设U是初始论域，P（U）表示U的幂集，序对（U，E）为软论域，IFS（X）和PFS（U）分别表示X和U上的所有直觉模糊子集、和勾股模糊子集。

定义 1［6～7］设U=｛x1，x2，…，xn｝为给定的集合，则U上的勾股模糊集P定义如下：

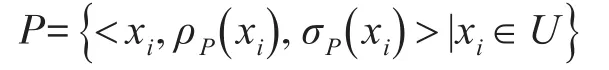
其中ρP(xi)和σP(xi)分别表示元素xi属于集合P的隶属度和非隶属度。二元组（ρP(xi)，σP(xi)）被称为勾股模糊数（简记为PFN），其中ρP(xi)，σP(xi)∈［0，1］，。另外，为犹豫度。

定义 2［8］设A=｛|＜x，μA(x)，νA(x)＞x∈X｝，

B=＜x，μB(x)，νB(x)＞|x∈X｝为论域X上的两个直觉模糊集，S为一个映射：IFN（U）×IFN（U）→［0，1］，如果它满足下列条件：

1）S（A，B）=1⇔A=B；

2）S（A，B）=S（B，A）；

3）若A⊆B⊆C，有S（A，C）≤S（A，B），S（A，C）≤S（B，C），则称S（A，B）为直觉模糊集A和B之间的相似度。

3 基于余弦勾股模糊集相识度评估聚类新模型

由于勾股模糊集与直觉模糊集结构基本一致，接下来就按直觉模糊相似度和正弦相似度测量逐一类似地给出勾股模糊集的同样定义。

定义3设A=｛＜x，ρA(x)，σA(x)＞|x∈U｝，B=＜x，ρB(x)，σB(x)＞|x∈U｝为论域U上的两个勾股模糊集，S为一个映射：PFN（U）×PFN（U）→［0，1］，如果它满足下列条件：

1）0≤S（A，B）≤1；

2）S（A，B）=1⇔A=B；

3）S（A，B）=S（B，A）；

4）若A⊆B⊆C，有S（A，C）≤S（A，B），S（A，C）≤S（B，C），则称S（A，B）为勾股模糊集A和B之间的相似度。

定理1设A和B为论域U=｛x1，x2，…，xn｝上的两个勾股模糊集，则分别定义两个余弦相似度测量公式CS1（A，B）和CS2（A，B），具体如下：

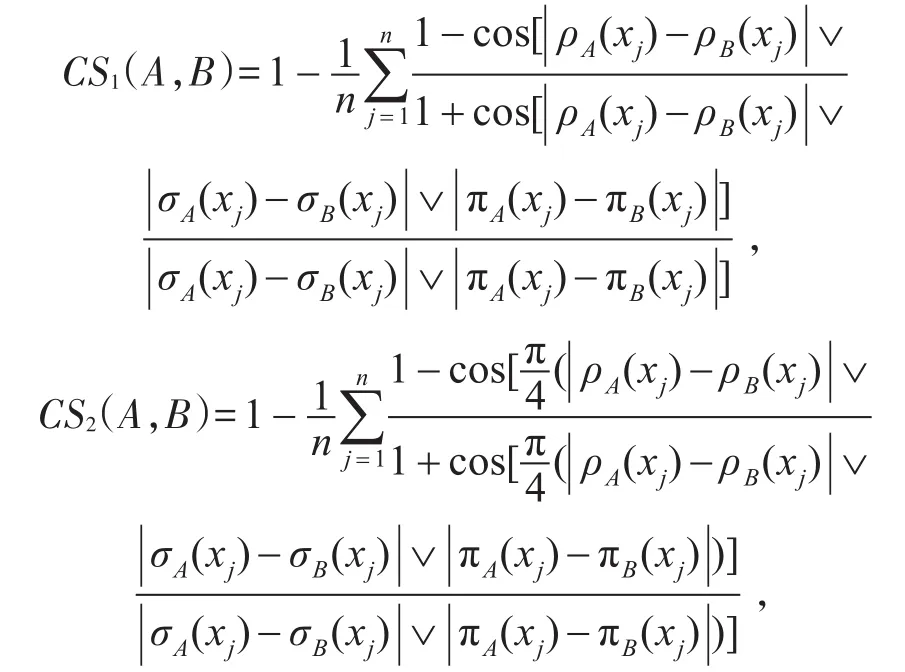
则CS1（A，B）和CS2（A，B）均为A和B之间的相似度。

定理2设A和B为论域U=｛x1，x2，…，xn｝上的两个勾股模糊集，则分别定义两个加权余弦相似度测量公式CS1（A，B）和CS2（A，B），具体如下：

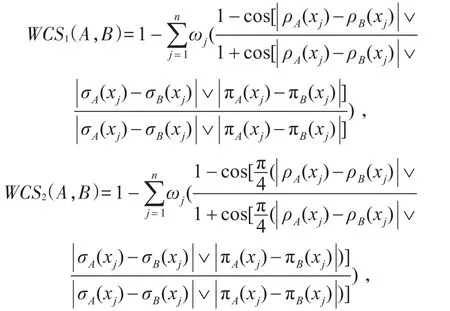
4 基于余弦勾股模糊集相识度的舰炮射击目标优选

舰炮在打击目标选取时，考虑的因素有很多，一般主要考虑五大因素：任务一致程度、目标的重要性、目标威胁程度、目标易损性和信息可靠性。五个因素的的影响程度可以由军事专家进行评判，也可以通过探测到的目标特性，根据既定规则计算综合评判量化分数。我们根据典型的作战态势下战场中出现五个典型威胁目标研究利用基于余弦函数的勾股模糊集相似度方法计算打击目标威胁排序方法［11，13］。其步骤为：1）确定战场目标影响因素的五个方面的综合得分；2）计算隶属函数和勾股模糊集；3）确定权重、得出威胁评估方案；4）计算新目标勾股模糊集；5）确定新目标威胁评估顺序。

以战场出现的五个典型目标的特征因素研究基于基于余弦勾股模糊集相识度的舰炮打击目标威胁判断方法。

4.1 计算现有目标隶属函数、勾股模糊集

确定舰炮打击目标的五个主要因素［9］（一致程度（（x1）、重要性（x2）、威胁度（x3）、易损度（x4）、可信度x5），对五个目标进行五个因素评判得分，具体详见表1。

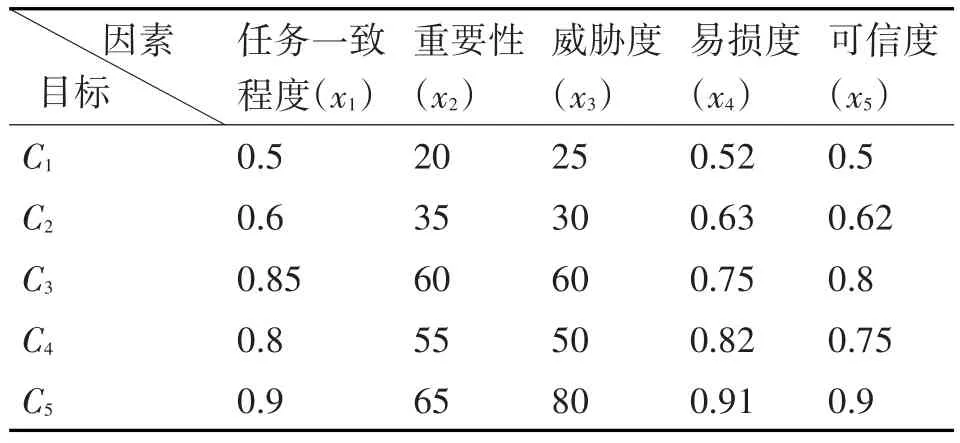
表1 五个打击目标分别在五个方面的综合得分情况

根据上面打分结果计算五个打击目标分别对五个因素的隶属函数：按照确定五个因素下五个打击目标评分的分值从小到大进行排序并赋予序号，然后用序号除以5来计算属于的隶属度ρC(x)，不属于的隶属度σC(x)可以在内凭经验选择，从而分别确定五个打击目标对应的隶属函数值，从而得到对应的五个勾股模糊集的隶属函数数据详见表2。

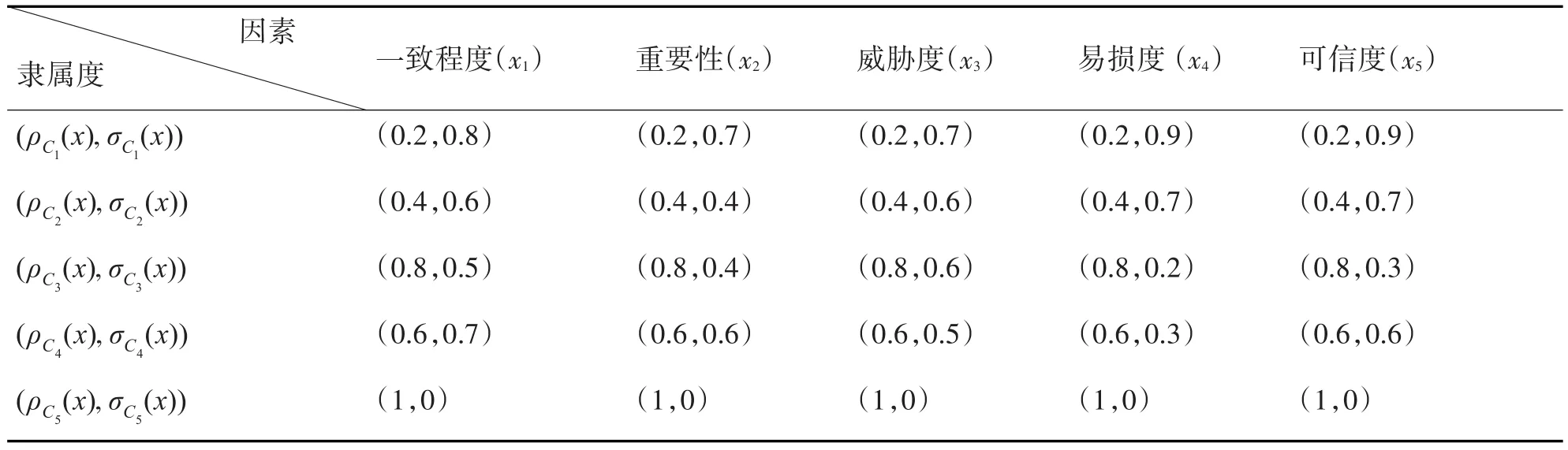
表2 五个打击目标分别在五个方面的隶属函数的数值

4.2 确定权重、得出威胁评估方案

假设五个方面的权重为ω=(ω1，ω2，ω3，ω4，ω5)=（0.4，0.2，0.1，0.1，0.2）。

五个打击目标分别在五个影响因素方面的模糊评估值按照下面公式来计算。

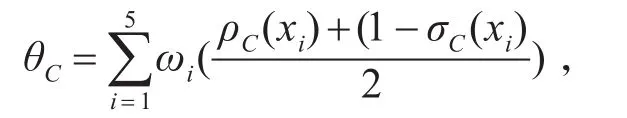
4.3 计算新目标勾股模糊集

按上面的计算方法和标准，根据新出现的目标B的特征因素，给出新打击目标（B）的勾股模糊集隶属函数，得到勾股模糊集=｛＜x1，（0.5，0.7））＞，＜x2，（0.5，0.6）＞，＜x3，（0.5，0.6）＞，＜x4，（0.7，0.5）＞，＜x5，（0.7，0.6）＞｝。

4.4 确定新目标威胁评估顺序

将新打击目标（B）与已经排好顺序的五个打击目标进行比较评估。实质上就是进行勾股模糊集之间的相似度计算，确定它与哪个打击目标的相似度高，那么打击顺序就与其相差不大。

利用距离公式WCS1（A，B）开始计算：假设权重为ω1=0.4，ω2=0.2，ω3=0.1，ω4=0.1，ω5=0.2，则

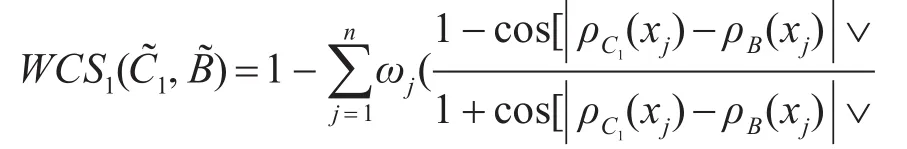
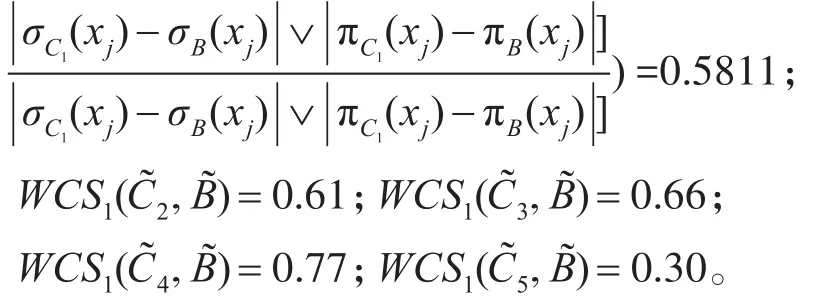
综上可知，B与C4最接近，所以通过比对量化可知五个打击目标和一个新打击目标的先后顺序为C5，C3，C4，B，C2和C1。

此计算方法在不需要重新计算原有目标因素确定打击顺序的基础上对新目标进行威胁评估，能使复杂的问题简单化，减少决策评判时间，尤其是在需要指挥员进行人为决策因素过程中效率更高。

5 结语

舰炮作战使用中打击目标威胁判断是决定作战全局的关键问题，需要从目标状态因素和指挥员决策因素多方面进行研究。本文将基于勾股模糊集这一新理论研究出来的基于余弦函数的勾股模糊集相似度中的一种加权测量公式新方法，应用于舰炮作战使用目标威胁判断决策中，提供了多目标威胁评估和在既定评估方案基础上出现新目标的决策优化方法，丰富了舰炮打击目标威胁评判优化理论，具有很强的实用价值。