优化课堂生成 促进深度学习

福建省石狮市石光中学 (362700) 邱育群

课堂教学是师生之间平等对话、思想碰撞、精神相遇的过程，是共享彼此的思考与经验的过程，是教师依据课堂的实际情况进行重组、调整，以促进课堂有效生成的过程[1].课堂生成性资源，是教学预设的升华，是促进学生深度学习的重要载体.然而，在高中课堂教学中，囿于课时的限制，很多教师常常满足于完成课前的预设方案，而忽视“生成性”教学，直抛概念，奉送结论，隔断了学生概念、结论产生过程的体验，对课堂上生成的资源往往视而不见或轻描淡写.这样看似节省了教学时间，实际上造成了学生思维成长中关键环节的缺失，为后续阶段的数学学习埋下了隐患.因此，在数学课堂教学中，教师应恰时恰点地营造良好的学习环境，智慧地处理好预设和生成的关系，为学生的“动态生成”预留出时间与空间，引领他们自主参与、平等对话，让学生在体验与感悟知识的“再创造”、“再发展”中实现深度学习，提升数学核心素养.

1 创设“情境”，在导问中引领生成

为了让有效生成真正发生，教师应优化情境创设，留给学生充分思考的时间．引发学生在“收放自如”的情境中感知、体验，增强学习的内驱力，促进思维的发展.因此教师应以教材为载体，根据学情精心创设问题情境，激发学生的认知冲突与参与学习活动的热情，诱发学生的探究欲望，让学生在有效的情境中自由思考与讨论, 并给予恰当的引导，使学习能力在经历数学化的过程中获得提升，从而促进课堂生成.

案例1“指数函数及其性质”教学片断

情境1：给我一个支点，我能把地球撬起来.给我一张纸，我比珠穆朗玛峰还要高.把一张厚度为0.1mm的纸对折30次后，总厚度多少？

生1：总厚度y=0.0001×230=107374.1824(m).

师：107374.1824>8844.34，因此纸经过30次对折，厚度超过了珠穆朗玛峰的高度.若对折x次后，总厚度为原来y倍，该怎样描述y与x之间的关系？

生2：y=2x(x∈N*).

情境2：“一尺之棰，日取其半，万世不竭.”将长为一尺的木棰截取x次后,木棰的剩余的长度y是多少？

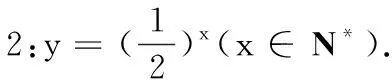
生3：都为幂的形式，指数是自变量，底为常数.

师：对于这一类函数，可以再举一些例子吗？

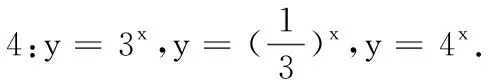
师：是否可以写出这些函数的一般形式？

生5：y=ax.

师：在函数y=ax中，若底数a取不同的实数，就可以得到不同的函数.那么，a的取值范围需要满足什么要求呢？

生7：a不能等于1，若a=1，y=1x是一个常数.

师：很好！为了方便研究，规定底数a>0且a≠1，这就是我们要学习的一种新的函数——指数函数.同学们能给出这个新函数的定义吗？

创设“问题情境”旨在提供给学生学习的背景，使学生产生“欲达彼岸”的求知欲望，引发他们主动参与学习的热情.案例1对教材进行二次开发，创设自然流畅、贴近学生生活、直抵问题本质的情境，激发了学生探究的热情，驱动他们在问题情境中主动探究.学生通过深度思考，抽象出新函数的特征，催生指数函数的概念.

2 善待“偏差”，在反思中孕育生成

学生对于所学的数学知识，既要有一个理解和掌握的过程，也需要有一个总结与反思的过程.波利亚说过：领会方法的最佳时机是解题回顾，它是解题过程的进一步深化，是一个非常重要但很容易被忽略的环节[2].因此在解题教学中，教师应尊重学生自由参与的主动权，因势利导，引导学生养成“回头看”的习惯，通过反思让学生在讨论、辩析的过程中修正错误，厘清问题的来龙去脉，完善认知结构，促进深度学习.

出示问题后，教师先让学生自己思考.学生中出现了两种较典型的错误解法：

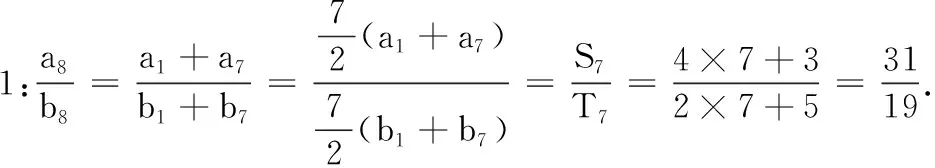
教师没有轻易对以上解法进行表态，而是推波助澜，引领学生反思：

反思一：上面两种方法对吗?

一部分学生认为以上两种方法都正确，另一部分学生认为解法一不正确，解法二是对的，

生2：我认为解法二是对的，以前我们遇到比例问题，往往采用设比例的手段.

教师对这个能够运用“类比”的学生给予了肯定.

师：生2能运用类比推理，值得肯定.那么方法2是否有问题呢？

为了使学生的思维向深度发展，教师进一步让学生反思：

反思二：本题的结论能推广到一般情况吗？

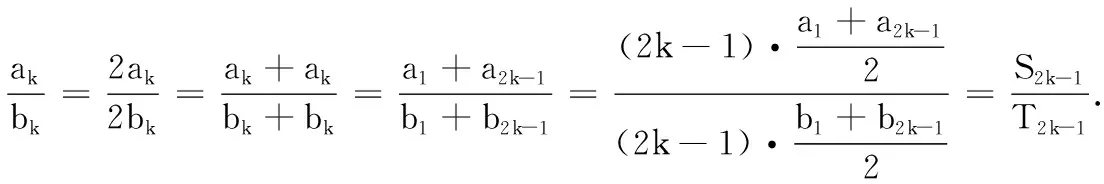
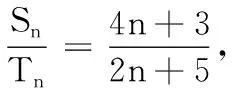
经过反思，学生得到了以下两种方法：

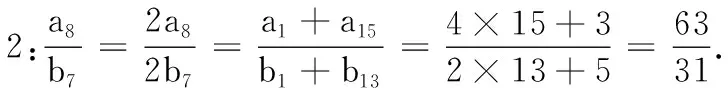
大家肯定了方法1，并认为方法2没道理，应该不正确，但很奇怪两种方法的答案一样.

师：生4运用了类比推理的思想，大家一起来验证一下.

学生跃跃欲试，又推导出了一般结论.

教师有意识地引导学生对所完成的思维过程进行再检查、再回顾，有利于克服知识理解上的偏差，深化学生对数学的认知；有利于梳理数学问题的方法与理论之间的逻辑联系,提升学生的思维监控能力，提高思维的深刻性，使学习发挥“连锁反应”效应，达到解一题，通一类的功效.

3 捕捉“亮点”，在探究中创造生成

在平时的课堂教学中，很多教师往往满足于完成预设的教学内容，而忽略了学生的学习体验.数学课堂是动态多变的，在教学过程中，不可避免地会碰到不在预设范围内的新信息、新思考.在这一过程中，往往会收获一些预设之外的生成.教师应尊重学生，将提出问题的权利还给学生，为他们造就勇于发表意见的平台，并及时捕捉学生思维的“闪光点”，适时调整教学过程，让数学课堂因“动态生成”而精彩！

案例3“圆锥曲线复习课”教学片断

学生完成了上述问题之后，教师又提出问题：

问题二：能否将问题一一般化？

学生经过探究，得到了如下结论：

当教师准备进入另一个教学环节时，一个学生举手提问.

师：说一说你的想法.

生1：将椭圆与圆类比，圆心变为两个焦点F1,F2，我猜测∠F1PF2的平分线与C的切线垂直.

师：如果猜想成立，椭圆的切线与∠F1PF2的外角平分线是什么关系？

生2：由于∠F1PF2的角平分线与它的外角平分线垂直，因此∠F1PF2外角平分线即为C的切线，这样切线l与PF1、PF2所成的角相等.

这些“好念头”激发了同学们的探究欲望，经过验证，得出了下列结论：

师：问题一能利用此结论解决吗？

图1

师：请同学们一起研究一下上述解答过程，看还能不能发现新的结论？

推论3 从椭圆的两焦点向椭圆的任意一条切线引垂线段，则这两条垂线段的长的积是一个常数.

图2

问题三：过圆外一点作圆的两条切线，该点和圆心的连线是这两条切线夹角的平分线.椭圆有相似的结论吗？

学生跃跃欲试，通过探究，又获得以下结论：

图3

证明：如图3，作点F1关于PA的对称点F11，由推论2可知，F11,A,F2三点共线，因此|F2F11|=|AF2|+|AF11|=|AF2|+|AF1|=2a.同理，作点F2关于PB的对称点F22，可得|F1F22|=2a，因为|PF1|=|PF11|，|PF2|=|PF22|，所以△PF1F22≌△PF11F2，因此∠F22F1P=∠F2F11P，又∠PF1A=∠F2F11P，所以∠AF1P=∠PF1B，即PF1平分∠AF1B；同理，PF2平分∠AF2B.

在平时教学中，笔者发现不少教师总是习惯于“牵着学生的鼻子走”，面面俱到地讲解，生怕有什么地方遗漏了.大部分学生忙着“被动接受”，没有自己的思考时间，没有对问题深度理解，更谈不上融会贯通了.数学课堂应适当“放手”，引导学生自由思考、交流，让学生经历困惑、比较分析、感悟与提升的过程，看似耽误了课堂进度，实际上学生的关键能力在体验与思考中获得了升华，这样，通过一个问题的解决，提炼出问题的一般规律，让学生掌握了一类问题的解法[3].案例3以问题为载体,留出充分的时间让学生思考、探索.课堂中学生提出的问题、出现的“亮点”资源，是他们灵感的迸发、思维的顿悟.教师适时引导，置“课堂生成”于教学常态，使之成为引导学生深度思考的契机.在教师睿智的引领下，架起了师生合作探究的平台，学生兴致高昂，在探究中体会到了数学知识之间的逻辑联系，并引发了对一般规律探究的热情，培养了创造性思维.这种生成性课堂教学的优势往往超越了教师的讲授，达到了深度学习的目的.

总之，数学课堂教学是一个复杂的、丰富的、不断变化的过程，是预设与生成和谐作用的结果.在精心预设的前提下，教师应充分利用课堂即时生成的有价值的资源，引导学生主体参与丰富多彩的探究活动，并为课堂的动态生成智慧“接生”，才能打造出充满灵动的高效课堂，引导学生在深度学习中不断提升数学核心素养.