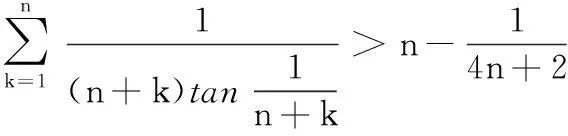数学解题中转化思想的运用——以二道高考模拟题教学为例

淮北师范大学数学科学学院 (235000) 司隽男 张 杰

化归与转化思想是将复杂或陌生的问题A通过某种方法，转化为有解决思路的或熟悉的问题B，通过解决问题B进而解决问题A的思想方法．在数学解题的过程中，转化思想是至关重要的，同时这也是实现数学变换的必要思想．数学高考与模拟考中的导数压轴题往往具有较强的综合性，可以很好的考察学生化归与转化思想，分析与解决问题的能力以及逻辑推理、数学运算等核心素养，而这些题目常常需要进行数学变换才能顺利解决．所以教师在解题教学中应当重视渗透化归与转化思想，鼓励学生主动思考，帮助学生拓宽解题的思路．

为了说明如何运用化归与转化思想以简驭繁，解决导数不等式证明题，先从2021年广州市普通高中毕业班综合测试(二)中的一道压轴题说起．

例1 (2021广州二模22)已知函数f(x)=ln(x+1)+a(x-1)2(a>0)．

(1)讨论函数f(x)的单调性；

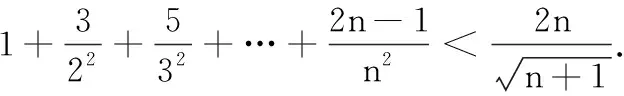
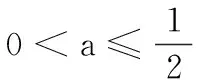
对于问题(2)，由于不等号左边是累加形式，因此可以对原式进行转化，再运用放缩法证明该不等式．现将解题过程呈现如下：

由上述解答过程，可以感受到转化思想能够化繁为简，有助于证明不等式．但是具体如何转化，从而能够利用已有的知识来证明不等式，对于很多学生而言心余力绌．因此在教学过程中不能直接向学生展示题目的解法，而应该启发学生思考，帮助学生理解其中的数学思想，以便能够举一反三、触类旁通．下面展示传授这一解题方法的教学设计：

生1：求数列的前n项和．

师：很好，那我们是否可以考虑将不等号的左边看作是数列的前n项和，尝试运用解决数列问题的常用方法进行证明？

师：既然①式对任意n∈N*都成立，所以有a1+a2+…+an-1

生3：an

师：③式中的“<”一定成立吗？

生4：不一定成立，例如5<2，3<1，但是2>1．

师：③式与①式有怎样的关系呢？

生5：①式成立时，③式不一定成立，但是③式成立时，①式一定成立．

师：很好，那么对于④式该如何证明呢？

至此，此题的解答思路已经很清晰了，后续的证明学生可以独立完成，这里不再赘述．通过上述的解答过程，可以看出在化归与转化思想的指引下可以较简便的解决这类导数不等式证明题．

例2 已知定义在R上的函数f(x)=x2+acosx+(a-2)e-x,a∈R．(其中常数e是自然对数的底数，e=2.71828…)

(1)当a=2时，求f(x)的极值；

(2)(i)若f(x)在[0，π]上单调递增，求实数的取值范围；(ii)当n∈N*时，证明：

这是2021年深圳市高三年级第二次调研考试中的一道压轴题，其中问题(2)中的第(ii)问与例1中的第(2)问比较类似，即不等号左边都是累加的形式．于是仿照例1的解答思路，将问题转化为证明“an>f(n)-f(n-1)”．但本题是否可以继续使用这种解题思路还需要进一步分析．现将本题的解答过程呈现如下：

对于问题(1)，读者通过对函数进行求导并判断其单调性，从而求出f(x)的极值，即当a=2时，f(x)极小值为f(0)=2，无极大值．

通过上述对问题(2)中的第(ii)问的解答可知，遇到证明同类型的题目时不能完全按照“套路”进行，需要具体问题具体分析，根据已知条件对问题进行转化，再进行证明．下面展示解答该题的教学设计：

师：很好，那么④式是否成立呢？

师：既然仿照例1中的方法不能解决此题，那么我们就要转换思路了．请同学们仔细观察题目中的已知条件，有什么发现吗？

生3：题目中并没有出现tan，但是出现了cos，所以不妨考虑将②式中的tan转化为cos，即

师：很好，现在我们可以将这一累加的式子看作是数列的前n项和，想一想在学习数列知识时若遇到这种不等式常采用什么方法来证明呢？

生4：我们通常使用放缩法进行证明，先对每一项进行放缩，再通过累加相消，最终证明不等式成立．

师：那我们不妨尝试使用放缩法，看看是否能够证明本题．

在导数压轴题中证明形如“对任意n∈N*，都有a1+a2+…+an>f(n)”的基本方法：首先判断an>f(n)-f(n-1)是否成立，若成立，则原式得证；若不成立，则需要利用题目中的已知条件对问题进行转化，进而证明该题．

通过上述的解题教学，学生不仅可以明晰何时需要对题目进行转化，而且能够知道如何进行转化，进而能够融会贯通，真正理解解题的思路，这样才是有效的教学．

经过上述的两道高考模拟题的解答容易意识到，在数学解题的过程中，选择何种思路解决问题是十分关键的．而对于导数不等式的证明题，如果不等式中出现了累加的式子，可以考虑对累加部分进行转化，将陌生的问题转化为熟悉的问题，再运用已学的方法进行证明．最终使新知识融入到已有的数学知识结构中去，并在此基础上生长出一些新的想法与感悟，从而在脑海里构建出一个更加完善的知识结构．