例析阿波罗尼斯球的应用

江苏省梅村高级中学 (214112) 王 刚 陶煜瑾

平面上一动点到平面上两定点的距离之比为定值(大于0)，且定值不为1，此时，动点的轨迹为圆，称之为阿波罗尼斯圆.类似的，空间一动点到空间内两定点的距离之比为定值(大于0)，且定值不为1，此时，动点的轨迹为球，称之为阿波罗尼斯球，简称为阿氏球.下面举例说明阿氏球的相关应用.

图1

图2

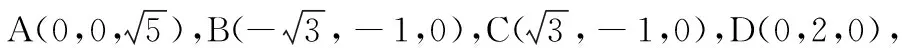
阿氏圆中涉及四个量，即平面内两个定点，平面内动点轨迹方程，动点到两定距离的比值，它们可以知三求一.当我们知道了一个定点，动点的轨迹方程，动点到两定距离的比值可以求出第二个定点，我们发现这两个定点连线通过圆心，并且它们到圆心的距离之积为阿氏圆的半径的平方，我们把这两个点称作是这个阿氏圆的一对反演点.类似的，阿氏球中也涉及四个量，即空间两个定点，空间动点轨迹方程，动点到两定距离的比值，它们可以知三求一.当我们知道了一个定点，动点的轨迹方程，动点到两定距离的比值可以求出第二个定点，我们发现这两个定点连线通过球心，并且它们到球心的距离之积为阿氏球的半径的平方，我们把这两个点称作是这个阿氏球的一对反演点.

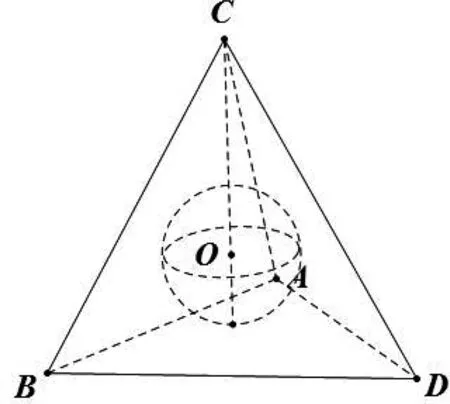
图3

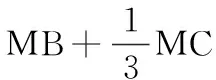
图4

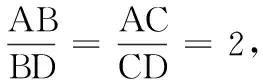
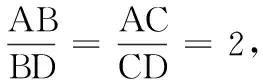
图5