基于线性变换的领导−跟随多智能体系统动态反馈均方一致性控制

郑维 张志明 刘和鑫 张明泉 孙富春

自然界里存在着许多生物聚集的现象,比如候鸟迁徙、鱼群逆流、蚁群迁徙等.通过对自然界各种群集现象的研究以及对现有的网络模型结构的理解,学者们提出了多智能体系统(Multi-agent system,MAS)的概念[1−4].多智能体系统中各智能体之间相互协同合作的基础就是一致性问题.文献[5]给出了多智能体系统一致性问题的系统基础结构,同时对一致性问题提出了标准化的数学表达.多智能体系统领导跟随一致性问题作为一个重要的协同控制问题同样是学者们关注的热点.其领导者不受跟随者影响,且要求跟随者和领导者目标一致.

近年来,对于领导−跟随多智能体一致性控制的研究热度不断增长,并涌现出了大量的研究成果.文献[6]研究了在固定和变换拓扑下领导−跟随多智能体系统协同控制信息的一致性算法.文献[7]针对有向拓扑结构研究了时变的领导−跟随多智能体网络的一致性问题.在领导−跟随多智能体系统中如果减少自主体之间的通信次数,就可以减少网络中的节点之间数据的传递次数和频率,提高系统的收敛速度.文献[8]研究了具有交换拓扑和存在噪声的多自主体系统模型,提出了一种基于领导−跟随多智能体自身以及邻居状态的一致性采样控制协议.文献[9]基于M 矩阵理论进行一致性收敛分析,讨论了采样数据框架下的一阶多智能体系统领导跟随一致性问题.文献[10]研究了一类二阶非线性多智能体系统的领导跟随一致性问题,利用相邻智能体之问的相对信息给出分布式自适应非线性控制率.事实上,领导−跟随多智能体系统常常受到外部因素的影响,例如: 通信时滞和执行器故障,从而使得一致性问题变得更具挑战性.

在许多物理系统中,如通讯及工业控制系统中,由于信息传输速度受限、传输通道拥堵等原因,时滞在网络化多智能体系统中总是不可避免的出现[11].时滞的出现对整体系统的性能影响很大,例如: 系统稳定性、收敛速度、收敛效果等.因此,研究存在时滞的多智能体系统一致性控制问题非常必要.文献[12−14]研究仅含有通信时滞的一致性问题.通信时滞主要指某个智能体与其邻居之间信息传递过程中产生的时间延迟;文献[15−16]研究仅带有输入时滞的系统一致性问题;文献[17]对带有输入时滞及通信时滞的系统进行一致性分析;文献[18−20]对含有常数通信时滞的二阶多智能体系统进行一致性分析,并求得达到一致性的充分条件.文献[21]使用脉冲控制方法研究了具有不确定和随机发生非线性的多智能体系统一致性;文献[22]研究了具有非线性输入项的非线性多智能体系统的领导—跟随一致性,且该分布式控制协议保证系统一致性;文献[23]研究具有时变输入时滞的线性多智能体系统分布式一致性;文献[24]研究具有时变通信时滞的非线性多智能体系统一致性;文献[25−26]基于模型简化法研究多常数时滞的多智能体系统一致性问题,将系统转化为不含时滞的系统.

在实际应用中,智能体自身的能量和通信信道带宽都是有限的[27−28].一般而言,控制任务中的测量、通信和控制协议的更新都是周期性执行的,即周期采样控制方法[29−31].为了保证所有执行点的性能,采样时间常数通常取一个保守值,这通常会造成通信资源和计算资源的浪费,进而造成信息拥堵,引起时滞.从理论研究角度看,时滞系统研究更关注非线性系统和状态时滞.但是,由于复杂控制系统中时滞具有不确定性,时变时滞更具有研究价值.此外,在实际系统中,外部扰动的存在,对实现系统一致性造成了极大的困难,因此考虑外界扰动更具有实际意义.如果所设计的控制器能够有效抑制扰动,那么系统达成一致性的同时就具有了强鲁棒性.与现有的研究结果相比,本文采用系统的H∞性能指标来分析系统的鲁棒性.另外,关于多智能体一致性控制问题的研究,现有研究多集中在固定拓扑或无向拓扑,这就对系统的通信能力提出了极高的要求[32].文献[33−34]研究了具有利普希茨(Lipschitz)非线性动力学的多智能体系统的一致性控制问题.其中,文献[33]假设跟随者之间的拓扑不是强连接和固定的,进而解决智能体的共识跟踪问题.在文献[33]基础上,文献[34]基于采样数据信息对具有Lipschitz 非线性动力学的多智能体系统进行一致性分析,同时采用输入延迟的方法,将得到的采样数据闭环系统重新规划为控制输入具有时变时滞的连续系统,进而实现多智能体一致性控制.

时滞现象广泛地存在各种实际系统中,如生物系统、神经网络系统、自动化系统、通信系统等.此外,控制系统在工作过程中时常发生故障,且不可避免,例如: 执行器故障及控制输入传输故障[15]等.在含有通信拓扑结构的多智能体系统中,由于信息传输速度受限、传输通道拥堵等原因,通信时滞在网络化多智能体系统中总是不可避免的出现.通信时滞主要指某个智能体与其邻居之间信息传递过程中产生的时间延迟,且通信时滞会影响多智能体系统的整体性能,例如: 系统的稳定性和收敛速度等.因此,针对领导−跟随多智能体系统,基于系统的安全因素及更高的可靠性和鲁棒性的需求,设计一个有效的控制策略十分重要.

基于上述研究内容,在切换通信拓扑结构下,本文针对基于半马尔科夫(Markov)跳变的带有通讯时滞和执行器故障的领导−跟随多智能体系统,设计一种新的动态反馈控制策略.根据多智能体系统的均方一致性要求,对系统进行线性变换.同时设计(Lyapunov)函数,对符合Lipschitz 条件的非线性项,利用Lyapunov 函数抑制系统的非线性特性,通过求解相应的线性矩阵不等式(Linear matrix inequality,LMI),证明了多智能体误差系统稳定性,并导出了系统稳定的充分条件,从而实现了领导−跟随多智能体系统的均方一致性控制.设计动态反馈控制器,对误差系统的系统矩阵进行线性化处理,解决由控制器未知增益矩阵引起的非线性问题.该设计方法能够使多智能体系统受到外部扰动时,系统状态以相对较小的振荡快速趋于一致,满足暂态响应性能指标.将实现领导−跟随多智能体系统的均方一致性问题转化为多智能体误差系统的稳定性问题.并利用线性矩阵不等式求解增益矩阵,增强设计控制器的灵活性.最后,仿真结果表明基于线性变换设计的动态反馈控制器策略有良好的控制性能,并且能够提高领导−跟随多智能体系统的动态特性.

1 问题描述

考虑由1 个领导者和N个智能体个体组成的连续时间领导−跟随多智能体系统,其中第i个跟随者的动力学模型为

领导者的动力学模型为

其中,κ ≥0 表示非负标量.

假设 3.每个可能存在的拓扑结构图G(k),其中k∈S,都有一个以领导者为根节点的生成树.

假定拓扑结构之间的变换满足半Markov 切换过程,并将变换拓扑结构表示为如下形式

其中,{rt,t ≥0},G(rt) 为半Markov 过程.

针对本文描述的领导−跟随多智能体系统的动力学模型,基于邻居者信息以及延迟信息,设计如下控制律

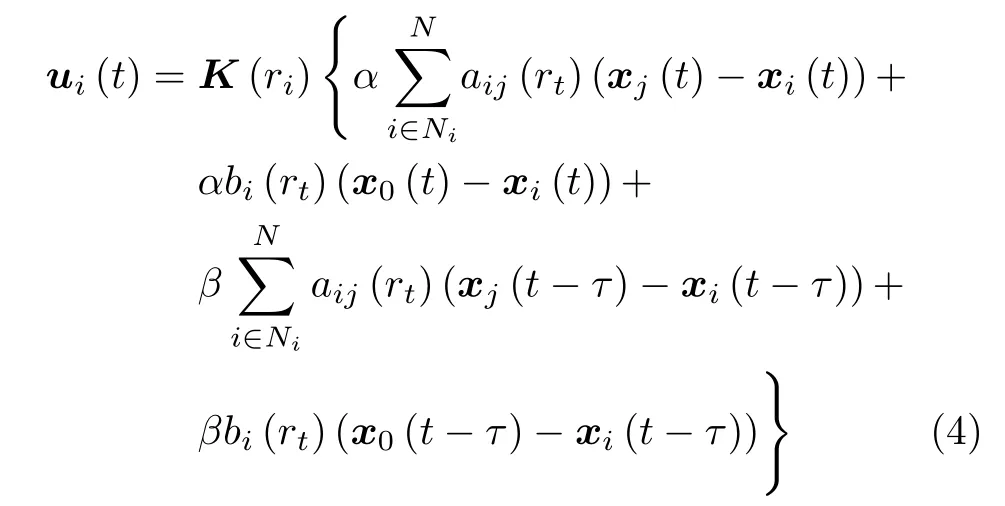
式中,α和β表示当前状态与延迟状态的耦合强度,τ ≥0 表示通信时滞.rt=r(t) 表示系统切换信号,aij(rt) 表示系统切换函数,K(rt) 表示控制器增益矩阵,根据切换信号对控制增益矩阵进行设计.

2 均方一致性控制器设计

针对领导−跟随多智能体系统(1)和(2),定义系统误差变量为

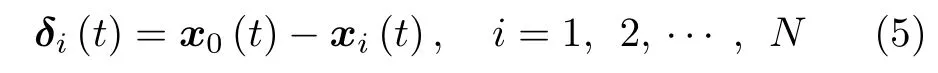
其中,δi(t) 表示系统误差变量,x0(t) 表示领导者状态变量,xi(t) 表示第i个跟随者的状态变量.

对式(5)求导,可得

将式(1)和式(2)代入式(6)中,可得

为了简化式(7),引入中间变量f(δi(t),t)和(t),有

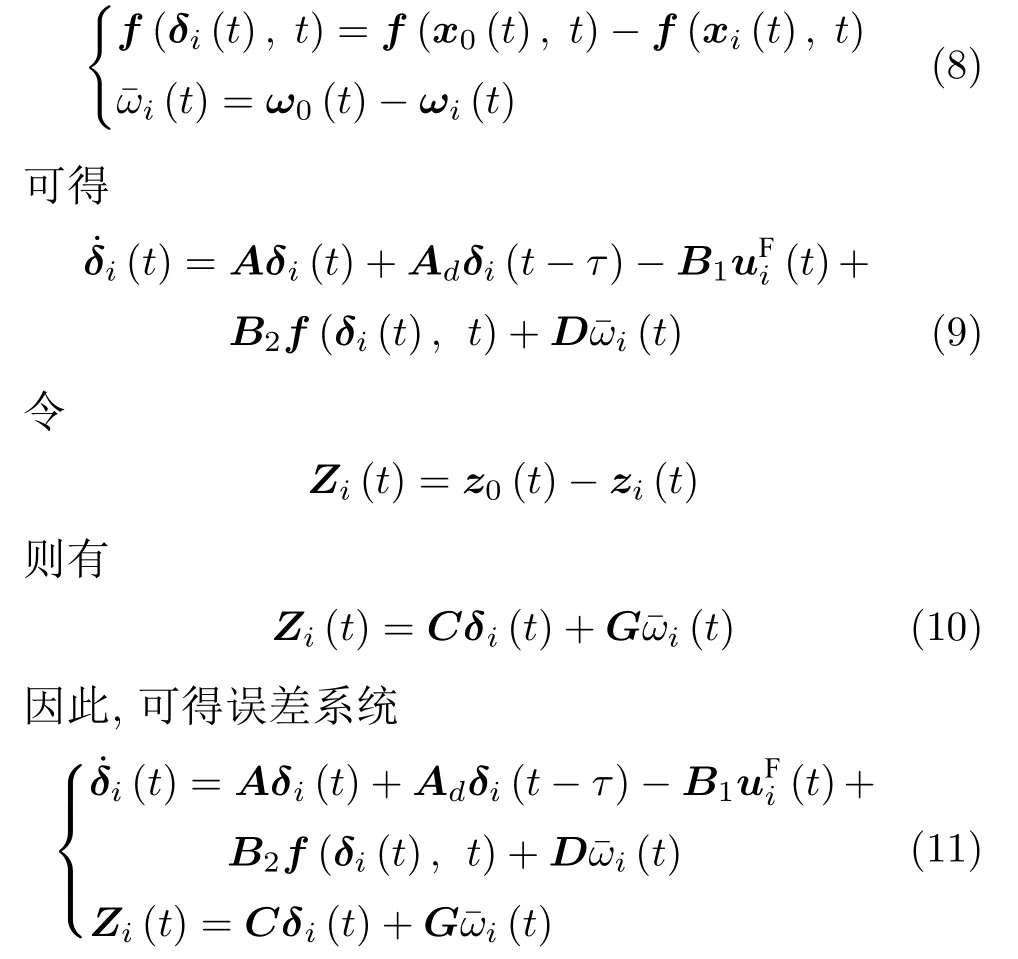
通过上述变换,将多智能体系统单个跟随者与领导者的一致性问题转换为了上述误差系统(11)的稳定性问题.

定义如下向量

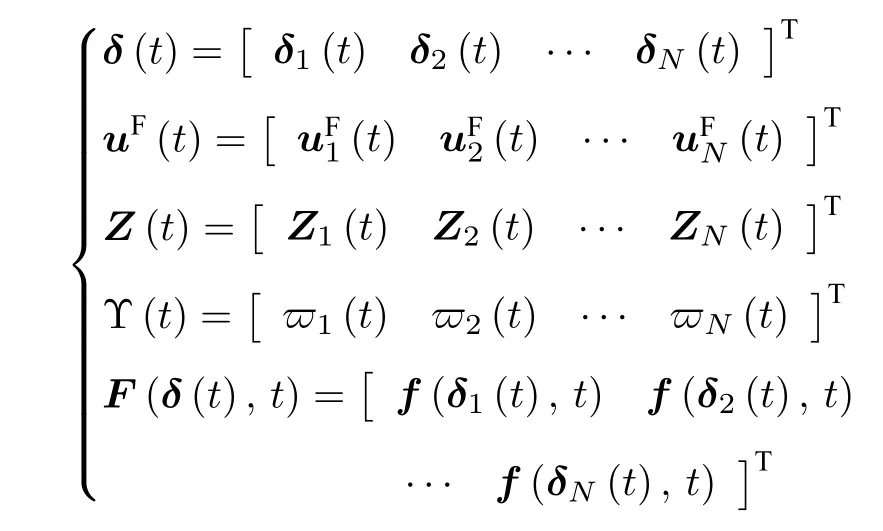
根据克罗内克(Kronecker)积,可得

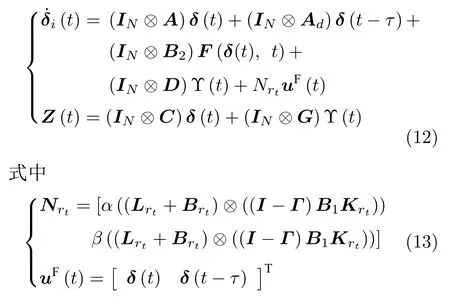
注 1.从式(11)可以看出,通过上述变换,根据Kronecker 积的相关定义以及上述向量,可将单个误差系统转化为误差系统的向量形式,即将领导−跟随多智能体系统(1)和(2)的一致性问题转化为误差系统(12)的稳定性问题.

将δi(t)=x0(t)−xi(t) 代入到系统输入表达式(4)中可得

带有执行器故障的控制输入表达式为

因此,根据多智能体系统拓扑结构图的拉普拉斯(Laplacian)矩阵,Kronecker 积的相关性质和式(13),可得

那么,误差系统(12)的最终形式为

那么,将领导−跟随多智能体系统的一致性问题最终转换为误差系统(16)的稳定性问题.在后续计算中,将rt简写为r.

针对本文提出的问题,给出定义1和引理1 如下,定义1和引理1 将用于系统的稳定性分析.

定义 1[35].对于具有外部扰动的控制系统,且外部扰动为ω(t),在零初始条件下,若系统输出z(t)满足

3 稳定性分析

定理 1.在假设1～3 的条件下,对于给定参数τ >0 ,σ≥0和给定矩阵Γ,若存在正定矩阵Pr >0,r=1,2,···,s,Q>0 以及正定对角阵T >0,使得

那么,在控制器(4)的作用下,多智能体系统能够达到均方一致性,且满足H∞性能指标γ >0.

证明.证明分为两个部分,无外部扰动时的稳定性证明与有外部扰动时的H∞稳定性证明.

首先,令 Υ (t)=0,证明系统稳定性.选取正定Lyapunov 函数为

对式(18)求导,可得

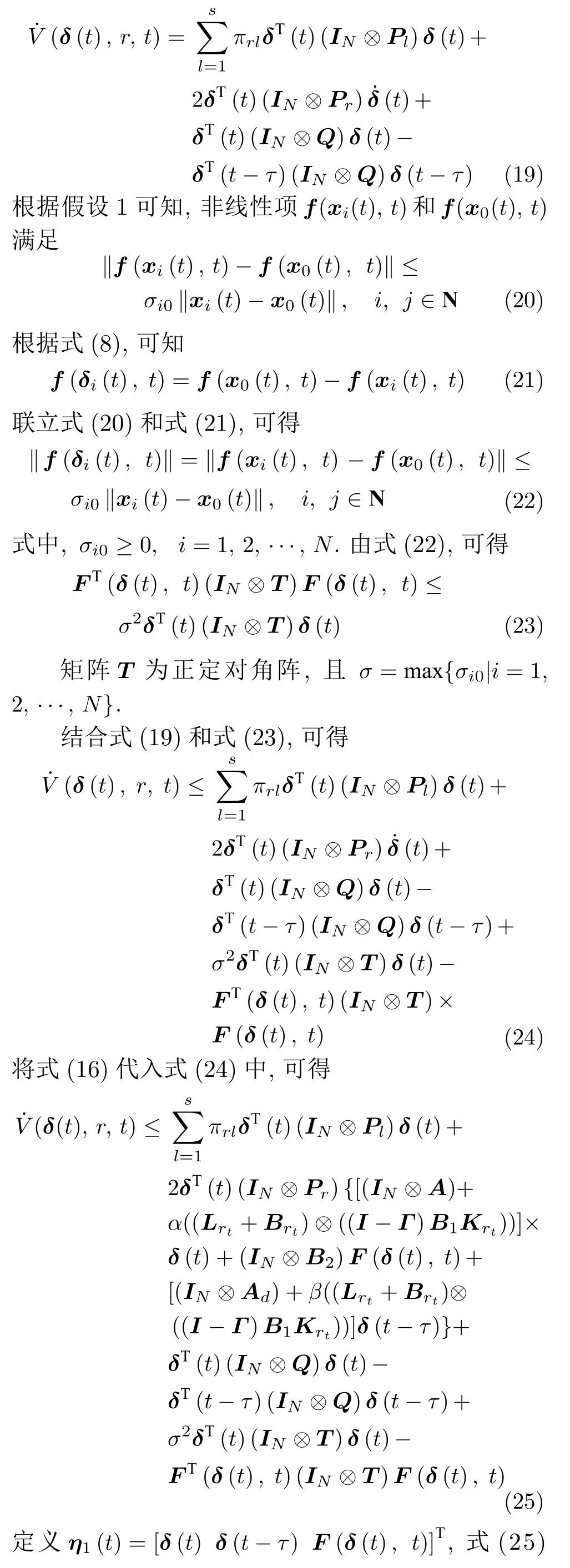
根据引理1 以及式(17),式(26) 中的矩阵Ψr <0,从而保证所选取Lyapunov 函数的导函数为负定.

当 Υ (t)0 时,对系统的H∞性能进行分析.由式(26)和式(16),可得

将式(16)代入式(28)中,根据引理1,可得

因此,由式(16),可得

由Dynkins 公式可得

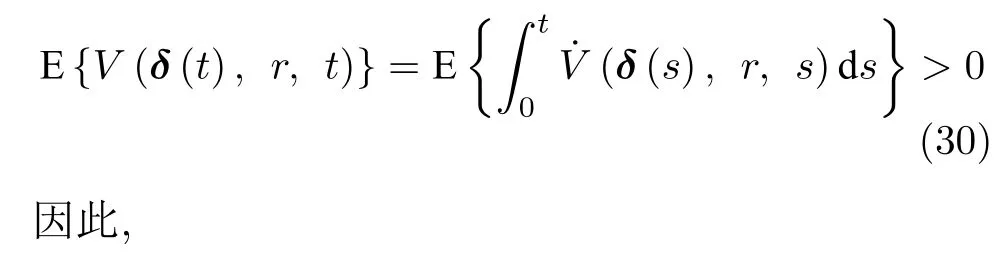
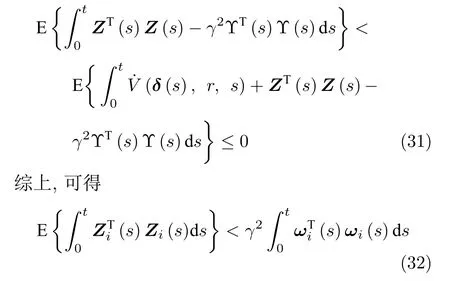
多智能体能够达到一致性,满足H∞性能指标.□

注 2.由于控制器增益矩阵Kr为未知矩阵,因此,定理1 中的矩阵不等式为非线性的,对Kr的求解造成了困难.本文给出使定理1 成立的充分条件,并且满足线性矩阵不等式的要求,从而利用线性矩阵不等式工具箱解得控制器增益矩阵.

定理 2.在假设1～3 的条件下,对于给定参数τ >0,σ ≥0和给定矩阵Γ,若存在矩阵Xr >0,Yr >0,Ur >0和Wr >0,使得

那么,在控制器(4)的作用下,领导−跟随多智能体系统(1)和(2)能够达到均方一致性,并且具有H∞性能指标.其中,控制器增益矩阵Kr=

证明.将式(17)中的矩阵分别左乘、右乘对角阵,将式(34)中的矩阵代入后,可得

利用引理1,可将ζ11中的第2 项展开为Φr中的χ16和χ66两项,因此,式(35)等价于式(33),不等式(33)即为满足线性矩阵不等式要求的矩阵不等式,可通过LMIs 工具箱对其中的未知矩阵求解,从而得到控制器增益矩阵. □

注 4.本文通过定理1和定理2 分析了在切换通信拓扑结构下,带有非线性项、执行器故障和外部扰动的领导−跟随多智能体系统的均方一致性控制问题.针对给出的领导者与跟随者系统模型(1)和(2),通过线性变换,将均方一致性问题转化为领导−跟随误差系统的稳定性问题.降低了系统设计的保守性.对符合Lipschitz 条件的非线性项,利用Lyapunov 函数抑制系统的非线性特性.并利用时变转移概率矩阵设计半Markov 过程来描述通信拓扑的切换过程.基于动态反馈控制和邻近原则,设计动态反馈控制器,对误差系统的系统矩阵进行线性化处理,解决由控制器未知增益矩阵产生的非线性问题.该设计方法能够保证多智能体系统受到外部扰动时,系统状态以相对较小的振荡快速趋于一致,从而满足暂态响应性能指标.

丁柔是周桥的前女友，在众人眼里是女神一般的存在，毕业没多久就成了北漂一族，当年她嫌周桥不够有斗志，坚持了一年异地恋后结束。

4 仿真验证

领导者是一个运动学独立于其他智能体的特殊智能体,它可以对其他的跟踪智能体产生影响,反之通常不成立,故可以在仿真验证中通过控制领导者智能体的运动来完成对多智能体系统最终状态的控制,这样便简化了多智能体系统的控制过程,同时也降低了控制成本.因此,为了验证本文提出方法的有效性,分别给出例1和例2,验证具有1 个领导者和不同数量跟随者的多智能体系统的一致性控制问题.

例 1.考虑由1 个领导者和3 个跟随者组成的领导−跟随多智能体系统,该多智能体系统的通信拓扑结构如图1 所示,即{G1,G2,G3,G4},其中智能体0 表示领导者,智能体1,2,3 表示跟随者.

图1 系统通信拓扑结构Fig.1 The topological structure of system communication

领导者和跟随者的系统参数矩阵给定如下:

假设该系统通信拓扑的切换过程满足半Markov过程,且有4 个不同的拓扑结构,如图1 所示,给定系统转移概率矩阵的变化域如下所示:

系统的其他参数设定为α=3,β=5,τ=0.4,σ=0.1,ξ1=0.4,ξ2=0.6,利用MATLAB 中的LMIs工具箱,求解矩阵不等式(33),可得系统的H∞参数为γ=0.76,控制器增益矩阵为

给定系统的初始状态为

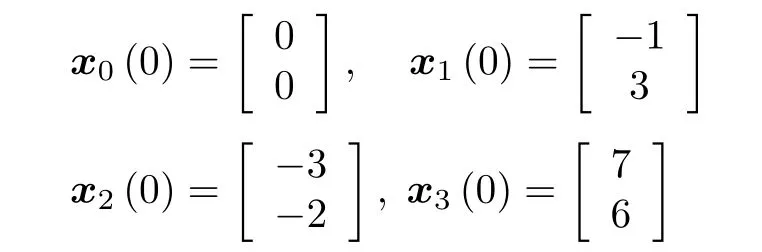
在控制器(4)的作用下,得到系统的状态响应曲线如图2和图3 所示,令系统的误差为e(t)=且误差曲线如图4 所示,系统通信拓扑的半Markov 切换信号如图5 所示.系统的状态响应图表明,3 个跟随者智能体的状态响应曲线,在切换信号的影响下,能够逐渐向领导者智能体状态轨迹靠拢,在4 s 左右达到一致;误差曲线图4 表明,对于领导−跟随多智能体系统(1),在本文设计的一致性控制器的作用下,能够实现一致性控制,并具有较好的鲁棒性.从仿真图4 可以看出,系统误差的过渡过程时间是1.95 s.从图4 的过渡过程时间可以看出,虽然误差响应曲线的纵轴数量级相对较大,但是误差在1.95 s 收敛到0,并保持稳定,体现了系统误差的稳定性能.

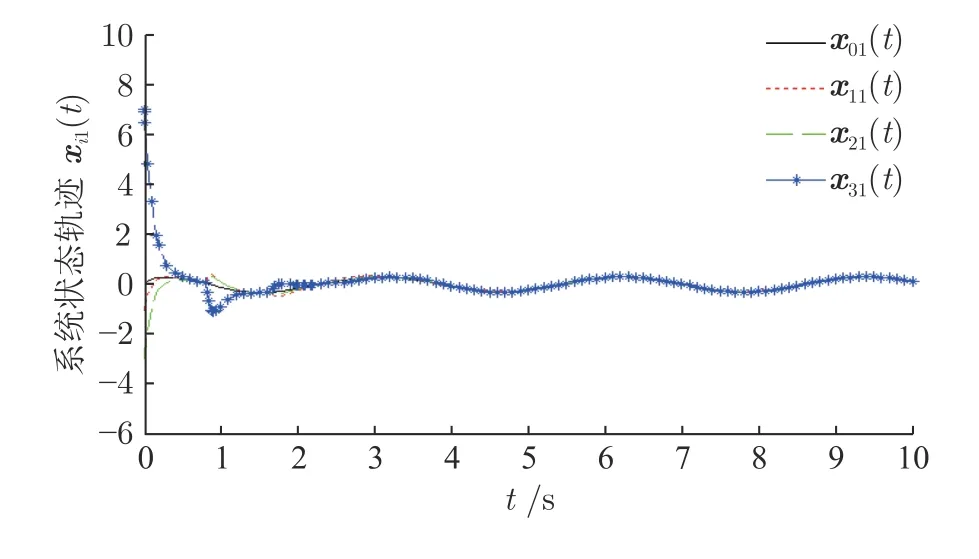
图2 状态变量xi1(t) 响应曲线Fig.2 The response of state variablexi1(t)

图3 状态变量xi2(t) 响应曲线Fig.3 The response of state variablexi2(t)

图4 系统误差e (t) 响应曲线Fig.4 The response of system errore(t)

图5 通信拓扑切换信号Fig.5 The switching signal of communication topology

例 2.考虑由系统模型为(2)的1 个领导者和系统模型为(1)的5 个跟随者组成的领导−跟随多智能体系统,该多智能体的通信拓扑结构如图6所示,即{G1,G2,G3,G4},其中,智能体0 表示领导者,智能体1,2,3,4,5 表示跟随者.

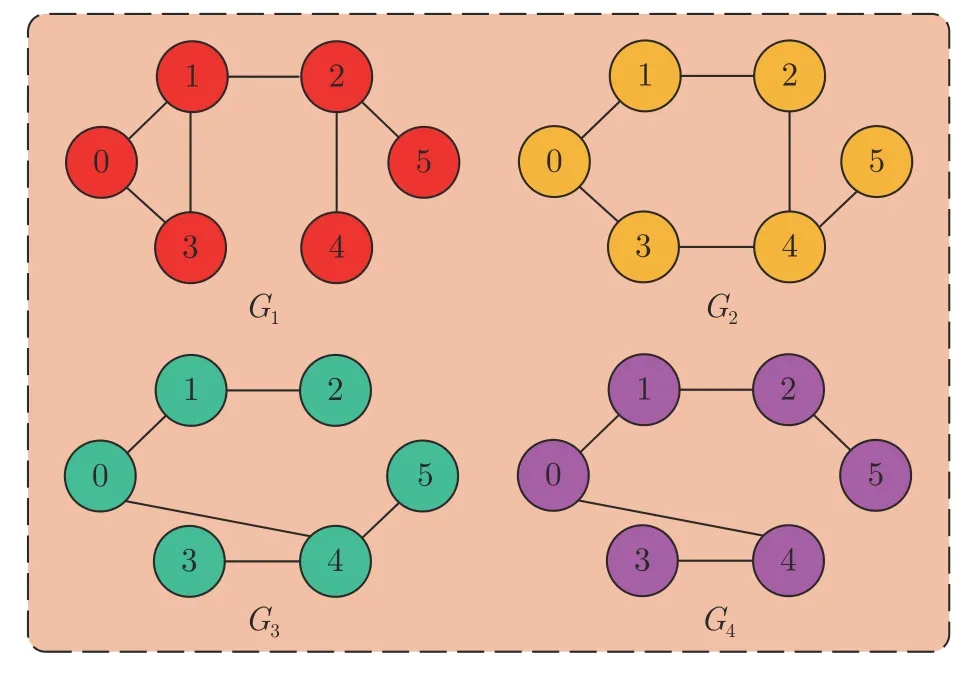
图6 系统通信拓扑结构Fig.6 The topological structure of system communication

对于领导者和跟随者的系统参数矩阵给定如下:

假设该系统通信拓扑的切换过程满足半Markov过程,且有4 个不同的拓扑结构,如图6 所示,给定系统转移概率矩阵的变化域如下所示:

系统的其他参数设定为α=3,β=5,τ=0.8,σ=0.1,ξ1=0.4,ξ2=0.6,利用MATLAB 中的LMIs工具箱,求解矩阵不等式(33),可得系统的H∞参数为γ=0.6,控制器增益矩阵为

给定系统的初始状态为

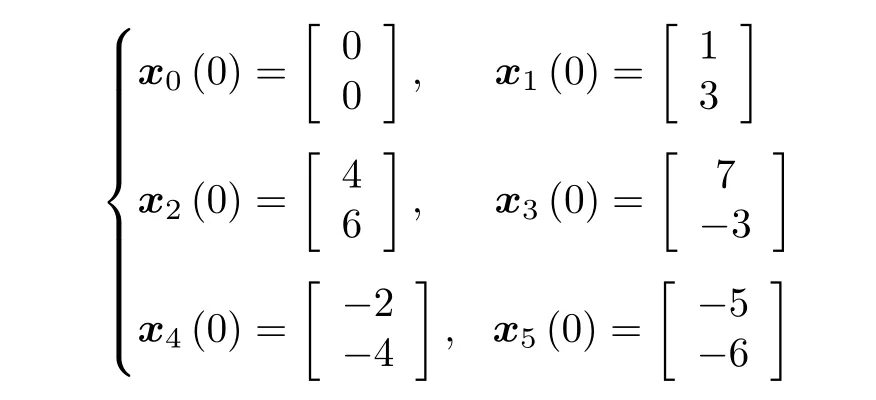
在控制器(4)的作用下,得到系统的状态响应曲线如图7和图8 所示,令系统的误差为e(t)=且误差曲线如图9 所示,系统通信拓扑的半Markov 切换信号如图10 所示.系统的状态响应图表明,5 个跟随者智能体的状态轨迹,在切换信号的影响下,能够逐渐向领导者智能体状态轨迹靠拢,在4.5 s 左右达到一致;误差曲线图9 表明,对于领导−跟随多智能体系统(1),在本文设计的一致性控制器的作用下,能够实现一致性控制,并具有较好的鲁棒性.另外,从图9 中响应曲线较大的数量级和较大的收敛斜率可以看出,在动态反馈控制作用下,图9 中响应曲线的峰值时间0.95 s,说明多智能体系统误差响应具有较快的收敛特性.

图7 状态变量xi1(t) 响应曲线Fig.7 The response of state variablexi1(t)

图8 状态变量xi2(t) 响应曲线Fig.8 The response of state variablexi2(t)

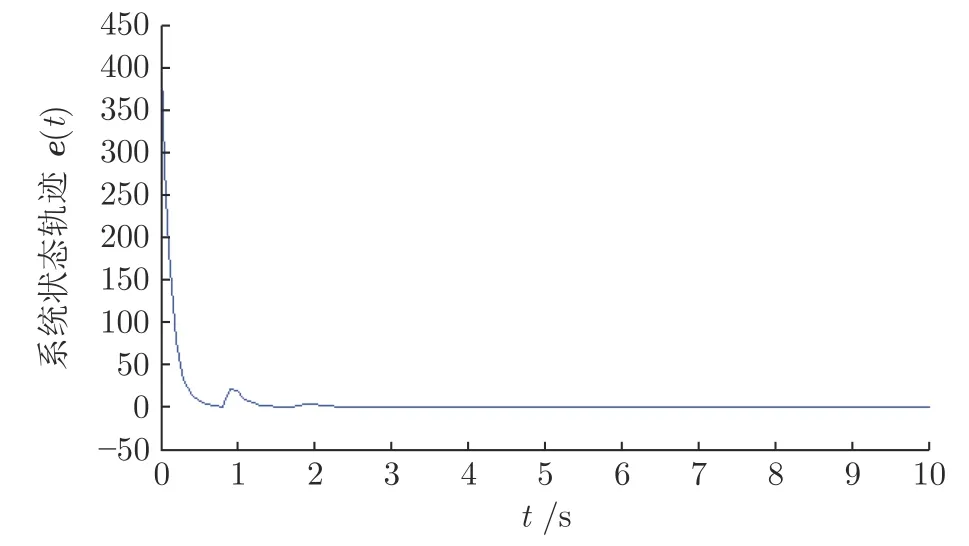
图9 系统误差e (t) 响应曲线Fig.9 The response of system errore(t)

图10 通信拓扑切换信号Fig.10 The switching signal of communication topology

本文给定的H∞性能指标用于描述设计的控制器对多智能体外界扰动ω(t) 的抑制效果,取值越小则抑制效果越明显.表1 给出了采用方法[37]和本文提出方法τM取不同值时γ下界对比结果.从表1可以看出,采用定理2 能够得到更小的γ下界.说明采用本文提出的控制策略提高了多智能体对外界扰动的抑制能力.

表1 τM 取不同值时γ 对比结果Table 1 Comparison results ofγ with differentτM

综合例1和例2,在均方一致性控制器(12)的作用下,随时间的增加,各个智能体与领导者的状态误差逐渐减小并趋于零.这表明采用本文提出的控制策略,该领导−跟随多智能体系统实现了领导−跟随一致性,协议有效性得到验证.

5 结束语

本文针对基于半Markov 跳变的带有通讯时滞和执行器故障的领导−跟随多智能体系统,设计一种新的动态反馈控制策略.根据领导−跟随多智能体系统的均方一致性和无领导者多智能体系统的渐近一致性要求,对系统进行线性变换,将多智能体系统的一致性问题转化为误差系统的稳定性问题.设计Lyapunov 函数,在一致性控制器的作用下,对于符合Lipschitz 条件的非线性项,通过求解线性矩阵不等式,实现误差系统稳定,并导出了误差系统H∞稳定的充分条件,从而保证了多智能体系统的一致性.最后,仿真结果表明基于线性变换设计的动态反馈控制器具有良好的控制性能,并且能够提高领导−跟随多智能体系统的动态特性.

无向拓扑结构显然是有向拓扑的一种特殊情况,即每个智能体均可以接收发送信息,这对智能体的传感器提出了很高要求,无形中增加了成本.相比于固定拓扑和无向拓扑图,有向拓扑图,突破了固定拓扑和无向拓扑的局限性,因此未来工作将在本文工作基础上研究有向切换拓扑条件下多智能体系统的H∞均方一致性控制问题,设计满足预定性能指标的分布式控制器.