基于深度强化学习的电力物资配送多目标路径优化

徐郁，朱韵攸，刘筱，邓雨婷，廖勇

（1.国网重庆市电力公司 永川供电分公司，重庆 402160；2.国网重庆市电力公司 信息通信分公司，重庆 401120；3.重庆锦禹云能源科技有限公司，重庆 400050；4.重庆大学 微电子与通信工程学院，重庆 400044）

0 引言

随着我国电力需求的不断增长、电网规模不断扩大，电力系统的物资需求量正在不断增加，保障电力物资的及时供应是亟待解决的问题［1］。强化学习（Reinforcement Learning，RL）对人工智能（Artificial Intelligence，AI）的发展产生了重大影响［2］，智能体（agent）在学习过程中定期作出决策，根据观察结果自动调整其策略以实现最佳决策。最近，由于深度强化学习（Deep Reinforcement Learning，DRL）的出现，克服了强化学习的局限性，从而为强化学习的发展开辟了一个新的时代［3］。DRL 利用深度神经网络（Deep Neural Network，DNN）的优势来训练学习过程，从而提高了学习效率和性能。在路径优化领域，DRL 已被用作有效解决各种问题和挑战的新兴工具［4］。

车辆路径问题（Vehicle Routing Problem，VRP）自提出以来，一直受到广泛关注与研究，此后VRP 被拓展到了更多的场景［5］。目前有多种智能算法可用于解决此类问题，例如扩展C-W（Extended Clarke and Wright，ECW）节约算法［6］、模拟退火（Simulated Annealing，SA）算法［7］、遗传算法［8］等。最近，应用DRL 来解决VRP 成为一种新兴趋势，例如文献［9］中提出了一种基于深度Q-网络（Deep Q-Network，DQN）的全局路径规划方法，机器人能在多障碍物中获得其最佳移动路径，仿真结果表明该方法相较于传统优化方法更高效，是DRL算法在路径规划领域成功的应用。针对装卸货问题（Pickup and Delivery Problem，PDP）的配对和优先级关系，文献［10］中设计了基于异构注意力机制集成的新型神经网络的DRL算法，为PDP 提供了更高质量的解决方案，但网络模型过于复杂，计算难度大。针对当前电力物资配送的信息化需求，文献［11］中建立了多中心、多场地和多配送需求的多点配送模型，但是该模型仅考虑了最短距离为目标。文献［12］中构建了电力应急物资配送路径优化的多目标优化模型，设计了改进的ε-constraint 算法进行求解，但是求解过程较为复杂。

对于电力物资配送路径优化问题，可以将其看作VRP的扩展，即电力物资车辆路径问题（Electric power material Vehicle Routing Problem，EVRP）［13］。针对现有EVRP 优化算法求解效率不高且模型考虑的目标较为单一、约束不全面的问题，本文在充分考虑了电力物资配送区域的加油站分布情况、物资运输车辆的油耗等约束，建立了以电力物资配送路径总长度最短、成本最低、物资需求点满意度最高为目标的多目标电力物资配送模型。为了提高模型求解效率，快速进行电力物资配送的路径优化，本文设计了一种基于DRL 的电力物资配送路径优化算法DRL-EVRP，将RL 与改进的指针网络（Pointer Network，Ptr-Net）结合成DQN，无需人为设计和调整繁杂的求解过程，DQN 使用一个记忆库来存储之前的样本数据，随机选择小批量样本进行网络训练，提高学习效率，可让DRL-EVRP 对电力物资配送的样本数据训练学习后，达到最优电力物资配送路径规划的效果，从而有效解决EVRP。实验结果表明，相较于SA 和ECW 算法，所提算法具有较优的求解结果，算法的运算时间在接受范围，从而可以快速准确地实现电力物资配送路径优化。

1 电力物资配送建模

1.1 问题描述

本文主要探讨电力物资配送路径优化问题，以电力物资配送总成本最小、满意度最高为优化目标，建立基于物资配送区域加油站网络、路径最短（运输时长最短）、考虑配送车辆载重量和配送车辆油耗的电力物资配送多目标路径优化模型。

电力物资配送路径优化问题可以描述为无向的完全图G=(V，E)，如图1 所示。其中顶点集由一个配送中心Vn（n=1，2，…，v）、物资需求点集I={I1，I2，…，Ii}和加油站集F={F1，F2，…，Ff}共同组成，即V={Vn}∪I∪F。于是可以用V={v0，v1，…，vm}来表示图G的顶点集，其中：顶点v0表示物资配送中心，m=1 +i+f；E={(vx，vy)：vx，vy∈V，x＜y}是连接V中各顶点边的集合，每个物资需求点有不同的需求量dx，每条边(vx，vy)都对应着路径长度disxy、运输时间txy和运输成本cxy。

本文电力物资配送路径优化问题的优化目标即为找到k条配送路径（每条路径对应一辆物资配送车辆），使得其电力物资配送总成本最小、物资需求点满意度最高。本文考虑路径最短、成本最低、物资需求点满意度最佳的配送多目标路径优化模型。每条配送路径从物资配送中心Vn出发，运输车辆前往每个物资需求点进行电力物资的货物卸载，当运输车辆油量不足时可前往加油站进行加油，最后回到物资配送中心，物资运输车辆的最大载重为Wmax，同时路径总运输时长不会超过驾驶员最大可接受驾驶时间Tmax，满意度由实际送达时间与期望送达时间的偏离程度来衡量。

为了更好地求解本文中电力物资配送路径优化问题，需要进行前提设置，具体如下：

1）物资需求点的需求量最大不超过运输车辆的载重；

2）一个物资需求点需要且只需要进行一次物资配送；

3）物资运输车辆行驶速度恒定，加油时间恒定；

4）每次加油后，运输车辆即为满油量状态，且加油次数不限；

5）满油量的运输车辆能从配送中心直接行驶到任一加油站，即不考虑离配送中心过远的加油站；

6）满油量的车辆从电力物资配送中心出发至任一物资需求点并返回配送中心过程中最多需要经过一个加油站，即不考虑过远的物资需求点。

1.2 电力物资配送模型

由于物资需求点必须且只能被访问一次，而加油站可能被访问多次，所以还需要将顶点集V扩大为V'=V∪Φ，其中Φ由虚拟点构成，即Φ={vi+f+1，vi+f+2，…，vi+f+f'}，每个虚拟点对应着一次对加油站的额外访问；相应地，E可扩充为E'，G'=(V'，E')。

根据上述分析与假设，本文建立的电力物资配送模型的目标函数为：

约束条件为：

其中：C1和C2分别为物资运输车辆固定成本和运输成本；a、b为物资需求点Ii对时间的敏感系数；Ti为物资期望送达时间；ti为物资实际送达时间，需求点在时间［Ti-ε，Ti+ε］内收到电力物资则满意程度为1，否则满意度会随偏离时间的加大而递减；ε为时间长度；Hi(ti)为ti物资送达时间下的物资需求点的满意度；I0表示物资配送中心和物资需求点集，即I0={v0}∪I；F0表示配送中心和加油站集，即F0={v0}∪F'，其中F'=F∪Φ；K表示所有运输车辆集合，即K={1，2，…，k}；txy表示运输车辆从点x到点y的时间；τy表示运输车辆到达点y后所花费的时间（从物资配送中心出发时，τ0=0）；px表示在顶点x所需要的时间服务时间（如果x∈I，则px为在物资需求点的服务时间，如果x∈F，则px为在加油站的加油所耗的时间）；qy为运输车辆到达y点后的剩余油量（到达物资配送中心和加油站加油后，令qy=Q）；r表示运输车辆的油耗速率；Q为运输车辆的油箱容积，也即运输车辆满油状态下的油量。

式（1）～（3）表示本文模型的优化目标；式（4）、（6）确保每个物资需求点有且仅有一辆运输车辆到达和离开；式（5）～（6）约束了至多有一辆运输车到达和离开加油站以及对应的虚拟点；式（7）～（8）表示至多有k辆车到达和离开物资配送中心；式（9）确保同一路径上的运输车辆到达时间遵从时间顺序；式（10）保证了每辆车的驾驶时间不会超过驾驶员的最长可接受的驾驶时间Tmax；式（11）确保运输车辆从物资配送中心出发后，到达任意一点都能在Tmax内回到物资配送中心；式（12）是运输车辆油耗情况；式（13）～（14）跟运输车辆油量相关；式（15）保证了运输车辆不会超重；式（16）约束了每个物资需求点只有一辆车服务；式（17）表示同一路径上的顶点由同一辆车进行电力物资运输；式（18）～（19）可分别表示为：

2 基于DQN的电力物资配送路径优化

Q-学习（Q-learning）算法是强化学习中经典的算法，它使用一个Q 值表（Q-table）来存储每个状态-动作对下的奖励值，通过智能体与环境的交互得到奖励值，然后更新Q 值表，使得选择奖励值最大的动作的概率不断增加，从而智能体能够获得最优的策略与奖励。假设智能体在时刻t下的状态为s，智能体根据策略选择动作a，智能体到达下一状态s'，环境反馈奖励值r，根据s、a和r更新Q 值表，更新表达式可表示为：

其中：α是学习率，γ是奖励的衰减率。不断对Q 值表进行更新直到达到最终状态。

在本文电力物资配送路径优化问题中，环境较复杂，状态数和动作数较多，Q 值表维度太高会导致Q-learning 算法效率很低，所以本文使用结合改进的指针网络（Ptr-Net）和Q-learning 的DQN 算法来解决此问题。

2.1 DQN结构

根据自然语言处理（Natural Language Processing，NLP）［14］，可以将本文中的EVRP 的解看作一个序列Y，则T+1可看作是序列的长度，序列模型的目标是最大化得到的序列的概率，即

其中：X={xi│i=0，1，…，M}表示输入，xi表示第i个节点的相关信息，M=i+f；Y={yt│t=0，1，…，T}表示最后输出的序列，yt表示第t个访问节点的序号；Xt表示在t时刻的输入；Yt={y0，y1，…，yt}表示截止到t时刻的输出；f(·)表示状态转移方程。将输入拆分成两部分，即xi={xi=(si，) │t=0，1，…，T}，si表示顶点i的坐标，与时刻t无关，始终不变；表示时刻t时物资运输车辆的剩余油量、路径的剩余时间、物资需求点的需求量以及满意度等，与时刻t有关，式（21）为输入信息的更新表达式，物资运输车辆离开了某个物资需求点时，该需求点的需求量更新为0。

传统的指针网络使用双向长短期记忆（Bi-directional Long Short-Term Memory，Bi-LSTM）网络作为编码器，使得网络增加了额外的复杂度，本文使用改进的指针网络来处理包含序列信息的数据，如图2 所示，省略了由Bi-LSTM 构成的编码器，并直接使用嵌入层的输入而不是Bi-LSTM 的隐藏状态，改进后在不降低模型的效率的同时可以降低计算复杂度。模型将输入Xt=(s，dt)通过一维卷积神经网络（One Dimensional Convolutional Neural Network，1DCNN）映射到高维空间，得到嵌入层（Embedding Layer）的输入，将输入到由LSTM 作为基本单元组成的解码器中，可得到解码器输出的隐藏状态值ht，将其与输入到注意力 层（Attention Layer），进而可得到输出。注意力机制计算表达式如下：

其中：式（24）～（25）计算得到的at为t时刻对各节点的注意力权重；式（26）为t时刻对各输入的线性加权的和，输出得到内容向量ct；式（27）计算下一时刻的概率分布；va、vc、Wa、Wc是可训练的参数。

DQN 算法使用改进的Ptr-Net 作为Q 值函数来代替Q 值表，本文所使用的神经网络结构如图2 所示，它的Q 值函数可近似表示为：

其中：s是当前智能体的状态；at是智能体在当前状态下选择的动作；θ为神经网络的参数。DQN 算法可以很好地解决状态空间大且是离散的问题［15］，从而保证数据处理的时效性，快速进行电力物资配送的路径优化，同时节约存储空间。

根据上述改进的指针网络，建立本文DQN 的结构如图3所示。DQN 中使用非线性方法表示Q 估计值函数，即Q(s，a；θ)，则DQN 中的损失函数定义为：

神经网络进行训练从而更新参数θ，参数更新表示为：

DQN 是一种离线学习方法，使用一个记忆库D 来解决连续样本间的相关性问题，D 中储存的是过去的电力物资配送路径优化经验，然后从D 中随机选择小批量样本进行网络训练，减小样本间的相关性，从而提高DQN 的学习效率［16］。使用新旧经验可以更加有效地训练神经网络，同时提高了经验数据的利用率。DQN 中神经网络部分由两个结构相同但参数不同的改进的指针网络组成，即估计网络和目标网络。估计网络作为主网络拥有最新的参数，输出当前状态-动作对下的Q 估计值Q(s，a)；目标网络不会及时更新参数，而是在训练时，每隔一定迭代步长c从估计网络将参数复制到目标网络中（网络克隆），它产生Q 目标值Q+(s，a)，用来评估当前状态—动作对下的损失函数，从而进行反向传播调整网络参数，具体过程见算法1。

本文基于DQN 的电力物资配送路径优化系统中的Q-learning 算法基本要素可表示为：

1）环境（environment）：电力物资配送网络。

2）智能体（agent）：电力物资配送路径优化系统。

3）动作（action）：在电力物资配送路径优化过程中，动作at可表示为在步骤t选择G'中一个顶点，其中∈V'。

4）状态（state）：状态st=(Lt)表示电力物资配送路径优化的部分解，其中Lt包含在步骤t之前所有经过的顶点，L0指物资配送中心。

5）奖励（reward）：为了最小化电力物资配送路径，本文首先假设成本与路径长度成正比关系，故而将奖励函数定义为路径长度的负值与满意度之和，因此奖励值可表示为R=，其中rt是在步骤t的累积增量路径长的负值-disxy与满意度累积和Hi，可以表示为：

6）策略（policy）：随机策略π从s0开始，在每个时间步下自动选择一个顶点，进入下一个状态st+1=，这个过程重复进行，直到完成所有的电力物资配送服务且满意度最高。执行该策略产生的最终结果是经过的顶点的排列，它规定了运输车辆访问每个顶点的顺序，即π={π0，π1，…，πT}，基于链式法则，输出解的概率［17］可表示为：

算法1 基于DQN 的电力物资配送路径优化。

输入 估计网络权值θ，目标网络权值θ̂=θ。

输出 已训练好的DQN 模型。

初始化：记忆库大小N；

2.2 网络训练与参数设置

基于DQN 的电力物资配送路径优化结构主要分为训练和路径规划两个部分，结构如图4 所示。

DQN 算法的核心在于训练神经网络［18］，为了使DQN 模型适用于电力物资配送路径优化场景，需要获取该场景下的足够多的电力物资配送系统的数据样本，利用这些数据样本对DQN 进行训练，通过迭代求解不断更新网络参数，得到最小均方误差下的最优参数。对于路径规划，此时DQN 已经学习完所有电力物资配送系统数据样本的特性，因此直接将训练好的DQN 进行电力物资配送的路径优化，得到最优电力物资配送路径。本文中网络训练相关参数设置如表1所示。

本文使用自适应矩估计（ADAptive Moment estimation，ADAM）算法［19］和随机梯度下降（Stochastic Gradient Descent，SGD）法更新神经网络的参数集，ADAM 算法与传统采用固定学习率的梯度下降算法不同，它可以在训练过程中自适应地更新学习率。使用批训练法进行训练，训练集大小设为20 000，验证集大小设为2 000；测试时采取随机抽样，样本大小设为500。

3 实验与结果分析

3.1 实验数据与仿真说明

为了验证本文所提的基于DQN 的电力物资配送路径优化算法的求解效果，下面使用Koç等［5］设计的10 个算例的数据和案例进行仿真实验，验证所提算法的实用性，每个算例的约束条件的设置值与文献［5］一致。每个算例可描述为在预先指定的时间限制内需要规划从一个仓库到一组分散的客户的货物运输成本最低的路线，并且不超过运输车辆的油箱容量的行驶里程，以最小化总路程或总成本，车辆的油箱容量有限，可以在需要时加油，车辆可以在加油站和仓库加油。

本次实验所使用的设备配置为图灵架构GeForce RTX 2080TI 显卡，Intel Xeon E5-2698 V4 处理器，RAM 64 GB；软件运行环境为Ubuntu 20.04 操作系统，Python 3.7，PyTorch 1.7 框架。实验中本文直接将训练好的DQN 用于电力物资配送路径规划中。

3.2 实验分析

本文DQN 在训练过程的损失变化曲线和奖励值变化曲线分别如图5～6 所示。图5中，可以看出随着迭代次数的增加，DQN 的损失值在不断下降，并且在训练迭代次数达到1 500 次时，DQN 已经基本可以达到想要的结果。图6中，包含累积迭代奖励值和累积平均奖励值，可以看出训练过程中前1 500 次迭代中奖励值在明显增加，这意味着电力物资配送的路径优化性能在不断提高，可以规划出路径最短、运输成本最低以及物资需求点满意度最高的配送路线的效果越来越好，经过2 000 次的迭代后，DQN 基本收敛，不管是迭代奖励值还是平均奖励值基本保持在-1 000 上下浮动。

接下来使用10 个EVRP 案例进行仿真实验，并对训练好的DRL-EVRP 与ECW［6］、SA 算法［7］求得的结果以及优化软件求得的最佳解UBest进行对比。对比结果如表2 所示，主要比较的是路径总长度f、各算法求得的结果与UBest的差距的百分比Gap以及满意度累积和Hi，其中物资需求点数和加油站数分别为20 和3、路径长度即为本文1.1 节中无向图顶点间的距离，即空间距离。

由表2 可知，对于大多数EVRP 案例来说，DRL-EVRP 求得的结果都比SA 和ECW 算法求得的结果更优；同时对于接近半数的EVRP 案例，DRL-EVRP 的求解结果要优于UBest的结果；就平均值来看，DRL-EVRP 的求解结果分别为f=1 626.00 km、Gap=0.54%和Hi=18.49，显然比SA 算法和ECW 算法要更优。

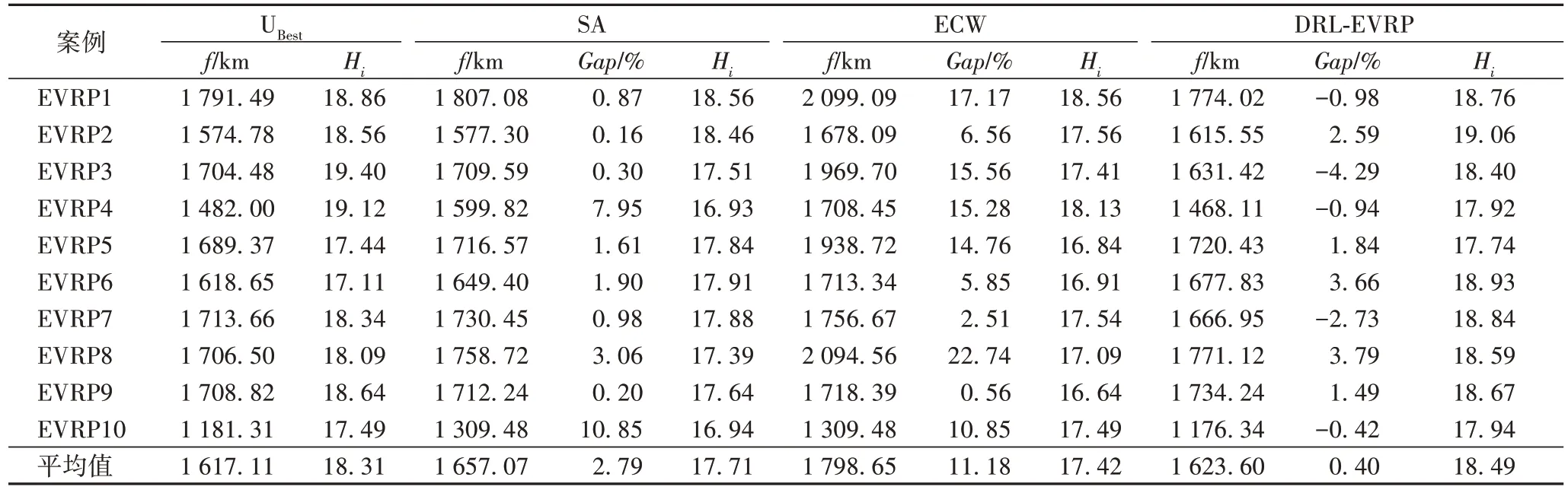
表2 各个算法对不同案例的求解结果对比Tab.2 Comparison of solution results of different algorithms for different cases

另外，在求解复杂度方面，文献［5］中指出，对于启发式的算法对每个案例求解时间均要小于1 s，但是对于优化软件求解出的UBest结果，在求解复杂模型时，是非常耗时的。不过，对于本文所提的已经训练好的DRL-EVRP 测试每个案例时，平均耗时在可接受的范围内，并且DQN 可以并行运行，因此可以减少算法运算时间［20］，从而快速进行电力物资配送路径优化。表3 给出了不同算法下求解不同案例所需的时间，可以看出本文算法平均运行时间为0.131 s，相较于SA 和ECW 算法总体在可接受范围内。

以案例EVRP1 为例，各点的经纬度坐标信息如表3 所示，其中第0 点为电力物资配送中心，第1～3 点为加油站，其余20 点为电力物资需求点。利用DRL-EVRP 对其进行求解，得到电力物资配送的5 条配送路径结果为：1）0-16-14-3-22-0，共432.27 km；2）0-6-9-11-19-21-2-0，共382.04 km；3）0-20-8-23-12-0，共292.43 km；4）0-15-13-10-1-18-0，共393.05 km；5）0-7-17-5-4-0，共274.23 km。合计得到5 条电力物资配送路径，其总长度为1 774.02 km。

表3 各个算法对不同案例的运行时间对比 单位：sTab.3 Comparison of running time of different algorithms for different cases unit：s

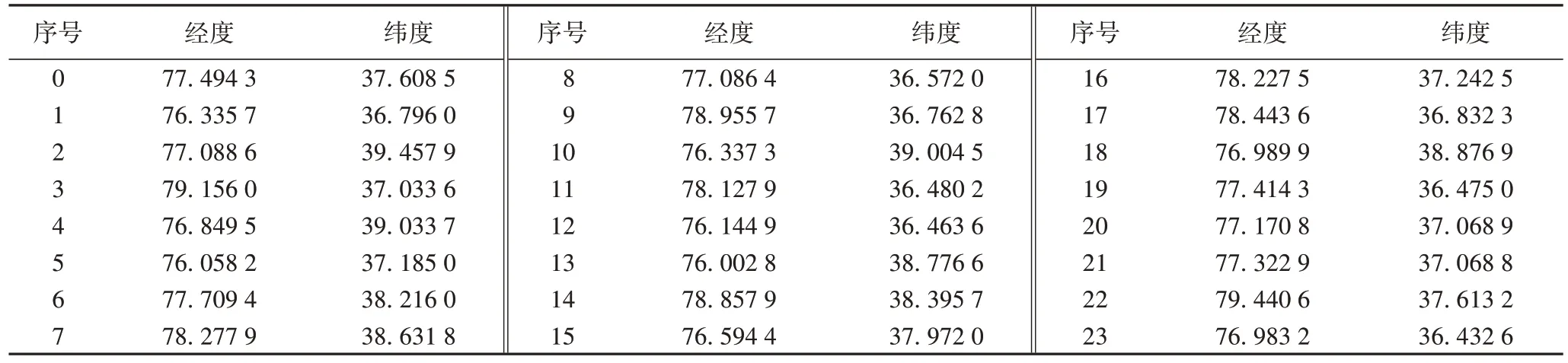
表4 案例EVRP1各点的位置信息Tab.4 Location information of each point in case EVRP1

4 结语

本文针对电力物资配送路径优化问题，提出了一种基于DRL 的电力物资配送多目标路径优化算法DRL-EVRP。首先，将EVRP 描述为无向的完全图，图的顶点集分别为物资配送中心、加油站和物资需求点。然后，在充分考虑了电力物资配送区域的加油站分布情况、运输车辆的载重量约束和车辆油耗等约束下，建立了特别针对EVRP 的以总运输路径长度最短、成本最低、物资需求点满意度最高为目标的电力物资配送模型。最后，基于强化学习设计了一种基于DRLEVRP 的路径优化求解算法，可快速规划出全局最优的电力物资配送路线，将电力物资输送至需求点。通过仿真实验验证了该算法在求解具有多约束条件下的EVRP 的有效性和收敛性，与ECW、SA 算法相比，该算法总体上具有更好的路径优化效果，能够规划出电力物资配送路径相对较短的路线，从而保证及时将电力物资配送至所有需求点。本文下一步的研究工作考虑将此算法扩展到更复杂的电力物资配送问题上，如具有电力物资配送优先级的EVRP。