基于抗退化混沌系统的动态S盒设计与分析

赵耿，张森民，马英杰，高世蕊

（北京电子科技学院 网络空间安全系，北京 100070）

0 引言

S 盒是分组密码的核心部件之一，也是众多分组密码唯一非线性部件，为分组密码提供了置乱作用，其性能与分组密码算法的安全性密切相关［1］，因此性能良好的S 盒对分组密码至关重要。S 盒主要有三种设计方法：随机构造法、数学构造法和将二者相结合的方法［2-4］。混沌系统具有伪随机性、遍历性和初值敏感性，与密码学扩散和混乱的安全要求有天然相似性，近年来被广泛应用于S 盒的设计中［5-6］。

文献［7］中提出了使用多个初始映射设计S盒，对S 盒做非线性操作，提高了S 盒的安全性能；但采用多重混沌映射会使系统运算效率降低。文献［8］中利用系统与Tent 映射拓扑共轭的性质，给出系统概率密度函数并进一步实现系统的均匀化；均匀化后构造的S 盒性能更优，但严格雪崩准则还有待提升。文献［9］中提出了一种采用三维Baker 混沌映射获取强S 盒的扩展方法，修正了二维Baker 混沌映射生成S 盒存在的缺陷，比二维Baker 映射具有更强的混沌特性；但混沌系统仍存在退化问题。文献［10］中研究开发了一个基于随机选择的S 盒生成器工具箱，可以使用经典随机函数和混沌系统类作为熵源，提升了S 盒的生成效率。文献［11］中提出了一种基于混沌验证码生成S 盒的方法，可用于验证门户网站和其他用户界面多媒体人机交互的安全性。文献［12］中提出了一种基于正弦映射构造S 盒的有效方法，能够产生高效非线性的随机整数序列；但不能动态批量地生成S 盒。

上述方法均在一定程度上使混沌系统生成S 盒的密码学性能更优、效率更高，但均未考虑所使用混沌系统在有限精度条件下会退化的问题［13］。混沌系统的退化是指，在有限精度条件下迭代一定次数后会落入周期轨道或固定在某一值，从而导致生成的混沌序列容易被预测，使S 盒存在安全隐患。同时，这一原因也是混沌密码走向实用的一大障碍［14-16］。

本文采用抗退化混沌系统生成S 盒：一方面能有效解决混沌系统生成序列退化问题，使之在数字有限精度下持续产生非周期序列，避免存在安全风险；另一方面可通过随机改变系统参数值批量动态地生成S盒，极大提升了S 盒生成效率。首先，设计了抗退化混沌系统部分，将量化的Lorenz 混沌系统扰动数字Chebyshev 混沌系统，使数字Chebyshev 系统生成的混沌序列周期大大延长。然后，设计了S 盒的生成，采用截取位数法和划分区间法生成两种初始S 盒S1、S2，再使用索引排序扰乱法生成最终S 盒。由于该方案可对抗退化混沌系统的参数在一定范围内随机调节，故可以动态批量地生成S盒［17］。

1 抗退化混沌系统设计

混沌系统在模拟状态下具有初值敏感性、遍历性和不可预测性等良好的动力学特性，但被运用到计算机等有限精度设备上时会发生退化行为。具体表现为迭代一定次数后混沌会落入周期轨道或固定在某一值，从而导致基于混沌的密码算法存在安全风险。为解决混沌退化问题，本文采用扰动法来抵抗数字混沌系统的退化：首先迭代模拟Lorenz 混沌映射1 000次，对1 000 次以后的数值进行离散采样；然后将采样后的值分别用于扰动Chebyshev 混沌映射的输入、输出和参数。系统结构如图1 所示，新构建的混沌系统迭代若干次后可生成无周期混沌序列，以此达到抗退化目的。

Lorenz 混沌系统的状态方程为：

Lorenz 系统原本是模拟的，但计算机无法处理模拟系统，所以需要将其进行离散化处理。采用Euler 算法进行离散采样，取采样时间为T=0.002，Lorenz 混沌映射采样后的表达式为：

当系统参数为σ=16，b=4，r=45.92 时处于混沌状态。

Chebyshev 混沌映射表达式为：

其中：β为系统参数，X(i)和X(i+1)为第i次迭代的输入和输出值。数值取值区间为［-1，1］。

利用Lorenz 混沌系统扰动Chebyshev 混沌系统的数学表达式为：

其中：x(i)、y(i)和z(i)分别为Lorenz 混沌映射采样后的3 个输出变量；Q(i)和W(i)分别为扰动输入和参数的中间变量。首先对数字Chebyshev 混沌映射的输入和参数进行扰动，如式（4）；然后，再对上一步的输出X(i+1)进行扰动，X'(i+1)为扰动输出后的结果，如式（5）。整体迭代式（4）～（5）即可生成抗退化数字混沌序列。

2 动态S盒构造算法

本文通过抗退化数字混沌系统动态生成8×8 的S盒，能有效避免传统数字混沌退化问题导致的安全风险，可使基于数字混沌系统生成的S 盒随机性更好、安全性更高。详细的S 盒生成方法如下所述：

步骤1 先对Chebyshev 混沌映射赋初值X(0)=0.25，系统参数β=8；再迭代Lorenz 混沌映射，对Lorenz 混沌映射设初值x(0)=1，y(0)=1，z(0)=1，系统参数设为σ=16，b=4，r=45.92，舍去前1 000 次迭代的数值后生成三组离散混沌序列｛x｝、｛y｝、｛z｝，分别用于扰动数字Chebyshev 混沌映射的输入、输出和参数；然后再将式（4）～（5）迭代5 000次，即可生成第一个混沌序列。

步骤2 步骤1 迭代完5 000 次后，改变系统参数可生成不同的混沌序列，对Lorenz 混沌系统的参数数值σ累加0.04，继续迭代5 000 次则生成新的混沌序列，以此类推可生成500 个混沌序列{X1}，{X2}，…，{X500}，每个序列数值个数为5 000。

步骤3 采用截取位数法生成初始S 盒S1。准备长为256的空 S 盒 S1，对第一个混沌序列X1={X1(0)，X1(1)，…，X1(5 000)}的第一个值X1(0)截取小数点后的前4位，对X1(1)截取第5 至8位，对X1(2)截取第9～12位，依此类推，截取第13～16 位后返回截取前4 位。然后将截取的值分别模256，按顺序将所得数值存入S1 盒中，如果待存入值在S1 盒中已存在，则舍去该值继续存下一个直至S1盒存满。

步骤4 采用划分区间法生成初始S 盒S2，准备一个长为256 的空S 盒S2，将［-1，1］等分为1 000 个小区间，并为每个小区间标上序号i(i=1，2，…，1 000)。判断第一个混沌序列X1={X1(0)，X1(1)，…，X1(5 000)}中每一个值所在的区间，并将每一个区间号模256，然后将所得数值按顺序存入S2 盒中，如果待存入值在S2 盒中已有，则舍去该值继续存下一个直至S2 盒存满。

步骤5 采用索引排序扰乱法生成最终S 盒S3，准备长为256 的空S 盒S3，令S2 盒的256 个值作为S3 盒的索引序号，按顺序把S1 盒中的256 个值分别放入S3 盒中对应索引序号的位置，从而完成初始S 盒的扰乱，可有效增强其随机性。

步骤6 对步骤2 生成的其余混沌序列重复步骤3～5，即可动态生成500 个8×8 的S 盒。图2 为生成的一个S 盒的示例。

3 抗退化混沌系统性能分析

本文对改进后系统的轨迹图、初值敏感图和吸引子图进行分析，以验证是否具有遍历性、初值敏感性和不可预测性。原始数字Chebyshev 混沌系统在迭代一定次数后会成为周期序列，如图3；改进后系统生成的序列周期被极大延长，迭代500 次以上仍保持无规则的轨迹，说明生成的数值不可预测，系统是无退化的，如图4。

在低有限精度情况下，如果系统的输入初值有很小改变，迭代一定次数后运动轨迹会完全不一样，则说明系统具有初值敏感性。在保持两个系统其余参数不变的情况下分别使初始值为0.250 000 00 和0.250 000 03，图5 是两个系统的轨迹图。可以看出，即使输入差别很小迭代若干次后二者轨迹截然不同，说明系统具备初值敏感性。

数字混沌系统的吸引子呈点状分布。数字混沌系统的吸引子分布得越随机、越均匀，说明混杂效果越好。数字Chebyshev 混沌系统的吸引子只分布在几个固定的点上，改进系统的吸引子均匀分布，如图6 所示，说明系统混杂效果好，具有遍历性。

4 S盒安全性能分析

4.1 非线性度

令f：→F2为n元布尔函数，则f(x)的非线性度为：

其中：dH(f，l)为f与l的汉明距离；Ln为仿射函数集。

本文通过Walsh 谱计算函数的非线性度，表达式为：

其中：x·ω为x与ω的点积，即x·ω=x1ω1⊕x2ω2⊕…⊕xnωn。在S 盒安全分析中，非线性度越高说明抵抗线性分析的能力越强。表1 是本文S 盒非线性度值与其他方案的比较，每一种方案共有8 个非线性度值，求出各自均值后比较可以看出本文S 盒的非线性度平均值达到106.00，高于文献［9，14-15］的平均值，因此其抵抗线性分析的能力更强。

表1 不同方案的非线性度对比Tab.1 Nonlinearity comparison among different schemes

4.2 差分均匀性

差分均匀性是衡量S 盒抵抗差分分析能力的重要指标，文献［14］给出了差分均匀性的计算方法，对于多输出函数S(x)=(f1(x)，f2(x)，…，fm(x))：，差分均匀性计算公式如下：

其中：∂∈GF(2n)，β∈GF(2n)，#表示计数。

差分逼近概率［2］也可用来衡量差分分布的性能：

其中：DP表示输入差分确定情况下，输出差分Δy的最大可能性；X表示全部可能输入情况的集合；2n为集合中的元素个数。

最大差分值越小表明S 盒的差分均匀性越好，抗差分攻击能力越强。表2 展示了与其他文献方案的对比结果，文献［10］最大差分值为10，文献［10-13］最大差分值为12，本文方案的S 盒最大差分值为10，具有更好的抗差分攻击能力。

表2 不同方案的最大差分值对比Tab.2 Maximum difference comparison among different schemes

4.3 严格雪崩准则

严格雪崩准则（Strict Avalanche Criterion，SAC）是指当输入变量改变1 比特时，会导致输出有一半的比特发生改变。通常构造相关矩阵来验证布尔函数是否满足严格雪崩准则，若每个元素的值越接近0.5，则说明越满足严格雪崩准则。本文S 盒的SAC 相关矩阵如图7 所示。最大值和最小值分别为0.593 8、0.406 3，平均值为0.499 3，与0.500 0 只相差0.000 7。与其他文献的对比结果如表3 所示，本文SAC 值比文献［10-13］的S 盒更接近理论值0.500 0，表明该系统满足严格雪崩准则，具有相对更好的安全性能。

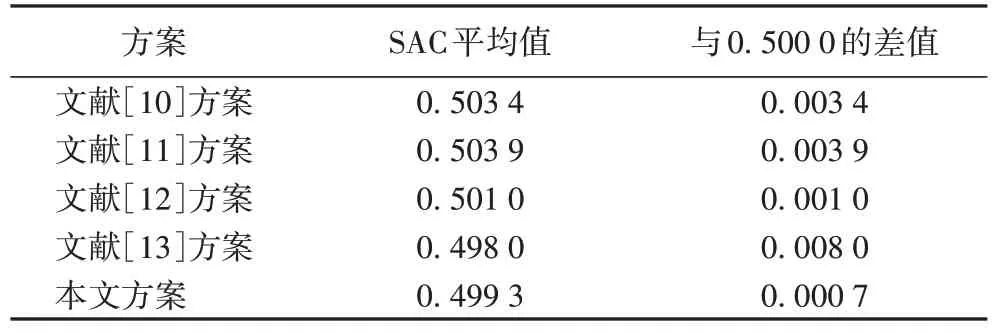
表3 不同方案的严格雪崩准则对比Tab.3 Strict avalanche criterion comparison among different schemes

4.4 输出比特间独立性

范明慧等［14］提出了验证系统是否满足输出比特间独立性（Output Bits Independence Criterion，BIC）的方法，可通过计算S 盒的任意两个输出比特fj和fk异或的值fj⊕fk是否满足严格雪崩准则来确定，运算结果越逼近于理论值0.500 0，说明一个输入比特取反的情况下，越能保证输出比特对相关系数越接近于0。本文构造S 盒的相关矩阵数值如图8 所示，平均值为0.499 9，与理论值0.500 0 仅相差0.000 1；与其他文献方案的对比如表4 所示，文献［10］方案的平均值为0.497 2，文献［11］方案的平均值为0.507 8，文献［12］方案的平均值为0.498 8，文献［13］方案的平均值为0.501 3，对比发现本文方案的输出比特间独立性更强。

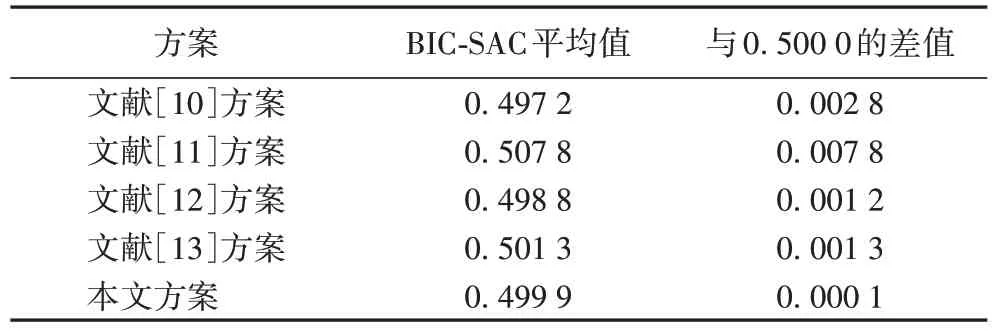
表4 不同方案的输出比特间独立性对比Tab.4 Comparison of output bits independence criterion among different schemes

4.5 双射特性

在实际的加密运用中，S 盒通常要求可逆，在代换-置换网络（Substitution Permutation Network，SPN）型分组密码结构中，S 盒必须满足此条件。S 盒满足双射的充分必要条件为各分量条件的布尔函数之和为2n-1，即

其中 ：fi为 S 盒的第i个分量的布尔函数ai∈{0，1}(a1，a2，…，an) ≠(0，0，…，0)；ωt(·)表示汉明重量。若式（10）成立，说明每个fi满足0/1 平衡，且满足双射条件。

由式（10）可知，当n=8，满足双射性的标准值是128，通过计算，本文S 盒所有分量的布尔函数之和均为28-1=128，因此该S 盒是双射的。

5 结语

本文首先提出抗退化混沌系统的构造方案，使用Lorenz混沌系统扰动数字Chebyshev 混沌系统，使生成混沌序列的周期大幅延长；然后，在此基础上，采用截取位数法和划分区间法生成两种8×8 的初始S 盒；最后，通过索引排序扰乱法生成最终S 盒。由于Lorenz 混沌系统的参数可在一定范围内随机切换，故可批量生成S 盒。最终对抗退化混沌系统和生成的S 盒进行分析与对比，实验结果表明，该混沌系统具有遍历性、初值敏感性和不可预测性，并且数据具有比模拟状态下更好的随机性。S 盒的非线性度、差分均匀性、严格雪崩准则、比特间独立性等性能优于近年来文献的方案，具备较为优秀的密码学性能。而且相较于其他数字混沌方法生成的S盒，采用的混沌序列不仅不存在短周期行为、随机性更好，能消除生成源上的安全隐患，而且还能批量动态地生成S盒，所以该方案生成的S 盒运用于分组密码具备更优的安全性能。下一步计划将本文S 盒用于分组密码算法设计和图像加密相关领域的研究。