基于高阶自包含协同过滤的有向网络链路预测

陈广福，王海波，连雁平

（1.武夷学院 数学与计算机学院，福建 武夷山 354300；2.认知计算与智能信息处理福建省高校重点实验室（武夷学院），福建 武夷山 354300；3.湖南科技学院 信息工程学院，湖南 永州 425199）

0 引言

真实世界大量的复杂系统可使用复杂网络来描述和表示。在复杂网络中节点代表实体而链接表示实体间关系。然而，由于构建真实复杂网络时受复杂系统复杂性、噪声及实验条件等影响，所构建复杂网络容易出现缺失链接及冗余链接。因此，如何寻找缺失链接是复杂网络研究最有挑战的问题。链路预测目标是根据已知网络结构及其节点属性等去推断节点对形成链接的可能性［1］。此外，链路预测还具有以下两个功能：1）它可以预测缺失链接包括无向、加权和方向链接以及识别虚假链接；2）根据当前网络结构信息去演绎网络演化过程。因此，链路预测广泛应用于不同领域。例如在电子邮件系统，链路预测可阻止和过滤不相关及广告邮件［2］；在社交网络，链路预测启用信任度量保护用户隐私信息［3］；在生物网络中，可用于预测蛋白质间先前未知相互作用，从而显著降低经验方法的成本等［4］。

现存大部分链接预测方法把有向网络看作无向无权网络而忽略链接方向，导致预测不准确。然而，大部分真实世界网络是有向网络，例如交通运输网络、食物网、生物网和在线社交网等。不同类型有向网络中，链接方向表示不同含义。例如在食物网中，链接方向表示不同种群捕食关系；在线社交网络中，链接方向代表不同用户不对称的关系；在交通运输网中，链接方向表示站点间运输频率。因此，忽略链接方向信息会导致预测结果与实际结果存在着重大偏差［5］。现存大部分链路预测仅关注无向无权网络，有向网络的链接预测问题处于起步阶段，因此如何挖掘和利用链接方向及有向网络结构信息是个挑战问题。近10 年来，一些研究人员关注有向网络链路预测并取得一定进展。例如Schall等［6］提出基于闭合三元组比率的链路预测方法，结果表明该方法提高了有向网络预测精度；Bütün等［7］扩展文献［6］中的闭合三元组，提出基于模式有监督的闭合三元组方法；Zhang等［8］将无向无权局部相似度方法扩展到有向网络，构建有向局部相似度方法，结果表明这些方法可有效预测缺失有向链接和鉴定虚假链接；Bütün等［9］在文献［8］的基础上进一步考虑权重和时序信息，改善算法性能。尽管以上方法预测准确度有明显提高，但是这些方法仅直接利用链接方向或网络局部结构，无法适用于稀疏网络。此外，Shang等［10］提出有向网络节点的相位动态算法来分析链接方向的作用，并证明双向链接和单向链接在链路预测和网络结构形成方面具有不同的作用；Zhang等［11］提出基于势能理论不同模体预测指标，结果表明Bifan 预测准确度最优；Li等［12］在文献［10-11］的基础上利用零模型验证互惠连接作用并考虑权重信息提出间接互惠感知加权（Indirect Reciprocity-aware Weighting，IRW）框架和直接互惠感知加权（Direct Reciprocity-aware Weighting，DRW）。以上研究仅讨论互惠连接作用，然而当有向网络可观察链接较少时，无法捕获更多网络结构信息降低预测精度。此外，Pech等［13］提出线性最优化（Linear Optimization，LO）方法，该方法将节点邻居的邻居用线性和表示获取网络高阶路径信息；李劲松等［14］在文献［13］的基础上提出线性规划方法，与LO 有相似作用。尽管以上方法在一定程度提高了有向网络预测准确性，然而它们共同缺点是无法获取有向网络更多结构信息而敏感于稀疏网络。针对以上问题，Chen等［15］提出联合有向网络局部和全局结构的非负矩阵分解链路预测方法弥补网络稀疏性，然而该方法附加额外信息增加算法复杂度。

协同过滤方法是推荐系统中经典算法，Lee等［16］提出基于协同过滤和自包含协同过滤理论框架，再融合局部相似度方法构建一系列新链路预测方法。然而，该方法有两个不足：首先，以上两个框架仅考虑无向无权网络而无法处理有向网络问题；其次，该方法仅考虑一阶相似度而无法捕获更多网络结构信息去处理网络稀疏性和冷启动问题。链路预测中冷启动是指孤立节点及新节点缺乏足够的网络拓扑结构信息而难以与其他节点形成链接。本文受文献［16］的启发，将解决以下两个问题：1）将协同过滤方法扩展到有向网络；2）获得更多有向结构信息去处理网络稀疏性和冷启动问题。具体地，首先采用随机游走算法计算任意节点间的k步转移概率矩阵去捕获有向网络全局结构信息。此外，随机游走算法的优点是可捕获有向网络每个节点的信息及邻居信息，从而有足够网络结构信息弥补稀疏性和冷启动不足；再利用全局结构信息来替代自包含协同过滤框架中的一阶相似度，构建高阶自包含协同过滤（High-order Self-included Collaborative Filtering，HSCF）理论框架；再分别将三个有向局部相似度指标，即有向共同邻居（Directed Common Neighbor，DCN）、有 向Adamic-Adar（Directed Adamic-Adar，DAA）和有向资源分配（Directed Resource Allocation，DRA）和一个三阶Bifan 指标，与HSCF 框架相融合构建4 个有向网络链路预测方法，分别为：HSCF-DCN、HSCF-DAA、HSCF-DRA和HSCF-Bifan。为验证所提预测指标性能，在10 个真实世界有向网络上与基准指标进行比较，结果表明所提指标预测精度获得显著提升。

1 本文方法

1.1 问题描述

给定一个有向无权网络G(V，E)，其中V=是节点集和E表示链接集，每条边e∈E表示一个有序对e=(νi，νj)，其中|V|是节点数，|E|是链接数。本文不允许多个链接和自循环存在。本文用X=[xij]N×N来表示G的邻接矩阵，显然xij≠xji。若G是有向无权网络，如果节点νi→νj之间存在链接，则xij=1；否则xij=0。设表示任意节点i入度，则表示任意节点i出度以及Γout(i)和Γin(i)分别表示节点i的共同邻居出度和入度。此外，本文用U=|V|(|V| -1) 2 表示任意有向网络所有节点间的链接，显然不存在链接集则为U-E。链路预测的目标是从不存在集合U-E中查找缺失链接。为了验证算法性能，将观测到的链路集E随机分成训练集ET和测试集EP两部分，前者是已知信息而后者仅用于测试，显然，ET∩EP=∅和ET∪EP=E。

1.2 高阶转移概率矩阵

大部分真实有向网络具有稀疏性，仅考虑局部结构是远远不够的。本文启用随机游走算法［17］计算k步转移概率矩阵来保持全局结构。随机游走方法［17］核心思想是从有向网络任意节点出发经过k步后到达另外一个节点概率。例如当k=3 时可以计算出任意节点间三阶路径去保持节点邻域信息。设任意有向网络邻接矩阵X，转移矩阵为表示任意节点i随机游走k到达节点j，k步转移矩阵定义如下：

为减小算法时间复杂度，本文分别令k=3和k=4 可得到三阶和四阶转移矩阵，分别如下：

为方便理解式（2），设任意8 个节点和13 条有向链接，采用随机游走方法获得三阶转移矩阵的过程。从图1 可观察到原始有向网络中节点1 和8、节点1 和7、节点1 和6 不存在有向链接。启用随机游走方法计算三阶转移矩阵再还原初始有向网络时，节点1 和8、节点1 和7、节点1 和6 均产生有向链接，具体原因是节点1→2→8、节点1→3→7 和节点1→3→6 存在着三阶链接，因此，通过随机游走算法均产生有向链接。而节点1 和5 没有产生链接的原因是节点1 和5 间不存在三阶连接关系。最后，通过三阶转移矩阵还原初始网络可观察到节点间存在着三阶有向链接均产生链接，表明通过该方法可捕获更多网络拓扑结构信息，提高预测有向链接准确度。

1.3 高阶自包含协同过滤预测框架

设任意无向无权网络邻接矩阵A∈Rn×n，自包含协同过滤（Self-included Collaborative Filtering，SCF）［16］理论框架定义如下：

其中：I是单位矩阵。

式（4）有以下两个不足：1）该式仅适用于无向无权网络，无法处理有向网络链路预测问题；2）该式直接启用邻接矩阵而无法捕获更多网络结构信息。因此，本文将式（4）扩展到有向网络，只需将式（2）～（3）替换式（4）中初始邻接矩阵A，重写式（4），有

其中：M3和M4分别是三阶和四阶相似度。

1.4 所提指标

在式（5）的基础上融合4 个经典有向网络链路预测指标（DCN、DAA、DRA 和Bifan）分别构成4 个不同半局部有向网络链路预测指标，以上指标同时可保持有向网络局部和全局网络结构信息。接下来介绍4 个经典有向网络链路预测指标：

1）有向共同邻居（DCN）指标。将共同邻居方法扩展到有向网络中，节点间共同邻居越多相似的可能性就越高，定义如下：

2）有向Adamic-Adar（DAA）指 标。扩 展AA（Adamic-Adar）指标到有向网，其核心是抑制共同邻居中较大度的节点，定义如下：

3）有向资源分配（DRA）指标。该指标扩展RA（Resource Allocation）到有向网，从资源分配角度出发，其核心思想是共同邻居传送资源数量与其出度成反比关系，定义如下：

4）势能理论（Bifan）指标。该指标是基于势能理论，聚类特性及同质性假设，筛选出最优模体Bifan，考虑节点三阶路径，定义如下：

将以上4 个指标融入式（5）中，并用可调参数α∈[0.1，0.9]控制所提所有指标三阶和四阶相似度在链路预测中所起的作用。所提4 个基于HSCF 链路预测指标定义如下：

本文所提的4 个指标具有平衡有向局部和全局结构信息的作用，有利于探索更多网络结构信息提高预测精度。α用于平衡三阶路径和四阶路径所占比例：若α＞0.5 表明四阶路径信息比例高于三阶路径信息；若α＜0.5 表明三阶路径信息比例低于四阶路径信息。

本文所提HSCF-DCN、HSCF-DAA、HSCF-DRA 和HSCFBifan 指标计算AUC和F-score的伪码如下所示。

输入 任意有向网络G(V，E)，可调参数α。

输出AUC和F-score。

步骤1 将任意有向网络转化为邻接矩阵；

步骤2 按9∶1 的比例将原始网络划分为训练集和测试集；

步骤3在G中遍历所有节点；

步骤4 根据式（4）计算高阶相似度矩阵；

步骤5 式（2）～（3）和式（5）融合构建高阶自包含协同过滤框架；

步骤6 将式（6）～（9）替换式（5）中任意相似度S；

步骤7 式（10）～（13）是本文4 个指标预测概率矩阵；

步骤8 计算平均AUC和F-score。

1.5 算法时间复杂度

所提4 个指标耗时主要是集中使用随机游走方法计算三阶和四阶转移矩阵。如算法1 所示，所提指标在步骤3～5耗时为O(Nl)，l是步长。此外，在步骤7中，DCN、DAA、DRA和Bifan 耗时均为。因此，本文所提指标的时间复杂度为大规模网络和稀疏网络中l是有限长度及≪N，因此时间复杂度为O(n)。

2 实验与结果分析

2.1 评价度量

本文使用受试者工作特征（Receiver Operating Characteristic，ROC）曲线下方面积AUC（Area Under Curve of ROC）［18］和F分数（F-score）［19］两个度量去衡量所有指标性能。具体定义如下：

1）AUC可以理解为在测试集EP中的链接分数大于随机选择一个不存在集U-E中链接分数概率。独立比较n次，若有n1次测试集中链接的分数值大于不存在集中的链接分数，有n2次两分数值相等，定义如下：

2）F-score度量是召回率（Recall）和精确率（Precision）综合性度量，可更全面和有效评价算法性能，定义如下：

2.2 数据集

本文采用10 个真实世界有向网络评价所有方法的性能，其拓扑结构特征统计在表1 中。其中，N=|V|是节点数，M=|E|是链接数，和分别表示节点最大入度和出度，平均度是网络总边数与节点数的比值，稀疏率表示有向网络稀疏程度。10 个有向网络的数据集介绍如下：

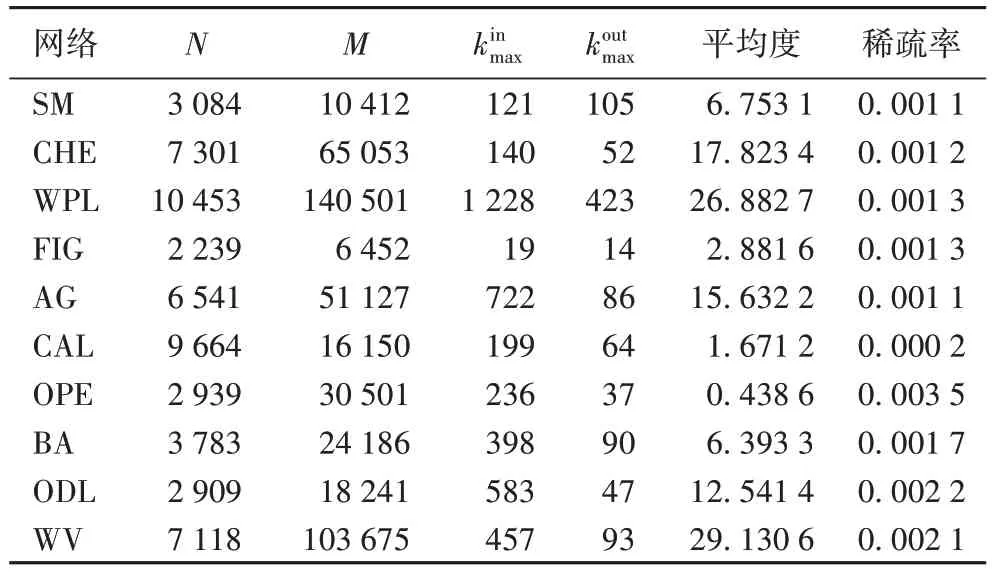
表1 10个真实世界有向网络的拓扑结构特征统计Tab.1 Topological feature statistics of 10 real directed networks

1）国际象棋网络CHE（CHEss）［20］。该网络是国际象棋比赛的结果，由7 301 节点和65 053 条链接构成，节点表示一个棋手，有向边表示一个游戏。

2）维基百科网络WPL（Wiki Pedia Links）［20］。该网络收集于低地撒克逊语维基百科，由10 453 节点和140 501 条链接构成，节点表示维基百科文章，有向边代表维基链接，即一个维基中的超链接。

3）搜索引擎网络CAL（CALifornia）。该网络通过hub/authority 算法去搜索引擎查询“California”而构建，由9 664 节点和16 150 条链接构成。

4）信任网络AG（AdvoGato）［21］。AG 是一个为自由软件开发者提供在线社区平台的信任网络，由6 541 节点和51 127 条链接构成，节点表示用户，有向边表示节点间的信任关系。

5）论文引用网络SM（SciMet）［22］。该网络是关于网络理论与实验引用网络，它由3 084 个节点和10 412 条链接组成。

6）航空网络OPE（OPEnflights）［20］。该网络是世界各机场之间的航班数据集，节点表示机场，有向链接表示从一个机场到另一个机场航班。

7）蛋白质交互网络FIG（FIGeys）［20］。该网络是人类蛋白质之间相互作用的网络，节点表示蛋白质，方向链接表示蛋白质间交互关系。

8）图书馆与信息科学在线词典ODL（ODLis）［22］。它是各类图书馆和信息专业超文本参考资源。

9）信任网络BA（Bitcoin Alpha）［22］。它是在Bitcoin Alpha平台上人与人信任关系，节点表示匿名用户，方向链接表示匿名用户间信任关系。

10）英语维基百科WV（Wiki Vote）［20］。该网络收集于英语维基百科用户网络，在管理员选举中相互投了赞成票和反对票，节点表示单个用户，有向边表示投票。

2.3 基准指标

为验证所提指标性能，本文启用12 个基准指标与之比较。12 个基准指标介绍如下：

1）基于有向局部相似度（DCN、DAA 和DRA）［8］和基于势能理论Bifan，已在1.4 节作了详细说明。

2）线性最优化（LO）［13］。该指标假设两个节点之间存在链接可能性可以通过相邻节点线性求和来展开。

其中：α是可调参数。

3）大度节点有利指标（Hub Promoted Index，HPI）［23］。该指标表示代谢网络中两节点端点的相似程度。

4）Jaccard 指标［23］。该指标表示是两个顶点共同邻居数比上两节点所有邻居数之和，其定义如下：

5）局部路径（Local Path，LP）指标［23］。该指标扩展共同邻居指标，该指标考虑三阶路径因素捕获高阶和二阶路径。

其中：α是可调参数。

6）间接互惠感知加权（Indirect Reciprocity-aware Weighting，IRW）指标与经典有向网络指标（DCN、DAA、DRA和Bifan）构建的新指标，分别为IRW-DCN、IRW-DAA、IRWDRA 和IRW-Bifan。

2.4 实验结果分析

本文实验硬件平台为Intel Core i5-6500 CPU 台式电脑，主频3.20 GHz、内存8 GB 和操作系统Windows 10，所有方法使用Matlab R2016b 实现。

本文通过4 个实验评估所提指标性能：1）启用AUC 和F-score度量全面评估基准指标和本文所提指标性能；2）基准指标和本文所提指标鲁棒性对比；3）对可调参数敏感性分析；4）所提指标在10 个真实有向网络上运行时间对比。

对于实验一，将原始有向网络按9∶1 的比例随机划分为训练集和测试集，再使用AUC和F-score度量评估所有指标性能，其实验结果记录在表2～3中，并观察到以下几个现象：

1）所提指标在所有有向网络上表现出良好预测准确度。由表2 可知，在绝大部分有向网络上，本文4 个指标均获得最优性能，且相较于基准指标，HSCF-DCN、HSCF-DAA、HSCFDRA 和HSCF-Bifan的AUC分别平均提高了8.16%、8.85%、9.64%和10.33%；由表3 可知，所提指标在所有数据集上均获得高质量性能，且相较于基准指标，HSCF-DCN、HSCFDAA、HSCF-DRA 和HSCF-Bifan的F-score分别平均提高了66.62%、68.32%、68.95%和76.18%。以上表明捕获更高阶路径信息有助于改善有向网络预测精度。

2）表2中，与经典有向局部相似度（DCN、DAA、DRA、Jaccard 和HPI）相比，所提指标的预测精确有显著提高。例如在数据集SM、OPE、CHE 和WPL中，所提最优指标HSCFDRA 与基准最优指标DRA 相比，AUC分别提升了10.71%、2.47%、21.80%和6.77%。经典方法获得低质量性能主要原因是它们考虑有向网络局部结构信息而敏感于稀疏性。此外，与半局部指标LP 和Bifan 相比，所提指标依然胜过LP和Bifan。例如在数据集BA 和ODL中，所提最优指标HSCFDRA 与基准最优指标Bifan 相比，AUC分别提高了4.83%和1.37%。它们获得低预测精度是由于LP 和Bifan 仅考虑节点三阶路径或节点邻居的节点信息。与全局指标LO 相比，所提指标全面胜出，尤其在数据集CHE、BA、ODL 和CAL 中表现特别突出。例如在CAL，所提最优指标HSCF-Bifan 与LO相比，AUC提升了13.96%。表明全局指标在稀疏网络采集不到更多有用结构信息，而所提指标采用局部加全局更有利于捕获更多网络结构信息。所提指标与基于互惠感知加权机制指标相比，所提指标依然优于它们，然而在WV 数据集，Bifan 性能最佳，表明该指标可有效利用三阶路径信息。

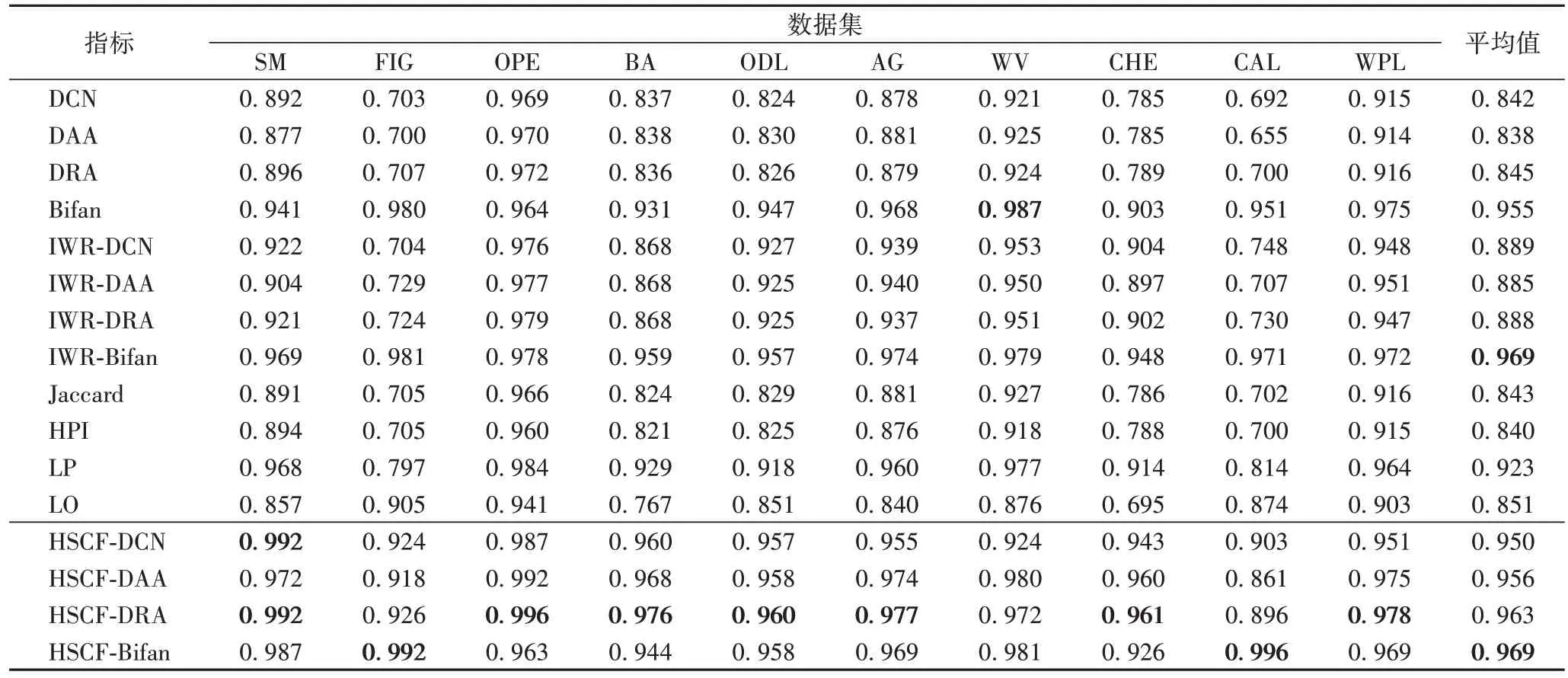
表2 不同指标下的AUC对比Tab.2 Comparison of AUC under difference indices

3）F-score是召回率和精确率加权平均调和，因此该度量更能全面评价算法性能。由于数据不平衡导致召回率和精确率相互矛盾，启用F-score可更客观评估所有指标性能。由表3 可观察到所提指标在10 个数据集中都获得高质量性能。与经典有向局部相似度（DCN、DAA、DRA、Jaccard 和HPI）相比，所提指标有显著提升。例如在数据集SM 和FIG，所提最优指标HSCF-Bifan 与基准最优指标HPI 相比，F-score分别提升了14.12%和89.65%。基于互惠感知加权机制方法比较接近本文指标性能，主要原因是前者方法采用权重机制捕获更多互惠链接信息，尤其IRW-Bifan 最接近本文4 个指标的主要原因是该指标利用权重机制捕获更多互惠链接及融合三阶路径信息，例如在数据集BA 和ODL；而半全局指标LP和Bifan 获得较低综合性能主要原因是仅考虑三阶路径信息；全局指标LO 比较接近本文所提指标性能，是由于LO 采集网络所有节点路径，有稳定预测精度。

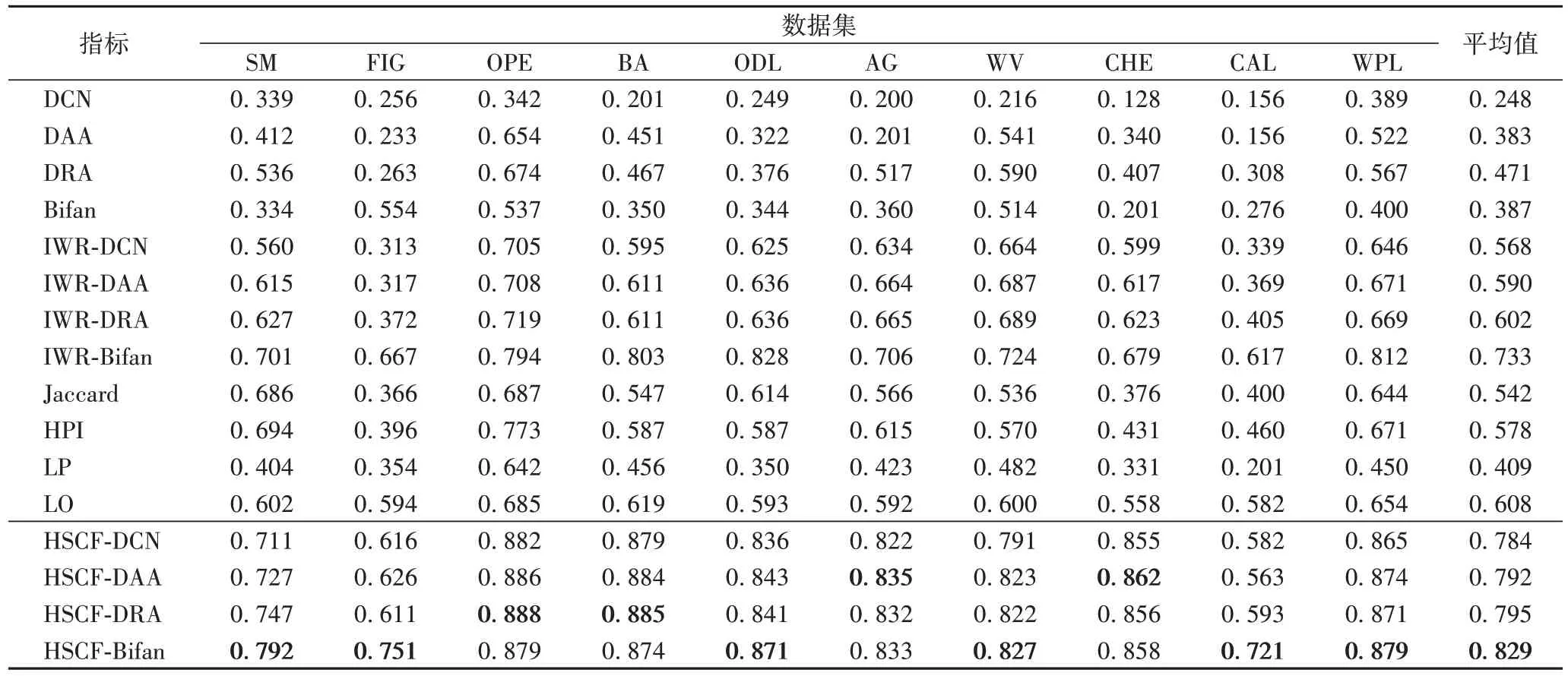
表3 不同指标下的F-score对比Tab.3 Comparison of F-score under difference indices

4）所提指标通过启用随机游走方法捕获节点三阶和四阶路径信息，捕获更多网络结构信息应对冷启动以及稀疏性问题。例如在数据集CAL中，稀疏率达到0.000 2，意味着网络中存在大量的孤立节点，从实验结果来看，所提指标HSCF-Bifan的AUC达到0.996，综合指标F-score也达到最优，表明该指标可有效处理冷启动以及稀疏性问题。

实验二测试基准指标和本文所提指标鲁棒性，按一定比例随机划分原始网络，设训练集比率为0.3、0.5 和0.7。当训练集比率为0.3 时意味着测试集比率高达0.7，网络处于极度稀疏状态。实验结果记录在表4～5，可观察到以下两个现象：

1）从表4 可观察到所提4 个指标在所有数据集上在不同训练下性能优于基准指标，表明所提指标具有良好的鲁棒性。当训练集比率从0.7 降至0.3，各个指标的AUC也随之下降。尤其在数据集SM、PB、CAL 和WV中，所提指标在不同训练集下AUC波动不明显，其他指标如LO 和LP 出现显著的波动，表明所提指标在以上数据集捕获更多网络结构信息来弥补稀疏性不足。此外，当可训练集比率为0.7时，10 个有向网络处于极度稀疏状态，然而所提指标依然最优，尤其在数据集SM、PB、CAL 和WV中AUC和F-score保持不变，表明所提方法鲁棒于稀疏网络。

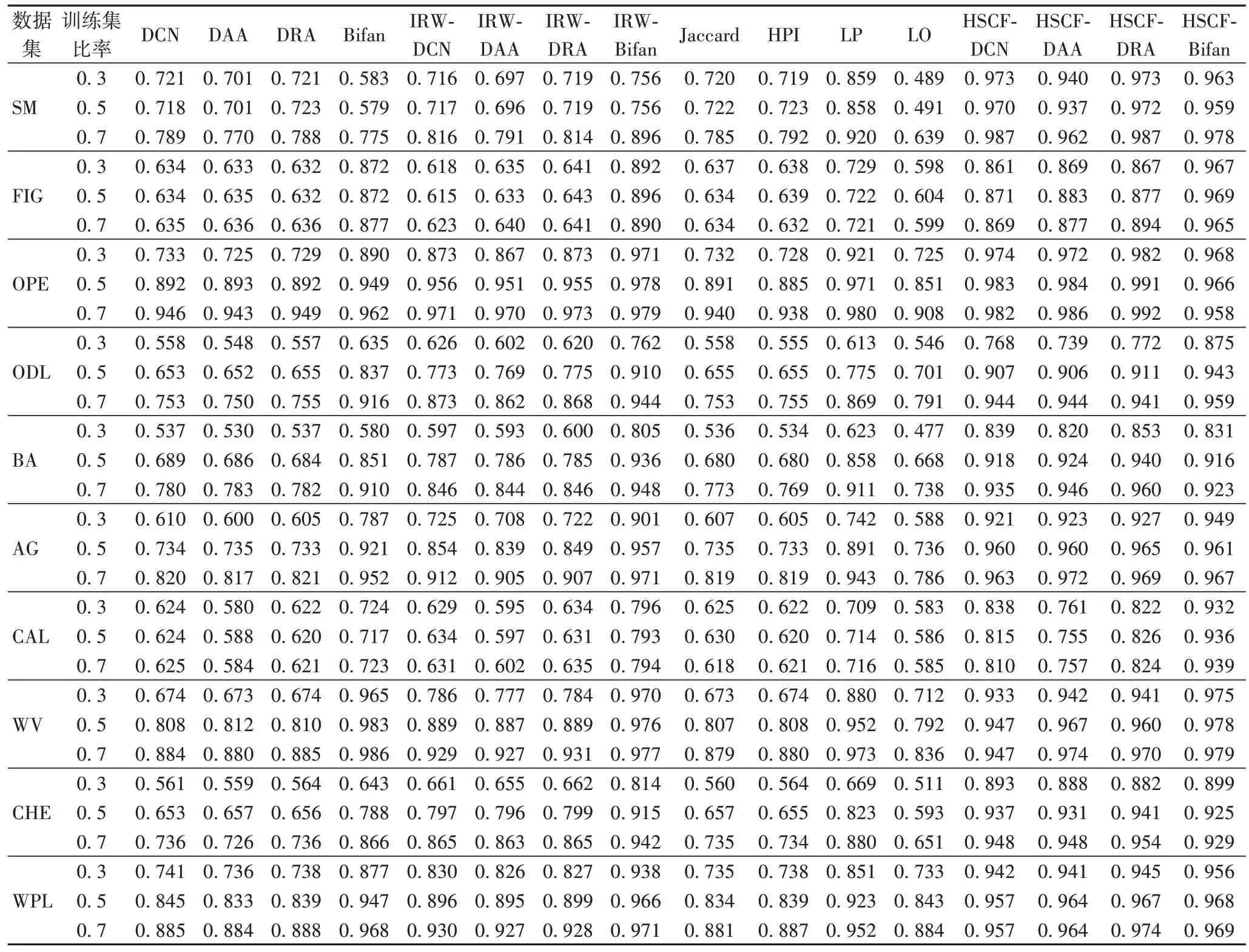
表4 不同训练集比率对应的AUCTab.4 AUC corresponding to different training dataset rate

2）从表5 可观察到所提指标在所有数据集上性能明显优于基准方法，表明所提指标同时保持局部和全局信息捕获更多网络结构信息弥补稀疏性。基于局部相似度（DCN、DAA 和DRA）性能最差，当可训练集比率增加时，F-score波动显著主要原因是无法捕获更多局部结构信息。LO 和IRW-Bifan 最接近本文指标，两个指标本质是考虑三阶路径信息可获得更多网络结构信息。半局部指标LP 表现并不理想，原因是可观察链接减少时该指标无法捕获更多二阶和三阶路径信息。

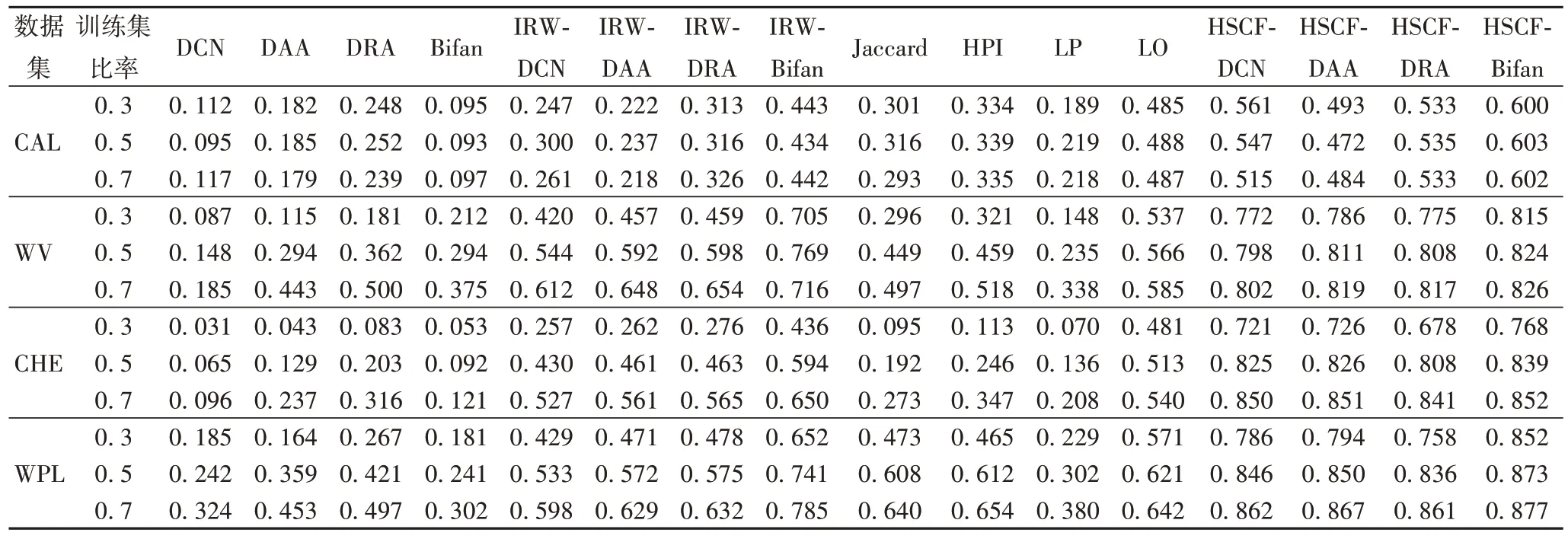
续表

实验三测试所提指标的运行时间，运行10 次的实验结果记录在图2 中。图2（a）是节点小于5 000 的有向网络，所提4 个指标耗时均小于250 s，表明所提指标适用于小型网络。图2（b）是节点数大于5 000，其中WPL 是大规模网络，HSCF-DRA 运行时间仅略高于500 s，HSCF-DCN 和HSCFDAA 略高于1 000 s，HSCF-Bifan 指标最为耗时。然而在CAL数据集中（节点数为9 664），本文指标均小于500 s。综上所述，所提指标可适用于大中规模网络。

最后，进行可调参数敏感性分析。由于0.1 ≤α≤0.9，实验中设α为0.1、0.3、0.5、0.7 和0.9，其实验结果 见图3～4。α的作用是平衡三阶和四阶路径信息的贡献。图3是不同α所对应的AUC，可观察到在数据集SM、ODL、WPL、AG、CAL 和WV中，α=0.1时AUC最优即算法性能最佳，随着α增加，AUC随着下降，表明所提指标在α=0.1 时可捕获更多网络结构信息。而在数据集BA中，当α=0.5时AUC获得最优。在数据集FIG中，观察到当α=0.3时，HSCF-DCN、HSCFDAA 和HSCF-DRA 三个指标AUC最优；而当α=0.1 时HSCFBifan 指标的AUC 值最佳。

图4 中不同α对应F-score值，F-score是综合全面评估度量。同理与AUC一致，当α=0.1时，数据集SM、FIG、ODL、WPL、CHE、AG、CAL 和WV 对应的F-score值最优；α=0.5时，数据集OPE 对应的F-score值最优，表明所提指标具有良好的稳定性。在数据集BA中，观察到当α=0.3时，HSCF-DAA、HSCF-DRA 和HSCF-BifanHSCF-Bifan 的性能最优；当α=0.1时，HSCF-DCN 指标F-score值最优。

3 结语

大部分现存的链路预测方法仅关注无向无权网络忽略有向网络方向链接和有向结构，难以同时保持有向网络局部和全局结构信息是个挑战问题，为此，本文提出高阶自包含协同过滤链路预测指标，该指标可以在保持局部结构信息基础上捕获更多全局结构信息。首先启用随机游走方法计算高阶相似度，再将三阶和四阶相似度矩阵融合协同过滤框架构建高阶自包含协同过滤预测框架，并将DCN、DAA、DRA和Bifan 四个指标融合以上框架构建有向网络链路预测指标。在10 个真实世界有向网络上与基准指标比较，结果表明所提指标性能优于基准指标。

在将来工作中，尝试将有向网络社区结构融合本文框架中，有助于理解有向网络的演化规律。此外，进一步优化该框架处理加权网络链路预测问题。